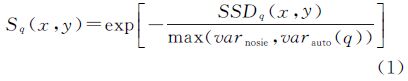2. 武汉大学 遥感信息工程学院,湖北 武汉 430079;
3. 美国普渡大学 土木工程学院,西拉法叶 47907;
4. 中国科学院 电子学研究所,北京 100190
2. School of Remote Sensing and Information Engineering,Wuhan University,Wuhan 430079,China;
3. School of Civil Engineering,Purdue University,West Lafayette,IN 47907,USA;
4. Institute of Electronics,Chinese Academy of Sciences,Beijing,100190
1 引 言
随着航空、航天技术的飞速发展,数据获取手段的不断丰富,如何充分集成多传感器、多光谱数据,对其进行综合处理,已成为现阶段亟待解决的问题之一。多光谱遥感图像通常包含了地物的不同特性,能够为地表监测提供互补的信息。为了整合这些图像进行对地观测,需要在地理空间上对它们进行几何配准。由于地物在不同波谱下的辐射特性有所不同,多光谱遥感图像间往往存在较大的灰度差异,尤其在可见光和红外图像之间[1],这些差异导致了在图像间识别同名点非常困难。因此,多光谱遥感图像的自动配准是目前研究的难点之一。
目前大多数的图像配准方法通常可分为两类:基于特征的方法和基于区域的方法[2]。基于特征的方法首先在图像间提取特征,然后利用特征间的相似性进行匹配。常用的基于特征的方法包括了基于点特征的方法[3]、基于线特征的方法[4]和基于面特征的方法[5]。最近,具有旋转和尺度不变性的尺度不变特征变换(scale invariant feature transform,SIFT)也被广泛地应用于遥感图像的配准[6, 7]。这些方法通常要求在图像间检测到的特征具有较高重复率,不过当图像间灰度差异较大时,特征检测的重复率往往较低[8],因此难以使用上述方法对多光谱遥感图像进行自动配准。
基于区域的方法可以被认为是一种模板匹配的方法[9]。该方法首先在参考图像上定义一个模板窗口,然后以某种相似性测度为准则,在待配准图像上寻找对应的模板区域,最后选择模板的中心点作为匹配点。常用的相似性测度包括了归一化相关系数(normalized correlation coefficient,NCC)、相位相关和互信息(mutual information,MI)等。作为一种经典的相似性测度,NCC已经被广泛地应用于遥感图像的配准。但是NCC对于灰度只具有线性不变性,不能很好地适用于图像间灰度差异较大的情况,尤其是非线性的灰度差异[10]。MI能够比较有效地抵抗图像间的灰度差异,已经被成功地应用于多传感器、多光谱遥感图像的配准[2, 11],但是基于MI的配准方法计算量较大[10],限制了它在遥感图像配准中的广泛应用。
尽管多光谱遥感图像间具有较大的灰度和纹理差异,但影像间轮廓和局部形状具有较高的相似性。针对这一特性,本文把局部自相似(local self-similarity,LSS)引入到多光谱图像的配准中。LSS是一种反映图像内在几何布局和局部形状属性的特征描述子[12],它已经应用于图像分类[13]、目标识别[14]以及多模态视频数据配准[15]等领域。本文将基于LSS构建一种形状相似性测度,并采用模板匹配的策略对多光谱遥感影像进行配准。根据遥感图像的特点,设计一种基于LSCC的自动配准方法,并选用不同传感器的多光谱遥感图像作为试验数据对该方法进行验证。
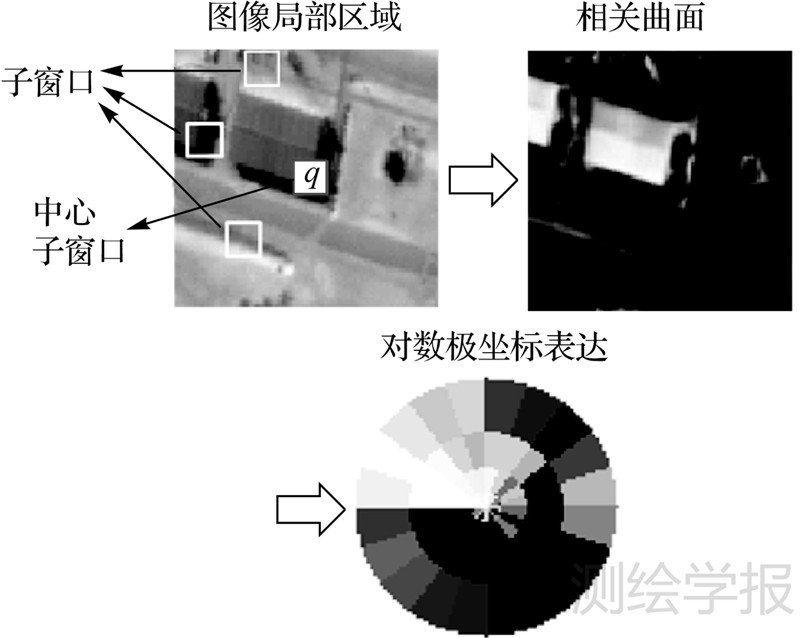
2 基于LSS的相似性测度LSS是一种描述图像内在几何布局的特征算子,它反映了图像局部区域的形状属性。根据这一性质,LSS能够匹配纹理或者灰度差异较大的图像,只要图像间具有相似的几何布局和形状特征[12]。图 1为一幅图像局部区域的LSS描述子的形成过程。
|
| 图 1 LSS描述子的形成过程 Fig. 1 An example of LSS descriptor generation |
在局部区域中,以每个像素为中心取一定大小的邻域(3像素×3像素)作为子窗口,并计算所有的子窗口与中心子窗口的灰度差方和(sum of square differences,SSD),然后利用式(1)对SSD进行归一化处理转化为“相关曲面”Sq(x,y)
式中,varnoise是一个常数,表示由光照和噪声等引起的灰度变化;varauto(q)用来顾及子窗口的对比度以及相应的模式结构,当模式改变时,边界区域比灰度平坦区具有更好的容忍度。在实际应用中,varauto(q)为中心子窗口与其邻域(半径为1)内子窗口间的SSD最大值。为了使描述子对于局部仿射形变具有一定的容忍性,把相关曲面Sq(x,y)转化到对数极坐标下,并在角度和径向方向上分别划分20份和4份,形成80个子区域。在每个子区域里,选择最大的“相关值”作为特征值,形成80维的LSS描述子。最后对LSS描述子进行归一化处理,进一步消除灰度变化造成的影响。图 2显示了同一场景下的可见光和红外图像的角点、边界和平坦区域的LSS描述子。可以看出,虽然两幅图像之间存在着较大的灰度差异,但它们的LSS描述子却十分相似。

|
| 图 2 可见光图像和红外图像的LSS描述子 Fig. 2 The LSS descriptors of the visible and infrared images |
由于多光谱图像间的局部形状具有较高的相似性,所以本文采用LSS描述子间的NCC(称为LSCC)作为匹配的相似性测度。LSCC表示图像间的形状相似性,其定义如下
式中,SqA和SqB分别代表图像A和B的LSS描述子;SqA和SqB分别代表图像A和B的LSS描述子的平均值;n表示LSS描述子的维数。 3 LSCC、NCC和MI匹配性能对比为了验证LSCC的优势和可行性,本文采用模板匹配的策略,通过相似性曲线、匹配正确率和计算效率3个方面与NCC和MI进行结果对比和详细分析。
3.1 相似性曲线相似性曲线是定性分析相似性测度匹配能力的一个重要指标[16]。通常情况下,当图像处于正确匹配位置时,相似性曲线刚好处于最大值(或最小值)的位置。这里使用的试验数据是一组可见光和红外图像,如图 3所示。可以看出,两幅图像间灰度差异较大,并且还出现了灰度反转的情况。图中实线框表示模板窗口,虚线框表示搜索区域,其范围为X轴方向的-20像素到20像素。为了分析模板尺寸对匹配性能的影响,这里采用两组不同尺寸的模板,大小分别为21像素×21像素和51像素×51像素。两组图像是完全配准的数据,因此当相似性曲线位于“0”时,模板刚好处于正确的匹配位置。

|
| 图 3 测试相似性曲线的图像 Fig. 3 Images for testing the similarity curve |
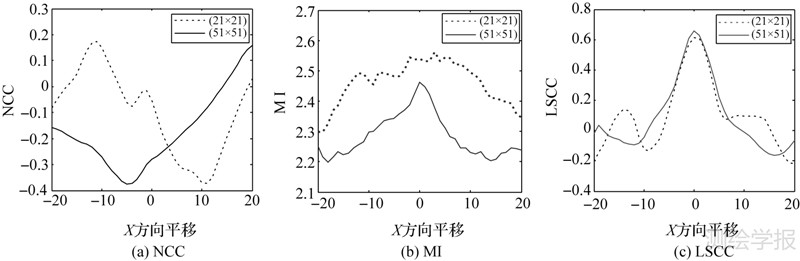
图 4显示了NCC、MI和LSCC 3种相似性测度的曲线。从图 4(a)可以看出,不管是大模板窗口还是小模板窗口,NCC都不能得到正确的匹配。对于MI(图 4(b)),当模板较大时,其相似性曲线的最大值刚好位于正确的位置,但是在模板较小的情况下,MI则不能进行有效的匹配。而LSCC在不同尺寸的模板情况下都获得了正确的匹配,如图 4(c)所示。以上结果初步说明了LSCC是一种相对比较稳健的相似性测度,受模板尺寸影响较小。
|
| 图 4 NCC、MI和LSCC的相似性曲线< Fig. 4 Similarity curves of NCC,MI,and LSCC |
上一节利用相似性曲线对NCC、MI和LSCC的匹配性能进行了定性的分析。本节将从匹配正确率和计算效率两方面对它们进行定量的分析和比较。这里选择4组多光谱遥感图像作为试验数据,其数据描述如表 1所示。4组数据都是由可见光和红外图像组成,波谱类型的不同造成了图像间存在着显著的非线性灰度差异(图 5)。为了避免时相差异对匹配的影响,每组的参考图像和待配准图像都是同一时间段获取的数据。试验平台采用主频为Inter Core 3.20GHz,内存2GB,运行环境为Window XP的计算机,编程语言为C++。
| 试验编号 | 参考图像 | 待配准图像 | 图像特点 | |||
| 传感器波长/μm | 大小/像素分辨率/m | 传感器波长/μm | 大小/像素分辨率/m | |||
| 试验1 | Daedalus波段2 0.52~0.60(绿) | 512×512 0.5 | Daedalus波段9 3.00~5.40(红外) | 512×512 0.5 | 位于居民区,结构和边缘特征清晰 | |
| 试验2 | Aster波段1 0.52~0.60(绿) | 855×860 15(采样为30) | ETM+波段4 0.76~0.90(近红外) | 855×860 30 | 位于城市郊区,结构和边缘特征比较清晰 | |
| 试验3 | ETM+波段3 0.63~0.68(红) | 530×506 30 | ETM+波段5 1.55~1.57(红外) | 530×506 30 | 位于郊外地区,结构和边缘特征比较清晰 | |
| 试验4 | TM波段1 0.45-0.52(蓝) | 832×872 30 | TM波段4 0.76~0.90(近红外) | 832×872 30 | 位于郊外地区,结构和边缘不够清晰,尤其是参考图像 | |

|
| 图 5 4组试验的参考图像(左)和待配准图像(右) Fig. 5 The reference (left) and sensed images (right) in the four tests |
首先利用Harris算子在参考图像上提取300个分布均匀的特征点,然后在待配准图像的X轴和Y轴方向上确定[-20,20]的搜索区域,并采用不同尺寸的模板窗口进行匹配(尺寸范围从21像素×21像素到101像素×101像素,以10像素×10像素为步长逐渐增加),同时利用匹配点3×3邻域内像素的LSCC值进行二元二次多项式拟合,求解出极值点的位置,即获得子像素精度[9],最后把误差在1.5个像素内的匹配点视为正确的匹配。为了便于匹配点误差统计,4组试验图像都事先经过配准,并采样为同样的分辨率,因此当匹配点位于正确位置时,它们的坐标应该完全相同。
图 6显示了3种相似性测度的匹配正确率。可以看出,对于4组试验数据,LSCC的匹配正确率明显高于NCC,这是因为NCC对于图像间的灰度只具有线性不变性,当灰度差异较大,尤其是非线性的灰度差异时,NCC通常不能得到满意的匹配效果[10]。LSCC和MI的匹配正确率都随着模板尺寸的增加而提高,并在模板较大时趋于稳定。但是MI的匹配正确率对于模板尺寸的变化更为敏感,当模板较小时,其匹配正确率较低,甚至低于NCC。这说明了MI的匹配性能很大程度上依赖于模板尺寸。因为在计算MI时,需要统计两幅图像的联合熵,而联合熵对于样本数量(即模板尺寸)非常敏感[10]。与MI相比,LSCC的匹配正确率相对于模板尺寸的变化更加稳定,即使当模板较小时,LSCC也能取得较好的匹配结果。

|
| 图 6 4组试验中NCC、MI和LSCC的匹配正确率 Fig. 6 Correct matching rates of NCC,MI and LSCC for the four tests |
另外,由于试验图像类型的不同,LSCC和MI的匹配正确率有所变化。在前3组试验中,当模板较小时,LSCC的匹配正确率要明显高于MI,在模板较大的情况下,LSCC和MI的匹配正确率几乎趋近于一致,达到了90%左右。而对于试验4,LSCC的匹配正确率有所下降,并且当模板尺寸增加到61像素×61像素时,LSCC的匹配正确率开始略低于MI。主要原因是由于试验4中参考图像的结构和边缘不够清晰,而LSCC依赖于描述形状特征的LSS算子,当图像间边缘信息不够丰富时,LSS算子的性能会有所下降。尽管如此,当模板窗口足够大时,LSCC匹配正确率也达到了70%左右(图 6(d))。
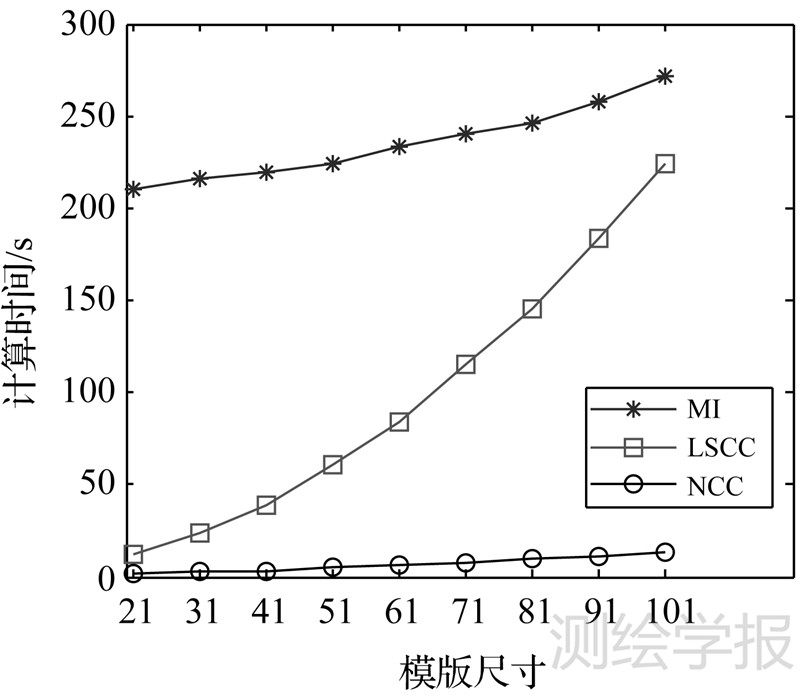
图 7显示了以上试验所耗费的匹配时间。可以看出,MI耗时相对较多。这是因为MI需要统计模板图像间的联合直方图,其计算量较大[10]。另一方面,LSCC的计算时间随着模板窗口的变大增长得相对较快。主要原因在于LSCC需要统计子窗口和中心窗口间的SSD,当模板增大时,其计算量增加的幅度相对较大。尽管如此,在所采用的模板尺寸范围内(小于101像素×101像素),LSS的计算效率要高于MI,这对于实际应用是非常有益的。因为大模板窗口会增加匹配的计算量,而且当模板窗口超过一定大小(大约81像素×81像素)时,LSCC和MI的匹配正确率并没有显著提高(图 6)。因此,综合考虑匹配正确率和计算效率,LSCC是一个相对较好的选择。
|
| 图 7 NCC、MI和LSCC的计算时间 Fig. 7 Computation time of NCC,MI and LSCC |
通过以上分析可知,LSCC的匹配性能比较稳健,并且对图像间的灰度差异不敏感。因此,本文根据遥感图像的特点,设计了一种基于LSCC的自动配准方法。
4.1 方法步骤配准的方法步骤如下:
(1) 利用卫星图像的地理坐标信息或者RPC参数对其进行粗纠正,消除图像间的旋转和尺度差异,使图像间仅存在一定量(几十个像素以内,与卫星性能有关)的平移关系[17, 18]。
(2) 使用Harris算子,采用分块的策略,在参考图像上提取大量的、分布均匀的特征点。
(3) 在待配准图像上预测一定大小的搜索区域,以LSCC作为匹配测度,并构建图像金字塔进行逐层匹配,同时使用双向的匹配策略[19]消除一些不确定的同名点。
(4) 对同名点进行三次多项式拟合,计算同名点的残差和均方根误差(root mean square error,RMSE),并迭代地剔除残差较大的同名点,直到RMSE小于某一阈值(如1个像素)。
(5) 采用三角网小面元模型对待配准图像进行纠正,以消除由于地形起伏造成的局部形变。
4.2 试验结果为了验证本文方法的有效性,采用两组来自不同传感器的多光谱遥感图像进行试验,其中一组数据是来自SPOT 4和TM传感器的中分辨率图像,位于武汉南部的郊外地区,另一组是来自Quickbird和SPOT 5传感器的高分辨率图像,位于武汉市城区,时相差异较大。数据的详细描述如表 2所示。
| 试验编号 | 参考图像 | 待配准图像 | |||||
| 传感器波长/μm | 大小/像素时间 | 分辨率/m | 传感器波长/μm | 大小/像素时间 | 分辨率/m | ||
| 试验1 | SPOT 4波段2 0.61~0.68(红) | 1475×1761 2002-09-15 | 20 | TM波段5 1.55~1.75(红外) | 973×1156 2003-09-11 | 30 | |
| 试验2 | Quick波段4 0.76~0.90(近红外) | 1158×1505 2005-08-02 | 2.4 | SPOT 5 全色波段0.51~0.73(全色) | 1180×1546 2002-10-10 | 2.5 | |
在试验中,参考图像分为10×10个子区域,在每个区域提取15个Harris特征点,总共为1500个特征点,建立3层金字塔影像,模板窗口为51像素×51像素。关于精度评定,手工地在参考图像和配准后的图像间选取20个检查点,并统计RMSE来表示配准精度。图 8和图 9分别显示了两组试验的同名点位图和配准结果,表 3列出了试验中获得的同名点数量和配准精度。

|
| 图 8 试验1的配准结果 Fig. 8 Registration result of test 1 |

|
| 图 9 试验2的配准结果 Fig. 9 Registration result of test 2 |
| 试验编号 | 匹配点 | 正确匹配点 | RMSE/像素 |
| 试验1 | 1095 | 850 | 0.68 |
| 试验2 | 784 | 553 | 1.22 |
可以看出,本文的方法成功地实现了两组试验数据的配准。不过由于数据类型的差异,所获得的同名点数量以及配准精度有所不同。在试验2中,参考图像和待配准图像有大概3a的时相差异,这期间某些区域已经发生了变化(如图 9的右上角),导致了图像间对应区域的减少,因此相比于试验1,获得了更少的同名点。另一方面,试验1的配准精度要高于试验2,这是因为试验2的数据是位于城市地区的高分辨率图像,建筑物的投影视差造成了图像间存在较大的局部形变。通过图像与图像之间的配准很难消除这类几何形变,只有使用真正射影像制作技术才能很好地解决这个问题[20]。
为了说明本文方法对于图像几何形变的适用性,对试验1中的输入图像分别进行旋转和缩放,再进行配准,其结果如表 4所示。
| 旋转角度(顺时针) | RMSE/像素 | 缩放倍数(放大) | RMSE/像素 |
| 5° | 1.03 | 1.2 | 1.55 |
| 15° | 2.14 | 1.4 | 3.09 |
| 30° | failed | 1.6 | failed |
| 注:“failed”指RMSE大于10个像素 | |||
从表 4可以看出,对于存在较小旋转和尺度差异的图像,本文方法能够成功配准,说明本文方法对于图像间的几何形变具有一定的适应能力。不过当图像间几何形变较大时,本文方法的适用性不强。这是由于较大的几何形变会导致图像间模板窗口内的像素内容不一致,从而使窗口内的LSS描述子无法对应所造成的。
5 结 论针对多光谱遥感图像间灰度差异较大所造成的配准问题,本文在反映图像内在几何布局和形状属性的LSS算子的基础上,构建了一种描述形状相似的匹配测度(LSCC)。为了验证LSCC的可行性和抗差性,将其与NCC和MI在匹配性能方面进行了详细的分析和对比,结果表明:LSCC的匹配正确率要明显高于NCC,综合考虑匹配正确率和计算效率时,相对于MI也具有一定的优势。另外,根据遥感图像的特点,设计了一种基于LSCC的自动配准方法。通过对两组来自不同传感器的多光谱图像进行试验,验证了该方法能够较好地抵抗图像间的非线性灰度差异,并获得了可靠的配准精度。
作为一种有效的匹配测度,LSCC可以应用到其他领域的图像匹配和配准中。需要注意的是,当图像的结构和形状信息不够丰富或者图像间存在较大几何形变时,LSCC的性能有所下降。因此,以后将针对这些问题进行深入研究,对LSCC进行优化和改进。
| [1] | KERN J P, PATTICHIS M S. Robust Multispectral Image Registration Using Mutual-information Models[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007,45(5): 1494-1505. |
| [2] | ZITOVA B,FLUSSER J. Image Registration Methods: A Survey[J]. Image and Vision Computing, 2003, 21(11): 977-1000. |
| [3] | ZHANG Dengrong,YU Le,CAI Zhigang. Matching Method Based on Harris Operator and Wavelet Pyramid[J]. Journal of Zhejiang University: Science Edition, 2007, 34(4): 465-468. (张登荣,愈乐,蔡志刚. 点特征和小波金字塔技术的遥感图像快速匹配技术[J]. 浙江大学学报: 理学版, 2007, 34(4): 465-468.) |
| [4] | SHI W, SHAKER A. The Line-based Transformation Model(LBTM) for Image-to-Image Registration of High-resolution Satellite Image Data[J]. International Journal of Remote Sensing,2006,27(14):3001-3012. |
| [5] | GONCALVES H,GONALVES J A,CORTE-REAL L. HAIRIS: A Method for Automatic Image Registration through Histogram-based Image Segmentation[J]. IEEE Transactions on Image Processing,2011,20(3):776-789. |
| [6] | LOWE D G. Distinctive Image Features from Scale Invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. |
| [7] | YANG Huachao,ZHANG Lei,YAO Guobiao,et al. An Automated Image Registration Method with High Accuracy Based on Local Homography Constraint[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 401-408. (杨化超, 张磊, 姚国标, 等. 局部单应约束的高精度图像自动配准方法[J]. 测绘学报, 2012, 41(3): 401-408.) |
| [8] | KELMAN A,SOFKA M,STEWART C V. Keypoint Descriptors for Matching across Multiple Image Modalities and Non-linear Intensity Variations[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Minneapolis: IEEE Press, 2007: 3257-3263. |
| [9] | MA J L, CHAN J C W, CANTERS F. Fully Automatic Subpixel Image Registration of Multiangle CHRIS/Proba Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(7): 2829-2839. |
| [10] | HEL-OR Y,HEL-OR H,DAVID E. Fast Template-matching in Non-Linear Tone-mapped Images[C]//Proceedings of IEEE International Conference on Computer Vision. New York: IEEE Press, 2011: 1355-1362. |
| [11] | COLE-RHODES A A, JOHNSON K L, LEMOIGNE J, et al. Multiresolution Registration of Remote Sensing Imagery by Optimization of Mutual Information Using a Stochastic Gradient[J]. IEEE Transactions on Image Processing, 2003, 12(12): 1495-1511. |
| [12] | SHECHTMAN E, IRANI M. Matching Local Self-similarities across Images and Videos[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE Press, 2007: 1-8. |
| [13] | YANG J, LI Y, TIAN Y, et al. Group-sensitive Multiple Kernel Learning for Object Categorization[C]//Proceedings of IEEE International Conference on Computer Vision. New York: IEEE Press, 2009: 436-443. |
| [14] | VEDALDI A, GULSHAN V, VARMA M, et al. Multiple Kernels for Object Detection[C]//Proceedings of IEEE International Conference on Computer Vision. New York: IEEE Press, 2009: 606-613. |
| [15] | TORABI A, BILODEAU G A. Local Self-similarity as a Dense Stereo Correspondence Measure for Themal-visible Video Registration[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops. New York: IEEE Press , 2011: 61-67. |
| [16] | MA Zhengde, DU Yunfei,ZHOU Haifang,et al. Performance Comparison of Similarity Measures Remote Sensing Image Registration[J]. Computer Engineering & Science,2008,30(2),45-48. (马政德,杜云飞,周海芳, 等. 遥感图像配准中相似性测度的比较[J]. 计算机工程与科学,2008, 30(2):45-48.) |
| [17] | YUE Chunyu,JIANG Wanshou. An Automatic Registration Algorithm for SAR and Optical Images Based on Geometry Constraint and Improved SIFT[J]. Acta Geodaetica et Cartographica Sinica,2012,41(4):570-576. (岳春雨,江万寿. 几何约束和改进SIFT的SAR影像和光学影像自动配准方法[J]. 测绘学报,2012,41(4):570-576.) |
| [18] | REINARTZ P, MVLLER R, SCHWIND P, et al. Orthorectification of VHR Optical Satellite Data Exploiting the Geometric Accuracy of TerraSAR-X Data[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2011, 66(1): 124-132. |
| [19] | YU L, ZHANG D R, HOLDEN E J. A Fast and Fully Automatic Registration Approach Based on Point Features for Multi-source Remote-sensing Images[J]. Computers & Geosciences, 2008, 34(7): 838-848. |
| [20] | HONG G, ZHANG Y. Wavelet-based Image Registration Technique for High-resolution Remote Sensing Images[J]. Computers & Geosciences, 2008, 34(12): 1708-1720. |