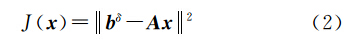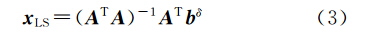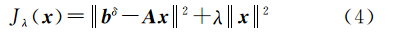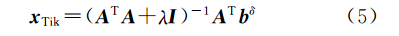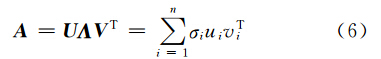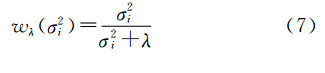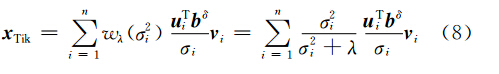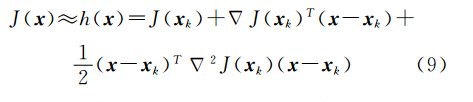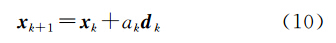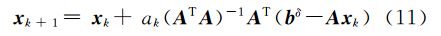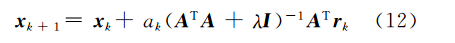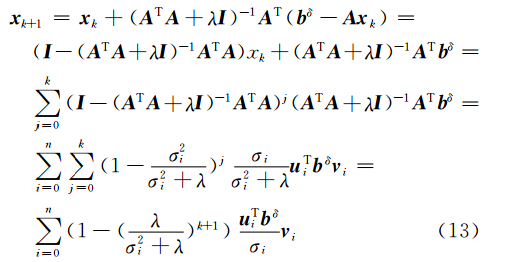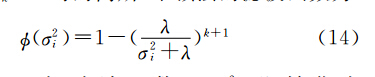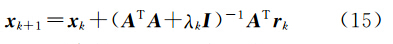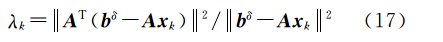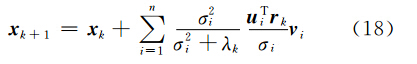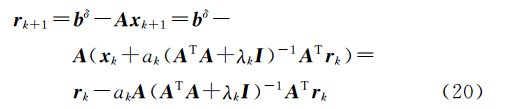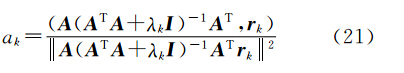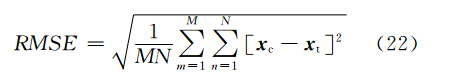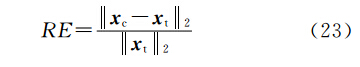1 引 言
位场向下延拓在地质勘探资料解析、磁性目标探测定位及重力场和地磁场辅助惯性导航基准图制备等很多方面都有十分重要的作用。位场向下延拓是一个典型的线性不适定反问题,对于该类问题的求解一般有两种策略[1]:一是正则化方法;二是迭代法。正则化方法方面,文献[2]给出了航空重力向下延拓的正则化算法,并对重力数据处理中常用的几种向下延拓方法进行了比较,得出正则向下延拓效果相对最好的结论;文献[3]依据信噪比构造正则化矩阵,以极小化均方误差为目标选取正则化参数构造正则化矩阵,提出基于信噪比的正则化方法;文献[4]提出将基于多个最优正则化参数的广义岭估计用于航空重力向下延拓,并通过对比试验说明,广义岭估计在可靠性、精度和稳定性方面均优于Tikhonov法和岭估计;文献[5]将系数矩阵相对较大和相对较小的奇异值区别对待,提出Tikhonov双参数正则化法并验证了该方法的有效性。迭代法方面,文献[6—7]提出了位场向下延拓的积分迭代法,相较传统的FFT法,该迭代法能够稳定向下延拓20倍点距,同时,有大量文献进行了相关研究[8, 9, 10, 11, 12, 13, 14, 15]。
本文首先将位场向下延拓视为一个线性优化问题,然后采用高斯-牛顿法来实现位场向下延拓。其次,基于奇异值分解定理,探讨了高斯-牛顿法的滤波函数及其滤波函数的滤波特性,并从滤波函数滤除高频噪声需要和目标函数最小化的角度,提出了改进算法。改进算法采用递增几何级数计算迭代法正则参数,并引入最优变步长策略来实现迭代法正则参数和迭代步长计算的完全自适应。最后,通过理论重力模型和实测航磁数据验证了改进迭代法的有效性。
2 位场正则向下延拓原理
位场向下延拓的数学模型可以简化为
式中,A为系数矩阵,并具有特殊结构[16];x为待求位场向下延拓数据;b为测量得到的已知位场数据,通常b不可避免地会带有一定的误差δ,即测量得到的数据为bδ,满足b-bδ≤δ。由于式(1)中即使A-1存在,也未必连续,造成方程(1)的求解很不稳定。此时,方程存在最小二乘意义下的解,即解应最小化如下的残差范数目标函数
由此得位场向下延拓的最小二乘解
位场向下延拓本质上是一个病态问题,延拓过程中会放大观测噪声。若采用最小二乘方法求解,即使较小的观测误差也会导致解的严重失真。一个解决该问题的有效途径是在目标函数中添加一个正则项。 Tikhonov正则化即是一种广泛应用的方法,它是指最小化如下目标函数
式中,λ为正则参数,用于平衡解的不稳定性及光滑性。式(4)的解为
对系数矩阵A作奇异值分解
式中,U=[u1 u2 … un]和V=[v1 v2 … vn]分别是A的左右奇异向量,且满足uiu T i =I,viv T i =I;Λ为对角矩阵,其对角元素由A的递减的奇异值σi组成。应用上述奇异值分解定理, Tikhonov正则解的滤波函数为
式(5)在频域内的形式为
3 位场改进高斯-牛顿法向下延拓原理
3.1 高斯-牛顿法基本原理
设xk是式(2)函数J(x)极小值的第k次近似,并将J(x)在xk处作二阶 Taylor展开,得
则由目标函数J(x)的 Hessian矩阵 Δ2J(x) =A T A的对阵正定性可知,J(x)的二次近似h(x)为正定二次函数,因此,h(x)为存在唯一全局极小值的凸函数。令 Δ h(x)=0,近似得 Δ J(xk)+ Δ2J(xk)(x-xk)=0,将此式的解作为J(x)极小值的第k+1次近似xk+1,即得高斯-牛顿法公式[17]
式中,dk=[ Δ2J(xk)]-1 Δ J(xk)为修正量;ak为迭代步长或称线性搜索参数。
将J(x)的梯度 Δ J(x) = A T (bδ-Ax)和 Hessian矩阵代入式(10)得迭代法的迭代式为
由于反问题的病态性,直接用高斯-牛顿法求解,解出的值依然很不稳定,效果很不理想。为解决这个问题,对于式(11),一般在A TA后面加上一个带参数的单位阵,以使其具有良好的正则性质,克服当A T A奇异时,算法收敛到一个非驻点的情况。改进后的迭代格式如下
式中,rk=bδ-Axk为残差。
对比式(12)和式(5)可知,高斯-牛顿法迭代得到的解xk+1,都是上一步迭代得到的解xk加上用 Tikhonov正则化方法处理残差rk后得到的值的ak倍(即ak(A TA+λI)-1A Trk)而得到的。每次迭代过程中,当正则参数选择合适, Tikhonov正则能够有效利用残差rk中有效信息进行迭代结果修正的同时,压制残差rk中的噪声(来自残差rk=bδ-Axk中的bδ)。因此,定性地讲,高斯-牛顿法能够获得比 Tikhonov正则法更加精确的解,同时注意到每次迭代计算都仅包含一次Tikhonov正则计算,因此相较Tikhonov正则法,该迭代法并没有增加过多的运算量。
值得注意的是,当步长ak=1,式(12)等价于迭代 Tikhonov法[18]、Levenberg-Marquardt法[19]或预处理Landweber迭代法[20]。
3.2 滤波函数对比分析
当ak=1时,运用数学归纳法和系数矩阵A的奇异值分解可得
可见,ak=1时的高斯-牛顿法的滤波函数为
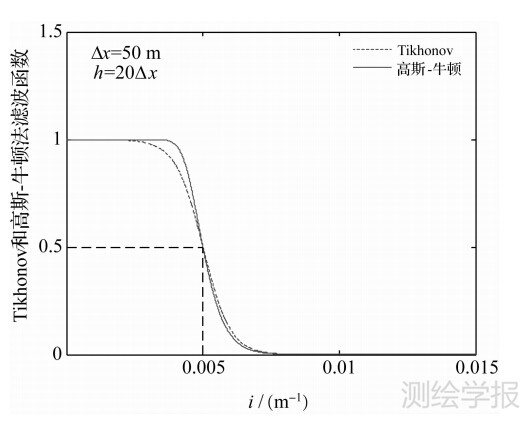
当k=0时,滤波函数 (σ2i)即转化为 Tikhonov正则滤波函数wλ(σ2i)。 (σ2i)和wλ(σ2i)的对比如图 1所示(以4.1节理论重力模型的相关参数为例)。其中,设滤波函数所形成的低通滤波器的截止频率为0.005(滤波函数的值降为0.5)。由图 1的比对可知,高斯-牛顿法滤波函数形成的滤波器的过渡带明显窄于(或称下降陡度明显大于) Tikhonov正则法,因此,从低通滤波器的滤波特性角度来讲,高斯-牛顿法的滤波函数优于Tikhonov正则法的滤波函数。
|
| 图 1 Tikhonov和高斯-牛顿法滤波函数特性的对比 Fig. 1 The characteristic comparison of filter functions for Tikhonov and Guass-Newton methods |
3.3 正则参数的选取
针对步长ak=1的情况,文献[21]进一步考虑了式(12)的非稳定隐式迭代形式
并相应采用正则参数选择的几何级数法
式中,λ0为正则参数初始设定值,且λ0>0,0
上述两种正则参数计算方法是伴随迭代的进行不断地更新,具有自适应的性质,且计算简单,因而具有相对较高的计算效率。但是,它们也存在严重的缺点,即存在严重的半收敛性:在迭代法迭代的过程中,伴随迭代次数的增加,向下延拓的误差先减后增。下面先定性分析其半收敛性产生的原因。
首先,将式(8)代入式(15)中可得迭代法非稳定隐式迭代形式在频域的形式
如3.1节的分析结论,迭代法每一步迭代得到的解xk+1都是上一步的迭代结果xk加上 Tikhonov正则处理残差rk后得到的值(即(A TA+αI)-1A Trk)而得到的。如此, Tikhonov正则的滤波函数wλ(σ2i)的滤波特性对结果影响很大。
同样以4.1节重力理论模型参数为例, Tikhonov正则的滤波函数wλ(σ2i)在不同正则参数λ条件下的变化如图 2所示。可见,wλ(σ2i)表现为一低通滤波,正则参数λ控制着该滤波函数的低通滤波特性:伴随正则参数λ的减小,其低通滤波的效果越来越不明显,即通过的高频信息会越来越多。由此,当用式(16)的几何级数法或式(17)的自适应法计算正则参数时,由于几何级数法中公比0 针对上述分析,本文相应提出如下的几何递增级数法用于正则参数的计算
式中,λ为 Tikhonov正则参数(通过广义交叉校验( GCV)准则[23]或 L-曲线法[24]求得),而该方法的关键在于选取合适的大于1的公比q。同时,为了确保迭代法在迭代过程中,对上一步得到的结果进行充分修正,根据 Tikhonov滤波函数的滤波特性分析,q不能过大,否则,λk的过快增长会使修正过程过快地结束而导致迭代法的最终结果改善有限,这在第四节的试验中可以看出。
3.4 残差最小步长准则
式(12)中迭代步长ak的选取显然也非常重要,过大可能导致迭代法发散,过小则影响迭代法的收敛速度,增加计算时间。一个简单而自然的想法是让步长ak的选取同样能够最小化迭代法中每一步的目标函数J(xk+1)=bδ-Axk+12。残差最小步长准则即由此而来[13]。
首先,设迭代法第k次迭代时的残差为rk=bδ-Axk,则其第k+1次迭代的残差
由J(xk+1)=bδ-Axk+12=rk+12,要使残差J(xk+1)最小,则令 dJ(xk+1) dak=0即可得残差最小最优步长
综上所述,本文改进高斯-牛顿法的具体实现步骤可描述如下:首先,令x0=0,以广义交叉校验( GCV)准则或L-曲线法(本文采用GCV准则)求得Tikhonov正则法的正则参数λ;然后,用式(19)即λk=λqk-1来计算迭代法的正则参数,且在每次迭代法计算过程中,采用由残差最小准则导出的步长计算公式(式(21))来更新迭代步长ak。从上面的描述可以看出,改进方法具有完全自适应的性质。下面的数值试验表明,改进迭代法的收敛速度较快,一般迭代10~20次左右就可以获得较好地收敛效果。
4 数值试验及结果比较
4.1 理论重力模型
采用文献[9]的双球体重力模型。两个球体的参数相同:剩余密度 Δσ=1.0 t/m3、半径r=0.5 km、中心埋深1.8 km、球心x坐标分别为10 km和15 km、球心y坐标12.5 km、z坐标向下为正,线数M和每线点数N同为512、点距 Δx和线距 Δy都为50 m。
试验中,以h=0 m平面处的重力数据为观测数据,并加入零均值、均方差为该高度理论重力异常绝对均值10 %的高斯白噪声以模拟实际情况,其结果如图 3所示。分别用 Tikhonov法和本文的改进高斯-牛顿法将加噪数据向下延拓1000 m(20倍点距),并用得到的延拓值x c与1000 m深度处的真实重力异常值x t采用均方误差 (root mean square error,RMSE)
和相关性误差( relative error,RE)
来计算、对比延拓误差[25],其结果如表 1(迭代法迭代次数k=10)和图 4(仅显示主剖面)所示。
本文迭代法的均方误差和相关性误差随公 比q和迭代次数的变化分别如图 5和图 6所示(迭代次数k=0对应Tikhonov 法)。从图 5和图 6中的对比可知,延拓误差随q的变化可大致分为3个阶段:当公比q≤1时,迭代法存在非常显著的半收敛性,即延拓误差随迭代次数的增加先减小,然后迅速增加;当公比1
4.2 航磁数据试验
航磁实测数据点距和线距均为250 m,其等值线图见图 7。将原始数据向上延拓5000 m(20倍点距)以构建另一个平面的数据。同时,考虑到向上延拓具有的平滑效应,为模拟实际情况,本文在向上延拓后得到的磁场数据中加入零均值、均方差为该延拓航磁数据绝对均值1%的高斯白噪声,加噪后航磁数据等值线图如图 8所示。与模型对比试验一样,分别采用Tikhonov法和本文方法分别将加噪向上延拓数据向下延拓20倍点距到原来的数据平面,并将得到的延拓值 xc 与原高度处的真实航磁异常值xt 进行比较,两种方法产生的均方误差和相关性误差对比如表 2所示(迭代法迭代次数 k=20)。
两种方法的延拓结果分别如图 9(Tikhonov法)和图 10(本文方法)所示。本文迭代法延拓的均方误差和相关性误差随迭代次数的变化分别如图 11和图 12所示(迭代次数 k=0对应Tikhonov法)。综合图 9~图 12分析可知:① 本文的改进迭代法向下延拓的过程稳定,且相较Tikhonov法,改进迭代法的延拓结果具有更小的延拓误差、带有更多的细节;② 选择公比1< q≤2既可以确保迭代法延拓结果的收敛性,又可以保证迭代法的结果得到最好的修正。
位场高精度稳定向下延拓方法的研究一直是其诸多相关应用领域的研究热点。本文提出一种基于递增几何级数自适应选择正则参数和残差最小步长准则的改进高斯-牛顿法用于位场向下延拓,并给出了迭代法的具体实现步骤。将改进方法应用到理论重力模型和实测航磁数据的向下延拓试验中,结果表明,改进迭代法能够有效地克服原迭代法的半收敛性,同时,相对传统的Tikhonov正则法具有更高的延拓精度。
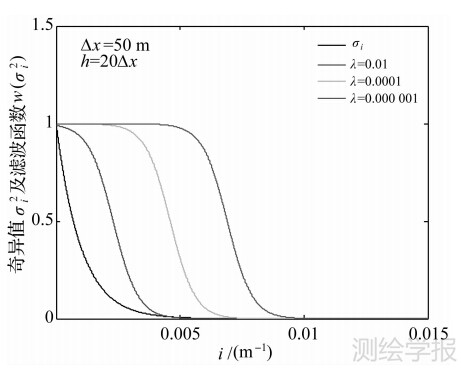
图 2 奇异值σ2i和 Tikhonov滤波函数wλ(σ2i)
Fig. 2 The singular value σ2i and the filter function wλ(σ2i) for Tikhonov method
1 mGal=1×10-5m/s正则参数 RMSE/mGal RE/(%)
Tikhonov 0.000 4 0.033 1 9.62
本文方法 0.000 4×1.8 k-1 0.026 2 4.85
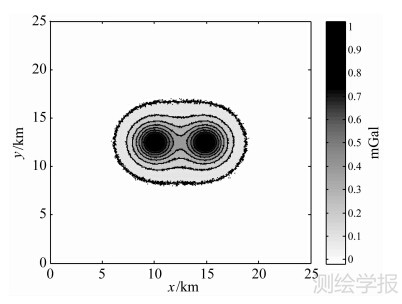
图 3 加噪重力异常等值线图
Fig. 3 Contours of the gravity anomaly data with noise
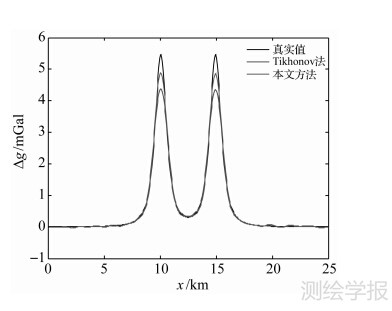
图 4 延拓结果在主剖面的对比
Fig. 4 The comparison of downward continuation results in main profile

图 5 延拓均方误差随公比 q和迭代次数的变化
Fig. 5 Relationship between root mean square errors and iteration numbers for the method in this paper
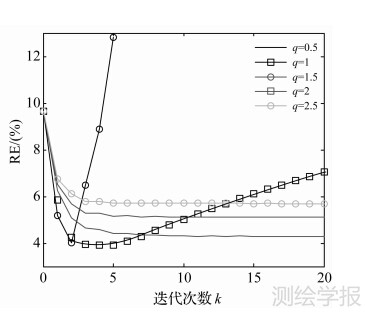
图 6 延拓相关性误差随公比 q迭代次数的变化
Fig. 6 Relationship between relative errors and iteration numbers for the method in this paper
正则参数 RMSE/nT RE/(%)
Tikhonov 0.000 5 12.59 8.38
本文方法 0.000 5×1.2 k-1 11.21 7.19
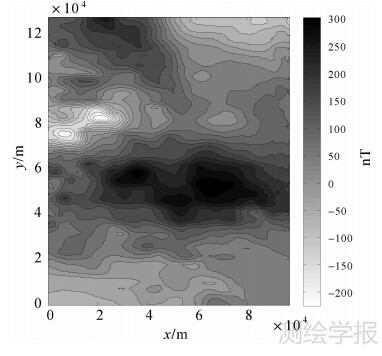
图 7 原始航磁等值线
Fig. 7 Contours of the original aeromagnetic field
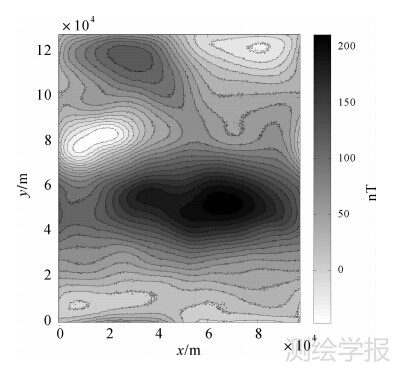
图 8 向上延拓航磁异常加噪等值线
Fig. 8 Contours of upward continuation of aeromagnetic field with noise
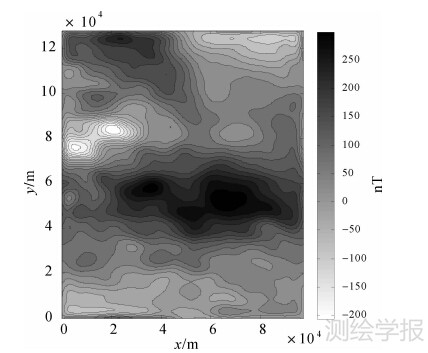
图 9 Tikhonov法向下延拓结果等值线
Fig. 9 Contours of the downward continued data for Tikhonov regularization method
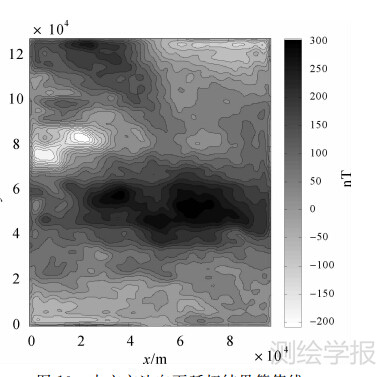
图 10 本文方法向下延拓结果等值线
Fig. 10 Contours of the downward continued data for the method in this paper
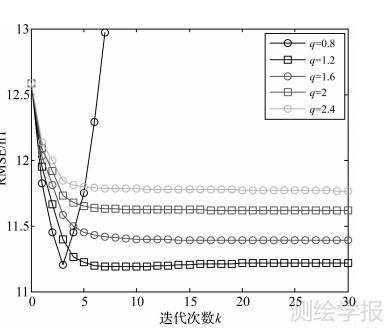
图 11 本文方法均方误差随迭代次数的变化
Fig. 11 Relationship between root mean square errors and iteration numbers for the method in this paper
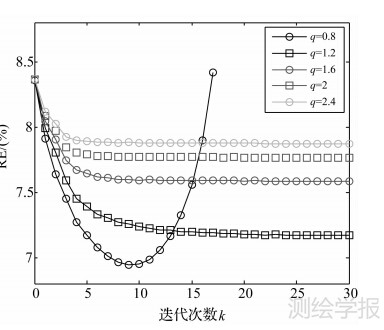
图 12 本文方法相关性误差随迭代次数的变化
Fig. 12 Relationship between relative errors and iteration numbers for the method in this paper
| [1] | WANG Yanfei. Computational Methods for Inverse Problems and Their Applications[M]. Beijing: Higher Education Press, 2007. (王彦飞. 反演问题的计算方法及其应用[M]. 北京: 高等教育出版社, 2007.) |
| [2] | WANG Xintao, SHI Pan, ZHU Feizhou. Regularization Methods and Spectral Decomposition for the Downward Continuation of Airborne Gravity Data[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(1): 33-38. (王兴涛, 石磐, 朱非洲. 航空重力测量数据向下延拓的正则化算法及谱分析[J]. 测绘学报, 2004, 33(1): 33-38.) |
| [3] | GU Yongwei, GUI Qingming. Study of Regularization Based on Signal-to-noise Index in Airborne Gravity Downward to the Earth Surface[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 458-464. (顾勇为, 归庆明. 航空重力测量数据向下延拓基于信噪比的正则化方法的研究[J]. 测绘学报, 2010, 39(5): 458-464.测绘学报, 2010, 39(5): 458-464.) |
| [4] | JIANG Tao, LI Jiancheng, WANG Zhengtao, et al. Solution of Ill-posed Problem in Downward Continuation of Airborne Gravity[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 684-689. (蒋涛, 李建成, 王正涛, 等. 航空重力向下延拓病态问题的求解[J]. 测绘学报, 2011, 40(6): 684-689.) |
| [5] | DENG Kailiang, HUANG Motao, BAO Jingyang, et al. Tikhonov Two-parameter Regulation Algorithm in Downward Continuation of Airborne Gravity Data[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 690-696. (邓凯亮, 黄谟涛, 暴景阳, 等. 向下延拓航空重力数据的Tikhonov双参数正则化法[J]. 测绘学报, 2011, 40(6): 690-696.) |
| [6] | XU Shizhe. The Integral-iteration Method for Continuation of Potential Field[J]. Chinese Journal of Geophysics, 2006, 49(4): 1176-1182 (徐世浙. 位场延拓的积分-迭代法[J]. 地球物理学报, 2006, 49(4): 1176-1182.) |
| [7] | XU S Z, YANG J Y, YANG C F, et al. The Iteration Method for Downward Continuation of a Potential Field from a Horizontal Plane[J]. Geophsical Prospecting, 2007, 55(6), 883-889. |
| [8] | ZHANG Hui, CHENG Longwei, REN Zhixin, et al. Analysis on Convergence of Iteration Method for Potential Fields Downward Continuation and Research on Robust Downward Continuation Method[J]. Chinese Journal of Geophysics. 2009, 52(4): 1107-1113. (张辉, 陈龙伟, 任治新, 等. 位场向下延拓迭代法收敛性分析及稳健向下延拓方法研究[J]. 地球物理学报, 2009, 52(4): 1107-1113.) |
| [9] | LIU Dongjia, HONG Tianqiu, JIA Zhihai, et al. Wave Number Domain Iteration Method for Downward of Potential Fields and Its Convergence[J]. Chinese Journal of Geophysics. 2009, 52(6): 1599-1605. (刘东甲, 洪天求, 贾志海, 等. 位场向下延拓的波数域迭代法及其收敛性[J]. 地球物理学报, 2009, 52(6): 1600-1605.) |
| [10] | YU Bo, ZHAI Guojun, LIU Yanchun, et al. The Downward Continuation Method of Aeromagnetic Data to the Sea Level[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(3): 202-209. (于波, 翟国君, 刘雁春, 等. 利用航磁数据向下延拓得到海面磁场的方法[J]. 测绘学报, 2009, 38(3): 202-209.) |
| [11] | YU Bo, ZHAI Guojun, LIU Yanchun, et al. Analysis of Noise Effect on the Calculation Error of Downward Continuation with Iteration Method[J]. Chinese Journal of Geophysics, 2009, 52(8): 2182-2188. (于波, 翟国君, 刘雁春, 等. 噪声对向下延拓迭代法的计算误差影响分析[J]. 地球物理学报, 2009, 52(8): 2182-2188.) |
| [12] | ZENG Xiaoniu, LI Xihai, HAN Shaoqing, et al. A Comparison of Three Iteration Methods for Downward Continuation of Potential Fields[J]. Progress in Geophysics. 2011, 26(3): 908-915. (曾小牛, 李夕海, 韩绍卿, 等. 位场向下延拓三种迭代方法之比较[J]. 地球物理学进展, 2011, 26(3): 908-915.) |
| [13] | ZENG Xiaoniu, LI Xihai, LIU Daizhi, et al. Regularization Analysis of Integral-iteration Method and the Choice of Its Optimal Step-length[J]. Chinese Journal of Geophysics, 2011, 54(11): 2943-2950. (曾小牛, 李夕海, 刘代志, 等. 积分迭代法的正则性分析及其最优步长的选择[J]. 地球物理学报, 2011, 54(11): 2943-2950.) |
| [14] | YAO Changli, LI Hongwei, Zheng Yuanman et al. Research on Iteration Method Using in Potential Field Transformations[J]. Chinese Journal of Geophysics, 2012, 55(6): 2062-2078. (姚长利, 李宏伟, 郑元满, 等. 重磁位场转换计算中迭代法的综合分析与研究[J]. 地球物理学报, 2012, 55(6): 2062-2078.) |
| [15] | GAO Yuwen, LUO Yao. WEN Wu. The Compensation Method for Downward Continuation of Potential Field from Horizontal Plane and Its Application[J]. Chinese Journal of Geophysics, 2012, 55(8): 2717-2756. (高玉文, 骆遥, 文武. 补偿向下延拓方法研究及应用[J]. 地球物理学报, 2012, 55 (8): 2747-2756.) |
| [16] | CHEN Longwei, HU Xiaoping, WU Meiping, et al. Research on Spatial Domain Continuation Method for Potential Field[J]. Progress in Geophysics, 2012, 27(4): 1509-1518. (陈龙伟, 胡小平, 吴美平, 等. 空间域位场延拓新方法研究[J]. 地球物理学进展. 2012, 27(4): 1509-1518.) |
| [17] | YUAN Yaxiang, SUN Wenyu. Optimization Theory and Methods[M]. Beijing: Science Press, 1997. (袁亚湘, 孙文瑜. 最优化理论与方法[M]. 北京: 科学出版社, 1997.) |
| [18] | KING J T, CHILLINGWORTH D. Approximation Generalized Inverse by Iterated Regularization[J]. Numerical Function Analysis and Optimization. 1979, 1(5): 499-513. |
| [19] | RANGANATHAN A. The Levenberg-Marquardt Algorithm[EB/OL]. 2004[2012-03-08]. http://www. ananth.in/ Notes_files/lmtut.pdf, 2004. |
| [20] | PIANA M, BERTERO M. Projected Landweber Method and Preconditioning[J]. Inverse Problems, 1997, 13(2), 441-464. |
| [21] | HANKE M, GROETSCH C W. Nonstationary Iterated Tikhonov Regularization[J]. Journal of Optimization Theory and Applications, 1998, 98(1): 37-53. |
| [22] | PEREVERZEV S V, SCHOCK E. pakhage’s Implicit Iteration Method and the Information Complexity of Equations with Operators Having Closed Range[J]. Journal of Complexity, 1999, 15(3): 385-401. |
| [23] | GOLUB G H, HEATH M, WAHBA G. Generalized Cross-validation as a Method for Choosing a Good Ridge Parameter[J]. Technometrics, 1979, 21(2): 215-223. |
| [24] | HANSEN P C, O'LEARY D P. The Use of the L-curve in the Regularization of Discrete Ill-posed Problems[J]. SIAM Journal on Scientific Computing, 1993, 14(6): 1487-1503. |
| [25] | ZHOU J, SHI G G, GE Z L. Study of Iterative Regularization Methods for Potential Field Downward Continuation in Geophysical Navigation[J]. Journal of Astronautics, 2011, 32(4): 787-794. |