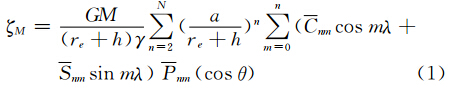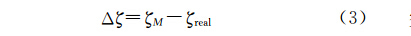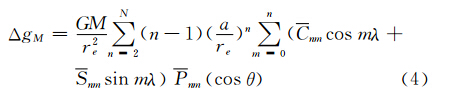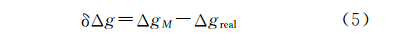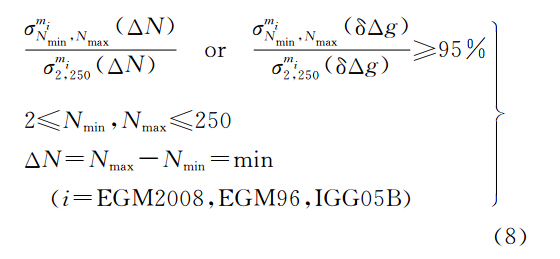2. 中国科学院大学,北京 100049;
3. 美国得克萨斯大学 空间研究中心,德克萨斯州 奥斯汀 78759;
4. 极地测绘科学国家测绘地理信息局重点实验室,湖北 武汉 430000
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Center for Space Research, University of Texas at Austin, Austin 78759, USA;
4. Key Laboratory for Polar Surveying and Mapping Science of State Adiministration of Surveying, Mapping and Geoinformation, Wuhan 430000, China
1 引 言
2009年3月17日ESA(European Space Agency)的GOCE(gravity field and steady-state ocean circulation explorer)卫星成功发射升空,标志着SGG(satellite gravity gradiometry)技术的首次实现,同时也是继CHAMP(challenging mini-satellite payload)、GRACE(gravity recovery and climate experiment)之后第3颗重力计划卫星的成功实施。GOCE卫星的科学目标是测定高精度和高空间分辨率的静态重力场,空间分辨率可达80~100 km,重力异常精度为1×10-5~2×10-5 m/s2,大地水准面误差限制在1~2 cm[1, 2]。至今,GOCE卫星已传回大量数据,GOCE数据参与解算的系列静态地球重力场模型[3, 4, 5, 6, 7, 8, 9]由ESA等相关研究机构对外公布。国内方面,文献[10]利用61 d的GOCE数据,采用高低卫卫跟踪和卫星重力梯度数据联合恢复重力场的最小二乘谱组合法,反演了2个180阶次的地球重力场模型WHU_GOCE_SC01S和WHU_GOCE_SC02S,结果显示整体精度优于GOCE时域解,而与GOCE空域解的精度相近。
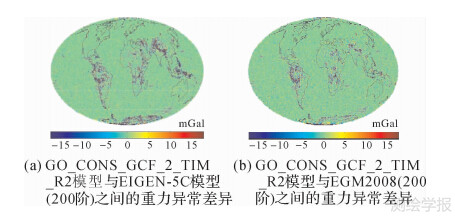
随着多个GOCE重力场模型的公布,其在全球各地区的适用性和精度评价开始成为各国研究人员关心的课题。如图 1所示,GO_CONS_GCF_2_TIM_R2模型[9](8个月GOCE数据)与其他系列代表性模型重力异常的比较显示:全球差异较大的区域主要集中在南美洲、非洲、青藏高原、南极等重力数据较少或空白的地区;中国差异较大的区域主要集中在西部地区特别是青藏高原等地形比较复杂、重力数据相对缺乏的区域。由SGG的测量原理和技术特点可知[1],GOCE数据相比其他重力卫星数据的优势在于中波段,而这种优势在地形复杂的区域往往会更加重要。而青藏高原作为世界上形成时代最晚、面积最大、平均海拔最高的高原,是地球上一个非常独特的地理单元,其地形十分复杂,地壳巨厚,地震和构造运动活跃,特别是整个高原的隆升机制以及喜马拉雅山系的形成等一些基本问题,至今存在许多争议,因此一直以来青藏地区是国际地学研究的中心和热点[11, 12]。
|
| 图 1 GO_CONS_GCF_2_TIM_R2模型与EIGEN-5C(200阶)模型及EGM2008(200阶)模型之间的重力异常差异 Fig. 1 Gravity anomaly deviations (D/O 200) of the GO_CONS_GCF_2_TIM_R2 from EIGEN-5C and EGM2008(1 mGal=10-5m/s2) |
重力学方法作为地球物理学和大地测量学的传统方法,在青藏高原构造运动和隆升进程研究中发挥着十分重要的作用,因此本文选取最高阶为250阶的GO_CONS_GCF_2_TIM_R2(下文简称GOCE-only(Ⅰ)模型)、GO_CONS_GCF_2_TIM_R3[9](下文简称GOCE-only(Ⅱ)模型(18个月GOCE数据))和GOCO02S[4] (8个月GOCE、7年GRACE、8年CHAMP、5年5个卫星的SLR数据)共3个GOCE重力场模型为验证对象,选择青藏地区作为研究区域,分别利用青藏地区GPS/水准和重力异常数据对GOCE重力场模型进行了外部测试。在测试过程中同时引入其他系列具有代表性的重力场模型(EGM2008[13],EGM96[14],ITG-Grace2010s[15],IGG05B(内部使用模型))作为比较,并对GOCE重力场模型与其他系列模型在青藏地区主要差异值的水平空间与垂直场源分布进行了详细的探讨和分析。
2 选用数据资料
2.1 重力场模型数据
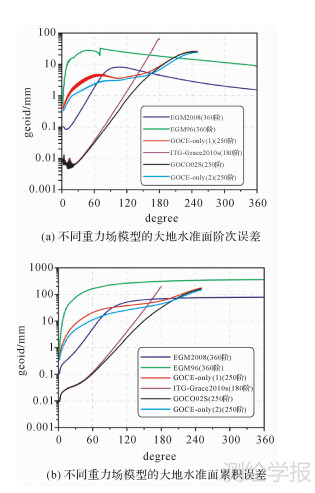
本文共选用了7个具有代表性的重力场模型(GOCE-only(Ⅰ)、GOCE-only(Ⅱ) 、GOCO02S、ITG-Grace2010s、EGM2008、EGM96、IGG05B),选用模型在国外的GPS/水准验证结果(表 1)显示: GOCE重力场模型精度很高,可达35~40 cm。图 2为选用模型的内符合误差评价(IGG05B模型解算过程中未给出内符合误差)。从图 2中可以清楚看出:① GOCE重力场模型相比其他模型的优势在于160阶前后的中波段;② GOCE-only(Ⅱ)模型相比GOCE-only(Ⅰ)模型精度有所改善;③GOCO02S相比GOCE-only(Ⅰ)和GOCE-only(Ⅱ)模型精度总体有所改善,特别是长波部分有了明显的改善。
| 模型名称(最大阶) | 美国/6169个点 | 加拿大/1930个点 | 欧洲/1235个点 | 澳大利亚/201个点 |
| GOCE-only(Ⅰ) (250) | 0.436 | 0.355 | 0.434 | 0.376 |
| GOCE-only(Ⅱ)(250) | 0.430 | 0.343 | 0.417 | 0.357 |
| GOCO02S (250) | 0.435 | 0.352 | 0.434 | 0.372 |
| ITG-Grace2010s(180) | 0.548 | 0.459 | 0.595 | 0.523 |
| EGM2008(2190) | 0.248 | 0.126 | 0.208 | 0.217 |
| EGM96(360) | 0.379 | 0.357 | 0.478 | 0.297 |
| IGG05B(360) | 0.388 | — | 0.325 | — |
|
| 图 2 不同重力场模型的大地水准面阶次误差与大地水准面累积误差 Fig. 2 Error degree amplitudes and error amplitudes as a function of maximum degree of different gravity field models in terms of geoid heights |
2.2 GPS/水准和重力异常数据
本文采用的GPS/水准数据为青藏地区GPS A/B级网及其基于A/B网的GPS水准联测数据,共260个点。采用重力异常数据空间分辨率为5′×5′,数据范围为70°E—150°E和25°N—40°N,该范围内中国地区主要采用我国实测重力数据,国外地区以及数据空白区由国外相关研究机构发布的重力数据进行填充,然后通过重力归算和改正,最终生成分辨率为5′×5′的重力异常(Δ g real)格网数据。
3 GOCE重力场模型在青藏地区的评价与分析
3.1 GOCE重力场模型的GPS/水准验证
3.1.1 GPS/水准的验证方法
重力场模型计算GPS/水准点高程异常的公式为[17]
式中,GM为地心引力常数;n和m分别为阶次;N为重力场模型的最大阶;θ和λ分别是余纬和经度;re为参考椭球面到地心的距离;h为 GPS 所测的大地高;γ为正常重力;a为椭球长半径;Cnm和Snm为完全正规化的 Stokes 球谐系数;Pnm为归一化的缔合勒让德多项式。 GPS /水准点的实测高程异常计算公式为
式中,H为水准所测的正常高。于是模型与实测高程异常的差值为
3.1.2GPS/水准验证结果
分别采用上述7个重力场模型的不同最大截断阶数(90、120、150、180、250、360、720、2190),严格利用式(1)—式(3)进行计算,结果见表 2。从表 2可以看出:① 我国GPS/水准所测与重力场模型计算所得的高程异常之间存在较大的系统偏差,约占总体误差70%左右,系统偏差可能是由于水准网以及我国高程基准与全球大地水准面之间的系统偏差引起[18],为了有效消除系统偏差本文采用四参数模型[17, 19],系统偏差消除后精度得到明显改善(见表 2中消除系统偏差后的标准差值);② 由EGM2008模型验证结果来看,重力场模型系数在720阶以后,对高程异常精度的改善已不明显,验证结果与文献[18]基本一致;③ GOCE-only(Ⅰ)、GOCE-only(Ⅱ)以及GOCO02S模型验证结果相比显示GOCE-only(Ⅱ)模型以及多个卫星数据的GOCO02S模型相比GOCE-only(Ⅰ)模型精度均有所改善,但改善幅度均不明显;④GOCE重力场模型与其他系列模型验证结果横向比较显示GOCE重力场模型在150、180阶相比EGM2008精度有所改善,而相比EGM96模型整体精度都有所改善。
3.2 GOCE重力场模型的重力异常验证
3.2.1 重力异常的验证方法
由重力场模型计算大地水准面上重力异常的公式[17]为
则模型与实测重力异常的差值为
3.2.2重力异常的验证结果
地球重力场模型不同的截断阶数,所对应的空间分辨率(半波长)也不相同,其具体关系为
| 最大阶次 | 90 | 120 | 150 | 180 | 250 | 360 | 720 | 2190 | |
| GOCE-only(Ⅰ) | |||||||||
| 最小值 | -1.156 | -0.433 | -0.465 | -0.430 | -0.675 | — | — | — | |
| 最大值 | 7.849 | 5.625 | 3.658 | 2.685 | 2.530 | — | — | — | |
| 均值 | 2.188 | 1.663 | 1.248 | 1.081 | 0.796 | — | — | — | |
| 标准差 | 2.226 | 1.506 | 1.164 | 0.933 | 0.747 | — | — | — | |
| 改正后 | 0.901 | 0.560 | 0.443 | 0.334 | 0.285 | — | — | — | |
| GOCE-only(Ⅱ) | |||||||||
| 最小值 | -1.145 | -0.423 | -0.452 | -0.440 | -0.708 | — | — | — | |
| 最大值 | 7.858 | 5.636 | 3.685 | 2.696 | 2.458 | — | — | — | |
| 均值 | 2.187 | 1.663 | 1.248 | 1.082 | 0.765 | — | — | — | |
| 标准差 | 2.227 | 1.507 | 1.167 | 0.937 | 0.735 | — | — | — | |
| 改正后 | 0.899 | 0.558 | 0.442 | 0.335 | 0.284 | — | — | — | |
| GOCO02S | |||||||||
| 最小值 | -1.148 | -0.426 | -0.457 | -0.425 | -0.662 | — | — | — | |
| 最大值 | 7.866 | 5.632 | 3.683 | 2.711 | 2.554 | — | — | — | |
| 均值 | 2.193 | 1.670 | 1.256 | 1.150 | 0.809 | — | — | — | |
| 标准差 | 2.227 | 1.508 | 1.165 | 0.901 | 0.751 | — | — | — | |
| 改正后 | 0.900 | 0.558 | 0.439 | 0.283 | 0.279 | — | — | — | |
| ITG-GRACE 2010s | |||||||||
| 最小值 | -1.158 | -0.435 | -0.439 | -0.718 | — | — | — | — | |
| 最大值 | 7.860 | 5.627 | 3.730 | 3.017 | — | — | — | — | |
| 均值 | 2.192 | 1.670 | 1.252 | 1.046 | — | — | — | — | |
| 标准差 | 2.225 | 1.505 | 1.164 | 1.013 | — | — | — | — | |
| 改正后 | 0.901 | 0.552 | 0.440 | 0.391 | — | — | — | — | |
| EGM2008 | |||||||||
| 最小值 | -1.172 | -0.492 | -0.444 | -0.496 | -0.875 | -0.350 | -0.184 | -0.111 | |
| 最大值 | 7.850 | 5.653 | 3.842 | 2.751 | 2.132 | 1.109 | 0.891 | 0.876 | |
| 均值 | 2.187 | 1.659 | 1.263 | 1.041 | 0.674 | 0.448 | 0.325 | 0.320 | |
| 标准差 | 2.220 | 1.473 | 1.191 | 0.960 | 0.704 | 0.378 | 0.281 | 0.280 | |
| 改正后 | 0.997 | 0.467 | 0.456 | 0.361 | 0.290 | 0.144 | 0.101 | 0.098 | |
| EGM96 | |||||||||
| 最小值 | -1.656 | -0.713 | -0.638 | -0.759 | -1.116 | -0.702 | — | — | |
| 最大值 | 8.884 | 5.807 | 3.906 | 2.987 | 2.810 | 2.261 | — | — | |
| 均值 | 2.145 | 1.634 | 1.299 | 1.118 | 0.782 | 0.586 | — | — | |
| 标准差 | 2.367 | 1.566 | 1.192 | 1.021 | 1.020 | 0.799 | — | — | |
| 改正后 | 1.015 | 0.608 | 0.451 | 0.393 | 0.387 | 0.384 | — | — | |
| IGG05B | |||||||||
| 最小值 | -1.148 | -0.572 | -0.551 | -0.482 | -0.506 | -0.362 | — | — | |
| 最大值 | 7.891 | 5.545 | 3.829 | 3.205 | 2.209 | 1.874 | — | — | |
| 均值 | 2.186 | 1.682 | 1.339 | 1.180 | 0.878 | 0.712 | — | — | |
| 标准差 | 2.233 | 1.487 | 1.146 | 0.960 | 0.726 | 0.553 | — | — | |
| 改正后 | 0.906 | 0.544 | 0.409 | 0.331 | 0.253 | 0.184 | — | — |
本文采用重力场模型最大截断阶数分别为90、120、150、180、250、360,验证中采用了两种滤波方法:① 利用式(4)计算生成空间分辨率为2°×2°、1.5°×1.5°、1.2°×1.2°、1°×1°、0.72°×0.72°、0.5°×0.5°的重力异常格网数据,再采用空域高斯低通滤波将实测数据5′×5′的格网值转换成与重力场模型截断阶数相对应的分辨率,然后按式(5)进行计算;② 取各重力场模型的最大阶利用式(4)计算生成分辨率5′×5′的重力异常格网值,然后与实测重力异常数据一同采用空域高斯滤波生成相应的空间分辨率,再利用式(5)进行计算,结果见表 3。 从表 3可以看出:① 第2种方法的验证结果比第1种方法的标准差整体小5×10-5 m/s2~1×10-4 m/s2的量级,精度显著提高(由于第1种方法中重力场模型在截取阶次时相当于在频域里面进行了一次低通滤波,而实测数据是在空域里进行滤波,因此两种数据不能在同一尺度进行比对,而第2种方法很好地解决了这个问题,这将为今后利用重力场模型计算格网数据时提供一种新的滤波方法);② 随着空间分辨率的提高,模型与实测数据之间的差异值逐渐增大,原因在于地形起伏的影响随着空间分辨率的提高越来越显著;③ GOCE-only(Ⅰ)、GOCE-only(Ⅱ)与GOCO02S这3个模型在青藏地区的精度相当;④ GOCE重力场模型与其他系列模型横向比较显示EGM96模型验证结果总体精度相对较差,IGG05B模型结果总体较好(由于IGG05B模型解算过程中加入了中国地区的实测重力数据,因此IGG05B模型与实测数据符合较好),在120阶前,GOCE重力场模型与EGM2008模型精度相当,但在150、180和250阶,GOCE重力场模型的精度都要优于EGM2008; GOCE重力场模型与ITG-GRACE2010s模型精度相当,但分辨率要高于ITG-GRACE2010s模型。
| 截断阶次 | 90 | 120 | 150 | 180 | 250 | 360 | |||||||
| 空间分辨率 | 2°×2° | 1.5°×1.5° | 1.2°×1.2° | 1°×1° | 0.72°×0.72° | 0.5°×0.5° | |||||||
| 验证结果 | ① | ② | ① | ② | ① | ② | ① | ② | ① | ② | ① | ② | |
| GOCE-only(Ⅰ) | |||||||||||||
| 最小值 | -47.89 | -14.29 | -63.97 | -33.96 | -71.15 | -30.47 | -72.34 | -53.63 | -105.94 | -80.54 | — | — | |
| 最大值 | 43.14 | 28.10 | 63.05 | 46.90 | 79.38 | 52.81 | 95.52 | 66.29 | 106.24 | 77.25 | — | — | |
| 均值 | 0.83 | 0.65 | 1.23 | 0.98 | 0.45 | 0.38 | 0.62 | 0.56 | 0.72 | 0.67 | — | — | |
| 标准差 | 18.18 | 6.01 | 19.62 | 9.05 | 22.78 | 11.12 | 22.60 | 13.22 | 23.64 | 16.27 | — | — | |
| GOCE-only(Ⅱ) | |||||||||||||
| 最小值 | -48.03 | -18.33 | -79.87 | -38.27 | -90.06 | -35.79 | -72.46 | -61.02 | -112.03 | -82.37 | — | — | |
| 最大值 | 43.06 | 30.01 | 70.35 | 45.25 | 86.85 | 55.26 | 95.34 | 79.87 | 109.04 | 78.41 | — | — | |
| 均值 | 0.82 | 0.85 | 0.89 | 0.65 | 0.62 | 0.65 | 0.62 | 0.72 | 0.70 | 0.73 | — | — | |
| 标准差 | 18.20 | 6.22 | 19.54 | 8.96 | 22.14 | 11.07 | 22.62 | 13.28 | 23.52 | 16.32 | — | — | |
| GOCO02S | |||||||||||||
| 最小值 | -48.04 | -14.16 | -64.16 | -33.76 | -71.02 | -30.29 | -72.27 | -53.19 | -104.63 | -79.69 | — | — | |
| 最大值 | 43.00 | 28.17 | 63.21 | 46.64 | 79.52 | 52.77 | 95.51 | 65.39 | 106.11 | 77.25 | — | — | |
| 均值 | 0.84 | 0.66 | 1.24 | 0.71 | 0.46 | 0.38 | 0.63 | 0.57 | 0.73 | 0.68 | — | — | |
| 标准差 | 18.17 | 6.00 | 19.61 | 8.75 | 22.77 | 11.10 | 22.59 | 13.17 | 23.50 | 16.20 | — | — | |
| ITG-GRACE2010s | |||||||||||||
| 最小值 | -48.06 | -12.73 | -64.23 | -27.73 | -71.37 | -40.54 | -77.32 | -43.12 | — | — | — | — | |
| 最大值 | 42.97 | 29.32 | 63.28 | 41.87 | 78.98 | 58.08 | 99.64 | 70.10 | — | — | — | — | |
| 均值 | 0.92 | 0.68 | 1.24 | 0.63 | 0.44 | 0.40 | 0.59 | 0.59 | — | — | — | — | |
| 标准差 | 18.25 | 5.87 | 19.62 | 8.56 | 22.73 | 11.20 | 23.04 | 13.40 | — | — | — | — | |
| EGM2008 | |||||||||||||
| 最小值 | -48.67 | -22.04 | -74.21 | -19.85 | -70.74 | -54.21 | -77.27 | -77.52 | -94.83 | -89.26 | -144.84 | -121.16 | |
| 最大值 | 40.54 | 32.14 | 70.68 | 40.08 | 93.98 | 79.57 | 97.68 | 70.32 | 115.16 | 97.50 | 179.30 | 161.95 | |
| 均值 | 0.84 | 0.58 | 1.19 | 0.54 | 0.43 | 0.23 | 0.60 | 0.30 | 0.59 | 0.54 | 0.64 | 0.56 | |
| 标准差 | 18.04 | 6.549 | 19.76 | 8.63 | 22.61 | 12.62 | 22.84 | 13.78 | 25.90 | 18.36 | 29.53 | 23.78 | |
| EGM96 | |||||||||||||
| 最小值 | -49.41 | -35.74 | -48.53 | -47.31 | -78.44 | -53.33 | -107.77 | -87.69 | -127.29 | -108.77 | -187.51 | -155.63 | |
| 最大值 | 44.37 | 47.64 | 76.59 | 73.08 | 132.52 | 139.38 | 130.57 | 86.88 | 285.12 | 245.19 | 349.16 | 296.40 | |
| 均值 | 0.86 | 0.65 | 1.06 | 0.53 | 0.46 | 0.40 | 0.59 | 0.36 | 0.49 | 0.47 | 0.61 | 0.55 | |
| 标准差 | 19.20 | 9.93 | 20.86 | 13.18 | 24.59 | 16.31 | 25.46 | 15.94 | 29.95 | 22.47 | 32.92 | 26.64 | |
| IGG05B | |||||||||||||
| 最小值 | -47.79 | -12.58 | -63.70 | -16.22 | -64.27 | -23.53 | -70.42 | -27.58 | -59.50 | -35.37 | -72.18 | -51.89 | |
| 最大值 | 42.97 | 21.98 | 62.02 | 28.77 | 77.62 | 47.23 | 65.35 | 40.17 | 91.28 | 69.19 | 133.01 | 96.54 | |
| 均值 | 0.85 | 0.66 | 1.27 | 0.75 | 0.67 | 0.52 | 0.82 | 0.67 | 0.77 | 0.76 | 0.89 | 0.81 | |
| 标准差 | 18.00 | 5.07 | 19.17 | 6.79 | 20.23 | 8.96 | 18.28 | 9.49 | 18.75 | 12.40 | 20.18 | 14.87 | |
4 GOCE重力场模型与其他系列模型的差异性分析
4.1 GOCE重力场模型与其他系列模型主要差异值的水平空间分布
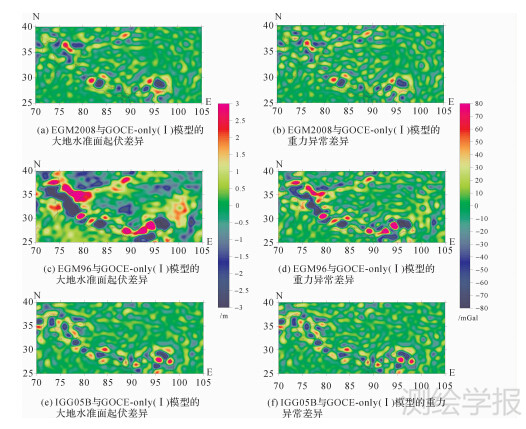
本文选取EGM2008、EGM96、IGG05B和GOCE-only(Ⅰ) (由于GOCE-only(Ⅰ)、GOCE-only(Ⅱ)和GOCO02S 3个模型彼此之间在青藏地区验证结果差别甚微,因此只取GOCE-only(Ⅰ)模型作比较)4个重力场模型,最大阶次都取250,根据式(1)和式(4)分别计算出各模型在青藏地区的大地水准面起伏和重力异常,然后将EGM2008、EGM96、IGG05B模型分别与GOCE-only(Ⅰ)模型进行比较。结果(图 3)显示,3个模型与GOCE-only(Ⅰ)模型的总体差异虽然各不相同。但是主要差异值的分布呈现一致性,都分布在喜马拉雅山脉、昆仑山等地形较为复杂的高山区。从表 4可知,在青藏地区GOCE-only(Ⅰ)模型与EGM2008模型最为符合,IGG05B次之,EGM96最差,但在中国边境内GOCE-only(Ⅰ)模型与IGG05B最为符合,EGM2008次之,EGM96最差。
|
| 图 3 EGM2008、EGM96、IGG05B模型与GOCE-only(Ⅰ)模型比较的大地水准面和重力异常差异 Fig. 3 Geoid height and gravity anomaly deviations of the GOCE-only(Ⅰ) from EGM2008,EGM96 and IGG05B |
| GOCE-only(Ⅰ) /其他模型 | 青藏地区 | 中国境内 | 数据类型 |
| EGM2008 | 0.565 | 0.234 | |
| EGM96 | 1.535 | 0.726 | |
| IGG05B | 0.607 | 0.201 | 大地水准面/m |
| EGM2008 | 14.335 | 6.245 | |
| EGM96 | 25.519 | 15.369 | |
| IGG05B | 15.785 | 5.846 | 重力异常/(10-5m/s2) |
4.2 GOCE重力场模型与其他系列模型主要差异值的阶次与垂直场源分布
虽然通过图 3能够分别以大地水准面和重力异常的形式得知GOCE-only(Ⅰ)模型与EGM2008、EGM96和IGG05B模型主要差异值的水平空间分布,但是却无法得知其主要差异值的在地球内部的垂直分布,根据文献[20] 给出的重力场球谐函数阶次(n)与场源深度(D)的简单近似关系式
可以得知,重力场模型的不同阶次所对应的垂直场源深度也不同。为了了解模型之间主要差异值的垂直场源分布,需先求出主要差异值的阶次分布,本文根据统计分析的基本原理,利用差值均方根所代表的含义设计了一种新方法,能够精确的找出 GOCE重 力场模型与其他系列模型主要差异值的阶次分布。 首先,分别计算出 EGM2008、EGM96、IGG05B这3个模型与GOCE-only(Ⅰ )之间(2~250阶)大地水准面和重力异常差值的均方根σmi 2,250( Δ N)、σmi 2,250( δΔ g),然后在2~250阶中选用不同的最小(N min )、最大(N max )阶次,计算出N min ~N max 之间大地水准面和重力异常差值的均方根σmi N min ,N max ( Δ N)、σmi N min ,N max ( δΔ g)。当以上变量满足以下条件时
得出未知量N min 和 N max ,此时认为模型之间的主要差异值分布在N min 到 N max 之间。最后根据式(7)计算出垂直场源深度D min 和D max 。 计算结果(表 5)显示:3个模型与GOCE-only(Ⅰ)模型之间主要差异值的垂直场源深度主要分布在岩石圈,只有EGM96与GOCE-only(Ⅰ)模型之间的大地水准面主要差异值的场源深度超过青藏地区岩石圈深度达到255 km的软流层。
| GOCE-only(Ⅰ)/其他模型 | N min~ N max /阶 | D min~ D max/km | 场源深度 | 数据类型 |
| EGM2008 | 96~247、97~248、98~249、99~250 | 26~66 | 岩石圈 | |
| EGM96 | 26~180 | 36~255 | 岩石圈、软流层 | |
| IGG05B | 118~230 | 28~54 | 岩石圈 大地水准面 | |
| EGM2008 | 122~250 | 26~53 | 岩石圈 | |
| EGM96 | 66~247、67~248、68~249、69~250 | 26~98 | 岩石圈 | |
| IGG05B | 121~239、122~240、123~241 | 27~53 | 岩石圈 重力异常 |
4.3 GOCE重力场模型相比EGM2008模型优势阶分析
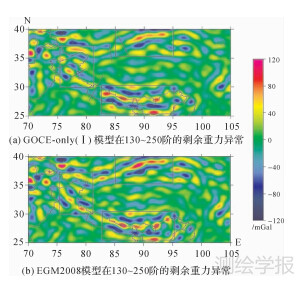
目前为止,国际上公认的最好重力场模型为EGM2008模型,通过对表 3中重力异常各阶次验证精度(标准差)的趋势进行线性化分析得出: 在青藏地区GOCE重力场模型相比EGM2008的重力异常优势主要集中在中波段约为130~250阶。图 4可以看出:对整个青藏地区而言,两个模型所计算的130~250阶剩余重力异常的总体分布形态未出现较大差异,但在局部地区(图中长方形标注)出现了较为明显的差异,且GOCE重力场模型显示出较多的重力异常不连续带(图中直线标注),它们可能是区域性大断层或区域韧性剪切带[21]。因此对于整个青藏地区,GOCE重力场模型相比EGM2008模型重力异常在中波段(130~250阶)以及局部区域精度有明显提高。
|
| 图 4 GOCE-only(Ⅰ) (130~250阶)模型与EGM2008(130~250阶)模型在青藏地区的剩余重力异常 Fig. 4 Residual gravity anomaly computing by GOCE-only(Ⅰ) (D/O 130~250) and EGM2008 (D/O 130~250) in Qinghai-Tibet region |
5 结 论
随着GOCE卫星数据不断的积累,GOCE数据解算方法包括局部求解方法[22]的发展,GOCE重力梯度数据恢复的青藏高原重力场模型精度也将得到进一步改善,GOCE重力场模型给出的分层深度重力信息,有助于对青藏地区岩石圈内部构造及动力学特性等重大问题产生新的理解和认识[23]。 本文采用青藏地区GPS/水准和实测重力数据,分别对GOCE以及其他代表性重力场模型在青藏地区进行了外部测试,得出GOCE重力场模型在青藏地区高程异常的精度约为75 cm,重力异常的精度约为2×10-4 m/s2。在重力异常精度验证中引入一种新的滤波方法,精度相比传统方法提高5×10-5~10×10-5 m/s2。同时首次采用统计分析的方法精确找出GOCE重力场模型与其他模型之间最大差异值的阶次和垂直场源分布,结果显示:在青藏地区模型之间最大差异值在空间水平方向主要分布在喜马拉雅山脉与昆仑山脉等地形起伏较大的地区,阶次上主要集中在中波段,转化为垂直场源深度后在岩石圈。下一步工作将结合青藏地区地质、地震等资料,并利用GOCE重力场模型进行重力联合反演,从而将有助于对青藏地区岩石圈构造产生更加深刻的认识。
致谢: 感谢德国地球科学中心(GFZ)和欧空局(ESA)提供重力场模型数据。| [1] | European Space Agency. Gravity Field and Steady-state Ocean Circulation Mission[R]. Reports for Mission Selection, The Four Candidate Earth Explorer Core Missions. Noordwijk: ESA Publication Division, 1999: 9-27. |
| [2] | DRINKWATER M, FLOBERGHAGEN R, HAAGMANS R, et al. GOCE: ESA’s First Earth Explorer Core Mission[J]. Space Science Reviews, 2003, 108(1): 419-432. |
| [3] | FOERSTE G, BRUINSMA S, SHAKO R, et al. EIGEN-6: A New Combined Global Gravity Field Model Including GOCE Data from the Collaboration of GFZ-Potsdam and GRGS-Toulouse[J]. Geophysical Research Abstracts, 2011, 13: 1-13. |
| [4] | GOIGINGER H, HOECK E, RIESER D, et al. The Combined Satellite-only Global Gravity Field Model GOCO02S[R]. Vienna: The 2011 General Assembly of the European Geosciences Union, 2011. |
| [5] | PAIL R, GOIGINGER H, SCHUH W D, et al. Combined Satellite Gravity Field Model GOCO01S Derived from GOCE and GRACE[J]. Geophysical Research Letters, 2010, 37(20): 203-214. |
| [6] | BRUINSMA S L, MARTY J C, BALMINO G, et al. GOCE Gravity Field Recovery by Means of the Direct Numerical Method[R]. Bergen: The ESA Living Planet Symposium, 2010. |
| [7] | PAIL R, GOIGINGER H, MAYRHOFER R, et al. Global Gravity Field Model Derived from Orbit and Gradiometry Data Applying the Time-wise Method[C]// Proceedings of ESA Living Planet Symposium. Bergen: ESA Publication Division, 2010:101-108. |
| [8] | MIGLIACCIO F, REGUZZONI M, GATTI A, et al. A GOCE-only Global Gravity Field Model by the Space-wise Approach[C]// Proceedings of the 4th International GOCE User Workshop. Munich: ESA Publication Division, 2011: 1-8. |
| [9] | PAIL R, BRUINSMA S, MIGLIACCIO F, et al. First GOCE Gravity Field Models Derived by Three Different Approaches[J]. Journal of Geodesy, 2011, 85(11): 819-843. |
| [10] | ZHONG Bo, LUO Zhicai, LI Jiancheng, et al. Spectral Combination Method for Recovering the Earth’s Gravity Field from High-low SST and SGG Data[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 735-742. (钟波, 罗志才, 李建成, 等. 联合高低卫-卫跟踪和卫星重力梯度数据恢复地球重力场的谱组合法[J]. 测绘学报, 2012, 41(5): 735-742.) |
| [11] | XU Houze, WANG Yong, LU Yang, et al. The Geodesy Research of the Tibetan Plateau[M]. Wuhan: Hubei Science and Technology Press, 2000: 1-2. (许厚泽, 王勇, 陆洋, 等. 青藏高原的大地测量研究[M]. 武汉: 湖北科学技术出版社, 2000: 1-2.) |
| [12] | JIANG Weiping, ZHOU Xiaohui, LIU Jingnan, et al. Present-Day Crustal Movement and Strain Rate in the Qinghai-Tiban Plateau from GPS Data[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(3): 285-292. (姜卫平, 周晓慧, 刘经南, 等. 青藏高原地壳运动与应变的GPS监测研究[J]. 测绘学报. 2008, 37(3): 285-292.) |
| [13] | PAVLIS N K, HOLMES S A, KENYON S C, et al. An Earth Gravitational Model to Degree 2160: EGM2008[R]. Vienna: General Assembly of the European Geosciences Union, 2008: 13-14. |
| [14] | LEMOINE F G, KENYON S C, FACTOR J K, et al. The Development of the Joint NASA GSFC and the National Imagery and Mapping Agency (NIMA) Geopotential Model EGM96[R]. Greenbelt: NASA/TP-1998-206861, Goddard Space Flight Center, 1998. |
| [15] | MAYER-GVRR, KURIENBACH T E, EICKER A. ITG-Grace2010 Gravity Field Model[EB/OL]. [2012-10-21]. grace2010.) |
| [16] | GFZ. Root Mean Square about Mean of GPS/Levelling Minus Gravity Field Model Derived Geoid Heights[EB/OL].[2012-10-21].) |
| [17] | HEISKANEN W A , MORITZ H. Physical Geodesy[M]. San Francisco: Freeman, 1967. |
| [18] | ZHANG Chuanyin, GUO Chunxi, CHEN Junyong, et al. EGM2008 and Its Application Analysis in Chinese Mainland[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 283-289. (章传银, 郭春喜, 陈俊勇, 等. EGM2008地球重力场模型在中国大陆适用性分析[J]. 测绘学报, 2009, 38(4): 283-289.) |
| [19] | ZENG Yuanwu, YANG Zhanji, ZHANG Tianji. Evaluation of EGM96, WDM94 and GPM98CR Geo-potential Models for Representing the Local Gravity Field of Shenzhen, China[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(4): 289-291. (曾元武, 杨沾吉, 张天纪. EGM96, WDM94和GPM98CR高阶地球重力场模型表示深圳局部重力场的比较与评价[J]. 测绘学报, 2002, 31(4):289-291.) |
| [20] | BOWIN C. Depth of Principal Mass Anomalies Contributing to the Earth’s Geoidal Undulation and Gravity Anomalies[J]. Marine Geodesy, 1983, 7(1-4): 61-100. |
| [21] | YUAN Xuecheng. 3D Lithospheric Structure of Western China and Its Enlightenment on Petroleum Prospecting[J]. Geology in China, 2005, 32(1):1-12. (袁学诚. 论中国西部岩石圈三维结构及其对寻找油气资源的启示[J]. 中国地质, 2005, 32(1): 1-12.) |
| [22] | GAO Chunchun, LU Yang. Study Progress in Regional Gravity Field Recovery Using Satellite Gravity Gradiometry[J]. Hydrographic Surveying and Charting, 2012, 32(1): 71-75. (高春春, 陆洋. 利用卫星重力梯度恢复局部重力场的研究进展[J]. 海洋测绘, 2012, 32(1): 71-75.) . |
| [23] | FIELDING E J, MCKENZIE D. Lithospheric Flexure in the Sichuan Basin and Longmen Shan at the Eastern Edge of Tibet[J]. Geophysical Research Letters, 2012, 39(9): 93-101. |