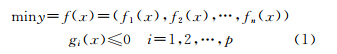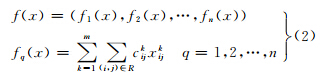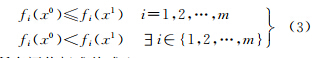Corresponding author:LU Feng E-mail:luf@lreis.ac.cn
多模式路径规划旨在为出行者提供涉及多种交通模式的出行路径方案。与单一模式路径规划相比,多模式网络环境下的路径规划更加复杂,需要考虑多种交通模式的组合方式与换乘耗费等问题。另一方面,传统的单一标准路径查询,如最短距离、理想最少时间路径查询等,已经不能满足现代城市多模式立体交通体系下公众出行的现实需求。从出行者的角度来看,满足多种标准的出行路径方案更适应个体的特殊需要;从出行服务提供者的角度来看,在多模式交通环境中,充分考虑多种个性化需求、量身定做的多标准出行路径规划服务,更能够适应市场的需求。
1 多标准路径问题
多标准(或多目标)路径规划是同时考虑多于一种评价标准的路径求解问题。其本质在于,在大多数情况下,某一标准(或目标)性能的提高可能引起其他标准(或目标)性能的降低。同时使多个目标均达到最优几乎是不可能的,因此只能在各目标之间进行协调权衡和折衷处理,使所有目标函数尽可能达到最优。多标准路径问题的结果不再是单一解,而是一个Pareto最优解集。解集中的解相互间不存在优劣关系。多标准路径规划是具有NP特性的多标准决策问题,通常有两种解决思路,即多标准转化为单标准路径算法和单标准改造为多标准路径算法。
多标准转化为单标准路径算法通过一定策略将多标准问题转化为单标准标量值,从而应用单标准路径算法进行计算。又可分为两类:目标加权法和策略约束法。前者采用线性加权求和等方法,很难确定科学合理的权重值[1, 2],并且不能在非凸的均匀曲面上得到所有最优解[3]。后者将k个标准中的k-1个标准转换为约束条件,其结果主要依赖于被确定为目标函数的单标准,可能高估了某一标准的作用,并且可能导致该单标准问题无解[4]。文献[5]从预先指定搜索空间的角度进行多标准研究,本质上还是要预先确定各标准的权重。
单标准改造为多标准路径算法可分为多标准标号算法和进化算法。多标准标号算法将图模型中的节点或边的标号由一维扩展为多维,多维之间相互独立。文献[6]基于文献[7]的双标准标号算法,提出了多标号算法,建立了一种求解连续线性多目标问题的方法。此后,出现了多种标号算法求解该问题[8, 9, 10]。标号算法通过比较每一步当前的最优结果,理论上可以找到最优结果(如果有解),但是,该方法时间复杂度高,对于大规模真实网络不具可行性。在多模式环境下,多种出行标准下会产生不同的交通模式组合情况,使得问题变得更加复杂。
遗传算法(genetic algorithm,GA)是一类借鉴生物界的进化规律演化而来的智能优化方法,能够有效避免不同标准权重人为分配问题;由于它固有的并行性,进化过程同时处理一代种群(解集),结果不限于单一解,非常适合求解复杂的多目标问题。此外,由不同模式下的路径段组合而成的多模式路径与遗传学中由遗传基因构成的染色体具有结构上的相似性,因此,可以考虑采用遗传算法解决该问题。
GA在路径规划中已有应用。在路径编码研究方面,编码方式的改进可以提高搜索效率,如基于优先权的路径编码方法[11]和基因值顺序表示该基因连接的后续基因位置[12]的编码方法。但是,这两种定长染色体编码方法的空间复杂度较高,对大规模网络缺乏可行性。一些学者提出了利用遗传算法解决单标准路径问题的方法,如TSP[13]、k则最短路径[14]、VRP[15]、最短路径优化[16]、公交线路优化[17]等。也有部分学者研究了单一交通模式下的多标准路径问题,包括针对开放空间的三维环境路径规划[18]和针对网络受限空间的路径规划[3, 19]等。关于多模式环境下的多标准路径规划问题,文献[20—21]提出了一种适应换乘网络的遗传算法。但该方法限于公共交通或步行换乘网络,无法支持具有复杂结构的公交模型,并且存在染色体编码冗余。
本文利用GA求解多标准问题的优势,结合多模式路径的特点,提出一种基于遗传算法的多模式多标准路径规划方法。
2 多模式多标准路径方法
2.1 染色体编码与解码
染色体编码,是将待求解的问题由表现型空间转换到基因型,以便于进行遗传操作。相对而言,染色体解码就是建立从基因型空间到表现的映射。针对本文研究的道路网络而言,一条路径用所经过的道路ID进行个体编码可以减小数据冗余、实现精确导航并且易于解码。
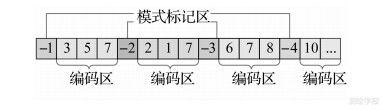
多模式路径要求个体编码能够体现多种交通模式组合,同时又不产生过多数据冗余;遗传算法要求个体编码易于遗传算子操作。因此,定义多模式个体(染色体)编码为:采用带模式标识的不定长表现型编码,由模式标记区与ID编码区组成(如图 1)。模式标记可以采用任意类型表示,仅用作区分不同模式,表示其后至下一模式标记前的基因段属于同一种模式。在图 1中,设-1、-2、-3、-4分别表示驾车、公交、地铁、步行等模式,则-1后,-2前的基因段为驾车模式经过的路段ID。
|
| 图 1 多模式路径染色体编码示意图 Fig. 1 Chromosome encoding for multi-modal routes |
2.2 适应性评价
解的适应性评价在遗传算法中扮演环境的角色,根据个体的适应值进行评定[22]。多标准问题中,目标函数可以表达为
式中,n为目标个数;fi(x)为某单一目标下的目标函数;gi(x)为限制条件。
具体在多模式多标准路径问题上,表现为在不同评价标准下的路径的计算值,有
限制条件
xkij-xkji=-1j为起点1j为终点0j为非起止点 xkij=1 边(i,j)在路径中0其他 k=1,2,…,m
式中,n为目标个数;m为模式个数;上标k表示不同模式;xkij 表示在某一模式中边(i,j)是否在路径中;ckij 为边(i,j)的耗费,在不同评价标准下代表不同的含义。如最短路径标准下cij表示长度,最短时间标准下cij表示时间等。由此,公式(1)的计算结果是一个p-维向量,每一维度代表一种标准下的路径评价值。因此,根据p-维向量进行比较得到的结果并非单一解,而是一个解集,即Pareto优化解集。向量间的比较采用“支配”概念进行描述。
定义:若解x0支配解x1(记为x0 x1),当且仅当
对所有评价标准均成立。
在向量比较的基础上,对解集中的解进行Pareto最优排序,并分配适应值。可以采用多种排序方法,如Fonseca等的Pareto排序方法[23],个体的排序数等于当前种群中支配他的个体的数目加1,所有非劣个体排序值为1,并以此作为个体适应值。
2.3 进化算子
由于传统单模式路径问题中的遗传算子针对的个体编码是同质的,各个位置的基因性质对等,可以进行任意交叉及变异。但是在多模式路径中,不同模式间的基因段之间是异质的,也就是说,不同交通模式中的路径性质不对等,不可实现任意点任意模式的换乘。因此,要重新定义满足多模式路径特征的遗传算子。遗传算子通过对基因进行交叉、变异,生成新个体,即得到新路径。因此,定义crossover与mutation算子分别为模式内交叉与变异算子,即只在相同模式内进行遗传算子操作。定义hypercrossover与hypermutation算子分别为模式间交叉与变异算子,即只在不同模式间进行遗传算子操作。
模式内交叉与变异算子的特点是,不引入新的交通模式,即最大化控制换乘次数的增加。模式间交叉与变异算子的特点是,算子操作会引起交通模式换乘次数上的增加,因此在具体操作中要采取一定措施控制其他标准的优化。
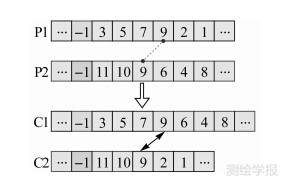
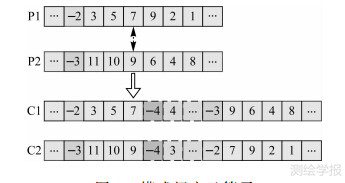
模式内交叉算子运算采用单点交叉策略(图 2),并进行环路检验与修复。模式间交叉算子运算的基本思想是:首先探测每个个体的模式标记,并组合成交叉组合对,随机选择一个组合;然后,探测所有可能的交叉基因对,随机选择一对组合进行单点交叉运算;最后,进行环路检验与换乘缝隙探测。模式间交叉算子运算后有可能产生连接缝隙,即换乘缝隙(如公交换乘地铁),通常需要借助其他交通模式(如步行等)进行连接,如图 3中采用模式-4。
|
| 图 2 模式内交叉算子 Fig. 2 Intra-modal crossover operator |
|
| 图 3 模式间交叉算子 Fig. 3 Inter-modal crossover operator |
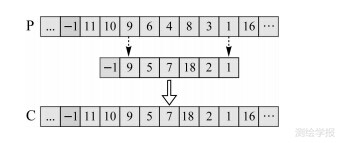
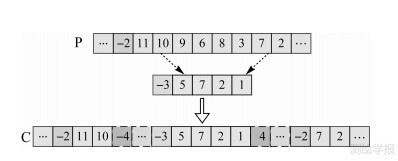
模式内变异算子运算(图 4)通过探测可变基因对,在该模式下产生新的基因段序列代替原序列中可变基因间的基因段实现变异。模式间变异算子运算(图 5)采用定向变异策略,加速优秀个体产生。其基本思想是首先探测模式标记,根据定向变异概率确定变异目标模式;然后,在该目标模式下生成新基因段代替原基因段;最后,合并非必要的连续模式内换乘并进行环路检验与换乘缝隙探测。模式间变异算子产生的新个体同样可能存在换乘缝隙,可借助其他模式进行无缝连接。
|
| 图 4 模式内变异算子 Fig. 4 Intra-modal mutation operator |
|
| 图 5 模式间变异算子 Fig. 5 Inter-modal mutation operator |
选择算子运算根据定义种群大小G和新种群当前个体数G′确定选择的优秀个体数量X=G-G′。G′由交叉与变异算子生成的新个体组成,优秀个体的选择方法为:统计评价值为1的非重复个体数目M,若X≤M,则随机选择当前评价值的非重复个体进入下一代种群;若X>M,则当前非重复最优个体进入下一代,然后按照二元锦标赛方法确定优秀个体进入下一代种群,直至达到选择数目。
2.4 计算流程
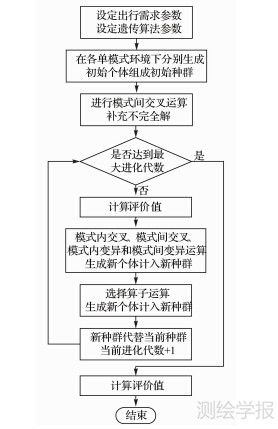
本文提出的多模式多标准遗传算法流程如图 6所示。
|
| 图 6 多模式多标准遗传算法流程 Fig. 6 GA based multi-modal multi-criteria routing |
出行需求参数包括起点、终点、出行模式、出行标准与出行时间等。
需要指出的是,该算法流程采用满足最大进化代数作为进化停止标志,在实际应用中,也可以以两代之间适应度之差小于某个固定值,或者以满足一定更新数变化为0的连续进化代数作为结束条件。
3 试验分析与讨论
本文在多模式交通网络逻辑一体化模型[24]的基础上,以北京五环内交通网络为试验对象实现了该方法。试验数据涉及步行、自行车网络(包含步行段52 509条)、行车网络(包含车行道段54 007条)、公交网络(公交线186条,站点4160个)及地铁网络(轨道段124条,站点113个)等出行模式。评价标准涉及最短时间、最小费用、最少换乘次数。针对各种交通模式,在不同评价标准下构建了相应的计算模型[24],其中,时间标准计算基于浮动车系统获取的道路路况,并考虑各种时间耗费,如路口等待时间、换乘耗时等;费用标准计算采用北京市公交、地铁、出租车通用计费标准;换乘次数标准中,短距离步行连接不计入总换乘次数中。
试验中随机选取了839个点作为起止点。由于本研究中所采用数据在各种单一出行模式下ID编码非负唯一,因此,可以采用负值区分各种模式(如图 1中-1、-2、-3、-4)。在ID编码中,既可以采用弧段ID也可以采用节点ID,本研究中对行车网络和步行网络采用弧段ID,对公交网络和地铁网络采用节点ID。
在设定起止点和遗传算法参数后,首先,在各单模式环境下,分别在起止点一定范围内,生成一定数量的初始个体,此时生成的个体可能不完全覆盖起止点路径(如:地铁模式不能连接任意两个起止点),称之为不完全个体;对该群体进行模式间交叉算子运算,补充不完全个体为完全个体(覆盖起止点的路径);然后按照计算流程进行计算,直至满足终止条件,本试验中采用固定最大进化代数。对于个体的生成算法,可以采用成熟的单标准路径规划算法。
业界对遗传初始种群个数对算法的影响存在一定争议[25],但是普遍认可其对算法的空间复杂度的影响;对进化参数迄今没有公认的确定方法,但存在一些普遍的指导思想,对交叉和变异算子在进化前期与后期的作用有相应研究;针对不同的目的,参数设置也会出现不同。
针对本文提出的方法,初始个体在各种交通模式中均有体现,一方面可以增加进化开始阶段的种群多样性,确保各种交通模式参与到进化过程中;另一方面,不定长的编码方式在多模式交通环境能够有效控制空间耗费。进化代数是给定的算法结束标志,其合理取值通常需要通过试验获取。交叉、变异算子都是为了产生新个体,其运算概率直接影响路径结果。由于本方法中变异算子突破了传统遗传算法中的含义,作为一种有效的模式转换手段,变异与交叉重要程度相近;另外,由于模式间变异一定会产生换乘次数的增加(采用定向变异策略可消除部分影响),因此,其变异概率可略小于交叉概率。选择算子保留一定数量的优秀个体直接进入下一代,过大会导致过早陷入局部解;过小,体现不出算子意义。通常情况下保留10%~20%的精英个体。
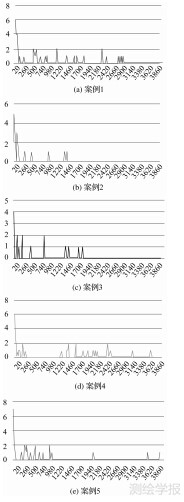
为了确定进化参数的影响,分别采用了5种参数分配案例进行试验,各案例参数取值见表 1,种群大小设为100,进化代数4000。定义从父代到子代产生新最优个体的数目为更新数。更新数表明遗传进化是否有新最优个体产生。如果更新数为0,最优个体表现值未发生变化,若持续多代均保持该数值,则认为进化趋于稳定;若不为0,则表示产生新的最优个体。对位于试验区对角域内的直线距离10km以上的某一随机O-D对进行遗传算法运算,得到更新数变化图(如图 7)。
| pc | phc | pm | phm | |
| 案例1 | 0.25 | 0.25 | 0.15 | 0.15 |
| 案例2 | 0.35 | 0.35 | 0.05 | 0.05 |
| 案例3 | 0.05 | 0.05 | 0.35 | 0.35 |
| 案例4 | 0.20 | 0.20 | 0.20 | 0.20 |
| 案例5 | 0.25 | 0.15 | 0.25 | 0.15 |
注:pc=模式内交叉概率;phc=模式间交叉概率;pm=模式内变异概率;phm=模式间变异概率。
图 7中,横轴为进化代数(每20代一统计),纵轴为更新数目。从进化更新数变化可以看出,案例1、2、3进化趋于稳定,案例4、5仍在进化。进一步对同一O-D的4000代进化后的结果进行比较发现,在案例1得到的5个最优个体中有3个个体在所有最优结果个体中占优;案例4的4个最优个体中有两个在所有个体中占优;其他案例结果均未得到最优结果。在对试验区内其他随机O-D进行的试验中发现,不同O-D对于概率参数的敏感程度不同,除案例2达到稳定的代数较早(1500代以内)外,其他案例并无明确先后顺序,但对其结果进行比较发现,案例1和案例4的参数得到的结果相对而言更易于在对比结果中取得最优。
以上试验结果基本上验证了先前的分析,因此,对于本文提出的方法,交叉概率等于或略高于变异概率时容易获得较好解。对于进化代数的确定,可以在设置最大进化代数基础上,通过本方法中的更新数以一定代数不变化作为结束标志。根据该算法的设计,进化过程中每个个体都是完整的一个路径结果,因此,无论采用哪种概率方案,均可得到可用解。
|
| 图 7 更新数变化对比 Fig. 7 Scenarios with new generated number |
按照案例1的参数进行计算,经过4000代进化达到稳定后结果见表 2。
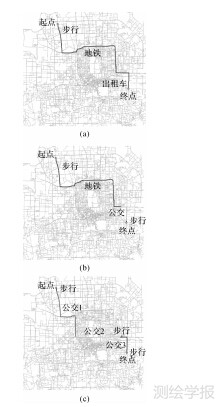
表 2所示为达到最大进化代数后的Pareto最优解统计结果。其中,T、W、B与S分别代表出租车、步行、公交与地铁模式。该结果集涉及单模式路径结果,如出租车、步行、自行车等;传统换乘模式组合,如公交换乘组合等;对于时间耗费较少的组合,显示了较强的实用性方案,如出租车-地铁-出租车、地铁-出租车、地铁-公交等;对于地铁-出租车-公交模式在预算控制和时间控制的平衡上表现较好。从各标准的满足上,能够体现不同需求,用户可根据自身需要选择合适的路径方案出行。部分结果可视化如图 8所示,8(a)为地铁换乘出租带有步行连接,8(b)为地铁换乘公交带有步行连接,8(c)为公交换乘带有步行连接。
| 时间/min | 费用/元 | 换乘次数 | 换乘模式 |
| 253 | 0 | 0 | W |
| 43 | 40 | 0 | T |
| 36 | 26 | 1 | (W)ST |
| 42 | 2.4 | 1 | (W)S(W)B(W) |
| 32 | 32 | 2 | TST |
| 40 | 12 | 2 | (W)STB(W) |
| 66 | 0.8 | 2 | (W)BB(W)B(W) |
|
| 图 8 结果显示 Fig. 8 Results visualizations |
在实用性方面,无论是在多模式组合情况,还是各种特殊评价标准权衡要求的情况下,该方法均能给出较为实用的出行方案,为出行信息服务从大众服务到个性化服务提供借鉴,并且适用于各种路径生成算法和方法改造。在效率方面,由于遗传算法具有很强的并行性,可以同时处理一个种群,即多个个体,可以采用诸如并行计算、分布式处理等方式提高效率。除了采用算法自身加速改造,如算法终止条件、路径生成加速算法、加速进化策略等,还可以采用并行遗传算法(parallel GA)提高效率。通过将串行算法并行化,采用一定的信息交互模型,如主从式模型、粗粒度模型、细粒度模型和混合模型等,实现本文方法的并行遗传算法改造,这在互联网地图服务大用户并发、分布式数据存储的情况下尤其适用。 4 结 论
本文提出了一种适宜多模式交通网络环境下的多标准路径搜索方法。该方法结合遗传算法与最优化理论,采用不定长表现型基因编码,使用模式标识表示不同模式下的路径。为了适应多模式交通网络环境,定义模式内交叉与变异算子和模式间交叉与变异算子,使遗传进化能够同时兼顾模式内与模式间不同的进化方向。采用多维权值向量表示多种评价标准,涉及时间最短、换乘最少和费用最低等标准。通过应用Pareto排序方法进行适应度值的分配。该方法能够有效避免人为设置权重值导致的多标准权衡偏差。通过对比试验确定了遗传算法进化参数的分配方案。试验结果显示,该方法能够实现更为多样的模式组合方式,同时兼顾不同程度的用户需求,为出行者提供满足个性化需求的、优化可替换的、无缝全程无障碍出行服务。在后续的研究中,需要进一步考虑该方法的效率改进方法以及实时路况对路径计算的影响,以提供更加符合用户出行需求的出行服务。
| [1] | MOONEY P, WINSTANLEY A. An Evolutionary Algorithm for Multicriteria Path Optimization Problems[J]. International Journal of Geographical Information Science, 2006, 20(4):401-423. |
| [2] | PEREIRA C M N A. Evolutionary Multicriteria Optimization in Core Designs: Basic Investigations and Case Study[J]. Annals of Nuclear Energy, 2004, 31(11):1251-1264. |
| [3] | LI R, LEUNG Y. Multi-Objective Route Planning for Dangerous Goods Using Compromise Programming[J]. Journal of Geographical Systems, 2011, 13(3):249-271. |
| [4] | CHAKRABORTY B. GA-based Multiple Route Selection for Car Navigation[M].Berlin: Springer-Verlag, 2004:76-83. |
| [5] | HUANG B, FERY P, XUE L, et al. Seeking the Pareto Front for Multiobjective Spatial Optimization Problems[J]. International Journal of Geographical Information Science, 2008, 22 (5):507-526. |
| [6] | MARTINS E Q V. On a Multicriteria Shortest Path Problem[J]. European Journal of Operational Research, 1984,16(2):236-245. |
| [7] | HANSEN P. Bicriterion Path Problems[C]//Multiple Criteria Decision Making: Theory and Application.[S.l.]:Springer-Verlag,1980: 109. |
| [8] | BRUMBAUGH S J, SHIER D. An Empirical Investigation of Some Bicriterion Shortest Path Algorithms[J]. European Journal of Operational Research, 1989, 43(2):216-224. |
| [9] | SKRIVER A J V, ANDERSEN K A. A Label Correcting Approach for Solving Bicriterion Shortest-path Problems[J]. Computers and Operations Research, 2000, 27(6):507-524. |
| [10] | LOZANO A, STORCHI G. Shortest Viable Path Algorithm in Multimodal Networks[J]. Transportation Research Part A: Policy and Practice, 2001, 35(3):225-241. |
| [11] | GEN M, CHENG R, WANG D. Genetic Algorithms for Solving Shortest Path Problems[C]//Proceedings of IEEE International Conference on Evolutionary Computation. Indianapolis:IEEE Press,1997:401-406. |
| [12] | INAGAKI J, HASEYAMA M, KITAJIMA H. A Genetic Algorithm for Determining Multiple Routes and Its Applications[C]// Proceedings of the 1999 IEEE International Symposium on Circuits and Systems.[S.l.]:IEEE, 1999:137-140. |
| [13] | SUN Huiwen. A Genetic Algorithm for Travelling Salesman Problems[J]. Journal of Southwest Jiaotong University, 1996, 31(5): 550-554. (孙惠文. 遗传算法求解旅行商问题[J]. 西南交通大学学报, 1996,31(5):550-554.) |
| [14] | MA Xuan. A Genetic Algorithm for k Optimal Paths Problem[J]. Computer Engineering and Applications, 2006(12) :100-101. (马炫. 求解k条最优路径问题的遗传算法[J]. 计算机工程与应用, 2006(12):100-101.) |
| [15] | JIANG Bo. Study of Vehicle Routing Problem with Time Windows Based on Genetic Algorithm[D]. Beijing: Beijing Jiaotong University, 2010. (蒋波. 基于遗传算法的带时间窗车辆路径优化问题研究[D]. 北京: 北京交通大学, 2010.) |
| [16] | LI Qing, ZHANG Wei, YIN Yixin, et al. An Improved Genetic Algorithm for Optimal Path Planning[J]. Information and Control, 2006, 35(4):444-447. (李擎, 张伟, 尹怡欣, 等. 一种用于最优路径规划的改进遗传算法[J]. 信息与控制, 2006, 35(4):444-447.) |
| [17] | HUANG Z D, LIU X J, HUANG C C, et al. A GIS-based Framework for Bus Network Optimization Using Genetic Algorithm[J]. Annals of GIS, 2010, 16(3):185-194. |
| [18] | LIU Xuhong, ZHANG Guoying, LIU Yushu, et al. Path Planning Based on Multi-objective Genetic Algorithm[J]. Transactions of Beijing Institute of Technology, 2005, 25(7):613-616. (刘旭红, 张国英, 刘玉树, 等. 基于多目标遗传算法的路径规划[J]. 北京理工大学学报, 2005, 25(7):613-616.) |
| [19] | ABDELGAWAD H, ABDULHAI B, WAHBA M. Multiobjective Optimization for Multimodal Evacuation[J]. Transportation Research Record: Journal of the Transportation Research Board, 2010, 2196:21-33. |
| [20] | ABBASPOUR R A, SAMADZADEGAN F. A Solution for Time-dependent Multimodal Shortest Path Problem[J]. Journal of Applied Sciences, 2009, 9(21):3804-3812. |
| [21] | ABBASPOUR R A, SAMADZADEGAN F. An Evolutionary Solution for Multimodal Shortest Path Problem in Metropolises[J]. Computer Science and Information Systems, 2010, 7(4): 789-811. |
| [22] | MICHALEWICZ Z. Genetic Algorithms+Data Structures=Evolution Programs[M]. Berlin: Springer-Verlag, 1996. |
| [23] | FONSECA C M, FLEMING P J. Genetic Algorithms for Multiobjective Optimization: Formulation, Discussion and Generalization[C]//Proceedings of the Fifth International Conference on Genetic Algorithms, University of Illinois at Urbana-Champaign.San Mateo:[s.n.],1993:416-423. |
| [24] | YU Haicong, LU Feng. A Multi-criteria Route Planning Approach Considering Walking Guidance[J]. Journal of Image and Graphics, 2010, 15(4):677-683. (于海璁, 陆锋. 一种顾及步行引导的多标准路径规划方法[J]. 中国图象图形学报, 2010,15(4):677-683.) |
| [25] | ZITZLER E, DEB K, THIELE L. Comparison of Multiobjective Evolutionary Algorithms: Empirical Results[J].Evolutionary Computation, 2000, 8(2):173-195. |