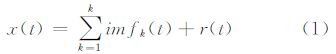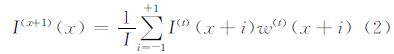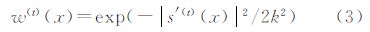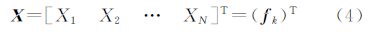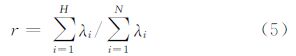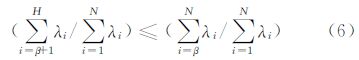2. 湖南城市学院 市政与测绘工程学院,湖南 益阳 41300
2. School of Municipal and Surveying Engineering, Hunan City University, Yiyang 413000, China
1 引 言
对干涉图进行相位解缠是干涉SAR数据处理过程中的一项重要工作。然而由于系统性热噪声、时间去相关、空间去相关、多普勒中心去相关以及大气和水蒸气等因素的影响等,使得干涉图常存在严重的噪声[1]。干涉图中噪声的存在,使得相位值偏离其真实值,进而影响到下一步相位解缠处理的精度,严重的甚至会造成相位解缠的失败,因此必须对干涉图相位进行滤波以降低噪声。目前,国内外学者提出许多干涉图去噪方法,其中具有代表性的如文献[2]提出的Goldstein滤波方法;文献[3, 4]提出的圆周期均值滤波和圆周期中值滤波方法;文献[5]提出的自适应滤波方法;文献[6]提出的等值线滤波方法;文献[7]基于相干性和文献[8]基于信噪比提出的改进的Goldstein滤波算法;以及文献[9]提出基于条纹中心线的InSAR干涉图滤波方法等。总的来说这些方法可以归纳为两类,即空间域滤波和频率域滤波。上述方法虽然在一定程度上抑制了部分噪声,但由于InSAR干涉数据有其本身的规律,一般简单的滤波平滑方法并不能达到理想的去噪效果。
近年来,部分学者提出了利用经验模态分解[10, 11](empirical mode decomposition,EMD)进行SAR干涉图噪声的抑制,为干涉图去噪提供了一种新的思路。其方法是将信号分解成有限个本征模函数分量IMF(intrinsic mode function)和一个趋势函数之和,它依据数据自身的时间尺度特征来进行信号分解,无须预先设定任何基函数和分解层数。在EMD噪声抑制算法中,大都是采用部分重构的方法进行去噪的[11, 12, 13, 14]。在前述的方法中,对EMD分解的前几项IMF认为全部由噪声构成,直接去除,对剩下的IMF进行累加重构,以达到去噪目的。然而含噪信号经EMD分解后,前几项IMF仍含有细节信息,后面几项的IMF也含有不同程度的噪声,如采用部分重构的方法将会损失大量细节信息,噪声也不能得到有效地抑制[15]。基于上述不足,本文对EMD去噪方法进行了改进,提出一种基于EMD-自适应滤波的干涉图相位噪声抑制方法。该方法首先对经干涉图变换的正弦图像和余弦图像进行EMD分解,然后根据干涉图的梯度来确定平滑模板内各像素的相位值对滤波后模板中心点像素相位值的贡献情况,对IMF中所含噪声实现低信噪比区域强滤波、高信噪比区域弱滤波,最后对处理后的IMF进行重构,得到去噪后的干涉相位图。试验结果表明,该方法不仅具有较强的噪声抑制能力,在噪声降低的同时较好地保持了干涉相位图的边缘和细节,有效地减少了信息的丢失。
2 EMD算法基本原理经验模态分解(empirical mode decomposition,EMD)是由文献[10]提出的一种适用于分析和处理非线性、非平稳随机信号的方法。该方法能够把一个复杂的非线性、非平稳的信号分解成若干线性、平稳的数据层,同时产生一个本征模函数分量(IMF)的集合,从而达到对信息分层处理的目的。本征模函数(IMF)必须同时满足以下两个条件:一是函数在整个时间范围内,局部极值点和过零点的数目必须相等,或最多相差一个;二是在任意时刻点,局部最大值的包络和局部最小值的包络的平均必须为0。于是对于任何一个信号就可以分解为有限个本征模函数IMF之和[16]。
EMD分解是基于以下假设条件:① 信号至少有两个极值,一个最大值和一个最小值;② 数据的局部时域特性是由极值间隔来确定的;③ 如果数据缺乏极值但是含有拐点,那么可以通过对数据微分一次或多次来求得极值点,然后再通过积分来获得分解的结果[16]。通过筛分过程(sifting process)将信号分解成一系列特征尺度由最小到最大依次增大的IMF和一个趋势项余量。其筛分过程如下。给定一个时间序列x(t),令r(t)=x(t),k=1,i=0,极值点个数阈值为n。
步骤1:找到r(t)的所有局部极大值和极小值。
步骤2:用样条插值法得到局部极大值和极小值的上下包络分别为cmax(t)和cmin(t)。
步骤3:由上下包络求出其平均值
m(t)=(cmax(t)+cmin(t))/2
步骤4:令i=i+1,提取PMF(proto-mode function),pi(t)=r(t)-m(t),r(t)=pi(t)。
步骤5:循环1~4步,直到pi(t)满足IMF的两个条件,则令imfk(t)=pi(t)。
步骤6:令r(t)=r(t)-imfk(t),如果r(t)极值点个数大于n,则令k=k+1,i=0并且回到步骤1,否则,结束筛分过程。经EMD分解的信号即表示为
式中,k为分解出的IMF的个数;r(t)为信号x(t) 的趋势项。
由上述步骤得到的本征模函数序列按尺度从小到大依次排列,图像中的斑点噪声成分包含在小尺度分量即高频分量中,去掉排列在前的1个或者2个小尺度分量,然后重构图像,这样就达到了滤除噪声的目的[18]。据此经验模态分解法可以有效地分离不同空间尺度的信息,处理非平稳、非线性的信息;空间-频率能把奇异信号对处理结果的污染控制在很小的范围内,使一点的异常振动只影响到局部,而不会扩散到整个区域。因此,用EMD方法可以对图像进行有效的尺度分离。
3 EMD-自适应滤波方法及实现 3.1 基于EMD-自适应滤波方法对于基于EMD 的时空尺度滤波,通常采用原始信号减去EMD分解的一个或多个IMF来进行滤波处理,这样虽然能去除部分噪声,但是会导致将所减去IMF里面包含的有用信号与噪声一起被滤掉,是一种简单和粗糙的滤波方法[17]。文献[18]研究表明,含噪信号经EMD分解后,前几项IMF中仍含有较多的细节信息,而且后面的IMF中也分布有不同程度的噪声,因此采用直接部分重构的方法对图像去噪,会损失大量的细节信息。基于以上分析,本文对EMD分解进行改进,提出一种基于EMD-自适应滤波方法。
该算法先将干涉条纹图转换为正弦图像和余弦图像,然后再进行EMD分解处理,这是因为干涉条纹图的相位在+π到-π处会出现突变,经过转换后,相位跳跃的问题得到解决[19];还有一种解决的办法是将干涉条纹图分解为实部和虚部两部分,然后再分别对实部和虚部进行EMD分解滤波(本文是采用的第一种方法);其次分别对前n个高频IMF按图像的梯度信息来进行自适应滤波处理;之后,将经过去噪了的IMF与没有经过去噪的IMF重构即到滤波后的干涉图。
设I0(x)为变换后的正弦图像和余弦图像(或者是干涉图的实部和虚部),w(x)是滤波窗口的函数,等权值窗口平滑滤波器则可表示
式中,I(x+1)(x)为第t+1 次迭代平滑后的信号;I=∑w(t)(x+i);对于等权平滑模板则有w(t)(x+i)=1。
利用式(2)对信号逐点进行等权平滑时,并没有考虑是否是边缘。然而在实际处理时变换的图像出现黑白相间条纹的可能性较大,这些边缘出现的地方一般为最终干涉条纹边缘出现的地方,因此在滤波时,需要同样保持好这些边缘信息[20]。
假定边缘处模板w(t)(x)中对应的权系数为0时,一般不进行平滑处理。然而在突变处所分隔开的两个不通区域的点,将不会同时被平均处理。另外对于突变处的点,在平滑处理过程中将其归入到其邻近所在的区域内,以增强其边缘;对突变位置的确定和判别,根据信号的梯度信息来进行判断。窗口权系数的定义如下[20]
式中,s′(t)(x)为信号s(t)(x)的一阶导数;k为尺度函数,其为确定保留下的边缘幅度信息。对上式作如下约定:假如该信号的梯度大于尺度函数k ,则认为该点处于边缘之上,边缘点所在的滤波窗口对应的权系数相应减小,从而使得边缘信息得以保留;相反,假如该信号的梯度小于尺度函数k,则对应于非边缘的点,其权系数就相应增大,在非边缘区域内的梯度低于尺度函数k窗口内各权系数接近,较大程度上参与平滑处理,同时将信号的不平坦区域平滑掉,以达到去除噪声的目的[20]。
3.2 IMF滤波个数的确定在利用自适应滤波去除IMF中的噪声时,关键是IMF个数的选择问题,IMF个数选择得过多,会损失较多的信号细节信息;选择得过少,则会残留较多的噪声,导致噪声不能有效去除[21]。为了选择合适的IMF个数进行滤波,本文引入principle component analysis(PCA)[22]来进行IMF个数的筛选。
设I0为干涉图经余弦或正弦变换的余弦图像或正弦图像,I0经过EMD分解后,第k层的IMF为imfk,为了方便讨论,令imfk=fk。记
则CX=E{(X-mX)(X-mX)T}为fk的协方差阵。设λ1≥λ2≥…λN是CX的特征值,φ1、φ2、…、φN是对应的特征向量,记Φ=[φ1 φ2 … φN]T,则Φ是一个正交矩阵向量。定义
Y=[Y1 Y2 … YN]T=Φ(X-mX)
由PCA特性可知,X中的噪声分布在所有的分量Yi中,而信号主要集中在前几层的成分分量中。设主成分的累计贡献率为
式中,N为IMF分解的个数,由r的大小来确定保留成分分量的个数,H为停止滤波的层数。而实际条件下,H很难选择,本文对H的选择按照下面来进行取值,即
如果存在β使得式(6)成立,则取H=β。
3.3 基于EMD-自适应滤波方法步骤设I是含有噪声的干涉图像,I′是去噪后的干涉图像,I0是I经变换的余弦图像或正弦图像,imfn是Isub>0通过EMD算法分解得到的n个固有模态函数,本文提出的基于EMD-自适应滤波方法进行干涉图去噪的步骤如下:
步骤1 对干涉图I分别进行正弦和余弦转换,生成正弦图像和余弦图像I0,即t1=sinφ,t1=cosφ,转换后,干涉图的相位值在[-π +π]之间。
步骤2 对正弦图像和余弦图像I0按照距离向和方位向分别进行EMD分解;分别得到正弦图像和余弦图像的固有模态函数imfns和固有模态函数imfnc。
步骤3 按照公式(6),分别选择前H个固有模态函数imfsH和imfHc进行自适应滤波处理,对滤波后的imfHs′和imfcH′及剩余趋势函数进行累加重构,得到滤波后的正弦图T1和余弦图T2。
步骤4 通过逆变换得到滤波后的干涉条纹图I′。
在IMF分解过程中,对极大值序列和极小值序列进行插值求其包络是其关键。在本文中,采用三次样条插值算法求其包络,因为三次样条插值可以保证插值函数的一阶导数光滑,二阶导数连续,获得更光滑的包络线。
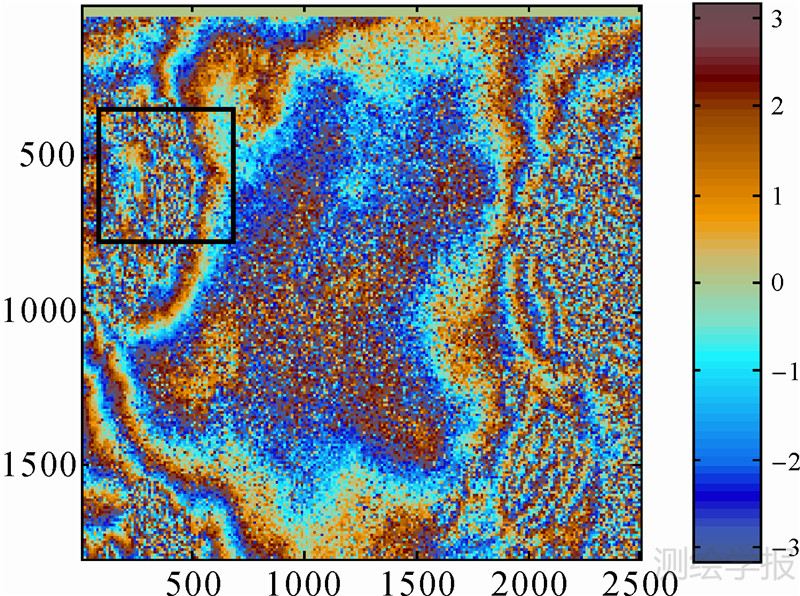
4 试验结果及分析 4.1 试验数据本文试验数据采用天津地区的间隔1 d的重复轨道ENVISAT-ASAR数据,大小为1800×2500,利用瑞士GAMMA软件进行预处理,去除平地效应,得到试验的干涉图(如图 1所示)。在图 1中选取一块500×500大小的具有代表性的区域(图 1)方框作为研究对象,并采用Goldstein滤波、圆周期中值滤波、自适应滤波、EMD分解方法和Baran滤波与本文方法进行分析比较。
|
| 图 1 天津地区干涉图( 矩形框区域为试验区) Fig. 1 An interferogram of Tianjin (the rectangular area is selected for experimental investigation) |
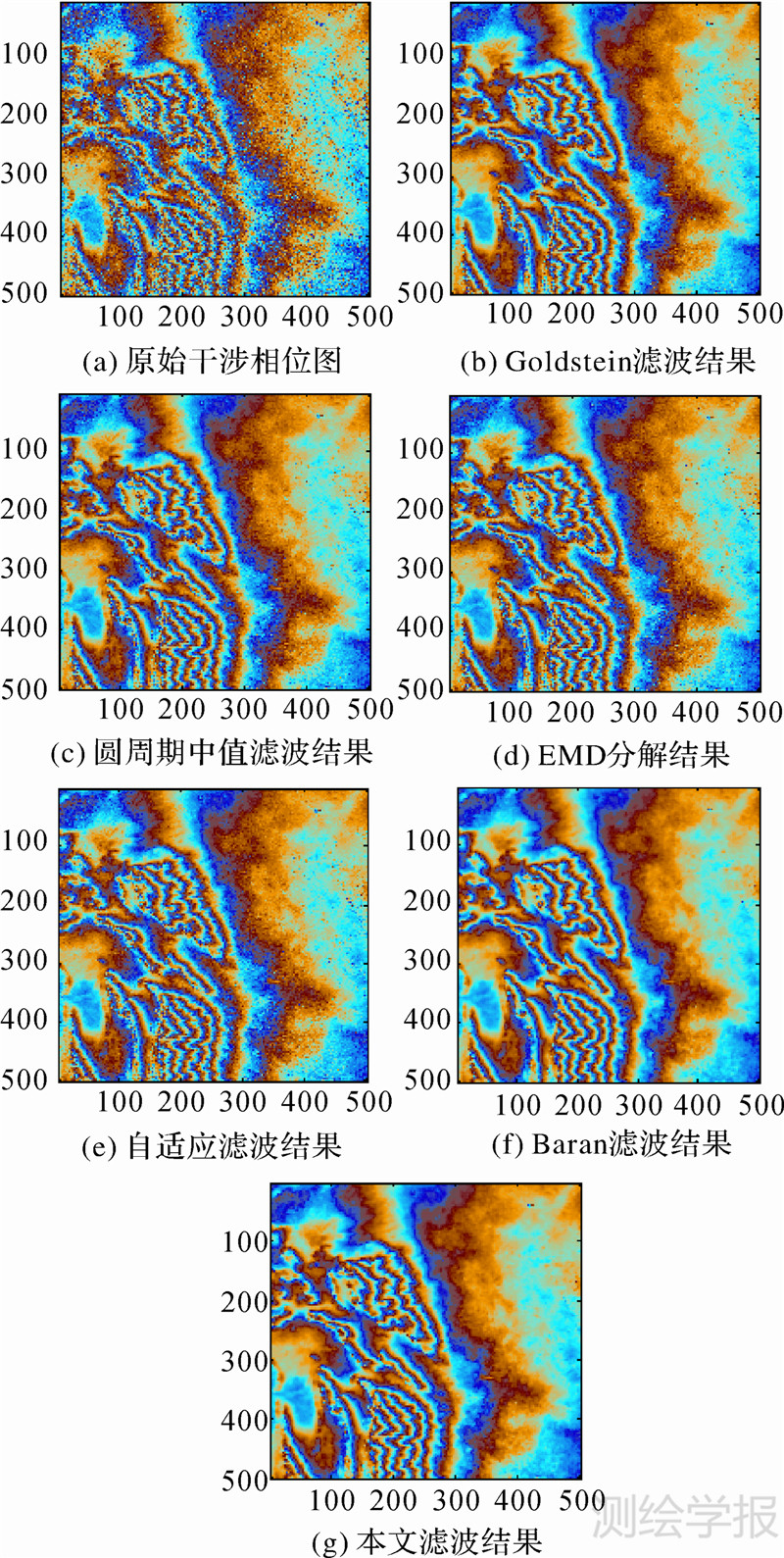
在进行滤波去噪时,Goldstein滤波的滤波参数α取值为0.5;EMD分解的IMF个数为三次滤波,即去除前3项IMF后,对余下分量进行重构;自适应滤波采用Lee滤波方法。几种滤波后的结果如图 2所示,图(a)表示为含噪声干涉图,图(b)~(g) 分别表示Goldstein滤波、圆周期中值滤波、EMD分解、Lee自适应滤波、Baran滤波和本文方法的滤波结果。由图(b)~(f),可以看出去噪后的干涉图像噪声斑点虽然大量减少,但是还有一些噪声的存在,个别地方出现条纹断裂,引入了小的虚假目标;从目视效果来看,EMD分解方法和圆周期中值滤波有很明显的斑点噪声未被消除;自适应滤波和Goldstein滤波虽然在一定程度上抑制了部分噪声,但是在条纹边缘处去噪效果不太明显。Baran滤波去噪效果要优于前4种滤波方法,但是条纹边缘的信息损失严重。在图(f)中,经整体图像平滑,没有明显噪声存在,噪声的抑制效果非常明显,与下文中真图的剖面图更为吻合,由此可见本文提出的滤波方法要优于前面4种滤波方法,特别是在条纹较密集的地方,较好地保持了条纹边缘信息。
|
| 图 2 各种滤波后的干涉图 Fig. 2 Interferogram filtered with different filters compared with original interferogram |
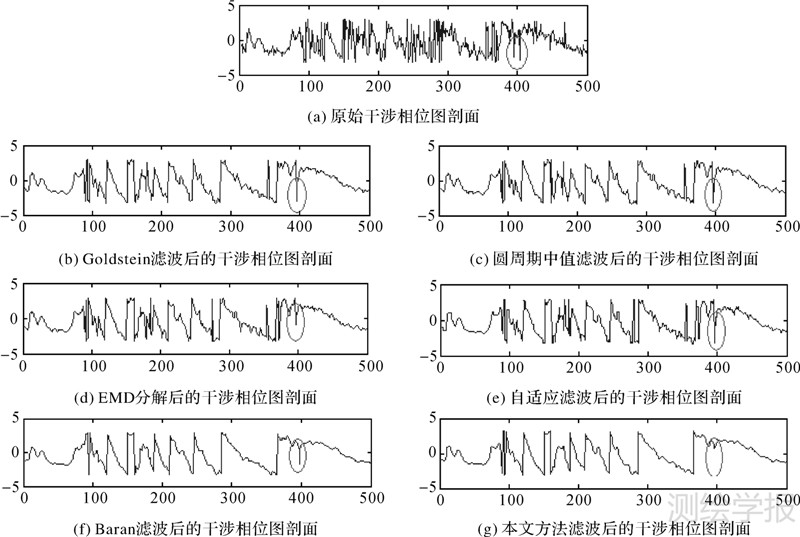
在含噪声的干涉图和滤波后的干涉图中,选取第375行的相位值进行进一步的比较研究,选取这行是因为其既有干涉条纹比较密集的区域,又有干涉条纹比较稀疏的区域,具有很强的代表性。其剖面图如图 3所示。
|
| 图 3 含噪声原始干涉图及各种滤波后的干涉图剖面(第273行) Fig. 3 Cross section over the filtered interferogram and original interferogram (row273) |
从图 3的剖面图可以看出,前5种滤波方法都对噪声起到了一定的平滑作用,但是还是有一些地方毛刺明显没有被去除,如图 3中(b)~(f)的圆圈处。另外从图 3(f) Baran滤波后的干涉相位图剖面还可以看出,相位的细节信息没有得到很好的保持,这也与图 2(f)Baran滤波结果相一致。与其他几种滤波器相比,本文方法滤波后的干涉图的条纹连续性更好,噪声的抑制效果非常明显(如图 3(g)的圆圈处),与真图的剖面图更为吻合,更好地保持了条纹的细节信息。
4.3 指标评价为了对滤波效果进行定量评价,本文选取了RMS指标[23]、相位标准差(PSD)[2]、相位差和值(SPD)[24]和边缘保持指数(EPI)[23]等几种干涉图滤波的定量评价指标对各种滤波方法进行评价。滤波后的干涉图的几种评价指标见表 1。
| 去噪方法 | RMS | PSD | SPD | EPI |
| 原始干涉图 | 2.973 5 | 5.8344E+005 | 5.8035E+005 | |
| Goldstein滤波 | 0.727 5 | 3.7682E+005 | 3.3822E+005 | 0.713 7 |
| 圆周期中值滤波 | 0.853 2 | 3.9453E+005 | 3.5872E+005 | 0.658 6 |
| EMD分解方法 | 0.843 9 | 4.7907E+005 | 4.4074E+005 | 0.604 7 |
| Lee自适应滤波 | 0.753 6 | 3.8763E+005 | 3.7974E+005 | 0.746 2 |
| Baran滤波 | 0.684 7 | 3.0145E+005 | 3.1523E+005 | 0.783 1 |
| 本文滤波方法 | 0.581 7 | 2.3457E+005 | 2.2621E+005 | 0.834 5 |
| 评价标准 | 越接近0越好 | 越小越好 | 越小越好 | 越接近1越好 |
从表 1的各项评价指标中可以看出,经过Goldstein滤波、圆周期中值滤波、EMD分解、自适应滤波和Baran滤波处理后,干涉图的RMS都有一定程度的降低,说明上述几种滤波方法对干涉图都起到了一定的平滑作用,本文方法的RMS最小,说明滤波效果最好;从其他几项指标也可知,本文方法的去噪能力明显优于其他几种方法,这也与图 2中滤波结果相吻合。从数据可得,本文算法对边缘和相位细节的保持方面要明显优于其他算法,这将有利于下一步的相位解缠工作。
4.4 平滑效果对相位解缠的影响衡量滤波的效果还要考虑到对相位解缠的影响,残余数(奇异点的个数)是其中的一个重要标准。在本文中采用枝切法来进行相位的解缠,并对各种方法解缠后的残余数[25]、枝切点数和孤立区[25]的数量进行比较分析。
图 4为滤波后相位解缠结果和残余图。从图 4(a)和(b)中可以看出,未滤波前有大量的孤立区(图中黑色块状区域)和很多的残余点数。经过滤波后,图 4(c)、(e)、(g)、(i)、(k)和(m)中孤立区得到减少,而图(m)中则几乎没有孤立区;图 4(d)、(f)、(h)、(j)、(l)和(n)中的残余点都了很明显减少,特别是图(n)中的残余点减少最为显著。从解缠的时间上看,去噪前干涉图、Goldstein滤波、圆周期中值滤波、EMD分解方法、自适应滤波和Baran滤波方法与本文方法滤波后的相位解缠所花的时间分别为97 s、62 s、63 s、84 s、57 s、53 s和49 s,由此可见,本文方法后的解缠时间比为滤波前的时间至少节约了一倍。

|
| 图 4 滤波后相位解缠结果和残余图对比结果 Fig. 4 Comparison of the phase unwrapping results and the residual graphs after filtering |
表 2为滤波前后的干涉相位图进行相位解缠后的枝切点数、孤立区和残余点数等数量的变化情况。从表 2可以看出,经过本文方法滤波后的干涉相位图的枝切点数、孤立区和残余点数的数量有了非常明显的减少,不能成功解缠的区域也是最少。这也证明了本文方法比其他几种滤波方法的优势所在。
| 去噪方法 | 枝切点数 | 孤立区数 | 残余点数 |
| 原始干涉图 | 234 731 | 51 236 | 398 337 |
| Goldstein滤波 | 5 063 | 514 | 4 147 |
| 圆周期中值滤波 | 5 372 | 536 | 6 653 |
| EMD分解方法 | 6 107 | 593 | 5 389 |
| Lee自适应滤波 | 4 216 | 512 | 4 734 |
| Baran滤波 | 3 874 | 374 | 2 693 |
| 本文滤波方法 | 2 971 | 204 | 1 767 |
| 评价标准 | 越少越好 | 越少越好 | 越少越好 |
经验模态分解是一种具有较强适应性的时频分析方法,基于EMD 的特性,本文提出了基于EMD-自适应滤波算法对干涉相位图进行了滤波,试验结果表明,无论从目视解译,还是定量的指标评价,该方法在去噪和边缘、细节保持方面均达到了比较好的效果,抑制相位噪声能力要优于前几种经典的滤波方法,将基于EMD-自适应滤波方法引用到抑制干涉图像噪声中是切实可行的。
| [1] | LIN Hui, ZHAO Changsheng, DU Peijun, et al. Research on Filtering Methods of InSAR Interferogram[J]. Acta Geodaetica et Cartographica Sinica,2005,34(2):113-117.(林卉,赵长胜,杜培军,等. InSAR干涉图滤波方法研究[J]. 测绘学报,2005,34(2):113-117.) |
| [2] | GOLDSTEIN R M, WEMER C L. Radar Interferogram Filtering for Geophysical Applications [J]. Geophysical Research Letters, 1998, 25(21): 4035- 4038. |
| [3] | EICHEL P H, GHIGLIA D C. Spotlight SAR Interferometry for Terrain Elevation Mapping and Interferometric Change Detection[R]. Sand: Sandia National Labs Technology, 1993: 2529-2546. |
| [4] | LANARI R, FORNARO G. Generation of Digital Elevation Models by Using SIR_C/X_SAR Multifrequency Two-pass Interferometry: The Etna Case Study[J]. IEEE Transaction on GRS, 1996, 34(5):1096-1115. |
| [5] | LEE J S, PAPATHANNASSION K P. A New Technique for Noise Filtering of SAR Interferometric Phase Images[J]. IEEE Transaction on GRS, 1998,36(6): 1455-1459. |
| [6] | YU Qifeng, FU Sihua. The Method of ESPI and InSAR Interference Based on Fringe Orientation and Fringe Contour[M]. Beijing: The Science Press, 2007.(于起峰,伏思华. 基于条纹方向和条纹等值线的ESPI与InSAR干涉条纹图处理方法[M].北京:科学出版社,2007.) |
| [7] | BARAN I, STEWART M P, KAMPES B M, et al. A Modification to the Goldstein Radar Interferogram Filter[J].IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(9):2114-2118. |
| [8] | SUN Qian, ZHU Jianjun, LI Zhiwei, et al. A New Adaptive InSAR Interferogram Filter Based on SNR[J].Acta Geodaetica et Cartographica Sinica,2009,38(5):437-449.(孙倩,朱建军,李志伟,等.基于信噪比的InSAR干涉图自适应滤波[J].测绘学报,2009,38(5):437-449.) |
| [9] | WANG Yaonan, PENG Shurong, DENG Jiwei, et al. InSAR Interferogram Filtering Based on the Center Lines of the Interference-stripes[J]. Acta Geodaetica et Cartographica Sinica,2009,38(3):210-215.(王耀南,彭曙蓉,邓积微,等.一种基于条纹中心线的InSAR干涉图滤波方法[J].测绘学报,2009,38(3):210-215.) |
| [10] | HUANG N E, SHEN Z, LONG S R. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear Non-stationary Time Series Analysis[J]. The Royal Society , 1998, 454:903-995. |
| [11] | YUE Huanyin, GUO Huadong, HAN Chunming, et al. A SAR Interferogram Filter Based on the Empirical Mode Decomposition Method[J]. Chinese High Technology Letters, 2001,12(6):37-40.(岳焕印,郭华东,韩春明,等.经验模态分解技术在SAR干涉图滤波中的应用[J].高技术通讯,2001,12(6):37-40.) |
| [12] | BERNINI B, GALIZZI E, FEDERICO A, et al. Evaluation of the 1D Empirical Mode Decomposition Method to Smooth Digital Speckle Pattern Interferometry Fringes[J].Optics and Lasers in Engineering, 2007, 45(3):723-729. |
| [13] | YUE Huanyin, GUO Huadong, HAN Chunming, et al. Phase Unwrapping of Noisy SAR Interferograms [J]. Acta Geodaetica et Cartographica Sinica, 2002,31 (2): 151-156. (岳焕印,郭华东,韩春明,等.噪声条件下的干涉SAR相位解缠[J].测绘学报,2002,31(2):151-156.) |
| [14] | FENG Zhou, XING Mengdao, BAI Xueru, et al. Narrow Band Interference Suppression for SAR Based on Complex Empirical Mode Decomposition [J].IEEE Geoscience and Remote Sensing Letters, 2009,6 (3):423-427. |
| [15] | TAN Shanwen, QIN Shuren, TANG Baoping. Hilbert-Huang Transforms Filter and Its Application [J]. Journal of Chongqing University, 2004.27 (2): 109-120.(谭善文,秦树人,汤宝平.Hilbert-Huang 变换的滤波特性及其应用[J].重庆大学学报,2004,27(2):109-120.) |
| [16] | HUANG Chengti. Hilbert-Huang Transform and Its Application[D].Chengdu: Southwest Jiaotong University, 2006. (黄诚惕.希尔伯特—黄变换及其应用研究[D].成都:西南交通大学,2006.) |
| [17] | KONG Guojie, ZHANG Peilin, XU Longtang, et al. Adaptive Filter Algorithm Based on Empirical Mode Decomposition and Its Application[J]. Signal Processing, 2009, 25(6):958-962. (孔国杰,张培林,徐龙堂等.基于经验模态分解的自适应滤波算法及其应用[J].信号处理,2009,25(6):958-962.) |
| [18] | KOPSINIS Y, MCLAUGHLI S. Development of EMD Based Denoising Methods Inspired by Wavelet Thresholding[J].IEEE Transactions on Signal Processing, 2009, 57(4):1351-1362. |
| [19] | WANG Zhiyong, ZHANG Jixian, HUANG Guomian. The Research on Filtering of the Phase Noise Filtering in the Interferometric SAR[J]. Science of Surveying and Mapping,2004,29(6):31-34.(王志勇,张继贤,黄国满.InSAR干涉条纹图去噪方法的研究[J].测绘科学,2004,29(6):31-34.) |
| [20] | LIAO Mingsheng, LIN Hui, ZHANG Zuxun, et al. Adaptive A1gorithm for Filtering Interferometric Phase Noise [J]. Journal of Remote Sensing, 2003,7(2):98-105.(廖明生,林晖,张祖勋,等.INSAR 干涉条纹图的复数空间自适应滤波[J].遥感学报,2003,7(2):98-105.) |
| [21] | WANG Wenbo, ZHAO Pan, ZHANG Xiaodong. Research on SAR Image Speckle Reduction Using EMD and Principal Component Analysis[J]. Acta Geodaetica et Cartographica Sinica,2012,41(6): 838-843.(王文波,赵攀,张晓东.利用经验模态分解和主成分分析的SAR图像相干斑抑制[J].测绘学报,2012,41 (6):838-843.) |
| [22] | ZHANG Lei, RASTISLAV L, WU Xiaolin. PCA Based Spatially Adaptive Denoising of CFA Images for Single Sensor Digital Cameras [J].IEEE Transactions on Image Processing, 2009, 18(4):797-812. |
| [23] | HAN Chunming, GUO Huadong, WANG Changlin, et al. The Essence of SAR Image Speckle Suppression[J]. Journal of Remote Sensing, 2002,6(6) :470-474. (韩春明,郭华东,王长林,等.SAR图像斑点噪声抑制的本质[J].遥感学报,2002,6(6):470-474.) |
| [24] | LI Zhilin, ZOU Weibao, DING Xiaoli, et al. A Quantitative Measure for the Quality of InSAR Interferograms Based on Phase Differences [J]. Photogrammetric Engineering and Remote Sensing, 2004, 70(10): 1131-1137. |
| [25] | LEE J S, JURKEVICHI. Speckle Filtering of Synthetic Aperture Radar Images: a Review [J]. Remote Sensing Reviews, 2007, 23(8):313-340. |