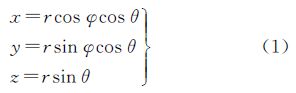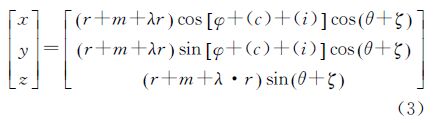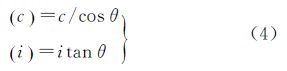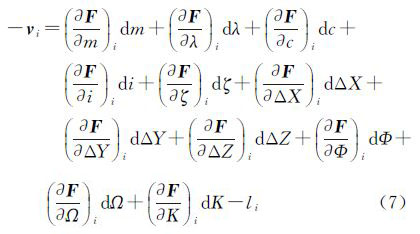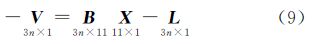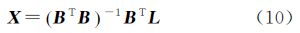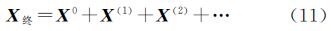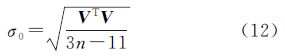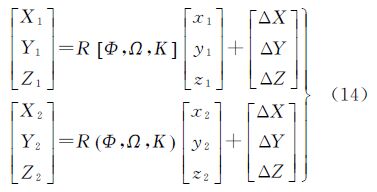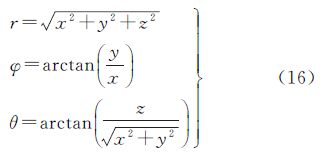2. 同济大学 测绘与地理信息学院,上海 200092;
3. 南昌工程学院 水利工程系,江西 南昌 330099
2. School of Surveying and Geo-Informatics, Tongji University, Shanghai 200092, China;
3. Department of Water Conservancy Engineering, Nanchang Institute of Technology, Nanchang 330099, China
地面激光扫描技术,也称“实景复制”技术,是一种新型的空间数据获取技术。同传统的测量手段相比,该技术具有数据获取速度快,实时性强,数据量大,主动性强,能全天候工作,全数字特征,信息传输、加工、表达容易,操作方便等优点[1],正受到越来越多科技工作者的关注。另一方面,由于激光扫描仪出现时间较晚,结构复杂,还没有统一的检定标准与规范,导致无法对其数据质量实施有效控制,不能发挥此类仪器应有的作用。但随着激光、计算机等技术的不断提高,此类仪器的价格在不断下降,越来越多的领域希望能使用这一高新仪器,因此有必要对仪器误差进行分析,以判断其是否能应用于高精度项目,如精密工程测量、高精度变形监测等领域。
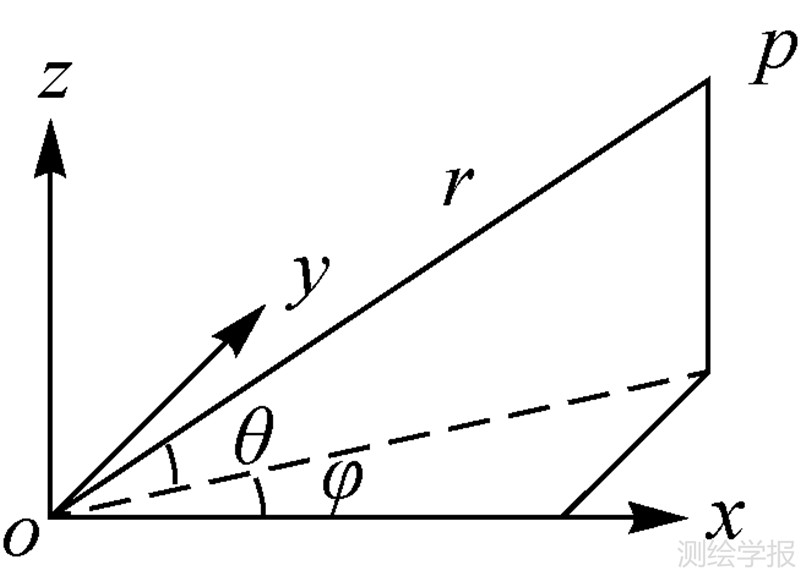
地面激光扫描仪采用扫描仪内部坐标系,其坐标原点位于扫描仪中心,通过主动发射激光对物体表面进行扫描,测量每个扫描点在扫描仪坐标系的球面坐标(r,φ,θ),如图 1所示。
|
| 图 1 扫描仪球面坐标系统 Fig. 1 Spherical coordinates system of laser scanner |
由图 1可得扫描点在仪器坐标系下的笛卡儿直角坐标系坐标(x,y,z)[2]
自2000年以来,地面激光扫描仪被引入测绘领域,其数据的准确度、精度问题及仪器的检校成为关注的焦点,研究人员展开了大量的研究工作。文献[3]从距离、色彩、入射角、目标材质等几方面研究影响激光扫描仪性能的因素。德国Mainze应用技术大学从2003年开始,从距离、角度分辨率、物体反射率、材质、边缘效应等方面对Callidus、Cyrax2500、S25、GS100、LMS-Z210、LMS-Z420i、Imager5003等多台仪器进行检定,结果表明在某些情况下,精度与厂家提供的有偏差[4]。为了验证地面激光扫描仪厂家给出的测量指标,2003年6月,美国国家标准与技术研究所在马里兰州盖瑟斯堡召集举办了LiDAR(light detection and ranging)检校研讨会,目的在于讨论与分享当前关于LiDAR检校的成果,确定性能评估及试验所需要的方案,确定检校实验室所需要的物质条件,开发LiDAR实验场可行计划,建立激光扫描仪检校标准[5]。文献[6]通过试验对StreetMapper移动地面三维激光扫描系统数据质量进行评估,得到了该系统扫描点平面坐标与高程值的准确度和精度。地面激光扫描仪在本世纪初引入中国,国内在此方面的研究也逐步展开。文献[7]对影响三维激光扫描仪测量误差的因素进行了理论分析。文献[8]评定了Riegl LMS-Q140i-80型激光扫描仪的精度,结果表明实际精度与标称精度一致。文献[9]分析了影响激光扫描仪距离测量的因素,并对国产RA-360激光扫描仪距离测量参数进行了标定。文献[10]则分析了RA-360激光扫描仪角度测量误差来源,并建立了该激光扫描仪角度测量误差检校模型。文献[11]分析了车载式激光扫描系统扫描点的误差来源,对系统扫描点的理论精度进行了评定。文献[12]通过试验确定了Leica ScanStation2型扫描仪的点位精度。文献[13]对车载扫描系统的相机内参数进行了标定,以实现激光扫描数据与线阵相机影像的精确对准。这些研究主要关注激光扫描仪的测量精度与性能。
近年来,有学者开始研究利用自检校法对仪器系统误差进行检定。文献[14]在假设地面激光扫描仪系统误差类型与全站仪类似的情况下,提出了扫描仪检校模型的概念,以确定扫描仪3个轴系间的平移量、旋转角及仪器的加、乘常数等9个参数,并对柏林技术大学开发的扫描仪原型机进行了检校。文献[15]利用经纬仪误差模型,提出了一个附加七参数模型及三维自由网自检校过程,并对Faro 880激光扫描仪进行了检校。文献[16]又对以前构建的误差模型进行了完善,重新构建了19个附加参数的数学模型。文献[17] 也根据经纬仪误差模型对Z+F imager 5003进行了检校,估计仪器的瞄准轴误差、水平轴误差及竖角指标差。瑞典皇家技术学院(KTH)大地测量部门专门建立了一个室内检校场,构建了包含10个参数的扫描仪自检校模型,并对Callidus1.1、Leica HDS 3000及Leica HDS 2500等3种仪器进行研究,得出了有关仪器的测距误差、水平角误差及垂直角误差[18]。文献[19]对地面激光扫描仪自检校附加参数的稳定性进行分析文献[20]分析了机载LiDAR系统安置误差对定位精度的影响,利用自检校法确定了GPS、激光扫描仪、惯性导航单元三者之间安置参数的误差。到目前为止,对于自检校法中参数并没有统一的标准。
本文在文献[16, 18]的基础上,以空间相似变换公式为基础,构建了一个包含11个参数的自检校误差模型,其中6个外部定向参数,5个仪器系统误差参数,并详细推导了计算公式。为了验正误差模型的正确性,以HDS3000为试验对象,利用此误差模型求解该仪器的系统误差值并对其观测结果进行改正。
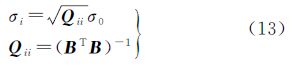
2 系统误差标定自检校法的基本思路是将观测数据中可能存在的系统误差通过某种误差模型,以参数形式表示,并将这些附加参数作为未知数经过统一平差解算出来[21]。
2.1 自检校法公式推导
自检校法中包含两类参数,一类是扫描仪坐标系与外部坐标系的转换参数,称为外部定向参数,包含3个平移参数及3个旋转参数;第二类是仪器系统误差参数。从操作原理上看,地面三维激光扫描仪可以看作是一台高速动态测角(水平角和垂直角)、无合作目标测距的高性能全站仪,因此可参考全站仪的误差来源,确定扫描仪中存在的系统误差,即设扫描仪存在的系统误差包括测距加常数m、测距乘常数λ、瞄准轴误差c、水平轴误差i及竖角指标差ζ,这样扫描仪的系统误差参数共有5个。自检校法的数学模型为
式中,X,Y,Z和x,y,z分别为点在外部坐标系下的坐标及在扫描仪坐标系下的坐标;ΔX,ΔY,ΔZ为扫描仪坐标系原点在外部坐标系下的坐标,即3个平移量;R为旋转矩阵,由3个旋转参数Φ,Ω,Κ构成。根据式(1),考虑到扫描仪存在的系统误差,扫描点在扫描仪下的坐标可表示为
式中,(c)、(i)分别为瞄准轴误差c,水平轴误差i对水平角的影响。参考全站仪的轴系误差,有[22] 将式(2)线性化,利用泰勒级数展开,取一次项,得到 式中 将外部坐标系下的量测值作为基准值,考虑到扫描仪观测值中存在的误差,可列出误差方程式 式中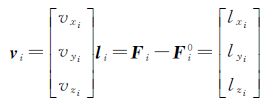
X=[dm dλ dc di dζ dΦ dΩ dΚ dX dΔY dΔZ]T
利用间接平差解算,得到未知数的改正数为 由于经过了线性化,因此解算时须采用迭代计算方法,直到未知数的改正数小于某一阈值为止。未知数的最终值为 单位权中误差为 各未知数的中误差为 2.2 未知数初始值的确定
由于采用线性化,因此需要确定未知参数的初始值。对于仪器系统误差而言,可以假定厂商在仪器制造时尽可能消除了各种误差,因此系统误差初始值可全部设为0;对于外定向参数,则取决于扫描仪的结构。当扫描仪具有对中、整平功能时,外定向参数的初值比较好确定,即角元素可以设为零,而平移参数可以通过全站仪测量得到;当扫描仪不具备对中、整平功能时,可以通过如下方法确定外定向初始值。
任意选取两对同名点(X1,Y1,Z1)、(x1,y1,z1)和(X2,Y2,Z2)、(x2,y2,z2),其均满足方程(2),即
两式相减,得
根据正交矩阵的特性及公式(15)解算出3个角元素Φ、Ω、Κ后,将其代入式(14)中任意一式,即可求出平移量ΔX,ΔY,ΔZ,将其作为外定向参数的初始值。
2.3 参数验证求出各参数后,必须验证其准确性。基本思路为:首先将验证点的扫描坐标按式(16)转换成原始观测值r、φ、θ,再利用检校参数根据公式(3)对原始观测值进行改正,计算改正后的验证点扫描坐标;最后利用外部定向参数将改正后的验证点扫描坐标转换至全站仪坐标系下,并与外部坐标系实测数据进行比较,计算出验证点的点位中误差。
3 试验及结果 3.1 数据获取为了验证模型的可行性与正确性,以徕卡HDS3000为试验对象进行仪器系统误差标定。在某教室布设了8个标靶,其中5个法如球标靶,3个徕卡旋转平面标靶,如图 2、图 3所示。用徕卡HDS3000对试验场景进行扫描,获取扫描数据。该款扫描仪具有粗略对中、整平功能。外部坐标系利用索佳NET1200全站仪建立。HDS3000激光扫描仪本身没有人工目视照准功能,也不能进行人工控制单点(特定目标点)测量,试验借助标靶,以提高点识别的精度。将拟合出的靶心扫描坐标与全站仪实测坐标作为同名点,用来确定外定向参数与仪器系统误差。

|
| 图 2 试验场景图 Fig. 2 Experiment scene |

|
| 图 3 标靶示意图 Fig. 3 Targets used in experiment |
利用全站仪和扫描仪分别获取8个标靶在两套坐标系下的坐标,见表 1。
| m | |||||||
| 目标 | 全站仪实测坐标 | 扫描坐标 | |||||
| X | Y | Z | X | Y | Z | ||
| 球1 | 6.536 8 | 10.022 4 | 5.707 1 | 3.805 7 | -3.613 2 | -0.495 7 | |
| 球2 | 2.783 0 | 11.252 1 | 5.562 8 | 1.143 7 | -6.527 5 | -0.650 2 | |
| 球3 | 2.804 1 | 7.596 4 | 5.564 0 | -0.632 5 | -3.333 1 | -0.642 9 | |
| 球4 | 0.465 9 | 6.798 9 | 5.177 5 | -3.058 0 | -3.787 8 | -1.033 2 | |
| 球5 | 1.150 9 | 4.862 3 | 5.561 1 | -3.411 9 | -1.767 3 | -0.645 1 | |
| 平面1 | 4.681 3 | 8.946 7 | 5.629 2 | 1.661 3 | -3.585 6 | -0.575 6 | |
| 平面2 | 4.888 8 | 6.742 9 | 5.655 5 | 0.759 3 | -1.564 8 | -0.544 7 | |
| 平面3 | 3.001 3 | 5.023 2 | 5.631 4 | -1.722 4 | -0.995 4 | -0.568 9 | |
当不考虑仪器中存在的系统误差时,利用5个球标靶的扫描坐标及全站仪实测坐标,解算出外定向参数,得
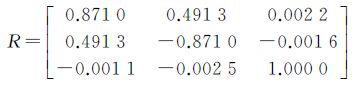
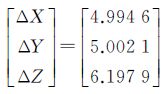
通过外定向参数,将3个平面标靶的扫描坐标转换至全站仪坐标系下,并与实测坐标相比较,结果见表 2。
| m | |||||||||||
| 目标 | 转换后坐标 | 全站仪实测坐标 | 坐标差 | ||||||||
| X | Y | Z | X | Y | Z | δX | δY | δZ | |||
| 平面1 | 4.678 6 | 8.942 2 | 5.629 4 | 4.681 3 | 8.946 7 | 5.629 2 | -0.002 7 | -0.004 5 | 0.000 2 | ||
| 平面2 | 4.885 9 | 6.738 9 | 5.656 2 | 4.888 8 | 6.742 9 | 5.655 5 | -0.002 9 | -0.004 0 | 0.000 7 | ||
| 平面3 | 3.004 1 | 5.023 8 | 5.633 5 | 3.001 3 | 5.023 2 | 5.631 4 | 0.002 8 | 0.000 6 | 0.002 1 | ||
各方向误差为

点位中误差
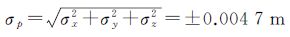
采用5个球标靶的两套坐标,根据式(5)—式(11)求解出外部定向参数及仪器系统误差,见表 3。
| 仪器系统误差 | 外部定向参数 | ||
| 旋转矩阵 | 平移矩阵/m | ||
| 加常数m/m | 0.006 1 | 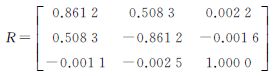 |  |
| 乘常数λ | -1.217 0E-004 | ||
| 瞄准轴误差c/rad | 0.019 7 | ||
| 水平轴误差i/rad | 0.002 9 | ||
| 垂直角误差ζ/rad | -9.720 3E-005 | ||
利用上面解算出来的仪器系统误差参数,对平面标靶的坐标进行改正,再利用外部定向参数转换至全站仪坐标系下,得到实测坐标与转换坐标的差值,结果见表 4。
| m | |||||||||||
| 目标 | 经改正、转换后坐标 | 全站仪实测坐标 | 坐标差 | ||||||||
| X | Y | Z | X | Y | Z | δX | δY | δZ | |||
| 平面1 | 4.680 7 | 8.944 7 | 5.629 5 | 4.681 3 | 8.946 7 | 5.629 2 | -0.000 6 | -0.002 0 | 0.000 3 | ||
| 平面2 | 4.889 0 | 6.741 1 | 5.655 8 | 4.888 8 | 6.742 9 | 5.655 5 | 0.000 2 | -0.001 8 | 0.000 3 | ||
| 平面3 | 3.002 0 | 5.021 0 | 5.633 0 | 3.001 3 | 5.023 2 | 5.631 4 | 0.000 7 | -0.002 2 | 0.001 6 | ||
各方向误差为
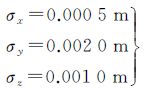
点位中误差
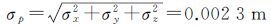
表 5反映了仪器系统误差改正前后点位精度比较。
| 名称 | 改正前/mm | 改正后/mm | 精度提高/(%) |
| x方向误差 | 2.8 | 0.5 | 82.1 |
| y方向误差 | 3.5 | 2.0 | 42.9 |
| z方向误差 | 1.3 | 1.0 | 23.1 |
| 点位精度 | 4.7 | 2.3 | 51.1 |
通过比较可知,经过仪器系统误差改正后,检验点各方向误差均较改正前有所提高,同时点位中误差由改正前的4.7 mm提高到2.3 mm,精度提高约51%。
4 结 语本文在假设扫描仪具有与全站仪相同系统误差来源的前提下,构建了具有11个参数的扫描仪自检校误差模型,推导了具体的计算公式,并利用所建误差检校模型,对HDS3000扫描仪进行了检校。结果证明经过系统误差改正后,数据质量有所提高。随着技术的不断发展,长距离地面激光扫描仪也逐步出现,本文尝试将测距乘常数作为自检校法中的一个参数,可使检校仪器的范围更加广泛。
在参数解算过程中,参数之间存在的相关性使得采用间接平差进行解算未必能获得最佳结果,因此对参数间的相关性进行分析,以找到弱化或消除参数相关的方法,从而提高参数解算精度是下一步的研究内容。此外,研究所确定的检定参数是否具有稳定性,能否针对不同场景获取的点云数据进行改正,也是接下来要进一步研究的工作。
| [1] | LI Bijun, FANG Zhixiang, REN Juan. Extraction of Building’s Feature from Laser Scanning Data[J].Geomatics and Information Science of Wuhan University, 2003, 28(1): 65-70.(李必军,方志祥,任娟. 从激光扫描数据中进行建筑物特征提取研究[J]. 武汉大学学报: 信息科学版,2003,28(1):65-70.) |
| [2] | PFEIFER N, BRIESE C. Laser Scanning-principles and Applications Summary[DB/OL]. 2008-1-18[2012-05-21] http://publik.tuwien.ac.at/files/pub-geo_1951.pdf. |
| [3] | CHEOK G S, LEIGH S D, RUKHIN A R. Calibration Experiments of a Laser Scanner[EB/OL]. Washington: NISTIR, 2002[2013-12-19]. http://www.nist.gov/manuscript-publication-search.cfm?pub_id=860455 |
| [4] | BOEHLER W, MARBS A. Investigating Laser Scanner Accuracy [DB/OL]. 2006-11-16[2012-4-13]. http://scanning. fh-mainz.de/scannertest/results300305.pdf |
| [5] | CHEOK G S. Proceedings of the LADAR Calibration Facility Workshop[M]. Gaithersburg: NISTIR, 2003. |
| [6] | BARBER D, MILLS J, SMITH-VOYSEY S. Geometric Validation of a Ground-based Mobile Laser Scanning System[J]. ISPRS Journal of Photogrammetry&Remote Sensing,2008, 63(1):128-141. |
| [7] | ZHENG Dehua, SHENG Yunzhong, LIU Chun. 3D Laser Scanner and Its Effect Factor Analysis of Surveying Error [J]. Engineering of Surveying and Mapping, 2005, 14(2): 32-34. (郑德华,沈云中,刘春. 三维激光扫描仪及其测量误差影响因素分析[J]. 测绘工程,2005,14(2):32-34.) |
| [8] | WANG Dong, LU Xiushan, ZHANG Zhanjie. Precision Evaluation of RIEGL LMS-Q140i-80 Laser Scanner[J]. Surveying and Mapping Science, 2006, 31(5): 115-116. (王冬,卢秀山,张占杰. Riegl LMS-Q140i-80型激光扫描仪精度评定[J]. 测绘科学, 2006, 31(5): 115-116.) |
| [9] | WANG Liuzhao, HAN Youmei, ZHONG Ruofei. The Range Calibration of the Vehicular Laser Scanner[J]. Bulletin of Surveying and Mapping, 2010(1): 19-20. (王留召, 韩友美, 钟若飞. 车载激光扫描仪距离测量参数标定[J]. 测绘通报,2010(1): 19-20.) |
| [10] | HAN Youmei, WANG Liuzhao, LU Xiushan. Angle Error Calibration of 360° Laser Scanner[J]. Geotechnical Investigation & Surveying, 2011(2): 59-63. (韩友美, 王留召, 卢秀山. 360°激光扫描仪的测角误差检校研究[J]. 工程勘察,2011(2): 59-63.) |
| [11] | LU Xiushan, ZHENG Zuoya, WANG Dong, et al. Evaluating on Theoretical Accuracy of 3Dsurs System Scanner Point[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(2): 202-206. (卢秀山,郑作亚,王冬, 等. 3Dsurs系统激光扫描点的理论精度评定[J]. 测绘学报,2010,39(2): 202-206.) |
| [12] | WANG Yupeng, LU Xiaoping, GE Xiaotian, et al. Point Precision Assessment for Terrestrial 3D Laser Scanning [J]. Bulletin of Surveying and Mapping, 2011, (4): 10-13. (王玉鹏,卢小平,葛晓天, 等. 地面三维激光扫描点位精度评定[J]. 测绘通报,2011(4): 10-13.) |
| [13] | HAN Youmei, WANG Liuzhao, ZHHONG Ruofei. The Calibration of the Line Scan Camera Based on Laser Scanner[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(6): 631-635. (韩友美,王留召,钟若飞. 基于激光扫描仪的线阵相机动态高精度标定[J]. 测绘学报, 2010, 39(6): 631-635.) |
| [14] | GIELSDORF F, RIETDORF A, GRUENDIG L. A Concept for the Calibration of Terrestrial Laser Scanners: TS26 Positioning and Measurement Technologies and Practices II-laser Scanning and Photogrammetry[R]. FIG Working Week. Athens: FIG, 2004: 1-10. |
| [15] | LICHTI D D, FRANKE J. Self-calibration of the iQsun 880 Laser Scanner[R]. Optical 3-D Measurement Techniques VII. Vienna: [s.n.], 2005: 112-121. |
| [16] | LICHTI D D, LICHT M G. Experiences with Terrestrial Laser Scanner Modelling and Accuracy Assessment[C]//Proceedings of the ISPRS Commission V Symposium: Image Engineering and Vision Metrology: XXXVI. Dresden: ISPRS, 2006: 155-160. |
| [17] | ABMAYR T, DALTON G, HTRL F, et al. Standardization and Visualization of 2.5D Scanning Data and Color Information by Inverse Mapping[C]// Proceedings of 7th Conference on Optical 3-D Measurement Techniques. Vienna: [s.n.], 2005: 164-173. |
| [18] | RESHETYUK Y. Calibration of Terrestrial Laser Scanners for the Purpose of Geodetic Engineering[R]. 3rd IAG/12th FIG Symposium. Baden: [s.n.], 2006. |
| [19] | LICHTI D D. A Method to Test Differences between Additional Parameters Sets with a Case Study in Terrestrial Laser Scanner Self-calibration Stability Analysis[J]. ISPRS Journal of Photogrammetry&Remote Sensing, 2008, 63(2):169-180. |
| [20] | ZHANG Jing, JIANG Wanshou. Self-calibration of LiDAR System Mounting Biases Using Virtual Tie Point Model[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 762-769. (张靖,江万寿. 基于虚拟连接点模型的机载LiDAR系统安置误差自检校[J]. 测绘学报, 2011, 40(6): 762-769.) |
| [21] | ZHU Zhaoguang, SUN Hu, CUI Bingguang. Photogrammetry[M]. Beijing: Surveying and Mapping Press, 2004. (朱肇光, 孙护, 崔炳光. 摄影测量学[M]. 北京: 测绘出版社, 2004.) |
| [22] | GU Xiaolie, BAO Feng, CHENG Xiaojun. Surveying [M]. 3rd ed. Shanghai: Tongji University Press, 2006. (顾孝烈,鲍峰,程效军. 测量学[M]. 第3版. 上海: 同济大学出版社, 2006.) |