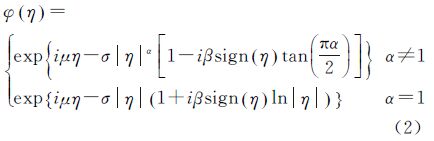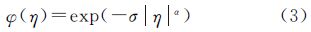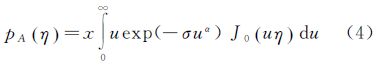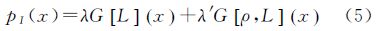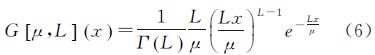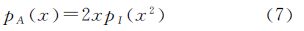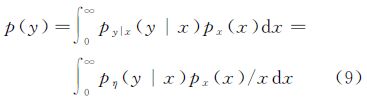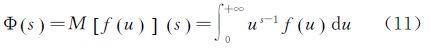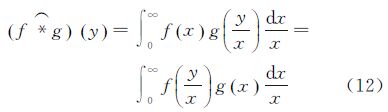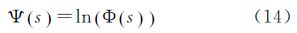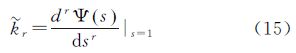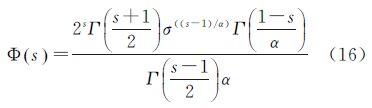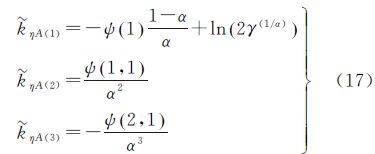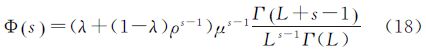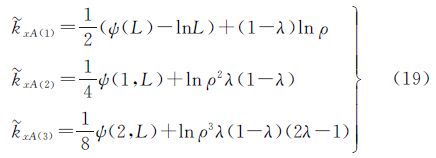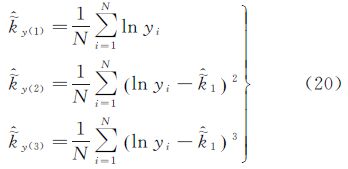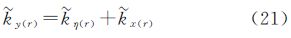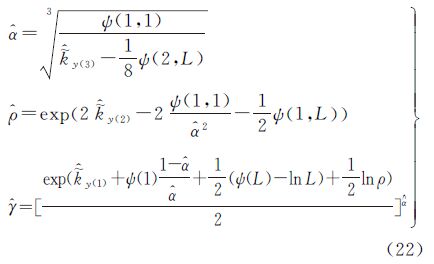1 引 言
SAR图像统计建模是SAR图像研究的重要内容，它旨在通过统计的方法描述SAR图像数据，以解释SAR图像的统计特性[1, 2]。SAR图像统计特性不仅有助于深入了解地物的散射机理，而且合理的SAR图像统计特性可以有效地提高SAR图像相干斑抑制、分割，RCS重构以及目标检测和识别能力[3, 4, 5]。
多年来，多种统计模型相继提出用于刻画SAR图像的统计特征。文献[6]首先提出了广泛使用的相干斑模型。但是因为相干斑模型要求分辨单元的统计特性和均匀区域的统计特性相同，所以只适用于描述均匀杂波背景下SAR图像的统计特性。在相干斑模型的基础上，文献[7]认为SAR图像后向散射系数是地形散射系数受乘性的相干斑噪声的调制而成。因此在这个框架下，SAR图像的统计特性可视为两个独立的随机变量的复合过程。但是服从中心极限定理的乘积模型在假设条件方面受到局限，它只包括了对一般不均匀区域和均匀区域的SAR图像建模。对于异质混合区域或者城市区域等较高不均匀区域，这种分布模型建模有一定的局限性。
针对高分辨率合成孔径雷达SAR图像不再满足中心极限定理的问题，文献[8]在对称α稳态分布的基础上，提出了拖尾Rayleigh幅度分布。拖尾Rayleigh分布具有代数拖尾，因此它们具有异质混合区域或者城市区域SAR图像尖峰和厚尾的统计特性。2006年，文献[9]提出了乘性模型下的拖尾Rayleigh分布模型，并利用新的模型对SAR图像进行相干斑抑制。但是前面提到的模型都忽略了RCS分布模型中的参数[10, 11, 12]，而这些参数在高分辨率合成孔径雷达SAR图像统计建模中有很重要的作用。
在本文中，混合Gamma拖尾Rayleigh分布是由乘积模型推导而得。笔者分别推导出相干斑服从统计模型拖尾Rayleigh分布模型和RCS服从统计模型混合Gamma分布模型。拖尾Rayleigh分布突破了中心极限定理的限制，适合于描述高分辨率SAR相干斑的尖峰厚尾的统计特性[13]；高分辨率合成孔径雷达SAR图像的RCS起伏衰落特性更加的复杂，混合Gamma分布作为不同均值的Gamma分布的线性组合对高分辨率合成孔径雷达SAR图像RCS进行拟合，突破了利用某一种概率分布函数描述RCS的局限性。
SAR图像统计建模的一个重要步骤是参数估计，在本文中，笔者使用的方法是文献[14, 15, 16]提出的由Mellin变换为基础的第二类统计量参数估计方法。相对于传统的矩估计方法，这种方法更简单、有效。
2 SAR图像统计模型设SAR图像的测量值y是两个变量x和η的乘积，这里x为地物RCS分量，η为相干斑噪声分量。根据乘积模型，SAR图像的测量值可表示为
式中，“·”表示乘积，乘积模型同时考虑到相干斑噪声和RCS对SAR图像测量值的影响。通过假设这两个随机变量的统计模型，可以得到不同的SAR图像分布模型。基于乘积模型，已发展了很多著名的SAR图像统计模型，例如K分布、Betaprime分布等，但是对于较高分辨率合成孔径雷达SAR图像的建模，这些模型是有局限性的[9]。在本文中，针对高分辨率合成孔径雷达SAR图像的建模问题，笔者设相干斑噪声随机变量服从拖尾Rayleigh分布，RCS随机变量服从混合Gamma分布。
2.1 相干斑模型对于高分辨SAR图像，一个分辨单元内含有的散射粒子数目足够大的假设不成立。此时，中心极限定理得不到满足，Rayleigh分布模型也不再适合高分辨城区图像统计分布建模。在本文中引入广义中心极限定理下的α稳定模型[17, 18]。相比较中心极限定理下的高斯假设，α稳定假设是一种更有效的模型。
α稳定分布没有解析的概率密度函数表达式，由它的特征函数描述[19]，其表达式如下
式中，0＜α≤2是特征参数，它决定了稳定分布尖峰和厚尾的程度，α越小稳定分布显示出尾部较厚的特征。β≤1是对称参数，当β＜0时，稳定分布向左倾斜；当β>0时，稳定分布向右倾斜；当β=0时，稳定分布关于位置参数对称，此时，稳定分布称为对称稳定分布。σ>0是尺度参数，它类似于高斯分布的方差代表分布的离散程度，μ∈R是位置参数，它表示在横坐标上的偏移，sign(·)是符号函数。α稳定分布由4个参数决定，它是描述尖峰厚尾分布良好的统计模型，通过改变其特征参数能够描述很广范围的非高斯特性。文献[20]使用特殊位置的对称稳定分布，即μ=0,β=0，来描述SAR系统接收信号的实部和虚部，其特征函数如下
由此推导出SAR相干斑概率密度函数积分等式
称为拖尾Rayleigh分布。其中0＜α＜2是特征指数，它描述稳定分布尖峰和厚尾的统计特征；σ>0是尺度参数；J0(·)是第一类零阶Bessel函数。
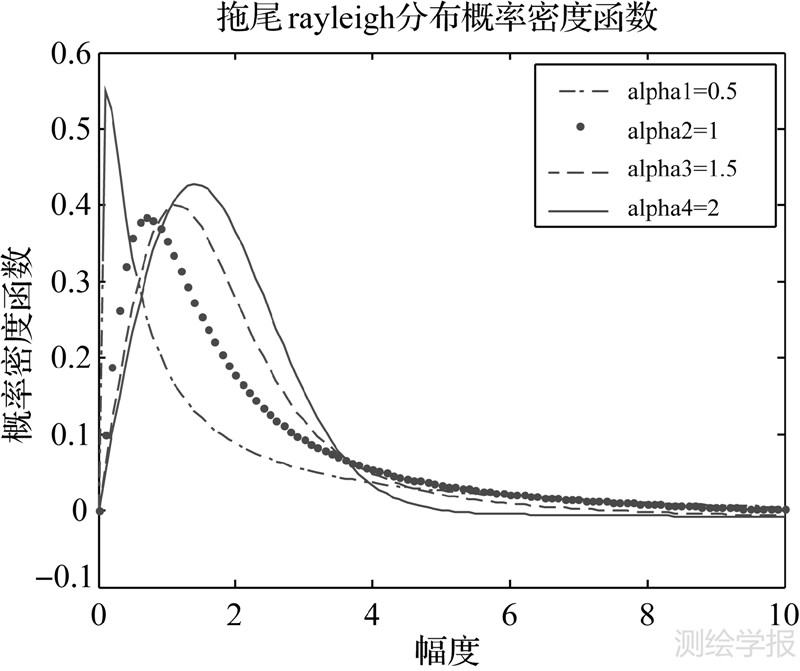
图 1为拖尾Rayleigh分布在α取不同值时的概率密度函数。由图可见，拖尾Rayleigh分布有明显的尖峰和厚尾的统计特征，并且α越小，尖峰和厚尾越明显。
|
| 图 1 拖尾Rayleigh分布在特征指数α取不同值时的概率密度函数 Fig. 1 Heavy-tailed Rayleigh distribution probability density functions for different values of the characteristic exponent α |
SAR图像RCS的起伏特性随着图像分辨率提高变得更加的复杂。笔者提出使用混合Gamma作为高分辨率合成孔径雷达SAR图像RCS的分布模型。相对通常Gamma分布模型具有单一的形式参数，混合Gamma分布拥有多个参数，提供了更多的灵活性，能够模拟更大范围的概率密度，并且具有单峰多模式的特点。
设SAR图像表示为L视强度平均的形式，那么RCS随机变量x服从混合Gamma分布，其概率密度函数表达式为
式中，λ≥0,λ′≥0,且λ+λ′=1，G[L]x表示均值为1，方差为1/L的Gamma分布概率密度函数，G[ρ,L](x)表示均值为ρ，方差为1/L的Gamma分布概率密度函数。在本模型中，两个Gamma分布概率密度函数的L取值相同。其中Gamma分布概率密度函数G[ρ,L](x)的表达式为
通过变量代换关系
可以推导出幅度概率密度函数
混合Gamma拖尾Rayleigh分布是由乘积模型推导而得，设(x,η)是二维随机变量，其中，x表示RCS随机变量，η表示相干斑随机变量，并且x与η是相互独立的。设x与η的概率密度分别为px(x)，pη(η)，则高分辨率合成孔径雷达SAR图像的观测值y=x·η仍然是随机变量，并且由概率论知识可以推导得到其概率密度函数为
将式(4)与式(8)代入式(9)得到基于混合Gamma拖尾Rayleigh分布模型的高分辨率合成孔径雷达SAR图像观测值概率密度函数表达式
式中，α、γ、ρ是混合Gamma拖尾Rayleigh分布的参数，文中使用一种基于Mellin变换的参数估计方法对其进行估计。
3 基于Mellin变换的参数估计为了对SAR图像精确建模，需要对模型参数精确估计。相比较于传统的矩估计方法，文献[14]提出的基于Mellin变换的第二类型统计量参数估计方法可以把相干斑噪声分量视为Mellin卷积，这与SAR图像的乘性噪声特点相吻合，因此是一种更有效的参数估计方法。因而本文选择Mellin变换进行混合Gamma拖尾Rayleigh分布模型的参数估计。
对于定义于R+上的函数f，其Mellin变换定义如下
变换Φ(s)存在当且仅当对任意k>0，积分∫0∞|f(x)|xk－1dx有界，对于SAR图像的概率密度而言，条件是满足的。
函数f和g的Mellin卷积为
由Mellin变换定义函数f的第二类第一特征函数
在第二类第一特征函数的基础上，可以得到第二类第二特征函数和对数累积量分别为
由式(4)、(13)可以得到拖尾Rayleigh分布对应的第二类第一特征函数为
由式(15)、(16)得到拖尾Rayleigh分布推得各阶二类特征矩为
式中，ψ是DiGamma函数，它表示先对Gamma函数取对数然后求导；ψ(r,·)是PolyGamma函数，表示DiGamma函数的第r阶导数。由式(8)、(13)，得到混合Gamma分布的第二类第一特征函数
由式(15)、(18)得到混合Gamma分布各阶对数累积量
设y1、y2、…、yN为N个样本观测值，样本的第1、2、3阶第二类累积量估计值为
由式(12)可知混合Gamma拖尾Rayleigh分布的概率密度函数是混合Gamma函数与拖尾Rayleigh函数的Mellin卷积。因此SAR图像幅度观测值y的对数累积量可以表示为SAR图像RCS值x和SAR图像相干斑η的对数累积量之和
式中，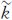
y(r)可以由式(20)根据样本观测值估计得到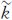；η(r)、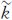x(r)是包含α、γ、ρ的代数表达式。利用式(17)、(19)、(20)和(21)，得到混合Gamma拖尾Rayleigh分布参数α、γ、ρ的估计表达式为
把式(22)称为对数累积量估计器，已知SAR图像样本观测值，它能够获得参数估计值，从而得到SAR图像的统计模型。
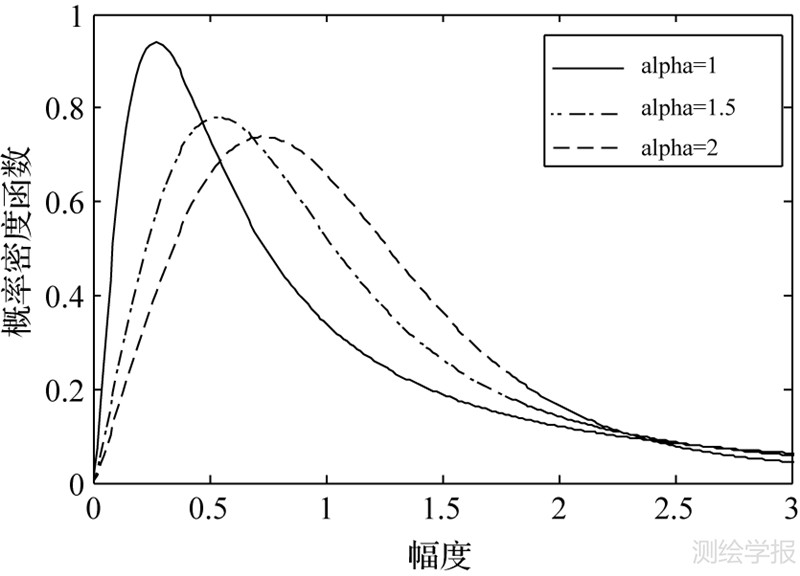
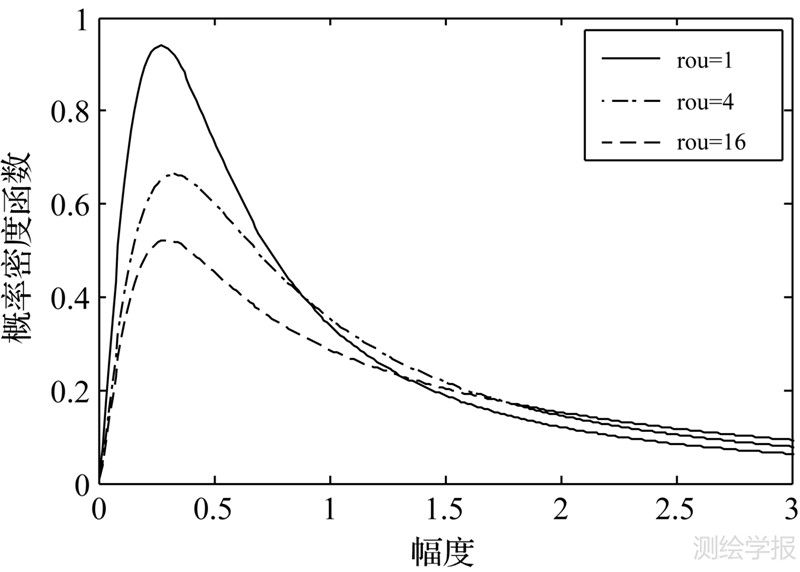
4 混合Gamma拖尾Rayleigh分布的性质本节讨论该分布的性质，以解释该分布能对高分辨SAR图像建模的原因。形状参数α本质上反映了被测区域的尖峰、厚尾的特征，α越小，对应的图像区域越不均匀。图 2给出了固定参数γ=1时，混合Gamma分布的变化曲线，由图 2可知，随着α的减小，尖峰、厚尾特征越明显。但是其他值不变时，峰值的位置随着α的值移动。图 3给出了固定参数α、γ，混合Gamma分布随着ρ增加的变化曲线，从图中看出通过改变ρ可以调解峰值和拖尾的厚度而不改变峰值的位置，相比较已有模型混合Gamma拖尾Rayleigh分布模型，因为增加了一个参数ρ，自由度增加，因此可以更好地适应不同高分辨率SAR图像场景。
|
| 图 2 γ=1，ρ=1时，α取不同值时的混合Gamma分布 Fig. 2 Mixture Gamma distribution for α,when γ、ρ is kept constant 1 |
|
| 图 3 α=1，γ=1，ρ取不同值时的混合Gamma分布 Fig. 3 Mixture gamma distribution for ρ,when α、γ is kept constant 1 |
为验证本文提出的混合Gamma拖尾Rayleigh分布模型的有效性，笔者对实测机载条带SAR图像数据进行拟合。试验数据采用的是机载雷达X波段SAR成像的图像数据，大小为1024像素×1024像素，图像的分辨率为1 m×1 m，图像区域包括草地、农田、公路。本文分别利用Betaprime分布、拖尾Rayleigh分布、K分布和本文提出的混合Gamma拖尾Rayleigh分布分别对SAR图像数据进行拟合，并利用经典的假设检验K-S拟合检验方法进行测试。
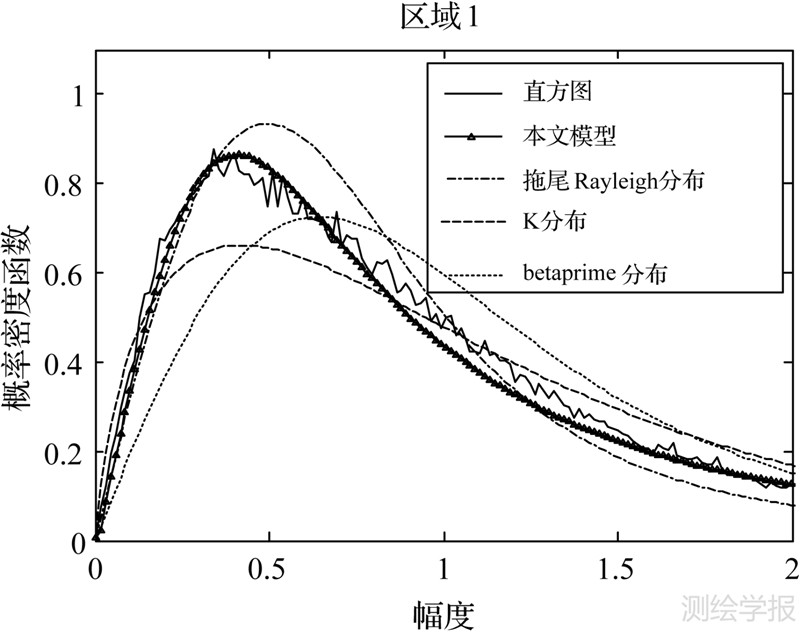
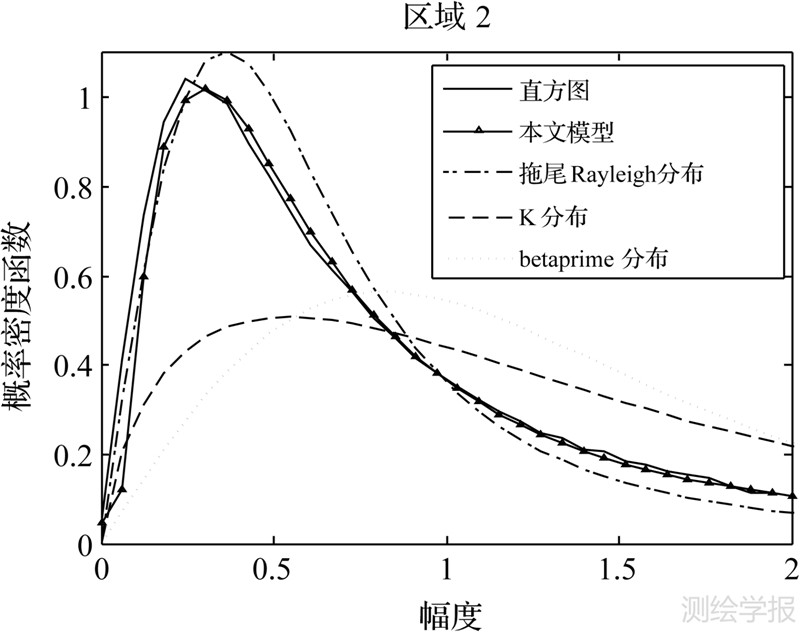
图 5与图 6为分别利用Betaprime分布、拖尾Rayleigh分布、K分布和本文提出的混合Gamma拖尾Rayleigh分布对图 4中右面方框中的区域1中的SAR图像和对图 4中左边面方框中的区域2中的SAR图像建模的拟合效果图。表 1与表 2分别给出了不同分布的参数估计结果及K-S概率。K-S概率用来定量描述某一分布对图像统计分布的接近程度，K-S概率越大，说明该分布越接近图像的统计分布。结果表明，基于中心极限定理的Betaprime分布和K分布在一定程度上描述了图像的拖尾特征，但是它们不能反映SAR图像的尖峰特征。拖尾Rayleigh分布虽然能够大致描述SAR图像的尖峰拖尾特征，但是由于此模型假设SAR图像RCS为常数，所以它还是不能准确地描述高分辨率SAR图像。由拟合效果图和数据分析都可得到本文提出的混合Gamma拖尾Rayleigh分布能够比较准确地描述高分辨SAR图像，这是因为混合Gamma拖尾Rayleigh分布不仅具有拖尾Rayleigh分布尖峰拖尾的特征，而且混合Gamma分布具有很好的灵活性，能够模拟更大范围的概率密度，模型的适应性更强。
|
| 图 4 X波段SAR图像 分辨率1 m Fig. 4 X-band SAR image,the resolution is 1 m |
|
| 图 5 对实测SAR图像中的区域1的建模结果 Fig. 5 Modeling results of the area 1 in the real SAR image |
|
| 图 6 对实测SAR图像中的区域2的建模结果 Fig. 6 Modeling results of the area 2 in the real SAR image |
| 概率分布 | 参数值 | 概率 |
| 本文模型 | α=1.524 5,γ=0.268 5,ρ=3.385 4 | 0.999 5 |
| 拖尾Rayleigh分布 | α=1.493 8,γ=0.284 3 | 0.836 5 |
| K分布 | α=1,γ=1.986 6 | 0.247 2 |
| Beta-prime分布 | α=1.687 5,γ=2.141 7 | 0.032 1 |
| 概率分布 | 参数值 | 概率 |
| 本文模型 | α=1.328 4,γ=0.246 6,ρ=4.375 8 | 0.997 7 |
| 拖尾Rayleigh分布 | α=1.307 9,γ=0.259 2 | 0.876 5 |
| K分布 | α=1,γ=3.365 5 | 1.283 5e-12 |
| Beta-prime分布 | α=2.003 4,γ=3.376 9 | 7.695 4e-18 |
利用拖尾Rayleigh分布尖峰拖尾和混合Gamma分布灵活性强的特点，本文提出了一种基于乘积模型的混合Gamma拖尾Rayleigh分布模型。针对已有模型不能很好地对高分辨SAR图像进行拟合的问题，该模型利用基于广义中心极限定理的拖尾Rayleigh分布作为相干斑模型，反映了高分辨率SAR图像相干斑尖峰和拖尾的特点；利用混合Gamma分布作为RCS模型，提高了RCS模型的灵活性，能很好地反映高分辨SAR图像中的RCS的细微变化。并以Mellin变换为基础，利用第二类统计量、第二类特征函数、第二类对数矩和第二类累积量，可以高效估计出混合Gamma拖尾Rayleigh分布的未知参数。利用实际的高分辨合成孔径雷达SAR图像进行的试验结果证明了基于乘积模型的混合Gamma拖尾Rayleigh分布对高分辨SAR图像建模更有效。混合Gamma拖尾Rayleigh分布模型能够对合成孔径雷达SAR图像中地物的散射机理有更深入的理解，进而指导研究有效的高分辨率合成孔径雷达SAR图像相干斑抑制、纹理提取、图像分割与目标识别算法。
| [1] | HUANG Shiqi, LIU Daizhi. Research on Method and Application of Speckle Noise Reduction of SAR Image[J].Acta Geodaetica et Cartographica Sinica, 2006, 35(3): 245-250.(黄世奇,刘代志. SAR 图像斑点噪声抑制方法与应用研究[J]. 测绘学报, 2006, 35(3): 245-250.) |
| [2] | SOUMEKH M. Synthetic Aperture Radar Signal Processing[M]. New York: Wiley, 1999. |
| [3] | WU Yan, JIAO Jingmei, YANG Xiaoli, et al. Segmentation Algorithm for SAR Images Based on Fusion of HMT in the Contourlet Domain and D -S Theory of Evidence[J]. Acta Geodaetica et Cartographica Sinica,2011, 40(2): 148-155.(吴艳,焦惊眉,杨晓丽,等. 基于 Contourlet 域 HMT 和 DS 证据融合的 SAR 图像分割[J]. 测绘学报, 2011, 40(2): 148-155.) |
| [4] | ZHANG Zhongshan, YU Jie, YAN Qin, et al. Research on Polarimetric SAR Image Speckle Reduction Using Kernel Independent Component Analysis[J]. Acta Geodaetica et Cartographica Sinica,2011, 40(3): 289-295.(张中山,余洁,燕琴,等. 基于核独立成分分析的极化 SAR 图像相干斑抑制[J]. 测绘学报,2011, 40(3): 289-295.) |
| [5] | WAN Honglin, JIAO Licheng, WANG Guiting, et al. A Region-of-interest Level Method for Change Detection in SAR Imagery[J].Acta Geodaetica et Cartographica Sinica,2012, 41(2): 239-245.(万红林,焦李成,王桂婷,等. 在感兴趣的区域层面上进行 SAR 图像变化检测的方法研究[J]. 测绘学报, 2012, 41(2): 239-245.) |
| [6] | ARSENAULT H H, APRIL G. Properties of Speckle Integrated with a Finite Aperture and Logarithmically Transformed[J]. Journal of the Optical Society of America, 1976, 66(11): 1160-1163. |
| [7] | WARD K D. Compound Representation of High Resolution Sea Clutter[J]. Electronics Letters, 1981, 17(16): 561-563. |
| [8] | KURUOGLU E E, ZERUBIA J. Modeling SAR Images with a Generalization of the Rayleigh Distribution[J]. IEEE Transactions on Image Processing, 2004, 13(4): 527-533. |
| [9] | ACHIM A, KURUOGLU E E, ZERUBIA J. SAR Image Filtering Based on the Heavy-Tailed Rayleigh Model[J]. IEEE Transactions on Image Processing, 2006, 15(9): 2686-2693. |
| [10] | JAO J. Amplitude Distribution of Composite Terrain Radar Clutter and the K-distribution[J]. IEEE Transactions on Antennas and Propagation, 1984, 32(10): 1049-1062. |
| [11] | LI H C, HONG W, WU Y R, et al. An Efficient and Flexible Statistical Model Based on Generalized Gamma Distribution for Amplitude SAR Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(6): 2711-2722. |
| [12] | HUANG Shiqi, LIU Daizhi, HU Mingxing, et al. Multi-temporal SAR Image Change Detection Technique Based on Wavelet Transform[J]. Acta Geodaetica et Cartographica Sinica,2010, 39(2): 180-186.(黄世奇,刘代志,胡明星,等. 基于小波变换的多时相 SAR 图像变化检测技术[J]. 测绘学报, 2010, 39(2): 180-186.) |
| [13] | ACHIM A, TSAKALIDES P, BEZERIANOS A. SAR Image Denoising via Bayesian Wavelet Shrinkage Based on Heavy-Tailed Modeling[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(8): 1773-1784. |
| [14] | TISON C, NICOLAS J M, TUPIN F, et al. A New Statistical Model for Markovian Classification of Urban Areas in High-Resolution SAR Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(10): 2046-2057. |
| [15] | SHI Gongtao, ZHAO Lingjun, GUI Lin, et al.A Novel Parameter Estimation Method for the K Distribution Based on the Mellin Transform[J]. Acta Electronica Sinica,2010, 38(009): 2083-2089.(时公涛,赵凌君,桂琳,等. 基于 Mellin 变换的 K 分布参数估计新方法[J]. 电子学报, 2010, 38(009): 2083-2089.) |
| [16] | SUN Zengguo,HAN Chongzhao. Modeling High-Resolution Synthetic Aperture Radar Images with Heavy-tailed Distributions[J].Acta Physica Sinica,2010,59(2)998-1008.(孙增国,韩崇昭. 基于拖尾分布的高分辨率合成孔径雷达图像建模[J]. 物理学报, 2010, 59(2)998-1008.) |
| [17] | OLIVER C, QUEGAN S. Understanding Synthetic Aperture Radar Images[M]. Herndon: SciTech Publishing, 2004. |
| [18] | KUANG Gangyao, GAO Gui, JIANG Yongmei, et al. Synthetic Aperture Radar Target Detection Theory Algorithms and Applications[M]. Chang National University of Defense Technology Press,2007.(匡纲要, 高贵,蒋咏梅,等. 合成孔径雷达目标检测理论, 算法及应用[M]. 长沙:国防科技大学出版社, 2007.) |
| [19] | NICOLAS J M. Introduction to Second Kind Statistics: Application of Log-Moments and Log-cumulants to SAR Image Law Analysis[J]. Traitement du Signal, 2002, 19(3): 139-168. |
| [20] | DELIGNON Y, PIECZYNSKI W. Modeling Non-Rayleigh Speckle Distribution in SAR Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(6): 1430-1435. |