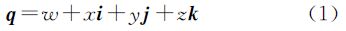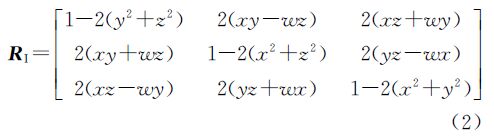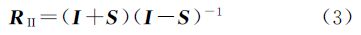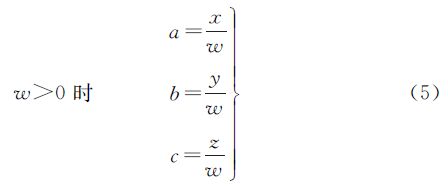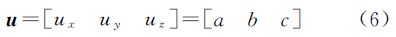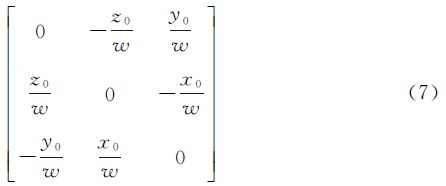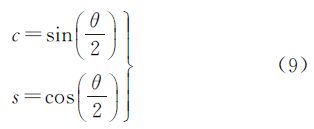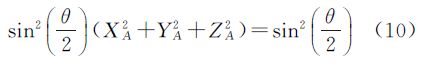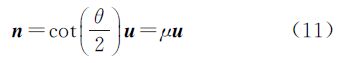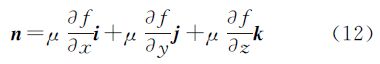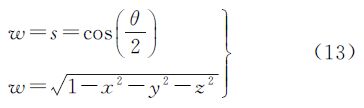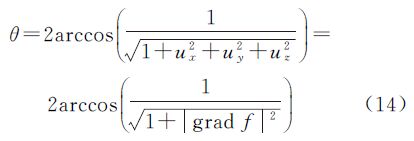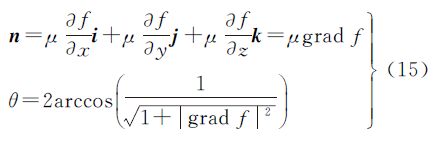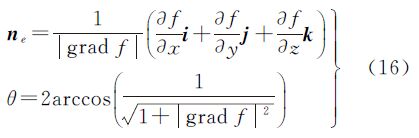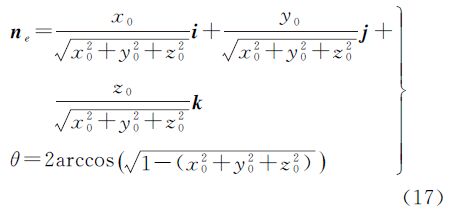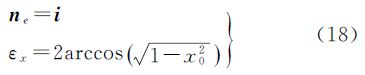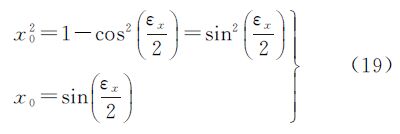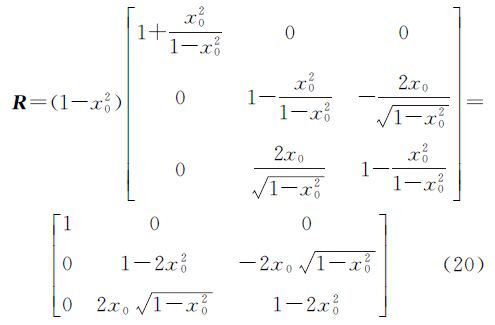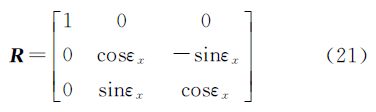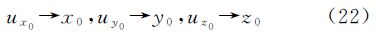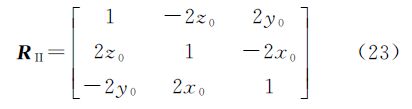2. 中国科学院大学,北京 100049;
3. 信息工程大学 地理空间信息学院,河南 郑州 450052
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Institute of Geospatial Information, Information Engineering University, Zhengzhou 450052, China
在测量工作中,空间直角坐标基准转换工作的地位极其重要,如在大地测量中,经常遇到WGS-84坐标系到1954北京坐标系或是1980西安坐标系的转换,以及国家坐标系到地方坐标系的转换等[1, 2, 3, 4]。在以往的工作中,一般采用小角度模型进行空间坐标转换,如众所周知的布尔沙-沃尔夫(Bursa-Wolf)转换模型、莫洛金斯基转换模型和范士转换模型等[5, 6, 7, 8, 9]。文献[6]将众多的坐标转换数字模型统一为线性回归模型,提出了模型的检验方法,并将其统一于线性约束的回归模型。在处理大角度转换问题时,可对作业方法进行改进,使大旋转角变成小旋转角;或先将大旋转角近似地改正后转换成小旋转角,再采用小旋转角的空间直角转换模型,上述方法的目的都是为了简化计算过程,避免复杂的数学模型,因为在大旋转角的空间坐标转换中,需要处理极为复杂的非线性问题且过程非常复杂,计算误差也较大,不能保证其精度及合理性[1]。文献[8]讨论了三维坐标转换的线性模型的应用范围,提出了三维坐标转换的非线性模型,解决了模型对旋转角大小的限制。文献[9]针对我国平面控制网与高程控制网分开布设的特点,借助过渡坐标系,改进了计算坐标转换参数的常用模型。
在实际工作中,很多领域不可避免地会遇到大旋转角的空间坐标转换问题,而且在许多情况下不能对模型进行线性处理[1]。对此,许多学者进行了深入研究,提出了一些能够适用于大旋转角的空间坐标转换模型[10, 11, 12, 13, 14],如利用罗德里格矩阵代替方向余弦矩阵的方法和利用四元数构造旋转矩阵等。文献[10]利用反对称矩阵和罗德里格矩阵的性质,把传统的3个旋转角参数用反对称矩阵的3个独立元素代替,解决了任意角度的坐标系变换问题。文献[14]提出一种基于四元数构造旋转矩阵来解算三维空间相似变换模型的方法,结果表明该方法可适用于大旋转角度的坐标变换。
以上关于空间坐标系变换的文章研究的都是固定的、静态的空间坐标系之间的变换问题(如1954北京坐标系到1980西安坐标系之间的转换等)。对于大角度的空间坐标系变换虽有理论研究,但主要还是固定的、静态(旋转角不随时间发生变化)的空间坐标系之间的变换问题。如何在理论上将空间坐标系变换由小角度推广到任意角度、由静态推广到动态,即研究空间坐标系随时间发生连续变换、任意角度连续变换的情况(能够为确定运动载体的姿态提供一种新思路、新方法),需要研究和深入探讨空间坐标系变换的本质问题。
基于单位四元数构造的旋转矩阵与罗德里格矩阵两者的内在一致性,本文从更深层次上探讨空间坐标系变换的本质,提出用函数梯度描述空间坐标系变换的方法。理论研究表明,空间坐标系变换对应函数梯度场,即空间坐标系变换的本质是“场”,可以用“场”的概念统一以任意角度发生旋转变换的空间坐标系变换特例。从而在理论上为进一步研究任意角度的空间坐标系变换,尤其是空间坐标系随时间发生连续变换的情况奠定理论基础。
2 基于单位四元数的旋转矩阵与罗德里格矩阵文献[15—18]提出四元数的概念,认为四元数是一个有着4个元素的列向量,用矢量表示见式(1)
式中,w为实部;i、j、k为虚部。单位四元数需要满足下式
对于罗德里格矩阵,设反对称矩阵为
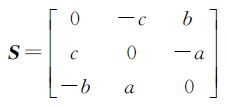
将反对称矩阵S代入式(3),经过有关矩阵运算可得
式(4)即为罗德里格矩阵的完整形式。基于单位四元数构造的旋转矩阵式(2),经常应用在摄影测量与遥感领域,用四元数描述三维旋转以及运动载体的姿态具有优越性[14, 15, 16, 17, 18]。文献[16]指出采用单位四元数描述相机姿态,可较好地克服欧拉角在空间方位的描述和插值中的局限性;文献[17]介绍了四元数的概念及运算性质,提出利用单位四元数表示旋转的方法,给出了基于单位四元数的空间后方交会解算方法及其计算公式,并证明了该方法对角元素不加任何限制,适用于大倾角摄影的航片;文献[14]研究表明,基于单位四元数的旋转矩阵可以适用于小角度、大角度以及任意角度的空间坐标系变换。罗德里格矩阵经常应用于大地测量领域,特别是在研究大角度的空间坐标系的变换时,在计算的简易程度方面相对于空间欧拉角具有明显的优越性,且适用于任意角度的空间坐标系变换[1, 10]。
以上分析说明,基于单位四元数构造的旋转矩阵RI和罗德里格矩阵RII均能够表示空间任意角度的坐标系变换。那么,RI和RII在数学上存在统一性或完全等价性条件吗?如果此完全等价性条件存在,则空间坐标系变换就对应此完全等价性条件。
3 基于单位四元数的旋转矩阵和罗德里格矩阵的完全等价条件
由单位四元数的归一化条件
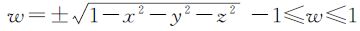 ,
,
若令w>0
则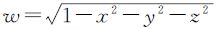
令罗德里格矩阵中的3个独立元素a、b、c分别为
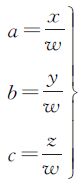
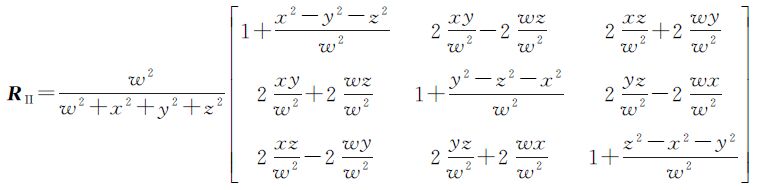
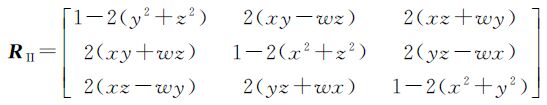
上式右边便是单位四元数构造的旋转矩阵RI。
综上分析,如果罗德里格矩阵要转化为单位四元数构造的旋转矩阵,需要满足如下条件(仅考虑w>0时的情况,对于w<0,与此类似,不再赘述)
然而,当w→0时,a、b、c同时趋近于无穷大。因此在罗德里格矩阵向基于单位四元数构造的旋转矩阵转化的过程中,会出现“奇点”现象。如果假设空间向量
则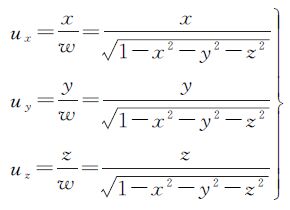
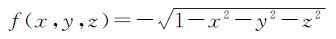
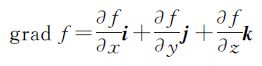
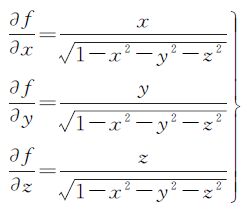
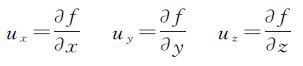
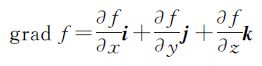
u为函数f(x,y,z)的梯度。由以上证明过程可知,罗德里格矩阵与基于单位四元数构造的旋转矩阵完全等价,针对的不是函数f(x,y,z)在某点处的具体的梯度向量,而是它的所有点的梯度向量,是所有点处的梯度向量所组成的区域或者空间。因此,罗德里格矩阵与基于单位四元数的旋转矩阵完全等价所要求的条件是,函数f(x,y,z)在其定义域内的所有点处的梯度向量所组成的向量空间。
在高等数学中,对于“场”的概念有明确的定义,即如果对于空间区域G内的任意一点M,都有一个确定的数量f(M),则称在这空间区域G内确定了一个数量场。一个数量场可以用一个数量函数f(M)来确定。如果与点M相对应的是一个向量F(M),则称在这空间区域G内确定了一个向量场。一个向量场可以用一个向量值函数F(M)来确定,而
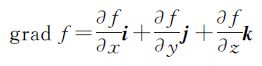
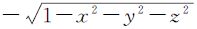 的梯度场上,由空间单位四元数构造的旋转矩阵与罗德里格矩阵完全等价。这也在数学上证明了,空间存在向量u=(ux0,uy0,uz0)=grad f(x0,y0,z0),该向量构成反对称矩阵S
的梯度场上,由空间单位四元数构造的旋转矩阵与罗德里格矩阵完全等价。这也在数学上证明了,空间存在向量u=(ux0,uy0,uz0)=grad f(x0,y0,z0),该向量构成反对称矩阵S
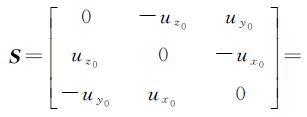
综上可知,函数f(x,y,z)=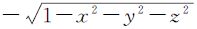 (定义域:x2+y2+z2≤1单位球体)在不同点处的梯度向量将对应不同的罗德里格矩阵,即表示不同的坐标系旋转矩阵,(广义上)表示不同的空间坐标系变换情况。由于式(3)表示的是任意旋转矩阵,因此,只有在函数f(x,y,z)=
(定义域:x2+y2+z2≤1单位球体)在不同点处的梯度向量将对应不同的罗德里格矩阵,即表示不同的坐标系旋转矩阵,(广义上)表示不同的空间坐标系变换情况。由于式(3)表示的是任意旋转矩阵,因此,只有在函数f(x,y,z)=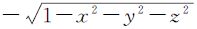 某点处的梯度方向上,罗德里格矩阵才表示该点处的旋转矩阵。而在该点处的其他方向上,旋转矩阵就不能由该点处的罗德里格矩阵表示(即此时的罗德里格矩阵不表示该点处的旋转矩阵)。
某点处的梯度方向上,罗德里格矩阵才表示该点处的旋转矩阵。而在该点处的其他方向上,旋转矩阵就不能由该点处的罗德里格矩阵表示(即此时的罗德里格矩阵不表示该点处的旋转矩阵)。
按照上述观点可得一个奇特的结论,三维空间两个确定的坐标系之间的变换(如1954北京坐标系到1980西安坐标系的转换)对应一条确定的(三维)梯度向量,即可以用一条梯度向量来描述。如果上述观点成立,则描述两个确定的空间坐标系之间的旋转变换仅用一条(三维)向量就足够了。下面将证明上述结论。
4 空间坐标系变换与函数梯度场4.1 空间坐标系变换的梯度场描述
用向量n和旋转角θ来描述空间两坐标系的旋转或变换。考虑到这样一个基本事实:空间任何一个旋转或变换都可看成绕着某一个旋转轴(三维空间向量)旋转某一个角度而成[14]。这也是空间坐标系变换最直接的描述方法。假设空间某两坐标系间的变换是通过一条旋转轴向量n=[XA YA ZA]和一个旋转角θ(-π≤θ≤π)来实现的,并且空间单位四元数向量为q=[x y z w],则其4个元素可定义为[14]
其中 考虑单位四元数的归一化条件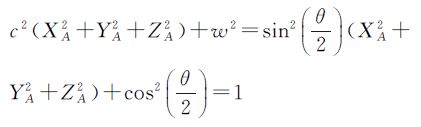
现在考虑空间坐标系OXYZ,O为坐标系原点;X、Y、Z为3个坐标轴,假设其绕n=[XA YA ZA]旋转θ角(n非零)。由于单位四元数归一化条件的约束,式(10)实际表达了如下两方面含义:
(1) 如果旋转角θ=0,说明OXYZ没有发生旋转,则由式(10)可得XA2+YA2+ZA2=C (C为任意大于零的实数),因此向量n=[XA YA ZA]是任意向量,其对应除原点(0,0,0)之外的整个三维矢量空间。
(2) 如果旋转角θ≠0,说明OXYZ发生了旋转,则由式(7)可得XA2+YA2+ZA2=1,因此,向量n=[XA YA ZA]是单位向量,其几何意义是单位球面。因此,单位四元数的归一化条件将空间任意角度的坐标系变换情况压缩到了单位球面上。
以上两种情况表明,由于单位四元数的归一化条件使得用一条三维向量来描述坐标系变换变得困难起来。因此在三维空间内,单独用单位四元数向量无法描述空间坐标系变换,必须将单位四元数与罗德里格矩阵中的3个独立元素结合起来考虑问题。
考虑单位四元数的4个元素的定义式(8)、式(9),可得
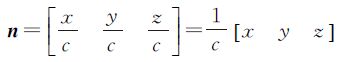
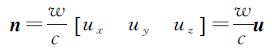
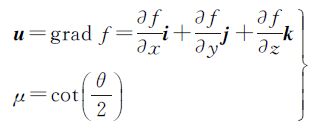
综上,可得含有系数的公式为
式中,系数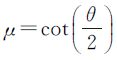 。
。
在式(15)中,由于n表示的是空间坐标系的旋转轴指向向量,与自身系数无关,可将式(15)中的μ去掉,并令空间坐标系的旋转轴指向向量为单位矢量ne,可进一步得到由函数梯度表示的空间坐标系变换的数学公式
式中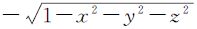 0≤x2+y2+z2≤1
0≤x2+y2+z2≤1
式(16)说明空间任意坐标系转换都可看成是:绕着函数f(x,y,z)=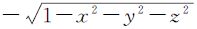 在某点处的单位梯度向量ne作θ角旋转得到,而θ角的大小由梯度模的大小决定,因此空间坐标系变换完全由函数梯度决定。
在某点处的单位梯度向量ne作θ角旋转得到,而θ角的大小由梯度模的大小决定,因此空间坐标系变换完全由函数梯度决定。
根据以上论证可得出结论:空间确定的两个坐标系之间的变换对应一确定的函数梯度向量,可以用一条梯度向量进行描述,要确定两个空间坐标系之间的变换问题,就是确定函数f(x,y,z)=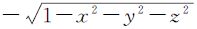 在某点处的梯度向量,即确定梯度向量u=[ux uy uz]。
在某点处的梯度向量,即确定梯度向量u=[ux uy uz]。
对于一般情况或者广义的空间坐标系变换,即为空间坐标系变换对应函数梯度场。因此根据式(16)以及在数学上对于“场”的定义可以得出结论,空间坐标系变换在本质上是一种“场”。
4.2 布尔莎(Bursa)模型的梯度场描述
由上面论述可知,空间坐标系变换对应函数梯度场。布尔沙模型作为一种空间坐标系的转换模型[8, 9, 10, 11, 19, 20],必然能从函数f(x,y,z)=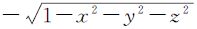 的梯度场导出。设点(x0,y0,z0)是该函数定义域内的任一点,则该点处梯度向量u0=[ux0 uy0 uz0]为
的梯度场导出。设点(x0,y0,z0)是该函数定义域内的任一点,则该点处梯度向量u0=[ux0 uy0 uz0]为
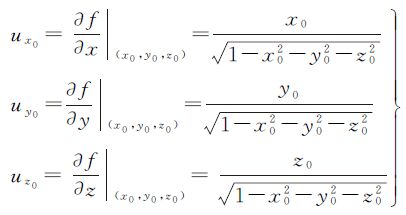
第1类情况:假设点p坐标为(x0,0,0)并且(x0>0),则p点梯度向量为:(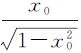 ,0,0),将p点坐标代入式(17),可得
,0,0),将p点坐标代入式(17),可得
由式(18),可得 即
罗德里格矩阵中的3个独立元素实际为函数f(x,y,z)的梯度向量,因此将梯度向量(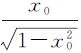 ,0,0)代入罗德里格矩阵,经化简可得到
,0,0)代入罗德里格矩阵,经化简可得到
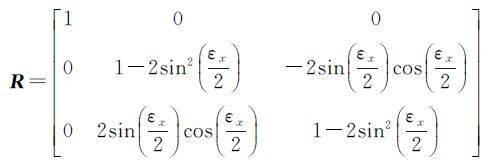
第2类情况:假设点p(x0,y0,z0)不在坐标轴上的任意一点,当x0 2+y0 2+z0 2→0时,即所取点位趋近于原点O(0,0,0)时
将式(22)代入罗德里格矩阵,可得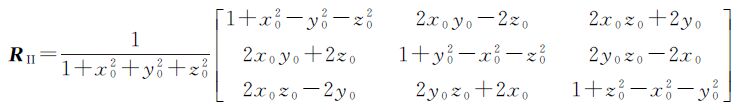
当x0、y0、z0分别取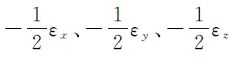 时,则式(23)可以化为
时,则式(23)可以化为

因此,综合以上两类情况的证明过程可进一步验证式(16)的正确性以及在理论上可对布尔莎模型作出梯度场的描述。
按照空间坐标系变换对应函数梯度场的观点,布尔沙模型等空间小角度的坐标系变换对应的是函数f(x,y,z)=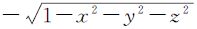 点(
点(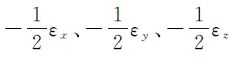 )处的梯度向量所组成的区域,即梯度场(其中,εx、εy、εz都为绝对值很小的数)。因此,对于像布尔莎模型要解决的空间小角度的坐标系转换对应的是函数f(x,y,z)在其定义域内离原点较近处点的梯度所形成的势场;对于较大角度的空间坐标系变换对应的是函数f(x,y,z)在其定义域内离原点较远处点的梯度所形成的势场。
)处的梯度向量所组成的区域,即梯度场(其中,εx、εy、εz都为绝对值很小的数)。因此,对于像布尔莎模型要解决的空间小角度的坐标系转换对应的是函数f(x,y,z)在其定义域内离原点较近处点的梯度所形成的势场;对于较大角度的空间坐标系变换对应的是函数f(x,y,z)在其定义域内离原点较远处点的梯度所形成的势场。
在大地测量学中,εx、εy、εz称为空间欧勒角,用它描述空间坐标系变换比较形象直观。对于大角度的变换情况,会涉及非线性问题线性化的问题,往往会造成较大的模型误差或使模型解算过程烦琐等缺点[6, 7]。由于在三维空间中,点位和向量是一一对应的,式(16)已经表明,空间坐标系变换与向量一一对应,因此,空间坐标系变换亦与三维空间中的点位产生一一对应的关系。按照这样的思路,可将以任意角度发生旋转变换的空间坐标系变换的特例转化成为三维空间之中的点位,按照点位去研究空间坐标系变换问题,可使要研究的问题变得更加方便和直观,笔者将在后续工作中作进一步研究。
空间小角度的坐标系变换对应的是函数f(x,y,z)在其定义域内离原点较近处点的梯度所形成的势场;较大角度的空间坐标系变换对应的是函数f(x,y,z)在其定义域内离原点较远处点的梯度所形成的势场;将空间坐标系变换视为“场”的观点很容易理解:坐标系变换可看成矢量,即它是一个既有大小又有方向的量,方向就是旋转轴指向,大小就是旋转角大小的弧度值。通过空间坐标系变换的数学公式——式(16)可知,空间坐标系变换的方向为梯度方向,大小由该梯度的模决定。其实,上述观点已经蕴含了一种空间坐标系变换的“统一”思想。值得说明的是,本文着力探讨空间坐标系变换的本质问题,由于空间坐标系变换中的平移和伸缩不能改变空间坐标系变化的本质,即“场”的特性,考虑到在空间坐标系变换中,平移因子和尺度因子相对于旋转矩阵的确定要容易得多,因此本文不涉及平移和伸缩问题。
| [1] | PAN Guorong, ZHAO Pengfei. 3D Datum Transformation Model Based on Space Vector[J]. Journal of Geodesy and Geodynamics, 2009, 29(6):79-82.(潘国荣, 赵鹏飞. 基于空间向量的三维基准转换模型[J]. 大地测量与地球动力学,2009, 29(6): 79-82.) |
| [2] | CHENG Yingyan, CHENG Pengfei, BEI Jinzhong, et al. A Study of Coordinate Transformation Methods from WGS-84 to 1980 Xi’an Coordinate System in Large Space Domain[J]. Bulletin of Surveying and Mapping, 2007(12):5-8.(成英燕,程鹏飞,秘金钟,等. 大尺度空间域下1980西安坐标系与WGS-84坐标系转换方法研究[J]. 测绘通报,2007(12):5-8.) |
| [3] | WANG Jiexian, WANG Jun, LU Caiping. Problem of Coordinate Transformation between WGS-84 and Beijing54[J]. Journal of Geodesy and Geodynamics, 2003,23(3):70-73.(王解先,王军,陆彩萍. WGS-84与北京54坐标的转换问题[J]. 大地测量与地球动力学,2003,23(3):70-73.) |
| [4] | PAN Guorong, ZHOU Yueyin. Comparison between Two Ways of Calculation of Coordinate Transfer[J]. Journal of Geodesy and Geodynamics, 2011,31(3):58-62. (潘国荣,周跃寅. 两种坐标系转换计算方法的比较[J]. 大地测量与地球动力学,2011,31(3):58-62.) |
| [5] | SHEN Yunzhong, HU Leiming, LI Bofeng. Ill-posed Problem in Determination of Coordinate Transformation Parameters with Small Area’s Data Based on Bursa Model[J]. Acta Geodaetica et Cartographica Sinica, 2006,35(2):95-98.(沈云中,胡雷鸣,李博峰. Bursa 模型用于局部坐标变换的病态问题及其解法[J]. 测绘学报,2006,35(2):95-98.) |
| [6] | LV Zhiping, ZHU Huatong. The Testing and the Unified Expression of Coordinate Transformation Models[J]. Acta Geodaetica et Cartographica Sinica, 1993,22(3):161-168.(吕志平,朱华统. 坐标转换模型的检验及统一表达[J]. 测绘学报,1993,22(3):161-168.) |
| [7] | YUAN Qing, LOU Lizhi, CHEN Weixian. The Application of the Weighted Total Least-squares to Tree Dimensional-Datum Transformation[J]. Acta Geodaetica et Cartographica Sinica, 2011,40(sup): 115-119.(袁庆,楼立志,陈玮娴.加权总体最小二乘在三维基准转换中的应用[J]. 测绘学报,2011,40(S0):115-119.) |
| [8] | ZENG Wenxian, TAO Benzao. Non-linear Adjustment Model of Three-dimensional Coordinate Transformation[J]. Geomatics and Information Science of Wuhan University,2003,28(5):566-568.(曾文宪,陶本藻. 三维坐标转换的非线性模型[J]. 武汉大学学报:信息科学版,2003,28(5):566-568.) |
| [9] | SHEN Yunzhong, WEI Gang. Improvement of Three Dimensional Coordinate Transformation Model by Use of Interim Coordinate System[J]. Acta Geodaetica et Cartographica Sinica, 1998,27(2):161-165.(沈云中,卫刚. 利用过渡坐标系改进3维坐标转换模型[J]. 测绘学报,1998,27(2):161-165.) |
| [10] | YAO Jili, HAN Baomin, YANG Yuanxi. Application of Lodrigues Matrix in 3D Coordinate Transformation[J]. Geomatics and Information Science of Wuhan University, 2006, 31(12): 1094-1096.(姚吉利, 韩保民, 杨元喜. 罗德里格矩阵在三维坐标系转换严密解算中的应用[J]. 武汉大学学报:信息科学版,2006,31(12): 1094-1096.) |
| [11] | YANG Shiping, FAN Dongming, LONG Yuchun. Three-dimensional Coordination Transformation Adapted to Arbitrary Rotation Angle Based on Total Least Squares Method[J]. Journal of Geodesy and Geodynamics, 2013,33(2):114-119.(杨仕平,范东明,龙玉春.基于整体最小二乘法的任意旋转角度三维坐标转换[J]. 大地测量与地球动力学,2013,33(2):114-119.) |
| [12] | CHEN Yi, SHEN Yunzhong, LIU Dajie. A Simplified Model of Three Dimensional-datum Transformation Adapted to Big Rotation Angle[J]. Geomatics and Information Science of Wuhan University, 2004,29(12):1101-1105.(陈义,沈云中,刘大杰.适用于大旋转角的三维基准转换的一种简便模型[J].武汉大学学报:信息科学版,2004,29(12):1101-1105.) |
| [13] | YOU Wei, FAN Dongming,HUANG Ruijin. A Method of 3D Rectangular Coordinate Transformation Adapted to Any Rotation Angle[J]. Science of Surveying and Mapping, 2009,34(5):154-155.(游为,范东明,黄瑞金. 适用于任意旋转角的三维直角坐标转换方法[J].测绘科学,2009,34(5):154-155.) |
| [14] | ZHAO Shuangming, GUO Qiuyan, LUO Yan, et al. Quaternion-based 3D Similarity Transformation Algorithm[J]. Geomatics and Information Science of Wuhan University, 2009, 34(10):1214-1217.(赵双明,郭秋燕,罗研,等. 基于四元数的三维空间相似变换解算[J].武汉大学学报:信息科学版,2009, 34(10): 1214-1217.) |
| [15] | JIANG Gangwu, JIANG Ting, WANG Yong, et al. Space Resection Independent of Initial Value Based on Unit Quaternions[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 169-175. (江刚武,姜挺,王勇, 等. 基于单位四元数的无初值依赖空间后方交会[J]. 测绘学报,2007,36(2):169-175.) |
| [16] | LIU Jun, WANG Donghong, ZHANG Yongsheng. et al. Bundle Adjustment of Airborne Three Line Array Imagery Based on Unit Quaternion[J]. Acta Geodaetica et Cartographica Sinica, 2008,37(4):451-457.(刘军,王冬红,张永生,等.基于单位四元数的机载三线阵影像光束法平差[J].测绘学报,2008,37(4):451-457.) |
| [17] | GUAN Yunlan, CHENG Xiaojun, ZHOU Shijian, et al. A Solution to Space Research Based on Unit Quaternion[J]. Acta Geodaetica et Cartographica Sinica, 2008,37(1):30-35.(官云兰,程效军,周世健,等. 基于单位四元数的空间后方交会解算[J].测绘学报,2008,37(1):30-35.) |
| [18] | GONG Hui, JIANG Ting, JIANG Gangwu, et al. Solution of Exterior Orientation Parameters for High-resolution Imagery Based on Quaternion Differential Equation[J]. Acta Geodaetica et Cartographica Sinica, 2012,41(3):409-416.(龚辉,姜挺,江刚武,等. 四元数微分方程的高分辨率卫星遥感影像外方位元素求解[J]. 测绘学报,2012,41(3):409-416.) |
| [19] | ZHANG Senlin. Rodrigues Marix in the Use of Rigorous Solution of the Collinearity Equation[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1987,12(1):81-91.(张森林.罗德里格矩阵在共线方程严密解法中的应用[J].武汉测绘科技大学学报,1987,12(1):81-91.) |
| [20] | YUAN Yulei, JIANG Lixing, LIU Lingjie. Applications of Rodrigues Matrix in Coordinates Transformation[J]. Science of Surveying and Mapping,2010,35(2): 178-179.(原玉磊,蒋理兴,刘灵杰. 罗德里格矩阵在坐标系转换中的应用[J].测绘科学,2010,35(2):178-179.) |