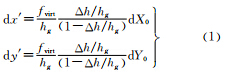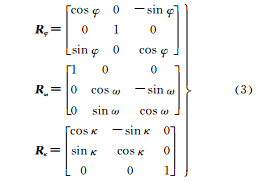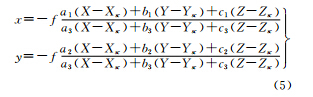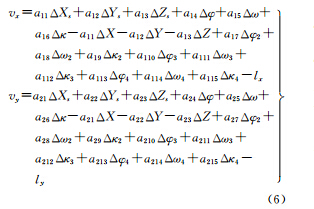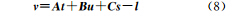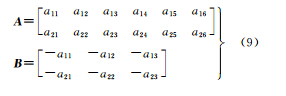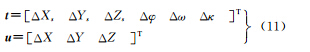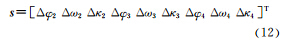1 引言
航空相机已在世界范围成功应用了几十年,在过去的20多年里,摄影测量的数据获取手段逐渐向数码相机的方向发展[1]。从目前的制造工艺和经济因素两方面考虑,单个数码相机还无法取代传统的胶片航空相机[2, 3]。为了采用更经济的手段满足大像幅航空摄影的需求,一些公司采用了多镜头组合相机。目前国际上主流的多镜头组合数码航空相机产品主要包括UltraCam系列大像幅数码航空相机,DMC大像幅数码航空相机[4],国内则有SWDC-4和TOPDC-4大像幅数码航空相机[5]。
TOPDC-4(以下简称四拼相机)基于这种原理,通过在平台上安装4个数码相机的方式,来获取具有大范围地面覆盖度的拼接影像。四拼相机的平台检校[6]就是准确获取相机与虚拟投影面之间相对位置关系的过程,根据平台检校参数可以从子影像生成高精度的虚拟影像。
平台检校是从子影像生成虚拟影像的关键步骤,只有准确知道了子影像与虚拟影像的相对外方位元素,才能根据投影变换公式,生成拼接后的虚拟影像。如果平台检校参数存在较大的误差,那么虚拟影像中的地物点将不能正确反映该点的空间位置关系。理论上位于重叠区的子相机间同名点在虚拟影像上完全重合;但实际上由于平台检校参数的误差,该点在虚拟影像的投影坐标会存在偏差,当这个偏差较大时,该点会存在较大的像平面误差,严重时重叠区虚拟影像甚至会出现错位的现象。
平台检校可以精确计算出子影像到虚拟影像的相对外方位元素,使拼接后生成的虚拟影像等效于一张高精度的中心投影影像[7],保证了影像数据源的精度。
目前的平台检校方法[6, 8, 9](有些论文从结果出发称之为影像拼接方法[10, 11, 12])基本上都是从子影像重叠区的匹配点出发,通过局部空三的方式,解算子影像间的相对位置关系。本文根据子相机相对位置关系在飞行时不发生变化这一前提,选取多个摄站的数据进行平台检校,扩大了匹配点的选择范围。并在空三过程中加以条件约束,弥补了当子影像重叠区范围较小,或重叠区影像纹理贫乏,无法匹配出理想数量且分布均匀的连接点时,无法准确计算出平台检校参数的不足之处。
2 现有平台检校原理分析
2.1 平台检校基本原理
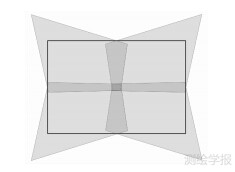
四拼相机采用外视场拼接的方式,将每台相机获取的子影像经投影变换到虚拟投影面,组合成大幅面影像,其外观及相机安装方式如图 1所示。如图 2所示,浅灰色区域为拼接后4个子相机的影像范围,深灰色区域为子相机间的重叠区,框内的区域为拼接后虚拟影像的裁切范围。

|
| 图 1 TOPDC-4外观及其安装方式 Fig. 1 TOPDC-4 and the configuration of sub-cameras |
为了生成高精度拼接影像,需要知道子影像与虚拟影像的相对位置关系。四拼相机中每台相机的安装位置和角度可根据设计值得到,但由于机械加工、设备安装精度等多种因素的影响,相机的实际姿态与理论值之间存在偏差。需通过平台检校,确定子影像与虚拟影像之间的相对位置关系(Xsc,Ysc,Zsc,φ,ω,κ)。
平台检校可以采用单组子影像十字重叠区匹配后进行空中三角测量的方式计算,也可以采用多组子影像全部参与匹配后空中三角测量的方式来计算。
|
| 图 2 影像拼接示意图 Fig. 2 Illustration of mosaic images |
2.2 虚拟影像的拼接误差分析
由于四拼相机是采用外视场拼接的方式,将每台相机获取的子影像经投影变换到虚拟投影面,组合成大幅面影像。当在重叠区地面有突起的建筑物或地形有较大起伏时,4个子相机之间由于构成立体基线会产生投影差,文献[7]分析了飞行高度、地形起伏对虚拟影像x、y方向产生的投影差。计算公式如下
式中,hg为航高;Δh为相对于地面的高差;fvirt为虚拟影像焦距;dX0为X方向子相机摄影中心到虚拟影像摄影中心之间的距离;dY0为Y方向子相机摄影中心到虚拟影像摄影中心之间的距离;dx′为虚拟影像中x方向的投影差;dy′为虚拟影像中y方向的投影差。
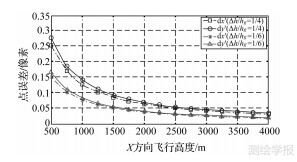
根据《数字航空摄影规范》[13],当地面分辨率大于20 cm时,航摄分区内的地形高差不大于1/4摄影航高;当地面分辨率小于或等于20 cm时,分区内的地形高差不大于1/6摄影航高。按照四拼相机虚拟影像焦距47 mm,像元尺寸6.8 um,计算可得dx′、dy′与Δh、Δh/hg的关系,如图 3。
计算分析可知,随着航高hg的增加,dx′和dy′减小;当hg=500 m、Δh/hg=1/4时,在Y方向的最大拼接误差达到0.276像素,对应于地面上只有1.997 cm,在X方向上更小;当hg=750 m、Δh/hg=1/4时,即地面点高于或低于参考面187.5 m时,最大拼接误差只有0.184像素,完全满足大比例尺成图精度要求。按照规范要求,Δh/hg的比值只有在极少的情况下超过0.2,而且在高差大的时候,规范规定的高程精度迅速放宽,拼接误差完全可以忽略不计[14]。
|
| 图 3 hg 与Δh/hg对dx′与dy′的影响 Fig. 3 Influences in dx′ and dy′ as a function of hg and Δh/hg |
2.3 十字重叠区方式平台检校及其存在的问题
平台检校可以采用同一时刻曝光的4张子影像,在十字形重叠区内匹配连接点,进行光束法平差。该方法利用重叠区的连接点进行计算,以其中1个相机为基准,计算其余3个相机与虚拟影像之间的相对外方位元素。文献[6]中对这种方法进行了详细的说明。
该方法计算量小且方法简便,但要求在4张子影像的重叠区有分布均匀的连接点,且数量不少于30~50个。当子影像重叠区范围较小,或重叠区影像纹理贫乏,无法匹配出理想数量且分布均匀的连接点时,该方法无法准确计算出平台检校参数。
2.4 传统光束法原理及其在平台检校中的问题
光束法区域网空中三角测量的运算是以每条空间光线为一单元,利用三点共线条件列出误差方程式[15]求解。采用航向重叠度80%,旁向重叠度60%的检校场多幅拼接影像,利用它们的子影像进行匹配,空三计算后可以得出每张子影像的外方位元素。理论上,根据同一时刻曝光的4张子影像的外方位元素,可以确定4台相机的相对位置关系,进而计算平台检校参数。但实际上,通过光束法求得的子影像外方位元素(Xsc,Ysc,Zsc,φ,ω,κ)中,由于线元素(Xsc,Ysc,Zsc)与角元素(φ,ω,κ)存在相关性,使得同一时刻拍摄的子影像线元素差异远超出了实际物理尺寸。以3组子影像空三加密结果的线元素为例。
| 影像编号 | 子相机编号 | X | Y | Z | 相机距离 | 备注 |
| 437 | ||||||
| 1 | 2 443.949 3 | 440.260 0 | 974.830 8 | 0.885 2 | 1、2相机 | |
| 2 | 2 444.376 5 | 439.951 6 | 974.119 5 | 1.009 3 | 2、4相机 | |
| 3 | 2 443.933 3 | 439.858 9 | 975.081 0 | 0.473 0 | 1、3相机 | |
| 4 | 2 444.598 5 | 439.908 7 | 975.103 1 | 0.667 4 | 3、4相机 | |
| 438 | ||||||
| 1 | 2 450.569 7 | 234.565 5 | 975.601 0 | 0.929 1 | 1、2相机 | |
| 2 | 2 451.024 5 | 234.234 3 | 974.861 6 | 0.917 2 | 2、4相机 | |
| 3 | 2 450.511 3 | 234.182 9 | 975.787 6 | 0.429 7 | 1、3相机 | |
| 4 | 2 451.178 8 | 234.248 0 | 975.765 6 | 0.671 0 | 3、4相机 | |
| 439 | ||||||
| 1 | 2 453.662 6 | 26.004 3 | 978.711 1 | 0.874 9 | 1、2相机 | |
| 2 | 2 454.121 3 | 25.763 9 | 978.006 0 | 0.880 4 | 2、4相机 | |
| 3 | 2 453.655 8 | 25.650 5 | 978.879 7 | 0.392 0 | 1、3相机 | |
| 4 | 2 454.283 5 | 25.682 3 | 978.867 5 | 0.628 6 | 3、4相机 |
根据相机的实际安装尺寸,两个子影像的摄影中心距离不超过0.15 m,而计算结果却与实际情况不符,这就是由于线元素与角元素相关而引起的。为了满足最小二乘的最优解,在计算的过程中过多地修正了线元素值。而且由于同一摄站获取的子影像间基线过短,线元素的稳定性也受到了很大影响。因此,不加限制条件直接计算子影像的外方位元素,推算出的平台检校参数并不能真实反映子相机间的实际位置关系。
3 附加约束条件的光束法原理
3.1 模型建立
3.1.1 线元素的约束
子相机安装到平台时采用高强度支架紧固,子相机间的距离几乎不会发生变化,可以看做一个整体,图 4

|
| 图 4 4个子影像与虚拟影像的投影关系 Fig. 4 Projection relationship between sub-image and virtual image |
通过地面检校场后方交会计算子相机的外方位元素时,会出现角元素解不够稳定的现象,直接生成的拼接影像中能发现影像的接缝。但由于地面控制点距离摄站的距离仅约40 m,相对于空中摄影700 m的航高而言,同一摄站子相机间的地面摄影基高比变为空中摄影的约17.5倍。从试验数据中分析,子相机间的线元素差异趋于相对稳定,且接近设计值,多次测量的X、Y方向线元素标准差小于10 mm,Z方向线元素标准差小于5 mm,取多次测量的平均值作为子相机线元素。
空三解算时线元素与角元素存在相关性,线元素的微小偏差可以通过角元素进行补偿[9],综合考虑相机的物理结构,可以将子相机的摄影中心距离作为已知值,将平台检校参数作为一个整体进行解算,更符合相机安置的实际情况。这时需要计算的未知数是子相机的安装角度,即子影像外方位元素中的角元素[16]。
根据相机安置的物理结构,过4个子影像的摄影中心拟合一个平面M(如图 5所示),4个摄影中心的重心O可作为虚拟影像的摄影中心[6, 17],由于相机摄影中心位置相对稳定,以过O点平行于S1S3连线方向作为Y轴,建立右手坐标系O-XYZ,O-XYZ是一个建立4个子相机摄影中心线元素关系的一个辅助坐标系。4个摄影中心在O-XYZ中的平面坐标为已知值(Dai,Dbi)。

|
| 图 5 4个子影像的摄影中心与虚拟影像摄影中心的关系 Fig. 5 Relationship between the projection centers of sub-images and the projection center of virtual image |
摄影时4台子相机同步曝光,且摄影中心间距很小,可以认为4个摄影中心在O-XYZ中的Z坐标相等。实际上,由于机械安装及硬件自身结构的影响,子相机的摄影中心到平面M存在最大不超过10 mm的距离。将倾斜影像纠正为水平影像,理论上不会产生纠正误差[18, 19],下面以水平影像为例,来分析摄影中心Z方向取近似值带来的影响。
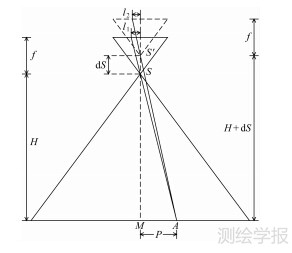
如图 6所示,相机焦距为f,航高为H,摄影中心为S,A为地面点。长度为P的地面线段MA在像平面的投影长度为l1,当S沿竖直方向平移dS至S′时,地面线MA在像平面的投影长度变为l2,可以计算dS引起的像点误差dlV=l1-l2=PfdSH+dS,其中l1=PfH,l2=PfH+dS。
|
| 图 6 摄影中心竖直方向位移引起的像点误差 Fig. 6 Image point error caused by vertical shift of projection center |
P为A点到摄影中心在地面 投影M的距离,四拼相机视场角约为96°×74°,则沿长边方向P的最大值为1.11H,沿宽边方向P的最大值为0.75H。当f=47 mm,H=700 m时,摄影中心竖直方向10 mm的误差在长边方向引起的像点误差约为0.52 um,在宽边方向引起的像点误差约为0.35 um,四角的像点误差最大值约为0.63 um,即最大像点误差不足0.1像素,且越靠近影像中心误差值越小。因此,子相机摄影中心到M的偏差对拼接影像的结果影响非常小,可以忽略不计[9],可以认为4个摄影中心在O-XYZ中的Z坐标相等,即Dz1=Dz2=Dz3=Dz4=0。
3.1.2 角元素的约束
理论上虚拟相机的焦距可以根据需要选择不同的值[17],为了减小虚拟影像与原始影像的比例尺差异,选择接近原始相机焦距的47 mm作为虚拟影像的焦距。
将平行于M并通过虚拟影像摄影中心所建立的坐标系作为虚拟影像的像空间辅助坐标系。计算4个子相机的角元素时,不能把角元素全部作为未知数,否则会出现自由度过大的情况,而是应该以一个相机作为基准(主相机),计算其他子相机(从相机)到这个相机的旋转角度[6]。同时虚拟面的旋转角也需要以主相机为基准,来确定子影像到虚拟面的旋转关系。
综合考虑,不妨以1号相机为作为主相机,将1号相机到虚拟面的旋转角设为一个初始的固定值,根据角元素的传递关系,其他子相机(从相机)相对于主相机的旋转角可以转换为从相机相对于虚拟面的旋转角,此时待求的平台检校参数实际为3个从相机的9个角元素。
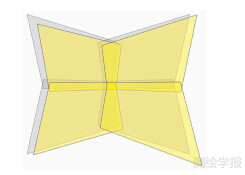
为了避免不同子相机与M平面的夹角差异较大,引起投影到虚拟影像后像元采样比例不平衡(图 7,灰色为对称分布的子影像投影范围,黄色为不对称分布的子影像投影范围),取4个子相机主光轴方向的几何平均作为虚拟相机的主光轴方向[17],计算时可以根据3个从相机的角元素修正量来调整主相机到虚拟面的旋转角固定值,使得4个子影像到虚拟影像的旋转角度尽可能对称。
3.2公式推导
根据前面的条件,子相机摄影中心在O-XYZ中的坐标为(Dai,Dbi,0)[4, 9],其中Dai、Dbi为已知值,设子影像在虚拟影像坐标系中的旋转角为(φi,ωi,κi),其中(φ1,ω1,κ1)为已知值,则子相机的摄影中心坐标(Xsc,Ysc,Zsc)为
|
| 图 7 子影像与虚拟影像夹角差异大引起的像元采样不平衡 Fig. 7 Unbalanced resample caused by the differences between sub-images and virtual image |
式中,R=RφRωRκ
式中,(φ,ω,κ)为虚拟影像的角元素;(XS,YS,ZS)为虚拟影像摄影中心线元素。
共线方程中,子影像对应的旋转矩阵为Rc=RRi,其中Ri=RφiRωiRκi
令Rc=a1a2a3b1b2b3c1c2c3,则共线方程可写为
由于Xsc、Ysc、Zsc可以用XS、YS、ZS的函数表示,对上式线性化以后得出误差方程式为
上式中各系数分别对应为
对于1号相机(φ1,ω1,κ1)为已知,相应的角元素偏导项为0,用矩阵符号表示的误差方程式为
式中
对于控制点,对应的ΔX、ΔY、ΔZ项为0。每组4个子影像对应一组系数矩阵A和未知数t,每个物方点对应一组u,每个子相机对应一组Δφi、Δωi、Δκi,s有3×3=9个未知数。关于偏导数的公式展开式较长,这里不详细列出。
考虑到虚拟影像与4个子相机的旋转角度(即平台检校参数)相关,而此时旋转角度为方程中的未知数,根据初值将1号相机影像至虚拟影像的旋转角度设为已知值,此时s中未知数变为9个。解算后根据2、3、4号相机旋转角度的修正值调整1号相机至虚拟面的旋转角,以使得虚拟影像与4个子影像的旋转角度对称。
将虚拟影像外方位元素A、物方点坐标B、子相机相对虚拟影像的旋转角C这些参数的初始值、以及每个观测点的像点坐标(xi,yi)代入方程迭代计算,直到结果收敛至阈值范围。
设有m组虚拟影像,n个观测点,p个物方点,q个控制点,则根据观测值可以列出2n个方程,其中有6m+3(p-q)+9个未知数,相对于传统的光束法平差增加了9个平台检校参数未知数,且在共线方程中引入了子相机的线元素常量(Dai,Dbi,0)和1号相机到虚拟影像的角元素常量(φ1,ω1,κ1)作为约束条件,这样解出的平台检校参数更符合子相机安装的实际情况。从以上的分析可以看出,这里的约束条件并不直接表现为增加条件方程[20],而是表现为已知量的代入,以及共线方程线性化中偏导系数的变化。
4 试验结果与分析
4.1 单相机检校及线元素的确定
目前单相机检校的理论与技术已相对成熟[21, 22],试验中单相机检校采用Australis软件进行处理。四拼相机采用Rollei量测型相机进行拼接,单相机像幅为7228像素×5428像素,焦距为47 mm,像元尺寸为6.8 um。单相机检校在中国测绘科学研究院内的地面检校场中进行,经Australis软件检校后像平面残差小于2 um。同时经过地面检校场检校后,得到4个相机安置的线元素物理尺寸为。
| Camera | Da | Db |
| 1 | 0.054 684 | -0.056 077 |
| 2 | -0.055 214 | -0.051 725 |
| 3 | 0.054 610 | 0.047 328 |
| 4 | -0.054 080 | 0.060 475 |
4.2 计算平台检校参数
平台检校参数采用四拼相机在河南登封检校场获取的飞行数据进行计算,对应的飞行航高为700 m,地面分辨率为10 cm,采用窄像对飞行方式,航向重叠度为80%,旁向重叠度为60%,基线长度为200 m。包含交叉分布的3条东西向航线和4条南北向航线,共计25张虚拟影像(100张子影像)。4个子相机安置角度的设计值见表 3,采用附加约束条件的光束法区域网平差对100张子影像进行平台检校,得到平台检校参数见表 4。
| Camera | φ | ω | κ |
| 1 | -22 | 18 | 0 |
| 2 | 22 | 18 | 180 |
| 3 | -22 | -18 | 0 |
| 4 | 22 | -18 | 180 |
| Camera | φ | ω | κ |
| 1 | -22.003 572 | 17.820 681 | 0.122 107 |
| 2 | 22.081 682 | 17.836 309 | 179.827 715 |
| 3 | -21.963 220 | -17.720 887 | 0.107 504 |
| 4 | 21.940 784 | -17.902 666 | 179.891 631 |
4.3 平台检校参数验证
平台检校参数验证采用同一架次飞行的数据,对应的飞行航高为700 m,地面分辨率为10 cm,采用窄像对飞行方式,航向重叠度为60%,旁向重叠度为35%,基线长度约为400 m。包含3条东西向航线,每条航线13张虚拟影像。将平台检校参数代入TopMosaic影像拼接程序,每个曝光点的4张子影像生成1张虚拟影像,每张虚拟影像像幅为15 400像素×10 400像素,像元尺寸为6.8 um,焦距为47 mm。然后将拼接后的39张虚拟影像采用数字摄影测量系统DPGrid进行空中三角测量,计算后得到表 5。
| mx/m | my/m | mz /m | 平面点数 | 高程点数 | 高程相对精度 | |
| 定向点 | 0.035 | 0.052 | 0.066 | 24 | 24 | 1/10 606 |
| 检查点 | 0.059 | 0.065 | 0.106 | 70 | 70 | 1/6604 |
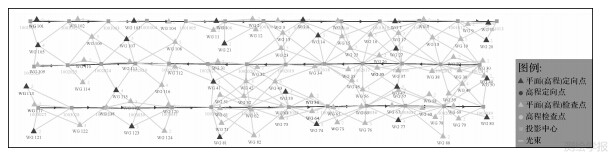
|
| 图 8 地面控制点及检查点分布情况 Fig. 8 Distribution of ground control points and check points |
从表 5中可以看出,高程中误差几乎与地面分辨率相当,检查点的高程相对中误差达到了1/6604,而且约0.088 m的平面中误差和0.106 m的高程中误差完全符合《数字航空摄影测量 空中三角测量规范》对大中成图比例尺基本定向点、检查点的限差要求[23]。这表明四拼相机虚拟影像的拼接误差小,平台检校参数计算结果精度高。
5 结 论
附加约束条件的光束法区域网平差,在传统光束法平差的基础上增加了针对四拼相机特定结构的约束条件,将四个子相机的平台检校参数作为一个整体进行解算,从而使平台检校参数更符合相机的实际安置情况。该方法为四拼相机以及同类多镜头组合相机的平台检校提供了一种新的思路,有助于在子影像间重叠度较小或重叠区匹配点少的情况下生成高精度的虚拟影像,以满足数据生产需求。
| [1] | MADANI M, DRSTEL C, HEIPKE C, et al. DMC Practical Experience and Accuracy Assessment[C]//Proceedings of IAPRS.Istanbul:IAPRS, 2004: 396-401. |
| [2] | KARSTEN J. Geometric Handling of Large Size Digital Airborne Frame Camera Images[J]. Optical 3D Measurement Techniques, 2007(8): 164-171. |
| [3] | YOUNG J L, ALPER Y, OLGA M S. In-flight Camera Platform Geometric Calibration of the Aerial Multi-Head Camera System[C]// Proceedings of the Aerospace and Electronics Conference.[S.l.]:IEEE, 2010: 136-139. |
| [4] | LI Jian, LIU Xianlin, WAN Youchuan, et al. Generation of SWDC-4 Aerial Digital Camera Virtual Image[J]. Geomatics and Information Science of Wuhan University, 2008, 33(5): 450-453. (李健,刘先林,万幼川,等. SWDC-4数码航空相机虚拟影像生成[J]. 武汉大学学报:信息科学版,2008,33(5): 450-453.) |
| [5] | LI Junjie, GUAN Yanling, YANG Mengmeng, et al. Development of Digital Airborne Camera[J]. Science of Surveying and Mapping, 2013, 38(1): 54-56. (李军杰,关艳玲,杨蒙蒙,等. 数字航测相机的研究进展[J]. 测绘科学,2013,38(1): 54-56.) |
| [6] | WOLFGANG Z, CHRISTOPH D, KARSTEN J. Geometric Calibration of the DMC: Method and Result[C]//Proceedings of IAPRS.Denver:IAPRS, 2002: 324-333. |
| [7] | LIANG T, CHRISTOPH D, KARSTEN J, et al. Geometric Accuracy Potential of the Digital Modular Camera[C]// Proceedings of ISPRS.Amsterdam:ISPRS, 2000. |
| [8] | ZHU Xiange, LI Yingcheng, LIU Xiaolong, et al. Analysis of Two Platform Calibration Methods of Multi-head Camera[J]. Remote Sensing Information, 2012, 27(4): 71-74. (朱祥娥,李英成,刘晓龙,等. 大幅面拼接航摄仪的两种平台检校方法分析[J]. 遥感信息,2012,27(4): 71-74) |
| [9] | HELMUT H , MICHAEL K , WOLFGANG Z . Calibration of the Digital Modular Camera[C]//Proceedings of FIG XXII International Congress. Washington :FIG,2002. |
| [10] | LI Jian, LIU Xianlin, LIU Fengde,et al. Mosaic Model of SWDC-4 Large Format Aerial Digital Camera and Accuracy Analysis of Stereo Mapping[J]. Science of Surveying and Mapping, 2008, 33(2): 104-106. (李健,刘先林,刘凤德,等. SWDC-4大面阵数码航空相机拼接模型与立体测图精度分析[J]. 测绘科学,2008,33(2): 104-106.) |
| [11] | CHEN Zhen, LI Jun, SU Guozhong. Technique of Digital Camera Image Joint[J]. Urban Geotechnical Investigation & Surveying,2006(5): 44-46. (陈镇,李军,苏国中. 数码相机影像拼接技术[J]. 城市勘测,2006(5): 44-46.) |
| [12] | LIU Fengying, WANG Dong. The Self-stablized and Dual-combined Camera Image Mosaic Technology[J]. Bulletin of Surveying and Mapping, 2012(1): 56-58. (刘凤英,王冬. 自稳定双拼相机影像拼接技术[J]. 测绘通报,2012(1): 56-58.) |
| [13] | Standardization Administration of the People’s Republic of China. GB/T 27920.1-2011. Specifications for Digital Aerial Photography-Part 1: Frame Digital Aerial Photography[S].Beijing:China Zhijian Publishing House,2011. (中国国家标准化管理委员会.GB/T 27920.1-2011.数字航空摄影规范第1部分:框幅式数字航空摄影[S] .北京:中国质检出版社,2011.) |
| [14] | WU Wenjing. Image Joining and Processing Technology Study of SWDC Aerial Digital Camera[D].Jiaozuo:Henan Polytechnic University, 2008. (吴文静. SWDC航空数码相机的影像拼接与处理技术研究[D]. 焦作:河南理工大学,2008.) |
| [15] | WANG Zhizhuo. Principle of Photogrammetry[M]. Wuhan:Wuhan University Press, 2007: 134-138. (王之卓. 摄影测量原理[M]. 武汉:武汉大学出版社,2007: 134-138.) |
| [16] | CHRISTOPH D, KARSTEN J, DIRK S. DMC-Photogrammetric Accuracy-Calibration Aspects and Generation of Synthetic DMC Images[J]. Optical 3-D Measurement Techniques VI, 2003(1): 74-82. |
| [17] | WU Dun. Geometric Aspects of Large Size Digital Frame Cameras and Their Use for Photogrammetric Data Acquisition[D]. Hannover: Leibniz University, 2007. |
| [18] | ZHANG Zuxun. Aspects on Aerial Digital Cameras[J]. Engineering of Surveying and Mapping, 2004, 13(4): 1-4. (张祖勋. 航空数码相机及其有关问题[J]. 测绘工程,2004,13(4): 1-4)) |
| [19] | WANG Hui, WU Yundong, ZHANG Yongsheng. Modeling and Analyzing of Geometric Joint Error for CCD Matrix Images of Digital Aerial Camera[J]. Journal of Institute p> of Surveying and Mapping, 2003, 20(4): 257-262. (王慧,吴云东,张永生. 面阵CCD数字航测相机影像几何拼接误差模型与分析[J]. 测绘学院学报,2003,20(4): 257-262.) |
| [20] | ZHENG Shunyi, HUANG Rongyong, GUO Baoyun, et al. Stereo-camera Calibration with Restrictive Constraints[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6): 877-885. (郑顺义,黄荣永,郭宝云,等. 附加约束条件的立体相机标定方法[J]. 测绘学报,2012,41(6): 877-885.) |
| [21] | LIN Zongjian, CUI Hongxia, SUN Jie, et al. Research on the Digital Camera Distortion Calibration[J]. Geomatics and Information Science of Wuhan University, 2005, 30(2): 122-125. (林宗坚,崔红霞,孙杰,等. 数码相机的畸变差检测研究[J]. 武汉大学学报:信息科学版,2005,30(2): 122-125.) |
| [22] | ZHANG Jianxia, WANG Liuzhao, LIU Xianlin, et al. Camera Calibration for Digital Air Survey[J]. Bulletin of Surveying and Mapping, 2005(11):41-42. (张建霞,王留召,刘先林,等. 数字航空摄影测量的相机检校[J]. 测绘通报,2005(11):41-42.) |
| [23] | Standardization Administration of the People’s Republic of China.GB/T 23236-2009.Specifications for Aerotriangulation of Digital Aerophotogrammetry[S]. Beijing:China Zhijian Publishing House,2009. (中国国家标准化管理委员会.GB/T 23236-2009.数字航空摄影测量空中三角测量规范[S]. 北京:中国质检出版社,2009.) |