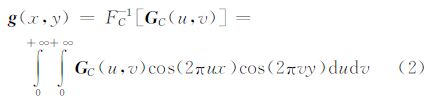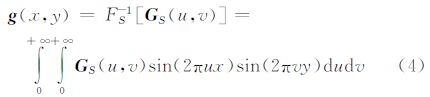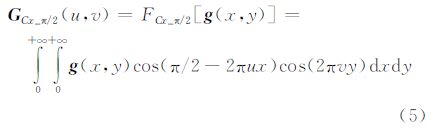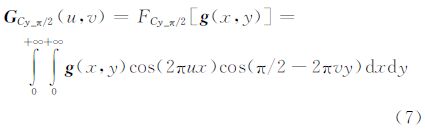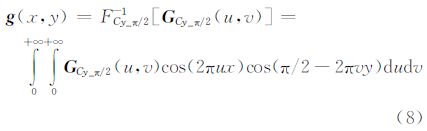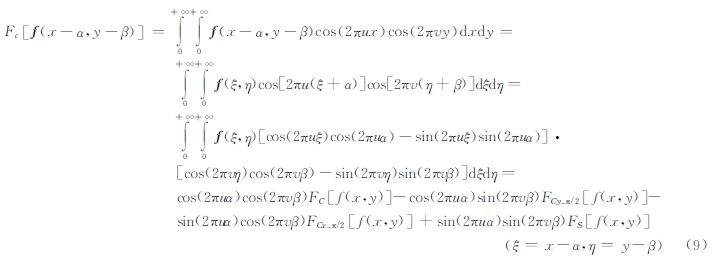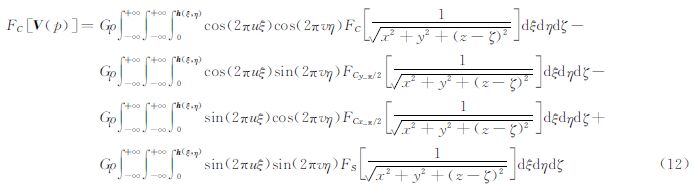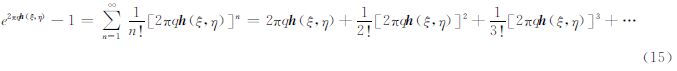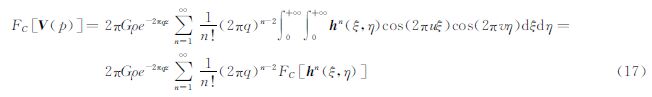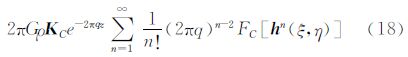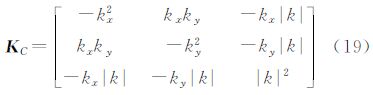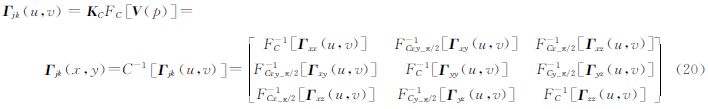1 引 言
在重力异常目标探测和物性反演问题中，重力梯度参数可更多地反映场源特征与细节，提高场源的分辨率，因此建立高精度全张量重力梯度数据库将有助于对地质勘探、全球重力场测定和辅助惯性导航等相关领域进行更深入的研究[1, 2, 3]。现阶段大范围高精度重力梯度数据实际测量需要大量人力、物力和时间，利用高精度数字高程模型(digital elevation model,DEM)和重力数据来正演重力梯度数据的方法是基准梯度数据库构建研究中现实而有效的途径[4, 5]。
重力梯度数据理论正演可分为空间域和频率域两种方法[6, 7]。文献[8]以棱柱法为基础提出利用高分辨率DEM计算重力梯度数据的方法，并分析了积分半径、高程误差等因素对计算精度的影响。棱柱积分等空间域正演方法是将所有单个体元对某点重力梯度的贡献累加计算，计算速度较慢，因此不适用于大规模实时正演数据。
频率域中快速傅里叶变换(fast fourier transform,FFT)是重力位场转换的常用方法，文献[9]利用傅里叶变换的卷积定理推导出重、磁位场的频域公式；文献[10]给出利用地形高程数据正演重力场异常的傅里叶变换公式；文献[11]将Parker方法由常密度模型推广到线性密度模型和指数密度模型；文献[12]分析了Parker方法正演重力梯度过程中密度误差对正演精度的影响；文献[13]深入研究了DEM正演重力梯度的频率域方法，并与空间域方法进行了比较。频率域方法利用快速傅里叶变换处理大规模网格数据，可一次性完成高分辨率DEM的正演计算，然而由于边界上不连续，通常会产生Gibbs 边界效应[14, 15]。因此常采用对网格数据扩边或滤波处理的方法来降低边界误差，但却增加了数据处理负担与计算复杂度[16]。文献[17]提出利用离散余弦变换(discrete cosine transform,DCT)计算重力异常导数的方法。本文研究并明确给出各种二维连续正、余弦变换定义及其时域平移特性，并根据定义和特性推导出利用高精度DEM数据正演全张量重力梯度数据的余弦变换Parker正演公式。
2 正、余弦变换定义及其时域平移特性正、余弦变换定义可分别由奇、偶函数的傅里叶变换推导得出，与傅里叶变换相比，余弦变换具有更高的能量压缩性能，在一阶马尔科夫过程中依据最小均方误差原则最接近Karhunen-Loeve变换性能[18]。下面给出二维连续正、余弦变换的定义以及时域平移特性。
2.1 二维连续正、余弦变换定义定义 1：如果二元函数g(x,y)在x,y∈[0,∞)定义区间满足傅里叶积分收敛条件［19]，则其二维连续余弦变换及其逆变换定义为
式中，u、v分别是在x、y方向上的空间频率；空间频率的函数GC(u,v)称为函数g(x,y)的二维余弦频谱密度函数。
定义 2：如果二元函数g(x,y)在x,y∈[0,∞)定义区间满足傅里叶积分收敛条件［19]，则其二维连续正弦变换及其逆变换定义为
定义 3：x方向上移相π/2的二维连续余弦变换及其逆变换定义为
定义 4：y方向上移相π/2的二维连续余弦变换及其逆变换定义为
2.2 二维连续余弦变换时域平移特性证明
文献[20]给出了一维连续余弦变换的定义及其时域、频域特性证明，同理这些特性可推广适用于二维连续余弦变换，其时域平移特性证明如下
3 基于余弦变换的Parker方法及应用 3.1 Parker正演方法余弦变换表达式推导
常密度质量分布的三度体Ω(ξ,η,ζ)在空间任一点p(x,y,z)处产生的引力位为
式中，G为万有引力常数；ρ为质量体密度，
；dV=dξdηdζ；假设质量体仅在参考平面(ξ≥0,η≥0)内存在质量分布，高程分布函数为ζ=h(ξ,η)。
对式(10)进行余弦变换可得
由于公式(11)中|r－r0|在时域的x轴和y轴上含有ξ,η平移分量，利用公式(9)证明的二维余弦变换时域平移特性可将式(11)化简为
由函数的奇偶性可知，上式后三项函数积分为零，且
为偶函数，根据被积函数的奇偶性很容易证明其傅里叶变换与余弦变换相同，文献[21]给出其傅里叶变换积分公式为
由于函数e2πqh(ξ,η)－1的泰勒级数展开形式为
则式(14)可化简为
由于高程分布函数ζ=h(ξ,η)仅在参考平面(ξ≥0,η≥0)内存在数值变化，则上式中的积分区间可转换为[0,+∞)，利用连续余弦变换定义1，可得基于余弦变换的Parker正演公式为
3.2 Parker方法正演全张量重力梯度
由于实际测量地形高程数据多以网格形式存储，因此在Parker正演公式中引入离散余弦变换。文献［22]于1974年给出序列长度为N的离散信号x(n)的一维离散余弦变换(DCT-Ⅱ)的定义，并在图像数据压缩等领域广泛应用。文献[17]推导出重力位场的余弦谱计算公式，并利用二维离散余弦变换实现了重力异常导数的计算。全张量重力梯度为引力位的二阶导数，与傅里叶变换计算重力梯度方法相似[12]，由余弦变换时域微分定理及移相π/2的时域微分定理，可得基于余弦变换的Parker方法正演全张量重力梯度频率域数学模型如下
式中，Γjk(j=x,y,z;k=x,y,z)分别对应各自方向的梯度张量，且有 式中，kx、ky分别为x、y方向上的波数，kx=2πu，ky=2πv;|k|=2πq=ikz且
对式(18)进行二维离散余弦逆变换或移相π/2的离散余弦逆变换，可进一步得到全张量重力梯度数据的空间域结果
为利用式(20)实现DEM数据正演梯度数据，下面给出移相π/2的二维离散余弦逆变换具体形式
式中,u∈{0,1,…,M－1}、v∈{0,1,…,N－1}，且归一化加权系数αu、αv定义为 4 仿真试验分析
美国国家地球物理数据中心(National Geophysical Data Center，NGDC)网站最高可提供3″×3″地形数据供用户下载。仿真试验中采用了如图 1所示的某区域海底地形数据，数据分辨率均为15″，数据维数481×481，覆盖范围2°×2°，DEM数据统计如表 1所示。
| m | ||||
| 特征参数 | 最大值 | 最小值 | 平均值 | 标准差 |
| -87 | -4 293.3 | -1 626.4 | 585.6 | |
在空间域正演方法中，域棱柱积分法利用数字高程模型数据以若干小棱柱体为地形单元模型，积分计算地形对测量点的全张量重力梯度中各个分量值的扰动影响[23]。棱柱法推理严格，精度较高，因此本文将频域Parker正演方法与棱柱积分方法进行比较分析。试验选取如下正演条件：重力梯度测量点高程取水准面，岩石密度ρc=2.67 g/cm3，海水密度ρw=1.027 g/cm3，积分半径r=30′。利用棱柱法正演梯度数据时，图 1所示DEM数据中距边缘30′以内的网格点因数据不足，不能满足积分半径要求，没有正演结果。为与频域Parker正演方法对比，选取图 1虚线方框中心区域范围：经度为0°35′E～1°25′E，纬度为0°35′N～1°25′N，维数200×200的数据进行正演试验分析。
|
| 图 1 仿真正演区域DEM数据 Fig. 1 DEM area data used in emulation forward computation |
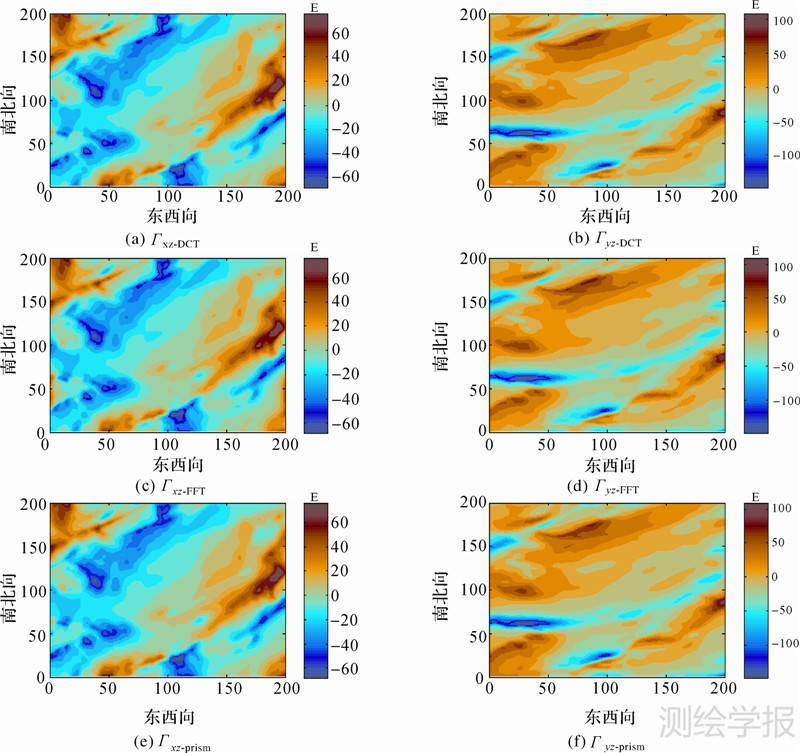
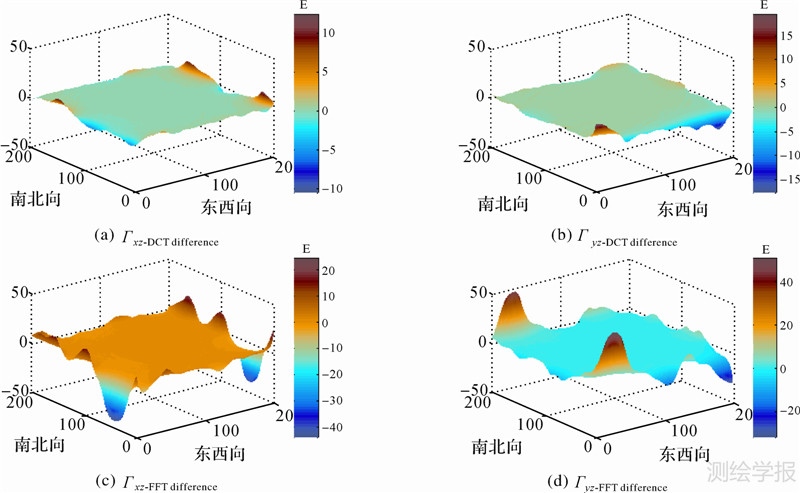
由于篇幅所限，图 2仅给出棱柱积分法、频域傅里叶变换法和余弦变换法正演所得的重力梯度张量Γxz和Γyz分量，其中两种频域方法泰勒展开阶数均为20阶。图 3是以棱柱法为参照，DCT和FFT两种Parker公式正演方法的相对数据误差图。从图中分析可知：① 3种正演方法获得全张量重力梯度Γxz和Γyz分量模型轮廓和数据范围相似，从而验证本文提出的余弦变换Parker正演公式的正确性；② 试验中两种Parker公式正演方法均未采取对DEM数据扩边或滤波处理，因此图 3中边界处虽然存在Gibbs效应产生的边界误差，但是余弦变换偶延拓的特性大大减小了这种误差。表 2中列出3种方法试验获得数据及其误差统计，从梯度数据的统计信息可知在本文仿真条件下3种方法整体上数据统计相近，但误差统计信息表明余弦变换Parker正演方法具有更高的精度，与傅里叶变换方法相比误差减小了3 dB左右。
|
| 图 2 DCT、FFT频域Parker方法以及棱柱积分法正演重力梯度数据 Fig. 2 Gravity gradients calculated by rectangular prism integration method and DCT,FFT frequency Parker’s method |
|
| 图 3 DCT、FFT频域Parker方法正演重力梯度数据误差 Fig. 3 The data error of gravity gradient calculated by DCT and FFT frequency Parker’s forward method |
| 梯度分量 | 测点数 | 最小值(E) | 最大值(E) | 绝对均值(E) | 标准差(E) | 误 差 (E) | ||
| 最大误差 | 平均绝对误差 | 均方根误差 | ||||||
| Γxz-Prism | 200×200 | -66.694 0 | 75.476 2 | 16.206 5 | 21.189 0 | -- | -- | -- |
| Γxz-DCT | 200×200 | -67.205 6 | 74.990 9 | 15.955 3 | 20.871 0 | 12.443 8 | 0.446 8 | 1.051 3 |
| Γxz-FFT | 200×200 | -67.116 3 | 74.475 9 | 15.910 0 | 20.748 9 | 43.903 3 | 1.012 2 | 3.244 1 |
| Γyz-Prism | 200×200 | -146.593 1 | 107.138 4 | 20.315 0 | 28.030 3 | -- | -- | -- |
| Γyz-DCT | 200×200 | -147.187 3 | 108.921 7 | 20.117 2 | 27.847 4 | 19.420 8 | 0.525 6 | 1.397 5 |
| Γyz-FFT | 200×200 | -147.089 2 | 101.419 1 | 19.757 4 | 27.478 0 | 50.631 3 | 1.136 2 | 3.604 8 |
实际应用中棱柱积分法选择不同的积分半径以及DEM网格分辨率会对地形数据正演的重力梯度计算精度和时间产生一定的影响[24]。积分半径越大，正演结果越精确，但计算量也随之递增，因此应用于较大区域时，若保证正演数据精度，其计算时间将变得不可接受。表 3将棱柱法和FFT法、DCT法的区域正演计算时间进行比较。其中正演区域网格数为481×481，使用2 GB内存，Pentium 2.7 GHz主频PC机，采用Matlab 2010作为仿真平台。分析结果表明，棱柱积分法计算速度慢，而频域方法则较好地满足了重力梯度数据快速实时正演的要求。其中虽然离散傅里叶变换是频域分析的有效工具，但它的变换核是复指数，采用FFT算法计算N×N点二维傅里叶变换可将计算复杂性降低到3/4N2log2N 次复数乘法和2N2log2N次复数加法运算，而一次复数乘法又需要4次实数乘法和2次实数加法，一次复数加法需要2次实数加法来完成，因此大量的复数计算成为算法中最耗时的部分。而离散余弦变换的变换核为实数，目前已有多种快速余弦变换算法可避免复数运算[25]，DCT-Ⅱ二维离散余弦变换计算复杂性仅为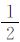
N2log2N次实数乘法和
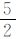N2log2N－2N(N－1)次实数加法运算。本试验中DCT算法只需进行实数运算，既减少了运算量又具有较好的推导算法，同时计算结果有较高的精度。
| 棱柱法 | FFT法 | DCT法 | |
| 网格数 | 481×481 | 481×481 | 481×481 |
| 计算时间 | 约4 h | 5.159 0 s | 3.983 7 s |
频域正演在处理大范围网格数据时体现出较好的速度优势，在重力异常地形改正等方面获得了广泛使用。因此本文以重力梯度实时快速正演为出发点，推导出基于余弦变换的频率域Parker正演公式。该方法的计算速度快，适用于实际应用中大量重力梯度数据的实时转换与处理，与傅里叶变换方法相比可有效减少边界效应引起的误差，具有较高的计算精度。
本方法在诸多领域拥有广阔应用前景，如更深入地研究密度参数对正演精度的影响，应用于变密度下的DEM正演重力梯度等问题；研究DEM和重力数据联合正演重力梯度的方法，从而获得更好的正演精度；还可广泛应用于重力梯度辅助定位中，以构建高精度基准梯度数据库，分析地形因素对重力辅助导航的影响。
| [1] | NABIGHIAN M N, ANDER M E, GRAUCH V J S, et al. Historical Development of the Gravity Method in Exploration[J]. Geophysics, 2005, 70(6): 63-89. |
| [2] | LI Shanshan, WU Xiaoping, ZHANG Chuanding, et al. Regional Quasi-geoid Refining Considering Corrections of Terrain and Complete Spherical Bouguer Anomaly's Gradient Term[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 510-516. (李姗姗,吴晓平,张传定,等. 顾及地形与完全球面布格异常梯度项改正的区域似大地水准面精化[J]. 测绘学报, 2012(4): 510-516.) |
| [3] | WANG Hubiao, WANG Yong, XU Daxin, et al. Distribution of Navigation Value about Vertical Gradient and Its Navigability Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 364-369. (王虎彪,王勇,许大欣,等. 重力垂直梯度导航值特征分布与可导航性分析[J]. 测绘学报, 2010, 39(4): 364-369.) |
| [4] | QIAN Dong, LIU Fanming, LI Yan, et al. Comparison of Gravity Gradient Reference Map Composition for Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 736-744. (钱东,刘繁明,李艳,等. 导航用重力梯度基准图构建方法的比较研究[J]. 测绘学报, 2011, 40(6): 736-744. |
| [5] | SHI Pan, WANG Xintao. Determination of the Terrain Surface Gravity Field Using Airborne Gravimetry and DEM[J]. Acta Geodaetica et Cartographica Sinica, 1997, 26(2): 117-121. (石磐,王兴涛. 利用航空重力测量和DEM确定地面重力场[J]. 测绘学报,1997, 26(2): 117-121.) |
| [6] | NAGY D, PAPP G, BENEDEK J. The Gravitational Potential and Its Derivatives for the Prism[J]. Journal of Geodesy, 2000, 74(7-8): 552-560. |
| [7] | TZIAVOS I N, SIDERIS M G, FORSBERG R, et al. The Effect of the Terrain on Airborne Gravity and Gradiometry[J]. Journal of Geophysical Research, 1988, 93(B8): 9173-9186. |
| [8] | DRANSFIELD M, ZENG Y. Airborne Gravity Gradiometry: Terrain Corrections and Elevation Error[J]. Geophysics, 2009, 74(5): 137-142. |
| [9] | GUNN P J. Linear Transformations of Gravity and Magnetic Fields[J]. Geophysical Prospecting, 1975, 23(2): 300-312. |
| [10] | PARKER R L. The Rapid Calculation of Potential Anomalies[J]. Geophysical Journal of the Royal Astronomical Society, 1972, 31(4): 447-455. |
| [11] | FENG R. A Computation Method of Potential Field with Three-dimensional Density and Magnetization Distributions[J]. Acta Geophysica Sinica, 1986, 29(4): 399-406. (冯锐. 三维物性分布的位场计算[J]. 地球物理学报,1986, 29(4): 399-406.) |
| [12] | LIU Fanming, QIAN Dong, LI Yan, et al. Influences of Density Error on Gravity Gradient forward Results[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2010, 38(12): 89-93. (刘繁明,钱东,李艳,等. 密度误差对重力梯度正演精度的影响[J]. 华中科技大学学报:自然科学版, 2010, 38(12): 89-93.) |
| [13] | JEKELI C, ZHU L. Comparison of Methods to Model the Gravitational Gradients from Topographic Data Bases[J]. Geophysical Journal International, 2006, 166(3): 999-1014. |
| [14] | JEKELI C. Error Analysis of Padding Schemes for DFTs of Convolutions and Derivatives[R]. Columbus: Ohio State University, 1998. |
| [15] | XIONG Y, LIU D. Convergence of Fourier Series and Gibbs Phenomenon[J]. Engineering Journal of Wuhan University, 2001, 34(1): 69-71. (熊元新,刘涤尘. 傅里叶级数的收敛性与吉伯斯现象[J]. 武汉大学学报: 工学版, 2001, 34(1): 69-71.) |
| [16] | WANG Wanyin, QIU Zhiyun, LIU Jinlan, et al. The Research to the Extending Edge and Interpolation Based on the Minimum Curvature Method in Potential Field Data Processing[J]. Progress in Geophysics, 2009, 24(4): 1327-1338. (王万银,邱之云,刘金兰,等. 位场数据处理中的最小曲率扩边和补空方法研究[J]. 地球物理学进展, 2009, 24(4): 1327-1338.) |
| [17] | ZHANG Fengxu, MENG Lingshun, ZHANG Fengqin, et al. A New Method for Spectral Analysis of the Potential Field and Conversion of Derivative of Gravity-anomalies: Cosine Transform[J]. Chinese Journal of Geophysics,2006, 49(1): 244-248. (张凤旭,孟令顺,张凤琴,等. 重力位谱分析及重力异常导数换算新方法——余弦变换[J]. 地球物理学报, 2006, 49(1): 244-248.) |
| [18] | RAO K R, YIP P. Discrete Cosine Transform: Algorithms, Advantages, Applications[M]. Ann Arbor: Academic Press, 1990. |
| [19] | YE Qixiao, SHEN Yonghuan. Handbook of practical mathe-matics[M]. Beijing: Science Press, 2006.(叶其孝,沈永欢. 实用数学手册[M]. 北京: 科学出版社, 2006.) |
| [20] | BRITANAK V, YIP P C, RAO K R. Discrete Cosine and Sine Transforms: General Properties, Fast Algorithms and Integer Approximations[M]. Ann Arbor: Academic Press, 2007. |
| [21] | ERDELYI A. Tables of Integral Transforms[M]. New York: McGraw-Hill, 1954. |
| [22] | AHMED N, NATARAJAN T, RAO K R. Discrete Cosine Transform[J]. IEEE Transactions on Computers, 1974, 100(1): 90-93. |
| [23] | WU Lin, MA Ji, ZHOU Yao, et al. Modelling Full-tensor Gravity Gradient Maps for Gravity Matching Navigation[J]. Journal of System Simulation, 2009, 21(22): 7037-7041. (武凛,马杰,周瑶,等. 重力场匹配导航的全张量重力梯度基准图模拟[J]. 系统仿真学报, 2009, 21(22): 7037-7041.) |
| [24] | LI X, CHOUTEAU M. Three-dimensional Gravity Modeling in all Space[J]. Surveys in Geophysics, 1998, 19(4): 339-368. |
| [25] | CHO N I. Fast Algorithm and Implementation of 2-D Discrete Cosine Transform[J]. IEEE Transactions on Circuits and Systems, 1991, 38(3): 297-305. |