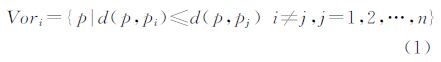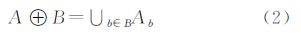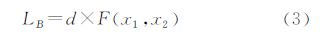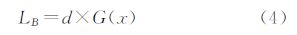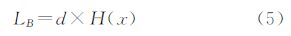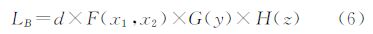1 引 言
Voronoi图在地理学中的应用早在GIS技术诞生之前便成为计量地理的重要的几何分析方法,在基础设施选址、功能设施服务范围划分、竞争性地理空间剖分、群点设施分布特征提取等方面发挥重要作用[1, 2, 3, 4, 5, 6]。GIS诞生后通过计算机技术的应用,Voronoi图在地理分析的作用得到进一步扩展,商业化的GIS软件(如ESRI的ArcGIS)将Voronoi图分析模块作为空间分析软件的主要功能之一。
Voronoi图的原理及建立的算法是基于空间距离的概念,基于不同的空间距离概念可建立不同的Voronoi图,常规的Voronoi图通过二维平面的欧氏距离或三维空间的球面距离建立[5, 6, 7]。在城市网络空间中,顾及设施点的服务功能及相互联系发生于网络路径而非传统的欧式距离,仍然采用欧氏距离进行空间分析是不合理的。对于像商场、幼儿园、消防站之类的服务设施通过基于欧氏距离的Voronoi图剖分计算其服务范围及空间剖分,忽略了城市空间通达、连接是沿着街道网的路径距离的事实[8, 9]。为此,文献[10]提出了网络空间Voronoi图概念。
平面Voronoi图需要转换到网络空间下,建立顾及网络路径代价的Voronoi图划分结构,即网络Voronoi图(N-VD)。对于平面Voronoi图,子多边形 Vori是依据欧式距离d来表示,它是基于平面空间是一个均质空间的理想假设,认为平面空间上任意两地之间可以直线到达,即采用直线欧氏距离来度量两地之间的距离。但是在网络环境下,由于空间联系约束条件的变化,各种地理要素的空间流动是沿道路网进行的,Voronoi图 的每个子网络Vori需要基于网络距离来划分[10, 11]。所以N-VD 是由一组子网络构成,即Vor={Vor1,Vor2,…,Vorn}。子网络Vori的表达式
式中,d(p,pi)为网络上任意点p和发生元pi间的网络最短路径距离。
网络Voronoi图可应用于多个领域,如交通事故分析、街道犯罪分布分析、物流、商业布局等的分析与规划[12, 13]。与采用欧氏直线距离的广义平面Voronoi图的粗略划分相比,广义网络Voronoi图是划分城市化区域功能服务域较为精确的方法,并定义了内敛型网络Voronoi图、扩展型网络Voronoi图、加权网络Voronoi图等6 种类型的广义网络Voronoi图,分别考虑了距离的有向性、权重差异与最短路径连接等约束条件[10]。文献[14]在评估城市零售商业需求的研究中考虑到道路通行能力差异约束的重要作用,在道路网络分析中用路径时间代替路径距离。文献[15]采用网络Voronoi图研究城市商业网点的市场域划分。文献[16]提出一种基于网络Voronoi面域图的最大覆盖选址模型及相应的粒子群优化方法,可以为城市化区域响应敏感型公共服务设施的空间优化提供技术方法。
在网络Voronoi图建立算法中,最常用的是基于图的最短路径算法 (以Dijkstra’s为代表),文献[10]给出了一种基于扩展最短路径树(ESPT)的构图算法,考虑了各种类型发生元(点、线、面等)、权重最短路径距离以及道路通行方向等条件下网络Voronoi图的生成办法。基于最短路径的网络Voronoi图生成算法难于负载约束条件,考虑到Voronoi图生成中的距离扩展思想在栅格数据结构下容易实现,受文献[17, 18]平面空间栅格化后通过数学形态学扩充算子实现Voronoi图生成的启示,本文提出网络空间基于栅格化距离扩展的Voronoi图生成算法,但在栅格化处理与扩充方式上具有网络空间固有的不同于欧氏平面空间的特点。欧氏空间栅格化处理的常用办法是利用一定尺寸的网格单元划分平面,栅格单元是向四方向或八方向领域扩展,网络图的拓扑关系在这样的划分体系内将被忽略;在网络空间中以弧段的细分单元段定义栅格,栅格单元是沿线性方向领域扩展,图的拓扑关系将被继承,这种扩展方式与水流沿管道线性方向蔓延的现象非常类似。引入水流扩展思想,将事件点发生源视为“水源”,以栅格单元长度为扩展步长,让水流方向沿着网络上的可通行路径同时向外蔓延,直至与其他水源的水流相遇或者到达边的尽头,提取网络图上各水源出发的水流覆盖的路径子集,便得到网络空间的Voronoi图几何构造。水流扩展的思想与文献[20]给出的网络空间下的区域生长方法类似,但本研究加强了3个扩充约束条件,考虑了发生元的几何类型(点、线、面等)、道路等级与通行能力以及路段通行方向等约束条件下的扩展类型。
2 网络图的栅格化本研究基于栅格扩展思想建立网络Voronoi图,首先对网络空间进行栅格化处理。栅格数据模型基于场的思想强调整体性、空间相关性特点,通过剖分的单元及其相互作用构建空间的联系,易于实现空间的序贯扩展。
欧氏空间的数据结构有矢量结构和栅格结构,在网络空间中,同样可以借鉴平面栅格化的思想,对网络图的边加密剖分,以边的细分单元段定义网络空间中的栅格,从而建立网络栅格数据结构。栅格剖分的长度可根据不同空间尺度下的应用背景来决定,如火车站的服务范围大于汽车站,算法实施中可用较大的距离阈值来剖分网络。
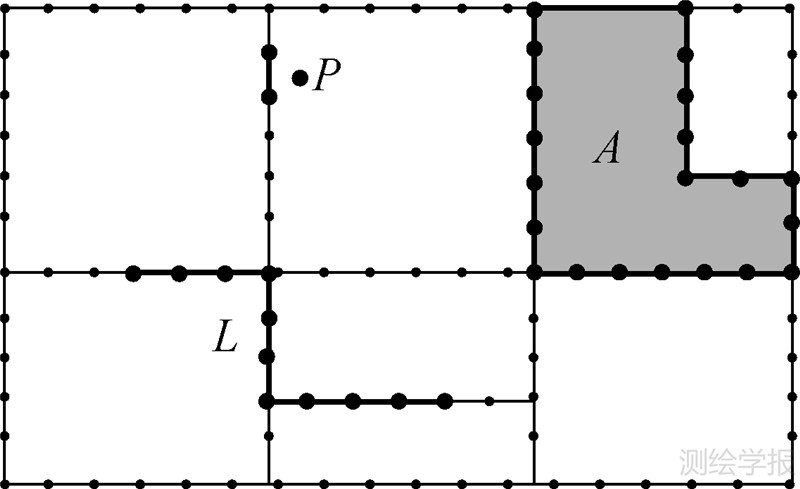
在栅格数据结构中,作为Voronoi图发生元的点、线、面等几何实体也通过栅格单元或栅格单元集表示。点实体表示空间覆盖面小,可忽略面积小的城市空间设施点,如ATM取款机,通过就近原则,将实体投影到网络空间的边上,所落入的栅格单元标记为点实体。线实体表示城市空间中的线状设施,如公共汽车线路,实体在网络上覆盖的栅格单元集标记为线实体。区域实体表示城市空间中闭合街道链组成的面状设施,如小学,实体边界覆盖的栅格单元集标记为区域实体。网络栅格单元可以标记多种实体类型,还有如表示连锁超市的点集实体,群点投影覆盖的栅格单元均标记为同一实体。图 1为网络和发生元点 P、线L、区域A的栅格化结果。
|
| 图 1 网络的栅格单元结构 Fig. 1 Raster cell structure of network |
网络边经栅格化后可定义3种类型标记:① 网络图中边的ID号;② Voronoi图发生元的ID号;③ 后继扩展中被发生元覆盖的栅格ID号。在后继栅格扩展中,将边上的栅格分为3种:对于已被发生元占用的栅格,若它邻接的栅格中有未被占用的栅格存在,称为C1类栅格即扩展栅格,其他已被发生元占用的栅格为C2类栅格;对于未被发生元占用的栅格,称为C3类栅格。边在栅格化之后,依据节点-边拓扑结构建立任意栅格单元的邻接关系,即位于边中段的栅格与栅格间的邻接关系;与节点邻接的栅格与节点间的邻接关系,则需要考虑映射到节点-栅格拓扑结构模式下,以方便后续的扩展操作。
3 基于水流扩展思想的网络Voronoi图生成这里引进水流扩展的原理构建网络Voronoi图,它类似于数学形态学中的区域膨胀原理,用具有一定形态的结构元素去度量和提取目标对应形状以达到对目标分析和识别的目的。区域膨胀的具体过程是:先对每个需要分割的区域找到原始种子像素作为生长起点,然后将种子像素和周围领域中有相同性质的像素合并到区域中,并将这些新像素当做新的种子继续上面的过程,直到没有满足条件的像素可以被包括到区域中。水流扩展算法可以理解为水流从网络上的所有水源栅格(事件发生元的扩展栅格位置)出发,沿着网络弧段同步向外蔓延,遇到网络交叉口便依据节点-边拓扑关系分散为不同支流继续扩展,直至网络边的尽头或遇到其他支流时结束。
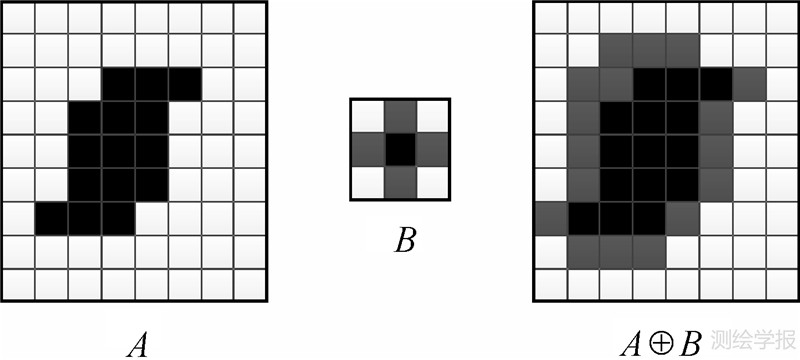
3.1 扩展操作Voronoi图的生成主要是边缘的变化,在栅格结构中,无论发生元是点、线还是区域,最终的操作单元都是栅格或栅格集,称这类边缘上的栅格为扩展栅格。基于节点-栅格拓扑结构,可以很方便地检索到扩展栅格在各自扩展方向上的邻接栅格,即新的扩展栅格,更新扩展栅格的位置,同时更新发生元的属性标记,得到Voronoi图新的边缘。设 A为原区域,B为基本结构元素,图 2给出了区域膨胀操作的基本过程[17],网络扩展的详细定义如图 3所示。水流扩展方法选用的结构元素为网络栅格,形态学运算采用网络扩展操作。区域膨胀操作可沿目标周围各方向执行,而网络扩展操作考虑了欧式平面的各向异性特征,扩展操作的执行路径只能是网络弧段。
|
| 图 2 平面栅格结构的区域膨胀操作 Fig. 2 Dilation operation based on raster structure of planar space |

|
| 图 3 网络栅格结构的扩展操作 Fig. 3 Dilation operation based on raster structure of network |
图 3中扩展操作的前提是假设道路是双向的、无等级之分且所有发生元的权重相同,所生成的常规网络Voronoi图的邻接子网络具有很好的对称性。但是在城市交通网络下,道路存在单双向限制、等级高低之分,另外事件发生元的属性有强弱差别,直接影响支流扩展速度和覆盖范围。考虑街道网络空间的实际条件,可通过负载扩展约束条件建立约束网络Voronoi图。
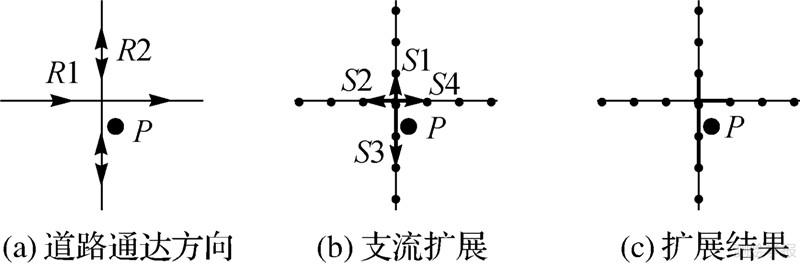
3.1.1 网络边通达方向约束将网络边通达方向纳入Voronoi图生成的限制条件中,判断当前支流扩展的方向与网络边的通达方向是否一致,如果二者不一致,则表明该支流是不能沿着该方向在弧段上扩展。例如图 4(a)中道路R1只能由西向东单向通行,支流S2的扩展方向与道路R1的方向相反,所以S2必须停止扩展,支流 S4的扩展方向与道路R1通行方向相同,支流S1、S3的扩展路径R2也是双向行驶路,因此支流S1、S3、S4可以继续执行扩展操作,图 4(c)为发生元P扩展一步的结果。式(3)表示的是支流在方向弧段上的扩展步长
式中,LB为基本结构元素B的长度;F(x1 ,x2)为二值函数(支流方向x1与弧段的通达方向x2一致时,函数值为1,否则为0);d为弧段上栅格单元的长度。
|
| 图 4 道路通达方向约束下的扩展 Fig. 4 Dilation operation under constraint of road’s direction |
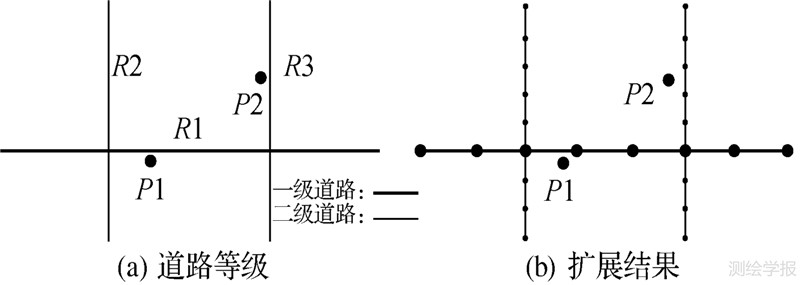
考虑到各等级道路通行能力的差异性,对不同等级道路链段设置不同的权重,道路上栅格单元即基本结构元素B的剖分长度按照公式(4)计算,例如图 5(a)中一级道路R1权重为2,二级道路R2、R3权重为1,如果道路R2、R3上栅格单元长度为LR,则R1上栅格单元长度应为 2LR。通过控制栅格单元的长度,R1上支流的扩展速度将是在其他道路上扩展速度的2倍,图 5(b)表示支流扩展一步长的结果。
式中,LB为基本结构元素B的长度;G(x)为道路的权重函数;d为权重值为1的道路上栅格单元的长度。
|
| 图 5 道路权重约束下的扩展 Fig. 5 Dilation operation under constraint of road’s weight |
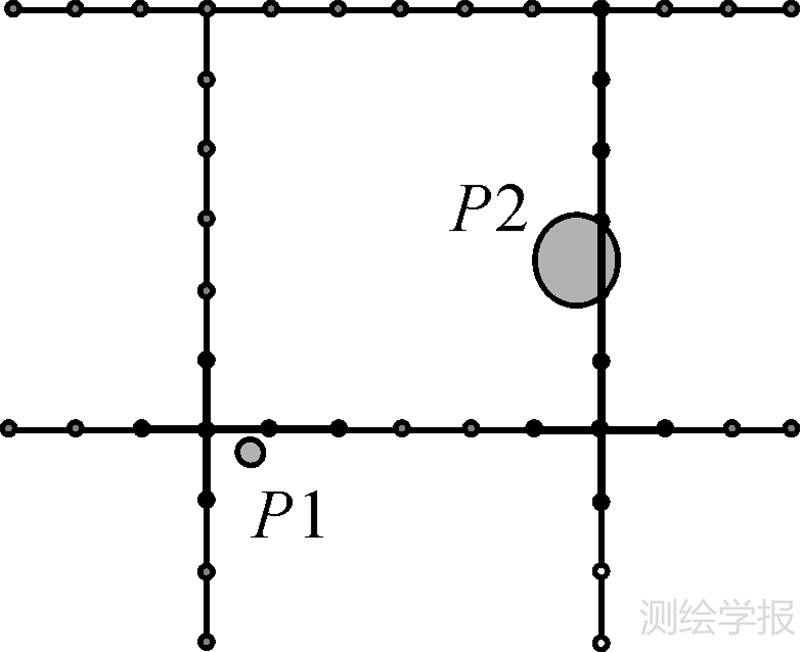
另外,在选择商场或者其他类型设施的时候,不仅要考虑空间距离,选择其中最近的设施,也需要综合考虑商场的规模、商品价格等影响顾客心理距离的发生元属性因素。所以在网络的栅格结构中,对于发生元的特征权重,算法规定以从该发生元出发的支流的初始传播速度即扩展一个步长(栅格数)来表示。如图 6中发生元P1、P2的权重分别为1和3,则从P1出发的支流向前扩展一个步长为一个栅格,P2扩展步长为3个栅格。公式(5)表示在扩展源权重条件下支流的扩展步长
式中,LB为基本结构元素B的长度;H(x)为发生元的权重函数;d为权重值为1的发生元在弧段上的扩展步长。
|
| 图 6 发生元权重约束下的扩展 Fig. 6 Dilation operation under constraint of source element’s weight |
综合以上3种约束条件,统一道路等级及发生元属性对扩展速度的贡献权重,则支流扩展步长的实际网络距离LB可以表示为
式中,d为权重值为1的弧段上栅格单元的长度;F(x1 ,x2)、G(y)、 H(z)分别为通行方向条件下的二值函数、道路和发生元的权重函数,其中函数F(x1 ,x2)的值由当前支流的扩展方向x1以及道路通行方向x2共同决定(支流方向x1与边的通达方向x2一致时,函数值为1,否则为0),另外道路等级y定义道路的权重函数,发生元的权重函数则根据地理实体的规模及商品价格等综合属性影响因子z来表示。
3.2 算法主要步骤及生成网络Voronoi图具体的Voronoi图生成算法如下:
(1) 首先对网络数据进行预处理,将所有道路交叉点和不同等级道路的分界点等特征点定义为网络节点,利用网络节点自动分割道路,生成网络弧段,然后将弧段等分为一定长度的基础线性单元集,这里称基础线性单元为网络栅格,建立网络节点-弧段拓扑关系以及网络栅格-栅格拓扑关系、网络节点-栅格拓扑关系,构建栅格数据结构。
(2) 将网络上离事件源欧式距离最近的栅格单元集定义为新的发生元,即初始化发生元,若发生元的邻近栅格属于C3类栅格,称这类发生元处于活跃状态,否则为死亡状态。
(3) 以所有活跃发生元为“水源”,“支流”从发生元标识的扩展栅格位置出发,沿着相应的扩展方向扩展一个步长,并且更新栅格标识属性,若“支流”的扩展栅格与其他“支流”的扩展栅格位置重叠或者到达网络的尽头时,就标识该“支流”处为枯竭状态。
(4) 判断发生元活跃与否,即检查由该发生元出发的所有“支流”是否都处于枯竭状态。
(5) 反复运行步骤(3)和(4),直至所有发生元均处于死亡状态。
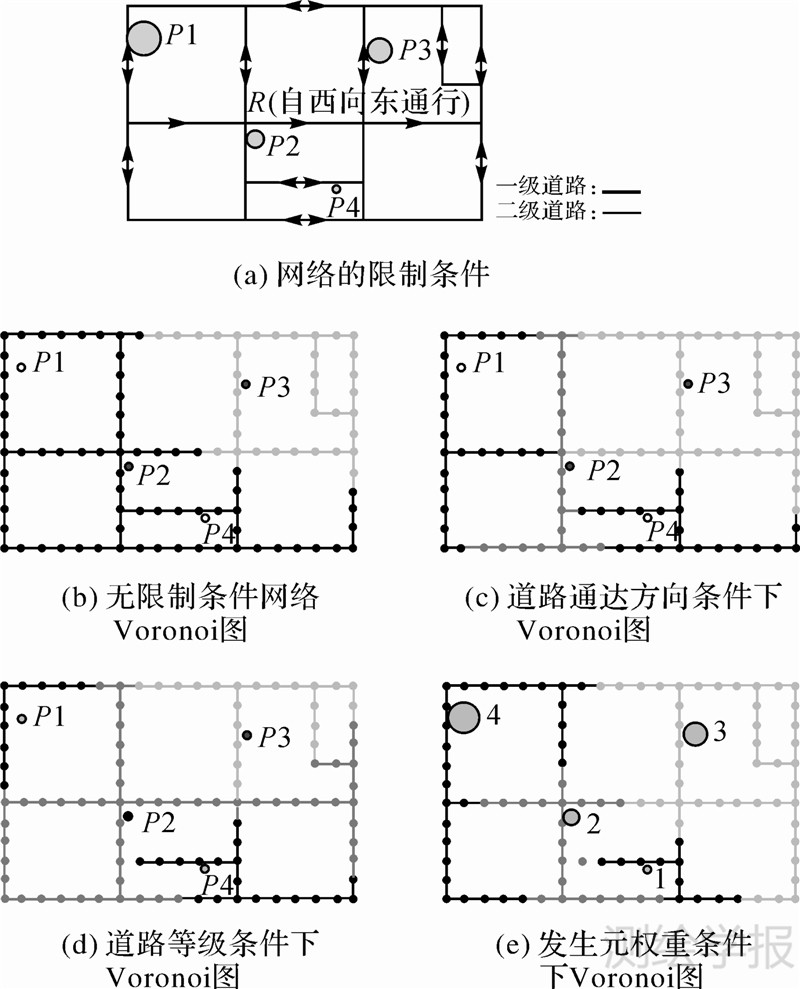
基于以上步骤,该算法生成的网络常规Voronoi图及加权Voronoi图的情况如图 7所示。
|
| 图 7 不同约束条件下的网络Voronoi图 Fig. 7 Network Voronoi diagrams under different constraints |
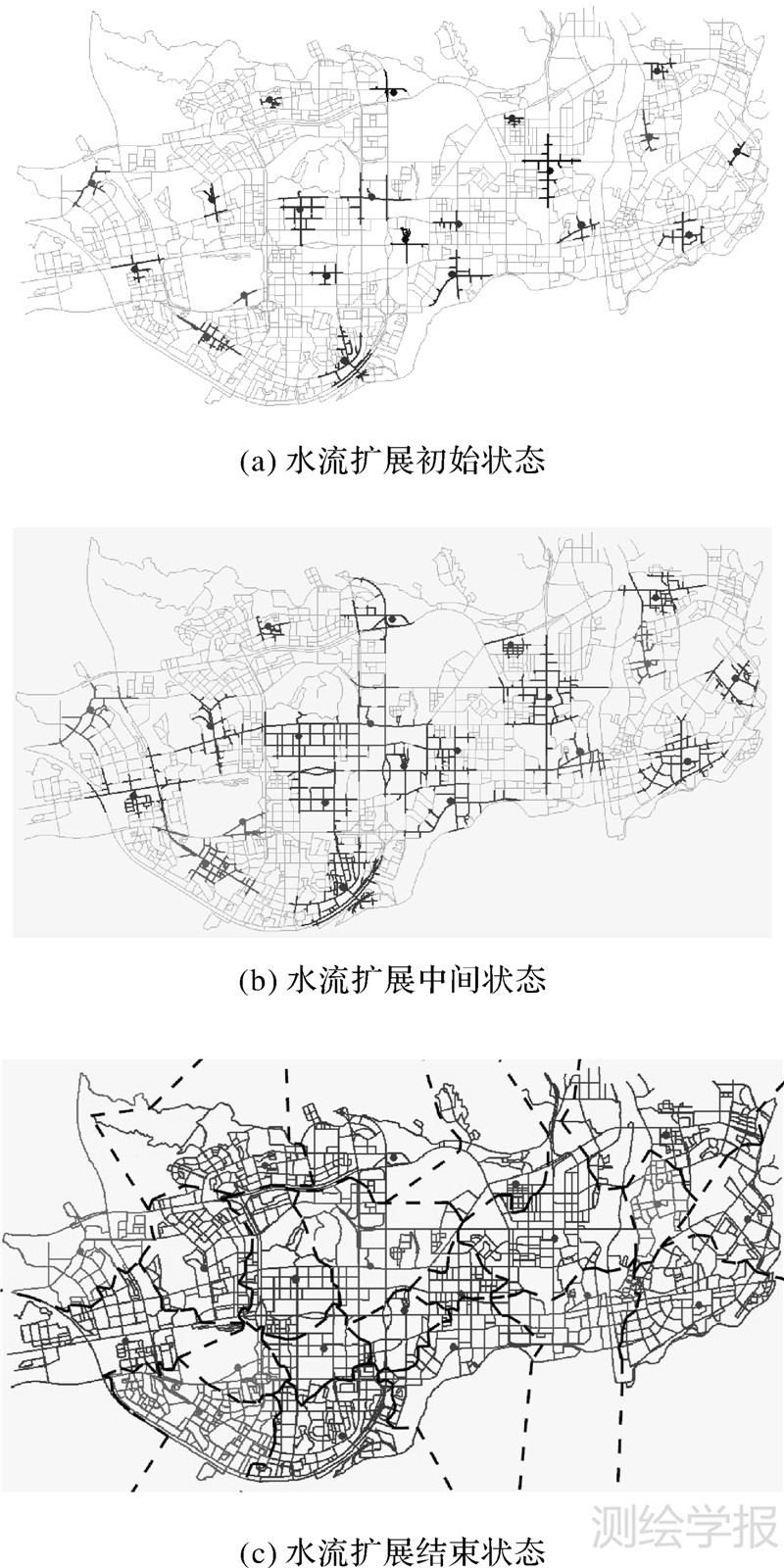
基于上述思想,本文采用VC++编程语言开发了网络Voronoi图生成的试验系统,在P8/2.5GB/2GB/Windows XP环境下对深圳市街道网某类型21个零售网点进行功能辐射域模拟。参与分析的道路网络由4167条道路链段组成,其中道路分为3级,参考各级道路的通行时速:主干道60 km/h、次干道40 km/h一般道路20 km/h,道路权重分别设为3.0、2.0、1.0,部分路段考虑方向限制。表 1给出了分别采用80 m、40 m、20 m、10 m、5 m 6种网络栅格剖分尺度提取的网络加权Voronoi图试验的算法性能参数(NWVD)。图 8为网络栅格剖分尺度为10 m时网络加权Voronoi图,若规定图 8(a)为水流扩展过程中的初始状态,图 8(b)为扩展中间状态,则按照由状态1至状态2的序贯扩展顺序,可以获得图 8(c)所示的扩展结束状态。
| 栅格剖分粒度/m | 剖分栅格数量 | 预处理时间/s | 分析构图时间/s | 构建NWVD总时间/s |
| 80 | 25 259 | 0.907 | 0.453 | 1.360 |
| 40 | 35 030 | 1.015 | 0.656 | 1.671 |
| 20 | 57 324 | 1.453 | 1.000 | 2.453 |
| 10 | 105 170 | 3.719 | 1.484 | 5.203 |
| 5 | 202 907 | 23.500 | 3.547 | 27.047 |
|
| 图 8 深圳市街道网某零售网点的网络加权Voronoi图生成过程 Fig. 8 Generation of weighted network Voronoi diagram of Shenzhen retail points |
从试验中可以看出,基于网络栅格结构和水流扩展思想生成的网络Voronoi图可以描述城市设施点在多种约束条件下的功能覆盖范围,通过空间竞争获得的网络子集与基于欧氏距离得到的空间划分有很大差别,如图 9中平面Voronoi图对网络的光滑切割及图 8所示的网络Voronoi图划分网络的锯齿状边界,这是因为区域内道路分布不均匀,路网密度不够,平面上任意两点之间没有直线道路通达。

|
| 图 9 基于平面欧氏距离Voronoi图 Fig. 9 The corresponding Voronoi diagram based on planar Euclidean distance |
本研究基于网络栅格的各向异性特征进行水流扩展计算,同时也利用索引进行邻接栅格单元的求取,算法的时间消耗在两个方面:第一个是在弧段的栅格剖分过程,假设有n条弧段,则剖分算法的时间复杂度为O(n);第二个是扩展过程,假设有m个设施点,则水流扩展算法的时间复杂度为O(m)。综合以上过程,算法的时间复杂度应为线性时间O(m+n)。由表 1可知,算法时间上的消耗主要与网络栅格的剖分粒度有关,剖分粒度从80 m细化到10 m过程中,预处理与扩展构图所需时间并没有太大差别,但是剖分粒度为5 m时,预处理的时间占用了算法时间的主要部分,并且算法时间复杂度随剖分粒度的细化呈近指数关系增长。因此在满足精度要求的条件下,可以调整网络栅格的剖分粒度来控制算法时间。
使用适当的栅格化单元大小可以在保证应用精度的同时减少计算时间。确定单元大小取决于以下几个因素:① 设施点的服务范围,例如火车站和长途汽车站的服务范围比公共汽车站的服务范围更大,可以使用较大的栅格单元;② 网络边的平均长度,网络中边的栅格化划分会导致每条边都产生一定的误差,而越短的边产生大误差的可能性越大,网络边的平均长度越大,栅格剖分粒度就越大;③ 设施点之间的距离,分散于网络中的设施点间的距离越大,栅格剖分粒度可以越大。在满足精度要求的情况下,基于网络最短路径的Voronoi图生成算法效率较高,同时可负载多种约束条件。
5 结 论本文以一种新的思想给出了网络Voronoi图的生成算法,并以深圳市POI为例进行了零售网点功能辐射域的模拟试验。通过算法设计与试验分析得出下面结论:
(1) 该Voronoi图生成的算法思想直观,可在多种约束条件下扩充,可与地理现象过程结合模拟地理过程演变,如人员、车流的输送扩散等[19]。
(2) 算法的时间主要取决于网络栅格剖分粒度,随着剖分粒度细化,时间消耗呈近指数关系增长。
(3) 算法可以生成网络常规Voronoi图和加权Voronoi图。网络Voronoi图既考虑地理实体的几何属性(如空间位置关系等),又充分考虑地理实体的非空间属性(如道路等级、综合实力等),这些特征使网络Voronoi图更有实际意义。
在实际应用中,为解决大数据量执行效益问题,可以借鉴栅格处理的分治办法或其他并行处理策略,分治法是常规的几何算法优化技术,本算法中可以利用空间切片将网络Voronoi图的生成分解为多个独立的扩展过程,合并切片时采用一致性处理技术维护切片边界的逻辑关系。
| [1] | GOLD C M.The Meaning of ‘Neighbour’[J]. Lecture Notes in Computing Science,1992(39):220-235. |
| [2] | GOLD C M. Advantages of the Voronoi Spatial Model[C]//Proceedings Eurocarto XII.[S.l.]: National Science Foundation,1994:1-10. |
| [3] | CHEN J,JIANG J. Locational Optimization of Point like Facilities through Voronoi Tessellation[C]//International Colloquium on Integration, Automation and Intelligence in Photogrammetry, Remote Sensing and GISs. Wuhan:[s.n.], 1994. |
| [4] | CHEN Jun, ZHAO Renliang,QIAO Chaofei.Voronoi Diagram Based GIS Spatial Analysis[J]. Geomatics and Information Science of Wuhan University,2003,28(sup):32-37.(陈军, 赵仁亮, 乔朝飞. 基于Voronoi图的GIS空间分析研究[J].武汉大学学报:信息科学版,2003,28(增刊): 32-37.) |
| [5] | CHEN Jun.Dynamic Spatial Data Model Based on Voronoi[M].Beijing:Surveying and Mapping Press, 2002.(陈军.Voronoi动态空间数据模型[M].北京:测绘出版社,2002.) |
| [6] | OKABE A, BOOTS B, SUGIHARA K,et al. Spatial Tessellations Concepts and Applications of Voronoi Diagrams[M]. Chichester:Wiley,2000. |
| [7] | ZHAO Xuesheng, CHEN Jun,WANG Jinzhuang O_QTM-based Algorithm for the Generating of Voronoi Diagram for Spherical Objects[J]. Acta Geodaetica et Cartographica Sinica,2002,31(2):158-163.(赵学胜,陈军,王金庄. 基于O_QTM 的球面Voronoi图的生成算法[J].测绘学报,2002,31(2):158-163.) |
| [8] | XU Xueqiang, ZHOU Yixing, NING Yuemin. Urban Geography[M]. Beijing: Higher Education Press, 1997.(许学强,周一星,宁越敏.城市地理学[M].北京:高等教育出版社,1997.) |
| [9] | WANG Xinsheng, GUO Qingsheng, JIANG Youhua. A New Approach to Delimitate Influenced Coverage of an Economic Object-Voronoi Diagram[J].Geographical Research,2000,19(3):311- 315.(王新生,郭庆胜,姜友华.一种用于界定经济客体空间影响范围的方法-Voronoi 图[J].地理研究,2000,19(3):311-315.) |
| [10] | OKABE A,SATOH T,FURUTA T,et al. Generalized Network Voronoi Diagrams: Concepts,Computational Methods and Applications[J]. International Journal of Geographical Information Science, 2008,22(9):965-994. |
| [11] | XIE Shunping,FENG Xuezhi,LU Wei.Algorithm for Constructing Voronoi Area Diagram Based on Road Network Analysis[J]. Acta Geodaetica et Cartographica Sinica,2010,39(1):88-94.(谢顺平,冯学智,鲁伟.基于道路网络分析的Voronoi面域图构建算法[J].测绘学报,2010,39(1):88-94.) |
| [12] | MILLER H J. Market Area Delimitation within Networks Using Geographic Information Systems[J].Geographical Systems,1994,44(1):157-173. |
| [13] | FURUTA T, SUZUKI A,INAKAWA K. The Kth Nearest Network Voronoi Diagram and Its Application to Districting Problem of Ambulance Systems[R]. Aichi: Nanzan University,2005. |
| [14] | OKABE A, OKUNUKI K. A Computational Method for Estimating the Demand of Retail Stores on a Street Network and Its Implementation in GIS[J]. Transactions in GIS,2001,5(3):209-220. |
| [15] | WANG Xinsheng,YU Ruilin,JIANG Youhua.Delimitating the Store Market Field Based on the Metric of the City-block Distance[J].Geographical Research,2008,27(1):85-92.(王新生,余瑞林,姜友华. 基于道路网络的商业网点市场域分析[J].地理研究,2008,27(1):85-92.) |
| [16] | XIE Shunping,FENG Xuezhi,DU Jinkang.Maximal Covering Spatial Optimization Based on Network Voronoi Diagrams Heuristic and Swarm Intelligence[J]. Acta Geodaetica et Cartographica Sinica,2011,40(6):778-784.(谢顺平,冯学智,都金康. 基于网络Voronoi图启发式和群智能的最大覆盖空间优化[J].测绘学报,2011,40(6):778-784.) |
| [17] | CHEN J. A Raster-based Method for Computing Voronoi Diagrams of Spatial Objects Using Dynamic Distance Transformation[J]. International Journal of Geographical Information Science,1999,13(3):209-225. |
| [18] | ZHAO Renliang, LI Zhilin, CHEN Jun, et al.A Hierachical Raster Method for Computing Voronoi Diagrams Based on Quadtrees[C]//Lecture Notes in Computer Science-Computational Science-ICCS.Amsterdam:Springer,2002: 85-92. |
| [19] | LI Xia,YE Jiaan. Constrained Cellular Automata for Modelling Sustainable Urban Forms[J].Acta Geographica Sinica,1999,54(4):289-298.(黎夏,叶嘉安. 约束性单元自动演化CA模型及可持续城市发展形态的模拟[J].地理学报,1999,54(4):289-298.) |
| [20] | TAN Yili, ZHAO Ye, WANG Yourong. Power Network Voronoi Diagram and Dynamic Construction[J].Journal of Networks, 2012,7( 4):675-682. |