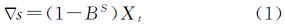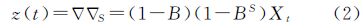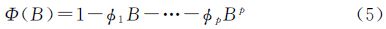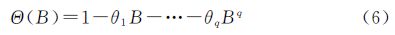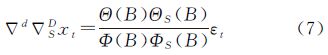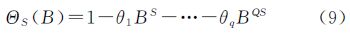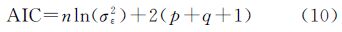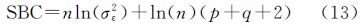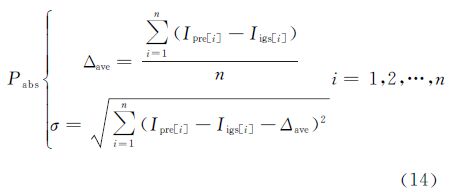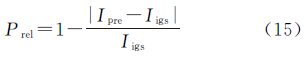1 引 言
电离层与人类生活息息相关,其变化对定位导航、远程通信、航空航天、天气预报等具有重要影响[1, 2, 3, 4]。电离层的时空分布及变化与地球运动、太阳活动、地磁场变化等诸多因素密切相关,观测并预报电离层中的总电子含量(TEC)及其时空分布已成为电离层研究中的一个重要课题,在单频GPS实时导航定位、震前电离层扰动探测等研究中具有重要应用。目前常用的电离层模型Klobuchar、Bent、IRI等经验模型因使用方便且计算简单而被广泛应用,但这些模型都是基于统计经验,对电离层预报结果并不十分理想。常用单频接收机采用的Klobuchar模型在一天内只能预报出电子含量的50%~60%[5],且对夜间的预报具有明显的不合理性;IRI模型的预报精度也只有60%左右,并且由于探测资料在时间分布和地域跨度上的局限,使得结果在不同地区相差较大。因此,国内外学者先后建立了精度较高的电离层预报模型,如神经网络模型、时间序列模型[6, 7, 8, 9, 10, 11, 12, 13, 14, 15]等,并取得了丰富的研究成果。其中,时间序列模型与其他模型相比具有样本数据要求少、建模理论完善、计算过程相对简单、外延性好以及短期电离层预报精度高等优势[12, 13, 14, 15, 16]。自文献[10]提出了以IGS电离层资料为样本利用时间序列方法预报全球电离层TEC以来,虽有少量学者也利用时间序列模型分析预报电离层TEC值并且取得了一定成果,但大多数研究都是基于电离层平静期的TEC值,而对于包含有电离层活跃期TEC值的预报效果却鲜有人提及。此外,已有研究在用时间序列模型分析电离层时,一般都只考虑到残差项中周期性与短期相关性的相加性模型,而忽略了乘积性季节模型的可能性。TEC时间序列在很多情况下都更适合用乘积性季节模型来模拟。
基于此,本文利用CODE提供的高精度电离层TEC资料,采用时间序列模型的分析方法,考虑乘积性季节模型,对不同电离层环境下(电离层平静期和活跃期)和不同纬度地区预报性能和精度,同时重点分析了影响该方法预报精度的因素,如TEC样本数据长度对预报精度的影响以及相同TEC样本数据预测不同天数对预测精度的影响。
2 时间序列法(ARIMA模型)预报电离层TEC电离层TEC的变化与地理位置、季节、地方时以及太阳和地球的活动有密切关系。因此,其TEC值具有明显的年周期变化、季周期变化、日周期变化和随机波动。而时间序列分析可以对一组有序数据进行观察、研究,找到它的变化发展规律,能够较好地预测其走势。
利用时间序列法预报电离层TEC值的基本流程是先获得由CODE提供的TEC值作为样本序列,然后判断序列的平稳性,如果序列不平稳则先进行平稳化处理;得到平稳序列后通过自相关函数和偏自相关函数表现的性质选定模型并定好阶以完成建模过程;建模完成后进行显著性检验,看所选模型是否显著有效;最后,在所有通过检验的模型中按照一定准则选择相对最优模型,进行序列的预测。根据TEC值序列明显的周期性,对TEC序列进行以步长为周期长度S的差分运算,根据观测时序图、观测序列的自相关函数等来判别其周期S,按式(1)进行季节差分
式中,B为后移算子,Xt-s=BsX;▽为差分算子。如差分后的时间序列仍有趋势,则再对季节差分后的时间序列值进行正常差分▽▽s,变为序列z(t)一般情况下,经一次季节差分和一次正常差分后,原序列观测值能够转化为平稳时间序列z(t)。若不能,则继续差分直到平稳。对差分平稳序列可用ARIMA(求和自回归移动平均)模型进行拟合[12]。ARIMA模型又可分为ARIMA(p,d,q)模型和ARIMA(p,d,q)×(P,D,Q)S乘积季节模型。普通ARIMA(p,d,q)模型可表示为式(3)—式(6)
式中,xt为零均值平稳序列;▽d表示d阶差分;εt表示零均值白噪声序列;Φ(B)为平稳可逆ARMA(p,q)模型的自回归系数多项式;Θ(B)为平稳可逆ARMA(p,q)模型的移动平滑系数多项式;非负整数p称为自回归阶数,非负整数q称为滑动平均阶数;实参Φ1、Φ2、…、Φp称为自回归系数,实参θ1、θ2、…、θq称为滑动平均系数[18, 19, 20]。通常情况下,普通的ARIMA模型已经能够模拟出比较准确的模型,但还是有部分序列不能理想模拟。对于有短期相关性和季节效应之间具有复杂关联性的情况,短期相关性和季节效应不能简单地、可加性地提取,此时须用乘积季节模型。其季节相关性可采用以周期步长为单位的ARIMA(p,d,q)模型提取,这样的序列则适合采用ARIMA(p,d,q)×(P,D,Q)S乘积季节模型进行拟合,其完整表达如式(7)—式(9)
式中,▽SD表示D阶以周期S为步长的季节差分运算;S为季节性周期;ΦS(B)为季节性自回归算子,P为季节性自回归阶数,Φ1、Φ2、…、Φp为季节性自回归部分参数;ΘS(B)为季节性移动平均算子,Q为季节性移动平均阶数,θ1、θ2、…、θq为季节性移动平均部分参数[18, 19, 20]。在分析过程中,应根据TEC值的时间序列具体表现出来的性质挑选模型,然后进行模型的检核,反复尝试,直到找出最佳模型。通常情况下,同一个时间序列可以构造多个显著有效的拟合模型。为了解决这个问题,引入AIC准则和SBC准则作为判断标准选择相对最优模型,即在通过检验的模型中使得AIC或SBC函数值达到最小的模型。
AIC准则是拟合精度和参数个数的加权函数。其中,中心化ARMA(p,q)模型的AIC函数为
非中心化ARMA(p,q)模型的AIC函数为SBC是AIC的改进,理论已经证明,SBC准则是最优模型的真实阶数的相合估计[14, 15]。中心化ARMA(p,q)模型的SBC函数为
非中心化ARMA(p,q)模型的SBC函数为
3 试验分析本文利用CODE提供的高精度全球电离层TEC数据作为样本序列,选取电离层平静期、活跃期不同地理纬度的TEC数据采用ARIMA模型进行短期预报,其预报结果与CODE所提供TEC值(作为真实值)进行比较,得到预报精度。为了考察预报结果的精度,笔者采用相对精度Prel和绝对精度Pabs{Iave,σ}
式中,Δave为预报值与真值的平均残差;σ为预报残差的中误差;Ipre为预报的电离层TEC值;Iigs为IGS发布的TEC值;n为预报的数据量。 3.1 不同环境下的预报精度分析在利用时间序列分析进行电离层TEC预测时,对于包含电离层处于活跃时期数据的预报结果鲜有人提及,因此笔者对电离层活跃程度如何影响预报结果进行了分析探讨,得出一些具有参考价值的结果。
对电离层活跃期的预报分析,笔者选取2010年年积日为47—60日(2010-02-16—2010-03-01)、227—240日(2010-08-15—2010-08-25)两个时段内高纬度(70°N,115°E)、中纬度(40°N,115°E)和低纬度(10°N,115°E)电离层格网TEC数据;对电离层平静期的电离层预报分析,笔者选取2012-03-06—2012-03-14、2011-09-09—2011-09-22、2010-08-01—2010-08-14、2008-02-01—2008-02-14这4个时段IGS提供的高纬度(75°N,125°E)、中纬度(45°N,125°E)和低纬度(5°N,125°E)的格网TEC数据,4段数据包含了春夏秋冬的情况,且电离层活跃期持续较长。然后,用前8 d的TEC值预报后6 d的TEC值,并与发布的真实值作比较,其结果如图 1和图 2所示。
|
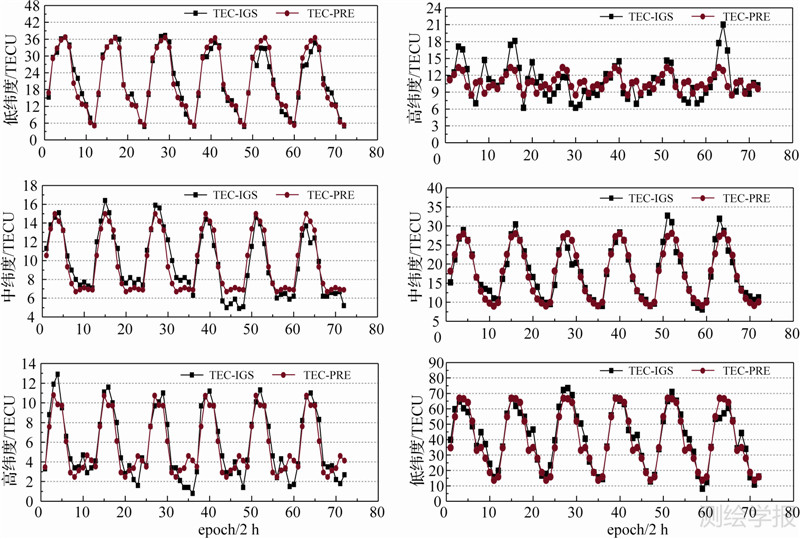
| 图 1 电离层平静期(左图)与活跃期(右图)在不同纬度的TEC预报结果 Fig. 1 TEC forecast result comparison at different latitudes in ionospheric quiet period |
|
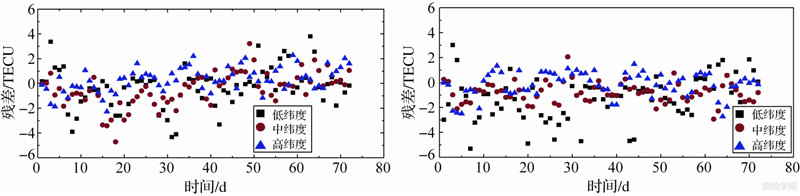
| 图 2 电离层平静期(左图)与活跃期(右图)在不同纬度的预报残差 Fig. 2 Predicted residual value at different latitudes in ionospheric quiet period |
图 1为2010-02-24—2010-03-01不同纬度的预测结果与实际观测结果的对比图,图中横坐标轴表示预测历元,其中每2 h一个历元;纵坐标轴表示TEC值,单位为TECU;红色(TEC-PRE)代表预测值,黑色(TEC-IGS)表示IGS提供的实际观测值。图 2为预测结果与实际观测结果之差的散点图,即残差散点图,其中横坐标轴表示预测历元;纵坐标轴为预测值与真实值之差,单位为TECU。其中,图 2中的蓝色三角形、红色圆形、黑色正方形分别代表高、中、低纬度每个历元的预报残差。
由图 1和图 2可以看出,在电离层平静期与活跃期,利用基于ARIMA模型的时间序列分析法预测得到的TEC值与实际观测值在高、中、低纬度均符合的较好,并且在大多数情况下,预报残差在3 TECU以内,与IGS本身提供TEC值精度相当。且预报残差会随纬度的增加而减小。对比电离层平静期和电离层活跃期,电离层活跃期预报精度要稍差一些,特别是在低纬度地区,其残差值明显要差于平静期。
由表 1的残差统计结果可以看出,电离层平静期的预报结果将近50%的数据预报残差在1 TECU内,90%的预报残差在3 TECU内;而电离层活跃期预报残差小于1 TECU的占44.0%,与电离层平静期相差不大,而预报残差大于3 TECu的则为20%,比平静期的10%大两倍,说明在电离层活跃期由于电离层的不稳定性导致时间序列法对其建模存在一定偏差,从而使得预报结果相对较差。但总体来说,时间序列方法具有较高预报精度,是一种比较理想的预测方法。
| (%) | |||||||||||
| Days | Δ<1 TECU | 1 TECU≤Δ<2 TECU | 2 TECU≤Δ<3 TECU | Δ≥3 TECU | |||||||
| 平静期 | 活跃期 | 平静期 | 活跃期 | 平静期 | 活跃期 | 平静期 | 活跃期 | ||||
| 1 | 61.1 | 39.6 | 23.6 | 20.2 | 7.0 | 13.2 | 8.4 | 27.1 | |||
| 2 | 55.5 | 40.3 | 20.9 | 22.9 | 9.7 | 18.0 | 13.9 | 18.8 | |||
| 3 | 50.0 | 43.1 | 22.2 | 27.1 | 13.9 | 9.0 | 13.9 | 20.8 | |||
| 4 | 43.1 | 47.9 | 36.1 | 30.6 | 15.3 | 6.3 | 5.6 | 15.3 | |||
| 5 | 50.0 | 46.5 | 22.2 | 18.1 | 15.3 | 18.8 | 12.5 | 16.7 | |||
| 6 | 43.0 | 45.9 | 33.3 | 22.2 | 15.3 | 10.4 | 8.4 | 21.5 | |||
| 均值 | 50.0 | 44.0 | 26.0 | 24.0 | 13.0 | 13.0 | 10.0 | 20.0 | |||
由表 2给出的电离层平静期精度统计表可知,不同纬度预报值的相对精度有着较大差异,低纬度最高,中纬度、高纬度次之;而对于绝对精度(即平均残差值和中误差),高纬度地区明显要优于中、低纬度。造成不同纬度相对精度和绝对精度恰好相反是由于在低纬度地区受太阳影响,其本身电离层TEC值较大,从而导致即使预报残差较大,其相对精度也会比较高,而高纬度地区则恰好相反。
| 预报天数 | 低纬度 | 中纬度 | 高纬度 | ||||||||
| Δave | σ | Prel/(%) | Δave | σ | Prel/(%) | Δave | σ | Prel/(%) | |||
| 1 | 0.41 | 2.46 | 89.14 | 0.68 | 0.83 | 91.34 | 0.41 | 1.04 | 86.12 | ||
| 2 | 0.78 | 1.61 | 94.14 | 2.1 | 1.79 | 83.10 | 0.23 | 1.39 | 78.67 | ||
| 3 | 1.22 | 2.15 | 90.39 | 1.07 | 1.19 | 89.47 | -0.69 | 1.23 | 54.27 | ||
| 4 | 0.85 | 1.5 | 89.51 | -0.27 | 1.11 | 86.83 | -0.5 | 1.17 | 73.08 | ||
| 5 | -0.91 | 2.62 | 86.16 | -0.21 | 1.31 | 88.14 | -0.55 | 1.43 | 69.19 | ||
| 6 | -0.26 | 2.5 | 88.71 | -0.53 | 1 | 90.23 | -0.71 | 1.26 | 69.58 | ||
| 均值 | 0.35 | 2.14 | 89.68 | 0.47 | 1.2 | 88.18 | -0.3 | 1.25 | 71.82 | ||
结合表 3电离层活跃期的预报精度统计表,采用包含活跃期的数据作为样本序列来进行预测时,其相对精度比平静期虽然略高,但预报残差要比平静期预报大。这是由于相对精度的计算结果在一定程度取决于基值相的太大,相同或相近的预报残差,若基值不同,相对精度会有较大差异;而活跃期的基值一般都比平静期的基值要大,所以即使残差较大,仍可保持略高的相对精度。由此可以判断,残差项的比较比相对精度的比较更有说服力。因此,可以认为,包含活跃期的数据做样本序列来预报电离层TEC值序列预报精度不如完全采用平静期数据做样本序列进行预报的精度,但差异并不是太大。
| 预报时间 | 低纬度 | 中纬度 | 高纬度 | ||||||||
| Δave | σ | Prel/(%) | Δave | σ | Prel/(%) | Δave | σ | Prel/(%) | |||
| 1 | 1.44 | 3.5 | 89.11 | 0.84 | 1.79 | 87.20 | 0.82 | 1.76 | 80.98 | ||
| 2 | 1.71 | 3 | 89.24 | 0.9 | 1.49 | 88.98 | -0.01 | 1.53 | 78.84 | ||
| 3 | 2.59 | 3.1 | 88.51 | 0.52 | 1.63 | 88.99 | -0.58 | 1.26 | 81.59 | ||
| 4 | 1.62 | 2.49 | 91.11 | 0.62 | 1.15 | 90.88 | 0.15 | 1.53 | 82.37 | ||
| 5 | 1.08 | 2.84 | 88.83 | 1.01 | 1.47 | 88.65 | 0.02 | 1.28 | 85.68 | ||
| 6 | -0.36 | 3.98 | 88.94 | 1.05 | 1.46 | 88.91 | 0.52 | 1.54 | 80.60 | ||
| 均值 | 1.35 | 3.15 | 89.29 | 0.82 | 1.5 | 88.94 | 0.15 | 1.48 | 81.68 | ||
以往研究中虽然介绍了相关基于ARIMA模型的电离层预报方法,但是却没有较为全面的分析预测结果精度的影响因素,使得无法使用最佳的预报方式得到最好预报结果。因此,笔者对影响该方法预报精度的影响因素做了重点分析。其包括两方面:一方面是所采用样本数据的长短对预报结果的影响(即多少天的样本数据才是最佳样本数据),而另一方面,笔者分析了该方法利用同样的样本数据预报数天,分析其最大预测长度。以便后续为运用该方法提供重要参考。
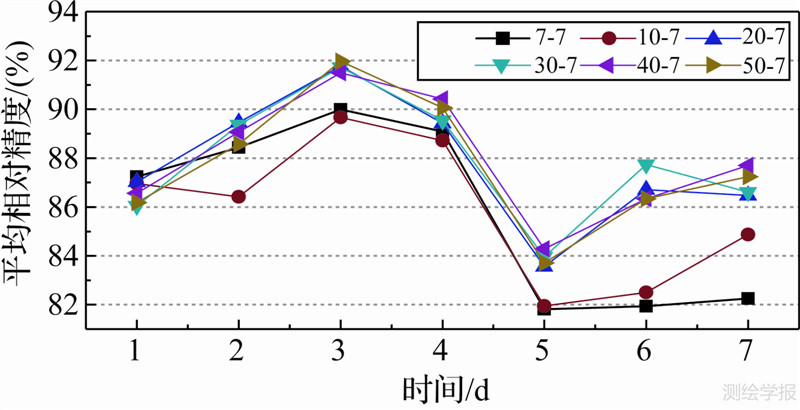
首先,笔者取2009年年积日70—126 CODE提供的高纬度(75°N,125°E)、中纬度(45°N,125°E)和低纬度(5°N,125°E)的格网TEC数据作为序列样本进行时间序列分析,采用7-7(即利用7 d的数据来预测之后7 d的TEC结果)、10-7、20-7、30-7、40-7、50-7 6种模式来研究预报所采用天数对预报结果的影响,图 3给出了6种方式预测的相对精度对比图。
|
| 图 3 6种预测模式的相对精度对比图 Fig. 3 Comparison figure of the six predicting patterns’ relative accuracy |
由图 3可以看出,样本序列的长度对预测精度有一定影响,在最初,样本序列的增长能够很明显地提高预测相对精度;但随着样本继续增长,到一定长度后变化不再明显;超过一定长度后,随着样本序列的增长,预报精度开始下降。由图可以看出,30 d左右为最佳样本序列长度,如果再增加样本长度对相对精度不会有明显的提高。
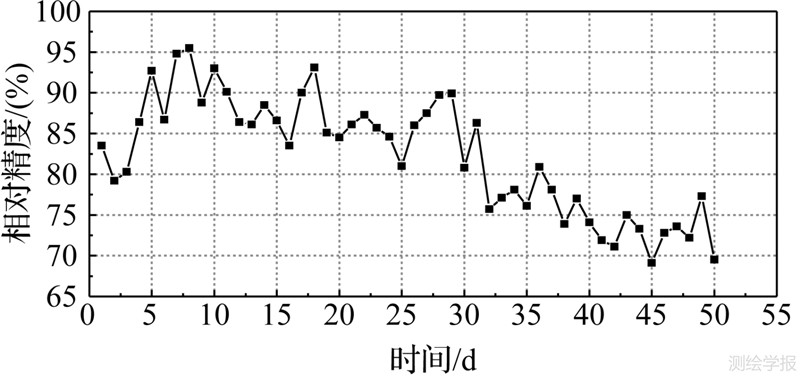
然后,笔者利用2010年年积日为227—240日(10°N,115°E)的TEC样本序列向后预报50 d,分析了该方法预测精度随着预报天数增加的变化规律,图 4给出了预报精度随时间的变化图(给出的为每天12个时段的平均相对精度),其结果如图 4所示,其中横坐标轴表示预报的预报天数;纵坐标轴为预报的相对精度。
|
| 图 4 预报50 d每天的平均相对精度统计图 Fig. 4 Everyday’s average relative accuracy statistical figure of predictions in 50 days |
由图 4可以看出,随着预报时间的增加,预报精度大致呈现下降的趋势。但是预测长度在前30 d左右平均相对精度差不多都在80%以上,且在前10 d平均相对精度在90%左右,而超过30 d预报的相对精度明显下降,随时间增加相对精度衰减越快。预报初期之所以出现精度逐渐增加的现象,跟其电离层异常有一定关系,导致预报初期的3~5 d精度较低,而后来逐渐恢复正常。
4 结 论基于ARIMA模型的方法是基于数学方法的预报,使用较简单且预测结果较为理想,以分析该方法在不同电离层状况下的预测性能和影响该方法精度的因素分析。经大量试验,分析得到如下结论:
(1) 该方法在预报电离层TEC中是可行的而且有较大的应用价值。其预测的平均相对精度可达83%;而平均绝对精度(即残差)为0.18 TECU,其中残差值小于3 TECU的占到90%以上。
(2) 无论是在电离层活跃期还是平静期,该方法均能得到较好的预测结果。两者预报的相对精度基本相当,而电离层活跃期相对于平静期的预报绝对精度要稍差,但也属于较为理想的精度范围。
(3) 该方法预测时所采用的样本数据长度和预报时间长度,都会造成预报精度的差异。其规律是:预报所采用的天数(即TEC样本数据长短)对结果有较明显的影响。在一定范围内,当预报所采用的天数较多时,结果的可靠性也就较强,达到的精度更高;但随着样本序列增加到一定值(约30 d左右)后,其相对精度提高不大。而同样的TEC样本数据,一般预测时间越长精度越低,而前30 d其精度波动幅度不大,但是超过30 d,则精度会随时间出现明显的衰减。
| [1] | CAI Changsheng, GAO Jingxiang, LI Zhenghang. Monitoring Seasonal Variations of Ionospheric TEC Using GPS Measurements [J]. Geomatics and Information Science of Wuhan University, 2006,31(5):451-453.(蔡昌盛, 高井祥, 李征航. 利用GPS监测电离层总电子含量的季节性变化[J]. 武汉大学学报: 信息科学版, 2006, 31(5):451-453.) |
| [2] | YUAN Yunbin. Study on Theories and Methods of Correcting Ionospheric Delay and Monitoring Ionosphere Based on GPS[D] . Wuhan: Institute of Geodesy and Geophysics of the Chinese Academy of Sciences , 2002.( 袁运斌. 基于GPS的电离层监测及延迟改正理论与方法的研究[D]. 武汉:中国科学院测量与地球物理研究所,2002.) |
| [3] | MENG Yang ,AN Jiachun, WANG Zemin, et al. Spatial Distribution of Antarctic Ionosphere TEC Based on GPS[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1): 37-40.(孟泱, 安家春, 王泽民, 等. 基于 GPS 的南极电离层电子总含量空间分布特征研究[J]. 测绘学报, 2011, 40(1):37-40.) |
| [4] | BHUYAN P K, BORAH R R . TEC Derived from GPS Network in India and Comparison with the IRI [J].Advances in Space Research, 2007, 39(5):830-840. |
| [5] | RUAN Rengui, WU Xianping, FENG Laiping,et al. Single-Frequency Precise Point Positioning with Simultaneous Ionospheric Delay Estimation[J]. Acta Geodaetica et Cartographica Sinica,2012,41(4):490-495.(阮仁桂, 吴显平,冯来平,等.同时估计电离层延迟的单频精密单点定位方法[J]. 测绘学报, 2012,41(4): 490-495.) |
| [6] | FAN Guoqing , WANG Wei, XI Xiaoning . Modeling of Ionosphere VTEC Using Generalized Regression Neural Network[J]. Acta Geodaetica et Cartographica Sinica, 2010,39(1):16-21. (范国清, 王威, 郗晓宁. 基于广义回归神经网络的电离层VTEC建模[J]. 测绘学报, 2010, 39(1):16-21.) |
| [7] | RATNAM V D, DINESH V B, TEJASWI B, et al. TEC Prediction Model Using Neural Networks over a Low Latitude GPS Station[J].International Journal of Soft Computing and Engineering, 2012, 2 (2) :2231-2307. |
| [8] | HABARULEMA J B. A Feasibility Study into Total Electron Content Prediction Using Neural Networks[D]. Grahamstown: Rhodes University, 2008. |
| [9] | HABARULEMA J B, MCKINNELL L A, CILLIERS P J. Prediction of Global Positioning System Total Electron Content Using Neural Networks over South Africa[J]. Journal of Atmospheric and Solar-terrestrial Physics, 2007,69(15):1842-1850. |
| [10] | LIU Xiandong,SONG Lijie,YANG Xiaohui,et al. Predicting Shortdated Ionospheric TEC Based on Wavelet Neural Network[J]. Hydrographic Surveying and Charting, 2010,30(5):49-51.(刘先冬, 宋力杰, 杨晓晖. 基于小波神经网络的电离层 TEC 短期预报[J]. 海洋测绘, 2010, 30(5):49-51.) |
| [11] | AKYILMAZ O, ARSLAN N. An Experiment of Predicting Total Electron Content(TEC) by Fuzzy Inference Systems[J]. Earth, Planets, and Space, 2008, 60(9):967-972. |
| [12] | LI Zhigang, CHENG Zongyi, FENG Chugang, et al. A Study of Prediction Models for Ionosphere[J]. Chinese Journal of Geophysics, 2007, 50( 2) :327-337.(李志刚, 程宗颐, 冯初刚, 等. 电离层预报模型研究[J]. 地球物理学报, 2007, 50 (2):327-337.) |
| [13] | ERDOGAN H, ARSLAN N. Identification of Vertical Total Electron Content by Time Series Analysis[J]. Digital Signal Processing, 2009, 19(4):740-749. |
| [14] | LI Xiuhai, GUO Dazhi. Prediction of Ionospheric Total Electron Content Based on Semiparametric Autoregressive Model[J]. Science of Surveying and Mapping, 2011(2):149-151.(李秀海, 郭达志. 基于半参数AR 模型的电离层TEC 建模与预测[J]. 测绘科学, 2011(2):149-151.) |
| [15] | LI Xiuhai, GUO Dazhi.Modeling and Prediction of Ionospheric Total Electron Content by Time Series Analysis[C]//International Conference on Advanced Computer Control. Shenyang: [s.n.], 2010: 375-379. |
| [16] | LI S H,PENG J H. Time Series Analysis and Prediction on Ionospheric VTEC Data[C]//CPGPS 2009:Proceedings of Global Navigation Satellite System:Technology Innovation and Application,2009:155-161. |
| [17] | KRANKOWSKI A.Wavelet Analysis and Forecasting of VTEC Obtained with GPS Observations over European Latitudes[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2005. 67(12):1147-1156. |
| [18] | JAMES D H. Time Series Analysis[M].New Jersey:Princeton University Press,1994. |
| [19] | WANG Yan. Application of Time Series Analysis[M]. 2nd. Beijing: People's University of China Press, 2008.(王燕. 应用时间序列分析[M]. 2版. 北京: 中国人民大学出版社, 2008.) |
| [20] | HE Shuyuan. Application of Time Series Analysis[M]. Beijing: Beijing University Press, 2007.(何书元. 应用时间序列分析[M]. 北京: 北京大学出版社,2007.) |