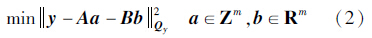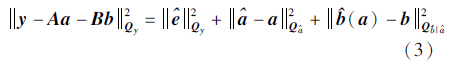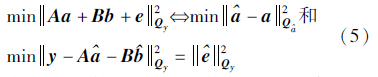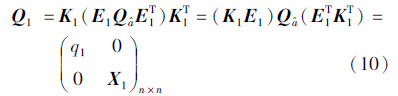2. 武汉大学 测绘学院,湖北 武汉 430079;
3. Space Research Centre, RMIT University, Melbourne 3001 VIC, Australia
2.School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
3. Space Research Centre, RMIT University, Melbourne 3001 VIC, Australia
1 前言
相位整数模糊度的快速、精确解算是GNSS实时高精度动态定位的关键问题,也是GNSS研究领域中多年来的热点问题。国内外众多学者均对此问题做过了深入研究,先后提出了不同的模糊度解算方法,如模糊度函数法[1],最小二乘搜索法[2]以及FARA法[3],FASF法[4],这些方法都是直接采用搜索的技术获得模糊度的最优整数向量,由于模糊度之间存在相关性,使得上述方法搜索效率较低。文献[5]提出LAMBDA方法用于解算整数模糊度,极大地提高了模糊度的搜索效率。其基本思想是首先基于整数Lagrange降相关原理,通过整数变换方法降低模糊度之间的相关性,然后在整数变换后的空间内,再采用搜索的技术获得其最优模糊度向量,从而极大地提高了模糊度的解算效率。随后许多学者提出了不同的模糊度降相关方法,如文献[6]和文献[7]分别提出利用混合上三角与下三角整数LDLT分解方法。文献[8]提出了统一降相关方法,其采用LDLT分解方法混合完全旋转排序策略,以获得较好的降相关性能。文献[9]提出逆整数LDLT分解的整数降相关,降相关后可获得更小的条件数。文献[10]提出了完全旋转排序、贪婪选择等策略,以改进LAMBDA中的降相关方法,进一步提高了该降相关方法的计算效率。文献[11]提出混合(逆)上三角与(逆)下三角的整数LDLT分解方法,以提高高维模糊度的降相关的性能。文献[12]提出基于并行排序的整数LDLT分解方法,文中指出采用并行排序的算法可以获得更低的条件数,同时文中详细介绍了整数最小二乘解算问题的研究发展历程。文献[13]指出条件数并不能用作降相关的性能评价指标,在此基础上,提出了部分降相关算法,有效地提高了降相关的效率。上述降相关方法都是基于LDLT分解,降相关的条件都类似,即要求将降相关后的模糊度方差协方差阵接近对角矩阵,且D矩阵的对角线元素为降序或升序排列。其中LAMBDA方法中的多维Lagrange整数降相关利用两个相邻列向量之间的距离约束达到降相关目的,统一降相关利用列LDLT混合完全旋转排序策略实现对多个列向量的距离约束,基于并行排序的LDLT分解方法综合利用不同的排序方法,期望实现更好的约束条件。不同的排序方法可以获得不同降相关性能,最终影响模糊度的搜索效率,但是目前只是从降相关后矩阵的条件数来确定降相关的性能,而没有从理论上证明排序对降相关性能的影响[14]。
GNSS整数模糊度解算问题实际上是个格上的著名难题——最近向量问题。格上问题的研究起源于Lagrange[15],Lagrange 在研究二次齐式的规约中,最早提出了二维整数规约方法。在数的几何学中,该方法被称为格基规约(Lattice Reduction)。通过Lagrange规约,可以在多项式时间(在计算复杂度理论中,多项式时间指的是一个问题的计算时间不大于问题大小的多项式倍数)内找到一个二维格中的最短向量。Gauss 引用该方法解决类似的问题[16],随后在多个领域中,都称该方法为二维Gauss规约,在本文中仍称之为Lagrange规约。Hermite提出任意维数格基的规约条件,称之为Hermite 规约[17];Korkine 和 Zolotareff 加强了Hermite规约条件,被称为HKZ规约[18];Minkowski提出新的任意维格基的规约条件,称之为Minkowski规约[19]。关于格上问题的早期研究历程,读者可参考文献[20]。上述研究偏重于理论,此后相关学者设计了满足对应规约条件的格基规约算法:如Kannan提出的Kannan算法,其规约基满足HKZ规约条件[21];Bettina提出满足Minkowski 规约条件的算法[22]。然而对于高维的格基,上述算法并不能在多项式时间内找到满足对应规约条件的格基[23]。文献[24]通过弱化HKZ规约条件,提出了LLL规约条件,并设计了对应的算法,使用该算法可以在多项式时间内找到一个n维格中的短向量,该短向量的长度不超过格中最短向量长度的2(n-1)/2倍。文献[25]提出了BKZ规约条件,并设计了BKZ算法,该算法可以在计算复杂度和规约条件之间做折中处理,其最强规约基满足HKZ规约条件,最弱规约基满足LLL规约条件。
格基规约方法在多个领域中都得到广泛的应用,如通信、密码学等[26]。文献[27]最早提出采用LLL格基规约算法用于辅助GPS模糊度解算,并指出LAMBDA方法中的降相关方法等价于LLL格基规约算法;文献[28]介绍了LLL格基规约算法用于辅助GPS模糊度解算的流程,并提供该算法的源代码。文献[14]引入了基于格论的模糊度解算方法,并针对未来多频多系统GNSS导航定位的需要,系统比较分析了不同基线长度情况下,格基规约方法的性能。文献[29]理论证明了LLL格基规约可有效提高模糊度的搜索效率。
目前存在有多种降相关方法或格基规约方法,由于LLL规约算法的计算复杂度为多项式时间,从而得到广泛的应用。但是对于GNSS模糊度解算而言,目前仍然存在不少问题,如对于未来的多频GNSS精密实时定位,尤其是长基线相对定位或精密单点定位,其模糊度维数较高,而且由于电离层、对流层误差等影响,模糊度之间会存在有很强的相关性。此时不仅需要较长的模糊度搜索时间,而且缺少可靠的模糊度检验指标。虽然LLL格基规约可以减少模糊度的搜索时间,也可以提高模糊度解算的Bootstrapping 成功率[30],为高维模糊度解算提供可靠的检验指标。但是由于其弱化的规约条件,只能在一定程度上减少模糊度的搜索时间和提高Bootstrapping 成功率。因此为了实现多频GNSS实时模糊度准确解算,有必要研究性能更好的规约条件及其算法,既算法本身耗时较少,同时又能提高模糊的搜索效率及其可靠性检验指标(Bootstrapping 成功率)。
基于此,本文在介绍格论的基本理论基础上,将目前GNSS领域中降相关方法统一至格论框架下,并建议采用Bootstrapping成功率作为格基规约的性能指标之一,接着从理论上论证不同降相关方法的规约强度,最后通过仿真的多频GNSS数据,分析高维情况下,不同降相关方法获得的Bootstrapping成功率。
2 GNSS相对定位数学模型GNSS观测方程为[30]
式中,a为载波相位模糊度参数;b为基线分量、对流层、电离层等待估参数;e为观测噪声;y为载波相位与伪距观测值;A、B为设计矩阵;Qy为y观测值的方差协方差阵。
当考虑模糊度参数为整数时,上式可进一步正交分解为
式中
式中,
 为模糊度的实数值;
为模糊度的实数值; 为模糊度实数解对应的基线;
为模糊度实数解对应的基线; (a)为模糊度固定解对应的基线分量。
(a)为模糊度固定解对应的基线分量。
由于式(1)中的b是实数值的,故式(3)右边第3项应为零,当考虑整数约束时,式(3)最优估计准则等价于其右边两项的最优估计问题
式(5)中a为整数矢量,由于模糊度之间存在相关性,通常采用搜索的方法获得最优整数矢量值,但是当模糊度维数较高或精度较低时,此时搜索算法会耗费较多的时间。为了快速获得模糊度的整数值,通常采用降相关处理,降低模糊度间的相关性,从而减少模糊度的搜索空间。目前GNSS领域中有3种常用的模糊度降相关方法,LAMBDA方法中的多维Lagrange整数变换[30],以及统一降相关[8],并行排序整数LDLT分解[12],3种方法都是基于LDLT分解。
对原始的模糊度方差协方差矩阵 进行LDLT分解并乘以整数变换矩阵得
进行LDLT分解并乘以整数变换矩阵得
式中,Z是整数幺模矩阵。当L为下三角矩阵时,降相关方法要求转换后的方差协方差矩阵
 具有两个条件[30]:
具有两个条件[30]:
(1)  尽可能地对角化;
尽可能地对角化;
(2) 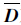 对角线元素按递增顺序排列
对角线元素按递增顺序排列 。
。
即对应于以下条件[28]
统一降相关与并行排序整数LDLT分解的方法要求 矩阵的对角线元素满足一定的排序,统一降相关基于完全旋转(complete pivoting)策略获得更好排序,并行排序整数LDLT分解采用混合上升排序与完全旋转策略排序。
矩阵的对角线元素满足一定的排序,统一降相关基于完全旋转(complete pivoting)策略获得更好排序,并行排序整数LDLT分解采用混合上升排序与完全旋转策略排序。
式中 式中,ls1为矩阵
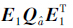 中的第1列第s行元素; E1为旋转矩阵,可使得矩阵
中的第1列第s行元素; E1为旋转矩阵,可使得矩阵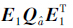 中的第1行、第1列元素为
中的第1行、第1列元素为 中的最小元素q1。经过K1分解后获得Q1,其子块X1为对称正定矩阵,继续采用上述方法获得子块X1最小元素,直到最后一列。
中的最小元素q1。经过K1分解后获得Q1,其子块X1为对称正定矩阵,继续采用上述方法获得子块X1最小元素,直到最后一列。
目前GNSS领域中的模糊度降相关方法都是基于整数LDLT分解,并结合不同的排序方法,不同排序方法可以获得不同降相关性能,最终影响模糊度的搜索效率。但是目前只是从降相关后矩阵的条件数来确定降相关的性能,没有从理论上证明排序对降相关性能的影响。本文从格论出发,理论论证完全旋转策略排序方法的降相关性能,及其对模糊度解算的影响。
3 格的基本定义与定理格的定义来源于数的几何学[32],格上计算存在两个著名的难题,分别是最短向量问题与最近向量问题,GNSS模糊度解算对应于格上的最近向量问题。以下简要介绍格的定义。
3.1 格的定义[32]定义1:设向量b1,b2,…,bn∈Rm线性无关,由向量b1,b2,…,bn生成的格(Lattice)定义为
式中,B为向量b1、b2、…、bn组成m×n矩阵,称b1、b2、…、bn为格L(B)的一组基。格L(B)的秩为n,维数为m,当n=m时,则称格L(B)是满秩的。在GNSS模糊度解算中,由于实数模糊度与解算的整数模糊度的个数相同,此时格是满秩的。对于非满秩格的格基规约方法,可参考文献[33]。
定义2:设方阵U∈Zn×n,如果 =1,则称U是幺模矩阵。此矩阵对应于GNSS模糊度降相关方法中的幺模矩阵[31]。
=1,则称U是幺模矩阵。此矩阵对应于GNSS模糊度降相关方法中的幺模矩阵[31]。
定义3:格L(B)的基向量B张成的实空间定义为格的跨度(span):
3.2 LLL格基规约
定义1 :设b1,b2,…,bn∈Rn是一组基,如果满足[24]
则称这组有序的基b1,b2,…,bn是以参数δ规约的LLL规约基(LLL reduced basis),其中b*k是对应的Gram-Schmidt正交基。式(14)表示任意两个基向量bk、bj之间的要接近正交;式(15)是对相邻格基向量的长度约束,当δ取值为1,此时约束最强。设πk(bk)为基向量bk在子格L(b1,…,bk-1)跨度的正交补空间上的投影,即bk对应的Gram-Schmidt正交基。当δ=1时,式(15)可表示为[26]
式中,πk-1(bk)是对应于bk在子格L(b1,…,bk-2)跨度的正交补空间上的投影。 4 基于格论的GNSS模糊度解算
令H为式(5)中模糊度方差协方差阵 的Cholesky分解下三角矩阵H
的Cholesky分解下三角矩阵H
则式(5)可表示为
则基于格论的GNSS模糊度解算方程可表示为
式中,T=H-1。由于矩阵T是满秩方阵,因此T的列向量t1,t2,…,tn线性无关,其对应的格为Λ={Ta|a∈Zn},因此GNSS模糊度解算对应于格上的最近向量问题,即在格Λ找一个向量Ta,使得其与向量
 的距离最近。利用格基规约方法对T矩阵进行规约,以获得接近正交的基,从而加快模糊度的搜索[29]。
5 模糊度降相关与格基规约的等价性
的距离最近。利用格基规约方法对T矩阵进行规约,以获得接近正交的基,从而加快模糊度的搜索[29]。
5 模糊度降相关与格基规约的等价性
模糊度降相关的方法(正定二次型消减)等价于格基规约[12, 26],但是存在有不同的模糊度降相关方法,不同方法的降相关性能指标只是采用降相关后的条件数做统计分析,并没有理论证明不同降相关方法的性能指标,下文将降相关方法统一至格理论框架下,从而理论证明不同降相关方法的性能。
对式(17)的H矩阵进行Gram-Schmidt正交化
把上式代入式(17)可得
由式(21)可知,LLL规约基的Gram-Schmidt正交基的内积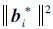 对应于LDLT分解中D的对角线元素,当LLL规约基参数δ=1时,式(9)与式(15)是等价的。
对应于LDLT分解中D的对角线元素,当LLL规约基参数δ=1时,式(9)与式(15)是等价的。
由式(10)可得
式中,q1对应于
 中的最小对角线元素,且q1=
中的最小对角线元素,且q1= ,满足
,满足 ,
, ,继续对X1采用相似的处理,可得q2=
,继续对X1采用相似的处理,可得q2= ,满足
,满足 =min
=min ,…,
,…, ,以此类推,可知完全旋转策略排序的整数LDLT分解服从下面规约条件。
,以此类推,可知完全旋转策略排序的整数LDLT分解服从下面规约条件。
由于D的行列式为常量,由算术-几何平均不等式可知,当D的对角线元素完全相同时,它们的算术平均值最小,此时格基规约性能最强,即式(15)中δ-μ2k,k-1=1。但是由于幺模矩阵的属性限制,此规约基并不一定存在。文献[34]给出LLL规约,LLL-Deep规约,BKZ规约(k=24),HKZ规约的δ-μ2k,k-1均值分别为0.925 9,0.952 4,0.967 1,0.967 1,式(24)同样为LLL-Deep规约条件[35]。比较式(16)与式(24),可知,LLL格基规约仅对相邻的两个基向量进行长度约束,寻找投影距离最小的向量,而完全旋转策略排序的整数LDLT分解是对当前向量及其后所有向量投影距离进行比较,寻找投影距离最小的向量,其规约条件比 LLL格基规约更强。
文献[27, 28]在基于LLL格基规约辅助载波相位模糊度解算时,都是对式(19)中的格L(T)直接进行格基规约,对应于对模糊度的权阵( 的逆矩阵)进行降相关。而文献[30]是对模糊度方差协方差矩阵
的逆矩阵)进行降相关。而文献[30]是对模糊度方差协方差矩阵 进行降相关,即等价于采用LLL格基规约对式(17)的格L(H)进行规约。在格论中,格L(T)称为格L(H)的对偶格[26],当对格L(T)规约时,其对偶格L(H)同时被规约。文献[36]提出对格及其对偶格同时规约的算法,可获得更加正交的规约基。文献[37]采用HKZ算法分别对格及其对偶格进行规约,以获得其中最好的规约基。针对GNSS模糊度解算而言,我们建议对格L(H)(对应于模糊度方差协方差阵)进行规约,其主要原因是只有当模糊度精度较高时,即矩阵
进行降相关,即等价于采用LLL格基规约对式(17)的格L(H)进行规约。在格论中,格L(T)称为格L(H)的对偶格[26],当对格L(T)规约时,其对偶格L(H)同时被规约。文献[36]提出对格及其对偶格同时规约的算法,可获得更加正交的规约基。文献[37]采用HKZ算法分别对格及其对偶格进行规约,以获得其中最好的规约基。针对GNSS模糊度解算而言,我们建议对格L(H)(对应于模糊度方差协方差阵)进行规约,其主要原因是只有当模糊度精度较高时,即矩阵 中元素较小时,解算的整数模糊度才有较高的可靠性,此时对格L(H)规约可以获得比对偶格L(T)规约更好的规约基。
中元素较小时,解算的整数模糊度才有较高的可靠性,此时对格L(H)规约可以获得比对偶格L(T)规约更好的规约基。
降相关或格基规约方法虽然可以提高模糊度的搜索效率,但是不同降相关方法或格基规约方法对模糊度搜索效率的影响,目前还没有统一的结论。降相关方法采用矩阵降相关后的条件数作为其性能指标,而格基规约方法采用规约基最短向量的长度作为其规约强度指标。上述指标高,并不代表对应的模糊度搜索效率就会一定提高。为了获得可靠的性能指标,文中基于搜索算法本身的特点以及结合GNSS模糊度解算的需要,建议采用Bootstrapping成功率作为降相关的性能指标之一。
GNSS模糊度解算中存在有3类常用的估计方法:直接取整估计,Bootstrap估计,以及整数最小二乘估计。它们是基于统计学原理,更关注参数的统计性质。这3类估计分别对应于格论领域中的Rounding off算法,最近平面算法[38] 与最近向量搜索算法[39],在格论中更关注算法本身的计算复杂度问题。3类估计在格上的Voronoi 区域如图 1所示[35, 40],其中六边形(红色)对应于整数最小二乘估计的Voronoi 区域,矩形(蓝色)对应于Bootstrap估计的Voronoi 区域,平行四边形(黑色)对应于直接取整估计的Voronoi 区域。向量(b1,b2)服从二维标准正态分布,概率密度在Voronoi 区域内的积分即为该估计的成功率。3类估计中,直接取整估计解算成功率最低,Bootstrapping成功率低于或等于整数最小二乘估计的成功率。其中Bootstrapping成功率计算相对简单,而整数最小二乘估计的成功率难以直接计算,通常采用Bootstrapping成功率作为其下边界[41, 42]。但是对于多频GNSS长基线相对定位时,由于模糊度维数较高,且模糊度之间具有较强的相关性时,Bootstrapping成功率与整数最小二乘估计的成功率之间将会存在较大差值(见试验分析部分)。此时以Bootstrapping成功率作为整数最小二乘估计的成功率的低边将会过于保守,因此对于实时的多频GNSS长基线相对定位,有必要减少Bootstrapping成功率与整数最小二乘估计的成功率的差值,提高实时模糊度解算的可靠性。

|
| 图 1 3类模糊度估计的Voronoi区域(红色:整数最小二乘;蓝色:Bootstrap估计;黑色:直接取整估计) Fig. 1 The Voronoi diagrams of three popular integer estimators(red:integer least square;blue:Bootstrap;black:rounding) |
Bootstrap估计方法是基于序贯最小二乘原理,采用序贯取整方法直接获得整数模糊度值。该方法不但计算效率高,而且成功率容易计算,其成功率计算公式为[41, 42]
式中所要涉及的实数模糊度
 ∈N(a,
∈N(a, );
); 为Bootstrap估计整数模糊度值,a∈Zn;
为Bootstrap估计整数模糊度值,a∈Zn; 为式(21)中的
为式(21)中的 ,而有
,而有
对于模糊度搜索效率而言,尤其是采用SE-VB算法时[10],其首次获得的搜索半径即为Bootstrap解算的模糊度整数向量与实数向量之间的马氏距离。Bootstrapping成功率越高,表示Bootstrap解是整数最小二乘解的可能性越大,即Bootstrap解算的模糊度整数向量与实数向量之间的马氏距离值可能越接近最小,从而减小SE-VB算法的初始搜索半径的可能性越大,提高搜索效率的机会越多。当Bootstrapping成功率非常接近1时,且实数模糊度不存在偏差时,此时可以直接采用Bootstrap估计方法,无需搜索,其解算结果与整数最小二乘估计获得结果相同的概率也几乎接近1。
在格论中,Bootstrap估计方法获得的整数模糊度向量对应于格上最近平面算法获得格点—Babai点[10, 38, 43]。文献[38]指出通过LLL格基规约,可以提高Babai点近似比,即整数最小二乘估计的整数模糊度与实数模糊度之间的马氏距离与Bootstrap解算的整数模糊度与实数模糊度之间的马氏距离之比值。文献[25]基于BKZ格基规约,进一步提高了Babai点近似比。
由于式(26)为凸函数,文献[44]基于Prekopa定理推导出只有当 都相同时,此时的Bootstrapping成功率最大。同样由于降相关方法本身要求转换矩阵为幺模矩阵,降相关后
都相同时,此时的Bootstrapping成功率最大。同样由于降相关方法本身要求转换矩阵为幺模矩阵,降相关后 并不一定完全相同。比较式(16)与式(24),可知统一降相关比LLL格基规约可以获得
并不一定完全相同。比较式(16)与式(24),可知统一降相关比LLL格基规约可以获得 值更接近相同,可以得出统一降相关方法相对于LLL格基规约可以获得更高的Bootstrapping成功率。
值更接近相同,可以得出统一降相关方法相对于LLL格基规约可以获得更高的Bootstrapping成功率。
为了验证GNSS领域中模糊度降相关方法的性能,利用Delft 大学提供的Visual仿真软件,模拟GPS/Galileo/GLONASS/Compass卫星系统的长基线条件下的定位模型,即同时估计位置、对流层、电离层、模糊度参数,其余误差影响软件没有仿真,该软件只需模拟单个流动站的位置,即可模拟类似相对定位的解算方程式,计算出实数模糊度的方差协方差阵,由于是类似于精密单点定位模式仿真,基线长度对模糊度解算的影响较小,因而仿真软件中没有给出参考站位置。未来的4个卫星导航定位系统都将提供多频载波信号,而且都将采用码分多址技术,因此单个系统的相对定位原理及模糊度解算方法基本相同。由于其他3个卫星系统部分信号的频率与GPS的频率相对接近或相同,其模糊度解算成功率不会有太大差别,为便于数据模拟与分析,所有系统观测频率都设置为GPS系统的L1、L2、L5三个频率,从而可采用统一的相对定位数据处理模式。模拟的伪距噪声为0.3 m,模拟的载波相位噪声为0.003 m。由于Visual软件的单基线解算模式采用的数学模型无需设置两个测站,即可仿真相对定位的观测方程,因此文中仿真的测站为国际IGS武汉站,软件设置为单基线、单历元数据处理模式,同时估计电离层与对流层参数,截止高度角为5°。该模式类似于长基线数据处理模式,但是基线长度对共视卫星数的影响在软件中被忽去。基于最小二乘估计方法获得每个历元的模糊度实数值和其对应的方差协方差阵。分别采用LLL格基规约以及统一降相关,对模糊度的方差协方差阵及其逆矩阵(权阵)进行降相关处理,分析其对应的Bootstrapping成功率,并基于Monte Carlo方法估计整数最小二乘的成功率,其主要原理是由模糊方差协方差阵生成n个服从该分布的0均值样本,并采用模糊度搜索方法获得每个样本的整数模糊度值,其中正确解算的个数除以整个样本的个数即为整数最小二乘模糊度解算的成功率。如图 2所示,模拟的五维情况下,Monte Carlo方法获得的整数最小二乘的成功率,当样本个数大于400 000时,此时成功率接近收敛。该方法会耗费大量时间,不能满足实时导航定位的需要,本文仅它用来分析高维模糊度解算可能达到的成功率。图 3为仿真的4个系统的卫星轨迹图(2 h)。

|
| 图 2 Monte Carlo方法估计整数最小二乘成功率 Fig. 2 The ILS success rate estimated by Monte Carlo method |

|
| 图 3 卫星轨迹图 Fig. 3 The sky plot of satellites viewed |
表 1、2分别为基于方差协方差阵和权阵的不同格基规约方法获得的规约耗时、Bootstrapping成功率以及模糊度搜索耗时的均值。其中United规约表示统一降相关方法,LLL+United表示两种降相关方法的组合,即先对待规约的基进行LLL规约,然后再采用United规约处理,其中United规约处理的内部排序迭代次数可以人为设定,为了减少耗时,本文对于LLL+United规约处理中United内部排序迭代次数设定为1次。单独United规约处理的内部排序迭代次数没有预定值,其迭代终止条件是规约基满足式(23)与(24)。由表 1、2可知,格基规约可以显著提高模糊度解算的Bootstrapping成功率以及减少模糊度搜索耗时,当直接对模糊度搜索时,其平均耗时大于50 min,其Bootstrapping成功率接近于0。基于方差协方差阵的格基规约性能优于基于权阵的格基规约性能,可以获得更高的Bootstrapping成功率以及更少的模糊度搜索耗时的均值和规约耗时,其主要原因是模糊度方差协方差阵的元素值明显小于权阵的元素值,此时规约算法的执行次数将会减少,规约基之间的距离也相对更短。对于方差协方差阵的格基规约,United规约处理可以获得最高的Bootstrapping成功率(0.832 8),以及最少的模糊度搜索时间(0.147 7 s),但是会耗费较多的规约时间(6.453 8 s)。LLL+United规约的性能介于United规约与LLL规约之间,虽然其规约时间与搜索时间和0.999 1 s大于LLL规约的规约时间与搜索时间和(0.849 8 s)。但是由图 4可知,模糊度搜索耗时很不稳定 (0~6 s),相对于LLL规约,LLL+United规约可以明显提高模糊度搜索耗时稳定性。在表 1中,大的Bootstrapping成功率对应于少的模糊度搜索耗时,在表 2中,LLL+United规约的Bootstrapping成功率虽然大于LLL规约的Bootstrapping成功率,但是其模糊度搜索耗时要大于基于LLL规约的搜索耗时,其可能原因是模糊度搜索次数不仅与模糊度的方差协方差有关,而且也与模糊度实数值的小数部分有关,两者的综合影响导致其结果。
| 方差协方差 | LLL | LLL+United | United | 原始 |
| Bootstrapping 成功率 | 0.730 4 | 0.754 3 | 0.832 8 | 0 |
| 规约时间/s | 0.580 9 | 0.825 0 | 6.453 8 | N/A |
| 搜索时间/s | 0.268 9 | 0.174 1 | 0.147 7 | >50 min |

|
| 图 4 模糊度搜索时间(方差协方差阵) Fig. 4 The computation time for ambiguity search(variance and covariance) |
| 权矩阵 | LLL | LLL+United | United | 原始 |
| Bootstrapping 成功率 | 0.674 7 | 0.690 7 | 0.728 9 | N/A |
| 规约时间/s | 0.934 3 | 1.168 8 | 8.996 0 | N/A |
| 搜索时间/s | 1.850 9 | 1.906 4 | 1.457 8 | >50 min |
图 5为4个系统长基线、单历元采用不同规约方法后获得的Bootstrapping成功率,及其整数最小二乘成功率。由图 5可知,对于未来4个系统多频精密定位,可视卫星的个数将会增加到40个左右,模糊个数将会达到120个左右。相对于LLL规约,United规约可以整体提高模糊度解算的Bootstrapping成功率,但是由于模糊度之间的强相关性,尤其是电离层误差的影响,使得经United规约后的Bootstrapping成功率与整数最小二乘成功率之间仍然存在有较大的差值。

|
| 图 5 模糊度解算成功率(方差协方差阵) Fig. 5 The success rate of ambiguity resolution(variance and covariance) |
由图 5可知,对于未来多个系统多频精密长基线定位或精密单点定位,整数最小二乘成功率接近于1。意味着可单个历元解算出正确的整数模糊度值,从而有可能实现长基线、实时精密相对定位;或基于精密单点定位模糊度固定技术,实现全球、单站实时精密定位。这将会为测绘、农业等需要提供实时精密位置服务的领域带来新的机遇。但是对于多系统多频长基线相对定位或精密单点定位,高维模糊度快速解算及验证问题将会成为制约其广泛应用的关键问题[40, 45]。因此有必要进一步研究性能更好的格基规约方法,在消耗较少时间的同时,提高Bootstrapping成功率,减少模糊度的搜索时间。另一面需要深入研究快速的模糊度搜索方法、模糊度的可靠性检验等相关问题。再次,文中的试验分析是基于仿真的观测数据,理论分析模糊度解算方法的性能及其解算的成功率。在实际应用中,由于星座设计的不同、不同卫星系统频率差异、多路径误差、二阶电离层误差等影响,其实际解算模糊度的成功率与文中基于仿真数据获得的成功率会有一定的差别,因此需进一步结合实际观测数据验证模糊度解算的成功率。
8 结论本文分析了GNSS精密定位整数模糊度解算理论和方法的最近进展,引入格基规约方法用于GNSS模糊度解算,扼要介绍了格论的背景及其某些相关基础理论,分析了格基规约的性质;并将GNSS领域的多维Lagrange降相关、统一降相关等方法统一到格论框架下,从而对不同降相关方法的性能给出了理论解释;建议采用Bootstrapping成功率作为降相关的性能指标之一,因为他可以一定程度上反映模糊度的搜索效率,同时可提高实时模糊度解算的可靠性指标。针对GNSS精密定位的实际需要,指出可直接对模糊度的方差协方差进行格基规约。基于仿真数据,本文还比较分析了多频多系统长基线定位情况下,LLL规约与United规约用于模糊度解算的性能,结果表明:在高维情况下,United规约可以获得更高的Bootstrapping成功率,但是仍然与整数最小二乘成功率存在较大的差值。混合LLL规约与United规约方法可以有效融合两种方法的优点,减少两种方法的缺点。文章最后指出高维模糊度解算问题将会成为未来多频多系统GNSS精密定位的关键问题,有必要结合Bootstrapping成功率研究性能更好的格基规约方法。
| [1] | REMONDI B W.Pseudo-kinematic GPS Results Using the Ambiguity Function Method[J].Navigation:Journal of the Institute of Navigation,1991,38(1):17-36. |
| [2] | ABIDIN H Z.On the Construction of the Ambiguity Searching Space for On-the-fly Ambiguity Resolution[J].Navigation:Journal of the Institute of Navigation,1993,40(3):321-338. |
| [3] | FREI E,BEUTLER G.Rapid Static Positioning Based on the Fast Ambiguity Resolution Approach FARA:Theory and First Results[J].Manuscripta Geodaetica,1990,15(6):326-356. |
| [4] | CHEN D,LACHAPELLE G.A Comparison of the FASF and Least-squares Search Algorithms for on-the-fly Ambiguity Resolution[J].Navigation:Journal of The Institute of Navigation,1995,42(2):371-390. |
| [5] | TEUNISSEN P J G.Least-squares Estimation of the Integer GPS Ambiguities[C]//Proceedings of International Association of Geodesy General Meeting.Beijing:[s.n.],1993. |
| [6] | HAN S,RIZOS C.A New Method for Constructing Multi-satellite Ambiguity Combinations for Improved Ambiguity Resolution[C]//Proceedings of ION GPS-95:2.California:[s.n.],1995. |
| [7] | LI Z,GAO Y.Direct Construction of High Dimension Ambiguity Transformation for the Lambda Method[C]//Proceeding of KIS97.Banff:[s.n.],1997. |
| [8] | LIU L T,HSU H T,ZHU Y Z,et al.A New Approach to GPS Ambiguity Decorrelation[J].Journal of Geodesy,1999,73(10):478-490. |
| [9] | XU P.Random Simulation and GPS Decorrelation[J].Journal of Geodesy,2001,75(7):408-423. |
| [10] | CHANG X W,YANG X,ZHOU T.Mlambda:A Modified LAMBDA Method for Integer Least-squares Estimation[J].Journal of Geodesy,2005,79(9):552-565. |
| [11] | ZHOU Y M.A New Practical Approach to GNSS High-dimensional Ambiguity Decorrelation[J].GPS Solutions,2001,15(4):325-331. |
| [12] | XU P.Parallel Cholesky-based Reduction for the Weighted Integer Least Squares Problem[J].Journal of Geodesy,2012,86(1):32-52. |
| [13] | BORNO Mazen Al.Reduction in Solving Integer Least Square Problems[D].Quebec:McGill University,2011. |
| [14] | YU Xingwang.Multi-frequency GNSS Precise Positioning:Theory and Methods[D].Wuhan:Wuhan University,2011.(于兴旺.多频GNSS精密定位理论和方法研究[D].武汉:武汉大学,2011.) |
| [15] | LAGRANGE J L.Recherches D′arithmétique[J].Nouveaux Mémoires de l'Académie de Berlin,1773,265-312. |
| [16] | GAUSS C F.Disquisitiones Arithmeticae[M].Leipzig:[s.n.],1801. |
| [17] | HERMITE C,EXTRAITS de lettres de M,HERMITE M.Jacobi Sur Différents Objets de la Théorie des Nombres,Deuxiée Letter[J].J Reine AngewMath.1850(40):279-290. |
| [18] | KORKINE A,ZOLOTAREFF G.Sur les Formes Quadratiques[J].Math Annalen,1873,6(3):366-389. |
| [19] | MINKOWSKI H.Geometrie der Zahlen[M].Stuttgart:Teubner-Verlag,1896. |
| [20] | SCHARLAU W,OPOLKA H.From Fermat to Minkowski:Lectures on the Theory of Numbers and Its Historical Development[M].Berlin:Springer,1985. |
| [21] | KANNAN R.Improved Algorithms for Integer Programming and Related Lattice Problems[C]//Proceedings of the Fifteenth Annual ACM Symposium on Theory of Computing.New York:[s.n.],1983. |
| [22] | BETTINA H.Algorithms to Construct Minkowski Reduced an Hermite Reduced Lattice Bases[J].Theory Computation Science,1985,41(2):125-139. |
| [23] | AJTAI M.The Shortest Vector Problem in L2 is NP-hard for Randomized Reductions[C]//Proceedings of the Thirtieth Annual ACM Symposium on the Theory of Computing.Texas:[s.n.],1998,10-19. |
| [24] | LENSTRA A K,LENSTRA H W Jr,LOVSZ L.Factoring Polynomials with Rational Coefficients[J].Mathematische Annalen,1982,261(4):515-534. |
| [25] | SCHNORR C P,EUCHNER M.Lattice Basis Reduction:Improved Practical Algorithms and Solving Subset Sum Problems[J].Mathematical Programming,1994,66(2):181-199. |
| [26] | PHONG N Q,BRIGITTE V.The LLL Algorithm:Survey and Applications[M].Berlin:Springer,2010. |
| [27] | HASSIBI A,BOYED S.Integer Parameter Estimation in Linear Models with Applications to GPS[J].IEEE Trans Signal Processing,1998,46(11):2938-2952. |
| [28] | CHANG X W,ZHOU T.Miles:Matlab Package for Solving Mixed Integer Least Squares Problems[J].GPS Solutions,2007,11(4):289-294. |
| [29] | JAZAERI S,AMIRI-SIMKOOEI A R,SHARIFI M A.Fast Integer Least-Squares Estimation for GNSS High Dimensional Ambiguity Resolution Using Lattice Theory[J].Journal of Geodesy,2012,85(12):1-14. |
| [30] | TEUNISSEN P J G.A New Method for Fast Carrier Phase Ambiguity Estimation[C]//Proceedings of the IEEE PLANS'94.Las Vegas:[s.n.],1994. |
| [31] | XU P,CANNON E,LACHAPELLE G.Mixed Integer Programming for the Resolution of GPS Carrier Phase Ambiguities[C]//IUGG 95 Assembly.Boulder:[s.n.],1995. |
| [32] | CASSELS.An Introduction to the Geometry of Numbers[M].Berlin:Springer,1997. |
| [33] | CHANG X W,YANG X,LE-NGOC T,et al.Partial Regularization Approach for Detection Problems in Underdetermined Linear Systems[J].IET Communications,2009,3(1):17-24. |
| [34] | SCHNORR C P.Blockwise Lattice Basis Reduction Revisited[C]//Codes and Lattices in Cryptography.Darmstadt:[s.n.],2006. |
| [35] | LING Cong,WAI H M.A Unified View of Sorting in Lattice Reduction:From V-BLAST to LLL and Beyond[C]//Proceedings of IEEE Information Theory Workshop 2009.Taormina:[s.n.],2009. |
| [36] | SEYSEN M.Simultaneous Reduction of a Lattice Basis and Its Reciprocal Basis[J].Combinatorica,1993,13(3):363-376. |
| [37] | JOHANNES B.Closest Vectors,Successive Minima,and Dual HKZ-Bases of Lattices[C]//Proceedings of the 27th International Colloquium on Automata,Languages and Programming.Geneva:[s.n.],2000. |
| [38] | BABAI L.On Lovász Lattice Reduction and the Nearest Lattice Point Problem[J].Combinatorica,1986,6(1):1-13. |
| [39] | AGRELL E,ERIKSSON T,VARDY A,et al.Closest Point Search in Lattices[J].IEEE Trans Inform Theory,2002,48(8):2201-2214. |
| [40] | XU P.Voronoi Cells,Probabilistic Bounds,and Hypothesis Testing in Mixed Integer Linear Models[J].IEEE Transactions on Information Theory,2006,52(7):3122-3138. |
| [41] | TEUNISSEN P J G.Success Probability of Integer GPS Ambiguity Rounding and Bootstrapping[J].Journal of Geodesy,1998,72(10):606-612. |
| [42] | TEUNISSEN P J G.An Optimality Property of the Integer Least-squares Estimator[J].Journal of Geodesy,1999,73(11):587-593. |
| [43] | XU Peiliang,SHI Chaung,LIU Jingnan.Integer Estimation Methods for GPS Ambiguity Resolution:an Applications Oriented Review and Improvement[J].Survey Review,2012,43(324):59-71. |
| [44] | TEUNISSEN P J G.An Invariant Upper Bound for the GNSS Bootstrapping Ambiguity Success Rate[J].Journal of Global Positioning Systems,2003,2(1):13-17. |
| [45] | TEUNISSEN P J G,VERHAGEN S.GNSS Carrier Phase Ambiguity Resolution:Challenges and Open Problems[C]//Observing our Changing Earth:Proceedings of the 2008 IAG General Assembly,Berlin:Springer,2008. |