插值参数是构成插值算法的基本元素,包括搜索方式和插值核函数。不同的插值参数产生不同的插值结果,甚至存在巨大差异[1]。但是对于普通用户而言,选择合适的插值参数是困难的,直接导致空间插值成为一个“黑箱(black box)”,因此稳健的插值算法应提供可以理解的插值参数,或者给用户尽可能多的插值参数提示信息[2]。
文献[3]通过试验给出了不同插值算法的最佳搜索点数试验值。文献[4]认为克里格插值算法几乎不受搜索点数的影响,而加权平均插值算法却严格依赖于搜索点数。对于反距离加权插值算法中的权指数取值而言,文献[5]认为取1或2比较合适,但文献[6]却认为取2将取得更好的试验效果。对于径向基函数插值算法中的光滑因子取值而言,虽然没有普遍认可的确定方法,但也有相关文献提出了各种方法:文献[7, 8, 9]提出了数值近似表达的方法;文献[10]提出了基于交叉验证的统计方法;文献[11]提出了使用递归算法寻找使得插值表面全局误差最小的方法;文献[12]认为多重二次曲面和多重对数径向基函数应使用接近于零的光滑因子,反多重二次曲面、自然三次样条和薄板样条径向基函数则应使用非常大的光滑因子。
多数学者在选择插值参数时,大多是依赖经验直接指定。如文献[12/a>]在研究地貌类型、采样密度和插值算法对规则格网精度的影响时,使用8个搜索点数完成径向基函数和反距离加权插值算法的计算;文献[13]在反距离加权插值算法自适应研究中,规定“邻域”指距离插值点最近的5个采样点组成的局部范围;文献[14]以距离插值点最近的格网点为中心,并以周围8个格网点完成似大地水准面格网双二次多项式插值方法的研究。但是仅依赖于经验确定取值,势必会造成插值结果的不确定性,甚至会导致空间分布的扭曲模型,做出潜在的错误决策[15]。
为此,本文根据插值算法最优权重确定方法的差异,选取反距离加权插值算法(inverse distance weighted,IDW)、径向基函数插值算法(radial basis functions,RBF)和普通克里格插值算法(ordinary Kriging,OK)的相关插值参数,进行插值参数的“优选”问题研究。首先阐述插值参数的含义,分析不同参数对DEM插值精度的影响,并选择搜索点数、搜索方向和插值核函数因子作为试验对象;然后选择6种不同地貌类型地区的稀疏分布的离散采样点作为试验数据源;最后利用交叉验证法、相关分析法、趋势面分析法和方差分析法等一系列试验方法,计算得到相关插值参数的“最优”取值区间,消除参数选择的随意性。
2 插值参数 2.1 搜索方式
对于绝大多数DEM插值算法而言,需要在邻域范围内完成插值点的高程计算,即以插值点为中心,确定一定尺寸的邻域(或是矩形邻域,或是圆形邻域),然后选择已知采样点完成插值计算,这一过程称为采样点的搜索方式。其控制选项包括:搜索形状、搜索方向、搜索点数、搜索邻域半径以及搜索时是否考虑等高线、结构线、断裂线或边界线,等等。搜索方式决定了采样点的选择,最终导致不同数量、分布方式的采样点影响着DEM的插值精度。
2.2 插值核函数
插值核函数指插值算法内部调节采样点对插值点权重影响的数学函数,是影响DEM插值精度的重要因素之一[16]。插值核函数都是显式或隐式的距离函数(表 1),其地理意义直接或间接地表达了相邻两个空间对象之间的相关关系[1]。插值核函数因子是插值算法的关键因子,可能导致插值精度的提高,也可能导致插值精度的降低。
| 核函数 | 表达式(d为距离) | 核函数因子 |
| 反距离加权 (IDW) | p(d)=(d+t)-u | u为权指数; t为光滑因子 |
| 多重二次曲面 函数(MQF) |
 | |
| 反多重二次曲面 函数(IMQF) |
 | |
| 多重对数函数 (MLF) | φ(d)=ln(d2+c2) | |
| 薄板样条函数 (TPSF) | φ(d)=(d2+c2)ln(d2+c2) | |
| 自然双三次样条 函数(NCSF) | φ(d)=(d2+c2)3/2 | c为光滑因子 |
| 线性函数 (LINE) | γ(d)=C0+Cd | |
| 球形函数 (SPHERE) |  | |
| 指数函数 (EXP) |
 | |
| 高斯函数 (GAUSS) |  | C0为块金值; C为拱高; a为变程 |
不同的插值参数产生不同的DEM插值精度。有些插值参数可能确定性优化或者确定性降低DEM插值精度,如插值过程中将等高线、结构线、断裂线或边界线等作为限制条件,本质是选择分布位置更为合理的采样点的问题,最终确定性提高DEM插值精度。对于等高线而言,如果跨越等高线选择其他等高线上的采样点,将导致地形的“块纹”现象[17]。对于结构线、断裂线、边界线而言,异侧的采样点存在地貌突变现象,如果参与插值计算,必将有损于DEM插值精度[18,19]。又如反距离加权插值算法中的光滑因子t,其主要作用是平滑地形,使用不为零的光滑因子,直接导致山顶高程被降低,山谷高程被抬高,最终降低DEM插值精度。
另一些插值参数因地貌类型、采样点分布方式的差异,选择不同取值可能优化或降低DEM插值精度。如搜索方向、搜索点数(或搜索半径)、反距离加权插值算法中的权指数u、径向基函数插值算法中的光滑因子c、克里格插值算法中的半变异函数的块金值C0、拱高C、变程a。
因此,本文总结了几种典型DEM插值算法中的对插值精度具有显著影响的参数,作为DEM插值参数“优选”试验的研究对象。
3 DEM插值参数“优选”试验 3.1 试验数据来源及特征采样点数据获取的采样策略包括沿等高线采样、规则格网采样、渐进采样、选择性采样以及混合采样等,实践中应当根据不同的情况采用不同的数据采样策略[19]。因此,为不失一般性,本文选择具有代表性的6种不同地貌类型的地区作为试验区域,其面积均为15km×15km;试验数据来源于30m分辨率的ASTER GDEM,对其进行离散化处理得到稀疏分布的离散采样点作为试验数据源,其图形特征如图 1所示(见文末),地形描述参数如表 2所示。

|
| 图 1 试验区域透视效果图 Fig. 1 Perspective rendering of experimental regions |
| 地貌类型 | 平原 | 丘陵 | 低山 | 中山 | 高山 | 混合 |
| 所属区域 | 江苏 | 山东 | 河南 | 贵州 | 西藏 | 辽宁 |
| 最低高程/m | 2 | 33 | 285 | 1235 | 3940 | 575 |
| 最高高程/m | 50 | 354 | 1444 | 2252 | 5769 | 1081 |
| 平均坡度/(°) | 1.27 | 5.51 | 13.36 | 16.63 | 23.77 | 9.11 |
试验选取反距离加权插值算法、径向基函数插值算法、普通克里格插值算法中的相关插值参数为研究对象,试验取值如表 3所示。
| 插值算法 | 搜索方向 | 搜索点数 | 核函数因子 | |
| 加权 平均 | IDW | D= 无方向、 四方向、 八方向 | P=1、2、 3、4、5、6、 7、8 | u=1、2、3、4、5 |
| 径向 基函 数 |
MQF | c=0、20、40、 60、80、100、 200、300、400、 500、600、700、 800、900、1000 | ||
| IMQF | ||||
| MLF | ||||
| TPSF | ||||
| NCSF | ||||
| 普通 克里 格 |
LINE | 试验拟合 | ||
| SPHERE | ||||
| EXP | ||||
| GAUSS | ||||
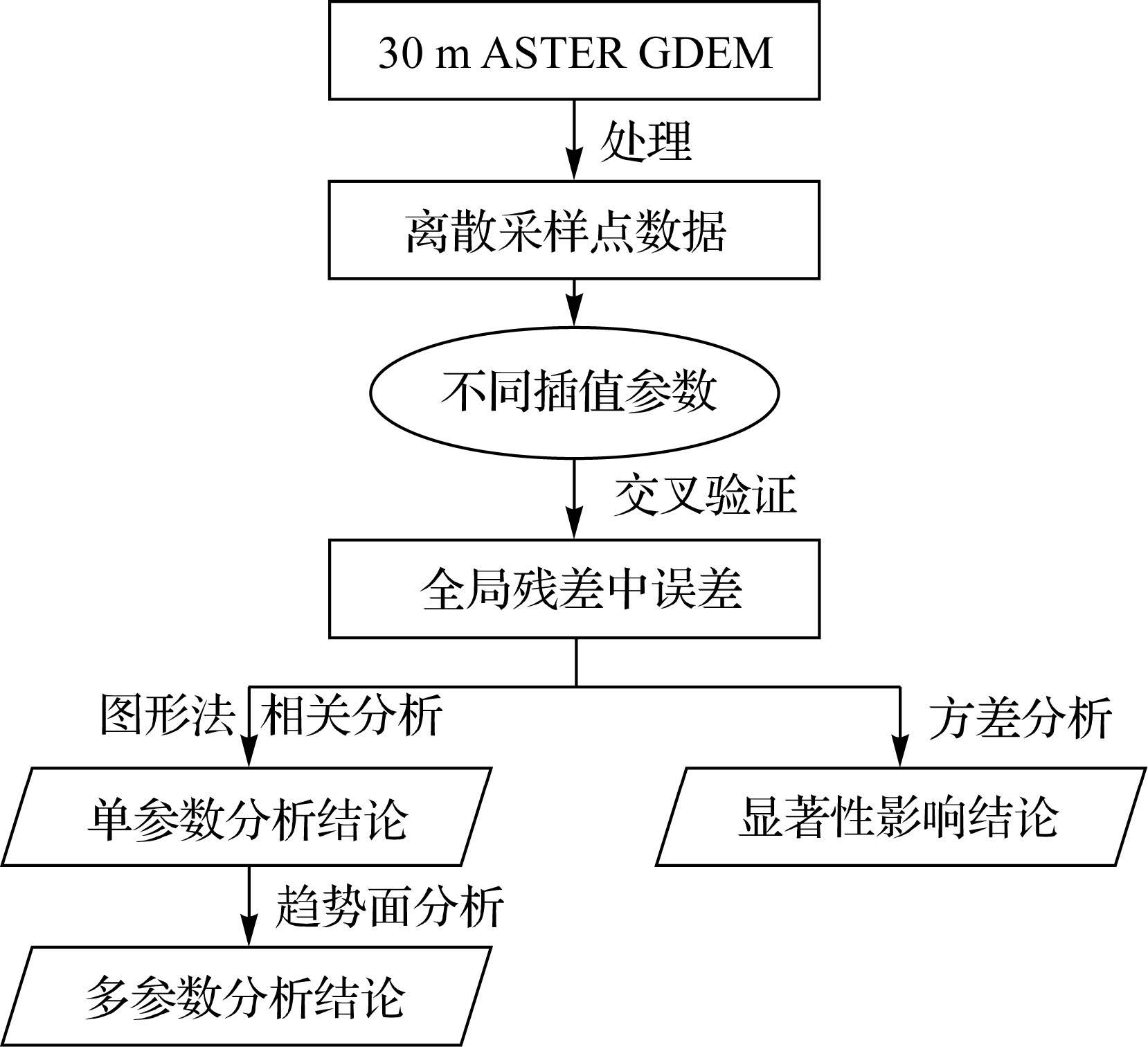
DEM插值参数“优选”试验的流程如图 2所示。
|
| 图 2 DEM插值参数“优选”试验流程图 Fig. 2 Flow chart of experiment |
第1步:试验数据获取。
选取6种不同地貌类型区域的15km×15km范围内的30m分辨率的ASTER GDEM,离散化后作为试验数据源;
第2步:运用交叉验证法统计全局残差中误差值。
交叉验证法是一种与用户无关、与DEM格网尺寸无关的试验方法,可以让用户将关注点集中于插值参数本身。
试验中根据插值算法中不同插值参数的不同试验取值,运用交叉验证法计算每一采样点的残差值,并统计全局残差中误差值。然后以此为基础,运用各种分析方法确定插值参数的“最优”取值区间。以反距离加权插值算法为例,按照表 3的插值参数试验取值,计算得到不同插值参数组合时的全局残差中误差值,如表 4所示。
| 试验区域 | 搜索方向 | 搜索点数 | 权指数 | 全局残差 中误差值/m |
| 河南 | 无方向 | 4 | 1 | 4.0395 |
| 无方向 | 4 | 2 | 3.8173 | |
| 无方向 | 4 | 3 | 3.9381 | |
| 无方向 | 4 | 4 | 4.2175 | |
| 无方向 | 4 | 5 | 4.5324 | |
 |  |  | 
| |
| 四方向 | 4 | 1 | 2.6117 | |
| 四方向 | 4 | 2 | 2.7171 | |
| 四方向 | 4 | 3 | 3.3429 | |
| 四方向 | 4 | 4 | 3.9300 | |
| 四方向 | 4 | 5 | 4.4064 |
第3步:基于全局残差中误差值,运用相关分析和图形法选择插值参数的“最优”取值区间相关分析是经典统计分析中最基本的方法,从统计分析角度定量分析要素之间的相关程度和拟合变量之间的数量关系。要素之间相关程度的测定,主要通过相关系数r的计算与检验完成。一般认为,当相关系数r的绝对值大于0.8时,表明两变量之间具有较强的线性关系;当相关系数r的绝对值小于0.3时,表明两变量之间的相关关系较弱[20]。
试验中运用相关分析法分析不同搜索方向时计算得到的中误差值之间的相关关系,确定搜索方向对DEM插值精度的影响,并选择“最优”的搜索方向。表 5中不同搜索方向之间的相关系数均在0.83以上,特别是四方向和八方向的相关系数高达0.99以上(表中“D1×D2”表示四方向和八方向搜索时计算得到的中误差值之间的相关系数值),表明四方向和八方向搜索对DEM插值精度的影响不大。
| 试验区 | 江苏 | 山东 | 河南 | 贵州 | 西藏 | 辽宁 |
| D0×D1 | 0.9591 | 0.9901 | 0.9293 | 0.9524 | 0.8774 | 0.9783 |
| D0×D2 | 0.9584 | 0.9915 | 0.9083 | 0.9395 | 0.8358 | 0.9761 |
| D1×D2 | 0.9980 | 0.9994 | 0.9982 | 0.9989 | 0.9963 | 0.9997 |
如果结合相同搜索点数、插值核函数因子时不同搜索方向对应的中误差柱形图(图 3),可以发现:无方向限制搜索时建立的DEM插值精度最差,四方向搜索和八方向搜索相当,因此,综合考虑插值算法的插值效率和插值精度的前提下尽量使用四方向搜索。
第4步:基于全局残差中误差值,运用趋势面分析法验证插值参数的“最优”区间。
趋势面分析是利用数学函数模拟要素在空间上的分布及其变化趋势的方法,本质是通过回归分析,运用最小二乘拟合二维非线性函数,模拟要素在空间上的分布规律,展现要素在空间上的变化趋势[21]。
假设存在采样点(xi,yi,zi)(i=1,2,…,n),拟合回归方程z=fx,y,使得
其中常用的f是多项式函数,因为任何函数在适当范围内都可以用多项式函数逼近,并且可以根据需要调整多项式函数的次数。此外,需要用F检验来检验拟合得到非线性函数的适度问题,因为它直接关系趋势面分析的应用效果。

|
| 图 3 搜索方向对DEM插值精度的影响(基于IDW) Fig. 3 Influence of search directions on DEM interpolation accuracy(based on IDW) |
试验中运用趋势面分析法分析不同插值参数对DEM插值精度的影响,从空间分布趋势角度确定插值参数的“最优”取值区间。表 6(见文末)中以搜索点数为x轴、光滑因子为y轴、中误差为z轴进行三次多项式趋势面分析,从空间连续变化的角度观察搜索点数、光滑因子对DEM插值精度的影响趋势。可以发现:搜索点数、光滑因子对中误差的趋势面函数拟合程度极高,可决系数(R2)达到0.9283;查F分布表得F0.05(9,95)=1.96小于计算F值(158.3158),表明三次趋势面拟合函数在0.05的置信水平下是显著的。其次从趋势面拟合效果图中可以清楚地看到,中误差较小的区域集中在搜索点数20~24点之间且光滑因子接近于0;中误差较大的区域集中在光滑因子较大或搜索点数44~56点之间。
| 试验区域 | 河南 |
| 拟合效果图 | 
|
| F值 | 158.3158 |
| p值 | 0 |
| R2值 | 0.9283 |
第5步:基于全局残差中误差值,运用方差分析法研究各插值参数的显著性差异。
方差分析用于两个或两个以上样本均数差别的显著性检验,研究不同因素的变异对总变异的贡献大小,并分析不同水平的控制因素是否对结果产生了显著性影响[22]。方差分析的p值常用于推断控制因素显著性影响程度的指标,假设给定置信水平0.05,当计算得到的p值小于或等于0.05时,可以认为控制因素对试验结果存在显著性影响。
试验中运用方差分析法分析插值参数对DEM插值精度的显著性影响程度,提示用户改进哪个参数可以更有效地改善插值效果。
表 7中,如果考虑半变异函数模型和搜索点数对DEM插值精度的影响,则半变异函数模型及两者的交互作用对DEM插值精度都具有显著性影响(即p<0.05),而搜索点数对DEM插值精度不具有显著性影响(即p=0.3202>0.05);考虑搜索方向和搜索点数对DEM插值精度的影响,则搜索点数对DEM插值精度具有显著性影响,而搜索方向和两者交互作用不具有显著性影响;考虑半变异函数模型和搜索方向对DEM插值精度的影响,则半变异函数模型对DEM插值精度具有显著性影响,而搜索方向和两者交互作用不具有显著性影响。因此,可以认为三因素对DEM插值精度的显著性影响程度的顺序为“半变异函数模型>搜索点数>搜索方向”,其中搜索方向对DEM插值精度不具显著性影响。
| 试验区域 | 变异来源 | 平方和(SS) | 自由度(DF) | 均方(MS) | F值 | p值 |
| 山东 | “半变异函数模型”间 | 311.2466 | 3 | 103.7489 | 19.6530 | 0.0001 |
| “搜索点数”间 | 27.7214 | 4 | 6.9304 | 1.3130 | 0.3202 | |
| 半变异函数模型×搜索点数 | 63.3495 | 12 | 5.2791 | 110.1900 | 0.0000 | |
| “搜索方向”间 | 0.0092 | 2 | 0.0046 | 0.2050 | 0.8188 | |
| “搜索点数”间 | 0.6181 | 4 | 0.1545 | 6.8580 | 0.0106 | |
| 搜索方向×搜索点数 | 0.1803 | 8 | 0.0225 | 0.0220 | 1.0000 | |
| “半变异函数模型”间 | 39.5234 | 3 | 13.1745 | 346.4100 | 0.0000 | |
| “搜索方向”间 | 0.0092 | 2 | 0.0046 | 0.1210 | 0.8878 | |
| 半变异函数模型×搜索方向 | 0.2282 | 6 | 0.0380 | 0.2390 | 0.9612 |
按照第3节的描述,本文运用一系列试验方法,计算得到了几种典型DEM插值算法中插值参数的“最优”取值区间,如表 8所示。结合插值算法的特性分析验结果,探索插值参数的“优选”规律,以便更好地指导DEM建模的运用。
| 插值算法 | 搜索点数 | 搜索方向 | 插值核函数因子 | 各因素影响程度 | |
| 加权平均 | IDW | P=4-12 | D=四方向 | u=2-3 | 权指数>搜索点数>搜索方向 |
| 径向基函数 | MQF | P=24-32 | D=四方向 | c=0-200 | 搜索点数>光滑因子>搜索方向 |
| IMQF | P<12 | D=四方向 | c=1000或极大 | — | |
| MLF | P=20-24 | D=四方向 | c=0 | 搜索点数>光滑因子>搜索方向 | |
| TPSF | P>32 | D=四方向 | c=0 | 光滑因子>搜索点数>搜索方向 | |
| NCSF | P>32 | D=四方向 | c=0 | 光滑因子>搜索点数>搜索方向 | |
| 克里格 | LINE | P=8-16 | D=无方向 | 块金值较小 | 半变异函数模型 >搜索点数>搜索方向 |
| SPHERE | P=8-16 | ||||
| EXP | P=8-16 | ||||
| GAUSS | P=4-8 |
反距离加权插值算法是一种精确性插值算法,插值生成的最大值和最小值只会出现在采样点处,随着搜索点数的增加,采样点间的高差逐渐增大,最终导致插值精度降低,因此较少的搜索点数是合适的选择(图 4)。
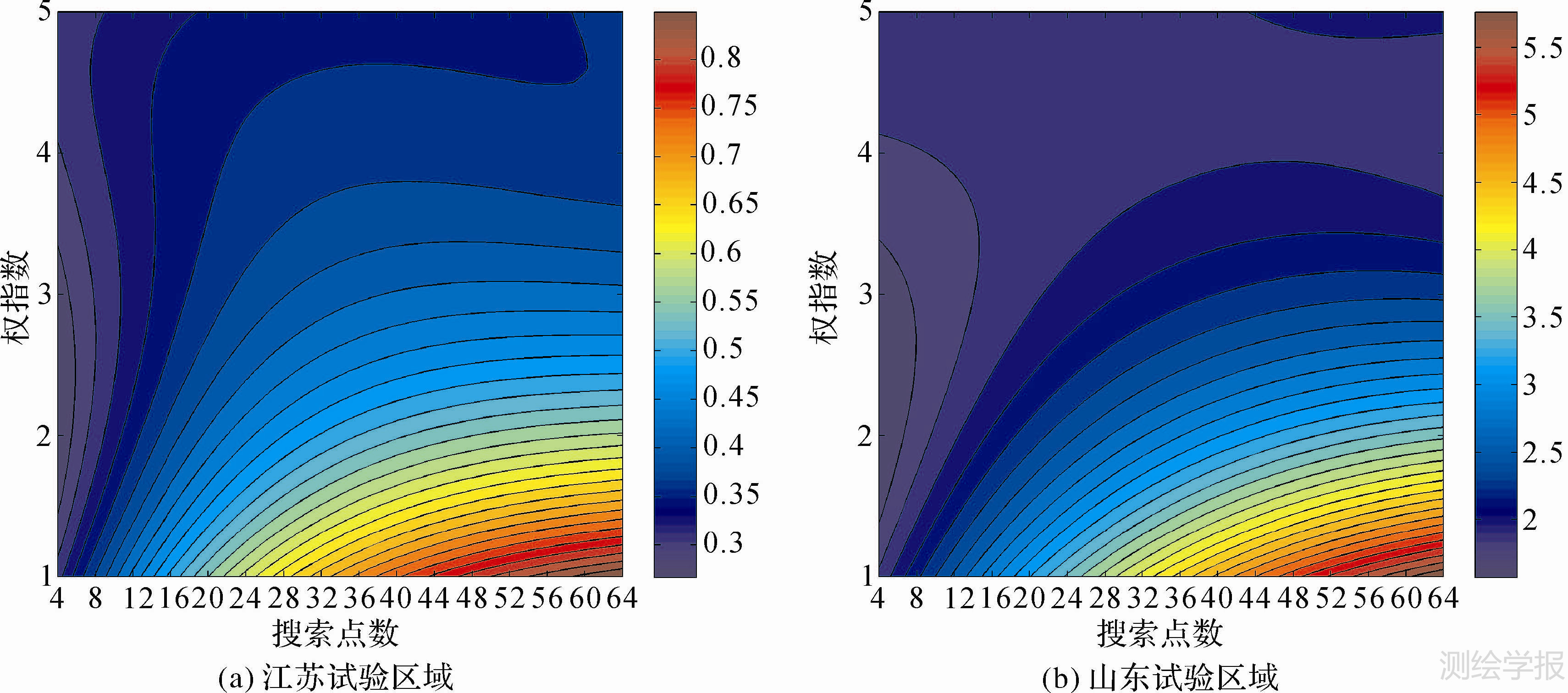
|
| 图 4 趋势面分析结果(基于反距离加权插值算法) Fig. 4 Results of trend surface analysis(based on IDW) |
其次随着权指数u的增加,每一采样点对插值点的权重影响的敏感程度增加,表现在距离较近的采样点的贡献率显著增加,而距离较远的采样点的贡献率逐渐降低,因此较大或较小的权指数都不是理想的选择。更为重要的是,试验结果表明权指数、搜索点数和搜索方向三参数对DEM插值精度影响程度为“权指数>搜索点数>搜索方向”,因此适时改变权指数可以更明显地提高插值精度。
径向基函数插值算法同样是一种精确性插值算法,与反距离加权插值算法相比,它可以计算出高于或者低于采样点的高程值,因此搜索点数的选择和反距离加权插值算法存在差异。MQF和MLF的“最优”取值区间在20~32点之间或大于64点(考虑插值效率取小值更为合适)(图 5),IMQF的“最优”取值区间小于12点,TPSF和NCSF的“最优”取值区间大于32点。这和其他研究成果都不一致,特别是TPSF和NCSF,当搜索点数大于32点时,几乎可以获得最佳的插值结果。其次,径向基函数插值算法的核函数属于典型的对称性距离函数,因此使用较少搜索方向可能导致较差的插值精度。第三,径向基函数插值算法的核函数中光滑因子是影响插值精度的重要参数之一,光滑因子的“最优”取值区间也和Aguilar的研究成果存在较大差异。对于MQF、MLF而言,较小的光滑因子是合适的;对于IMQF而言,需要选择极大的光滑因子,较小的光滑因子导致极大的数值不稳定性;对于TPSF、NCSF而言,当搜索点数较少时,TPSF、NCSF产生显著的数值不稳定性,随着光滑因子的增加,这种数值不稳定性消失;当搜索点数较大(>32)时,TPSF、NCSF插值的数值不稳定性消失,可以得到最佳的插值结果,但是随着光滑因子的增加,数值不稳定性逐渐表现出来,可能这就是为什么Aguilar认为需要使用极大光滑因子的原因。同样,试验结果表明光滑因子、搜索点数和搜索方向三参数对DEM插值精度影响程度因径向基函数的差异而有不同表现(表 8):对于MQF、MLF而言,搜索点数的影响程度更高;对于TPSF、NCSF而言,光滑因子的影响程度更高;而对于IMQF而言,由于插值结果的数值不稳定性,无法判断各参数的影响程度高低。

|
| 图 5 趋势面分析结果(基于MQF径向基函数插值算法) Fig. 5 Results of trend surface analysis(based on MQF RBF) |
普通克里格插值算法在插值过程中需要根据试验数据建立试验半变异函数,即选择合适的半变异函数模型及其拟合值。如果试验数据不存在合适的试验半变异函数,将导致不能得到理想的插值结果[23],因此半变异函数模型对DEM插值精度具有最大的显著性影响。同时试验还表明:第一,线性模型始终具有稳定的插值结果,而且随着搜索点数的增大,中误差值呈现逐步衰减并趋于稳定的趋势。第二,在所有半变异函数模型中,块金值的作用异常明显。当块金值为0或较小时,指数模型的插值结果和线性模型几乎一致,且插值中误差较小;当块金值较大时,则插值中误差较为明显(图 6)。显然和块金值的含义存在很大关系,即块金值代表的是离散采样点集中的取样误差和小尺度变化引起的误差等[23]。第三,克里格插值算法的一个重要特性是屏蔽效应[25],可以消除较多搜索点数和搜索方向对DEM插值精度的影响,因此较少搜索点数和无方向限制搜索是合理的取值。

|
| 图 6 不同半变异函数时搜索点数和DEM插值误差的关系 Fig. 6 Results of trend surface analysis |
本文运用交叉验证法、相关分析、趋势面分析和方差分析等方法研究了几种典型插值算法的插值参数的“最优”取值区间。由于DEM插值过程中,并没有任何一个方法可以实现地形特征的自动判别,并选择适宜的插值算法和相应插值参数,因此向用户提供更多的插值参数提示信息,消除插值参数选择的随意性,就显得尤为重要。其次,试验过程中并没有考虑某些特殊取样可能对某些插值算法产生的“异常”影响,如IMQF、TPSF、NCSF等插值残差中存在的极大值,因此通过全局残差中误差计算得到的插值参数“最优”取值区间,在稳健型、抗差性方面是“最优”的选择。再次,搜索方向作为影响DEM插值精度的因素之一,和其他因素相比较而言,其影响程度最低。并随着InSAR、LiDAR等新型的数据获取手段的出现[19],使得获取的采样点精度不断提高、分布日益密集,因此在实际建模过程中可以淡化,甚至忽略搜索方向的选择。
不同插值算法的插值参数是不同的,因此如何确定其他插值算法的插值参数“优选”区间是下一步研究试验工作,即将现有算法进行合理的分类,并得出各种插值算法的参数“优选”规律,将能更好地指导DEM建模的运用。
| [1] | LU Huaxing.Research on DEM Error Model[D].Nanjing: Nanjing Normal University,2008. (卢华兴.DEM误差模型研究[D].南京:南京师范大学,2008.) |
| [2] | HOFIERKA J,CEBECAUER T,U 'RI M.Optimisation of Interpolation Parameters Using a Cross-validation [J].Earth Surface Processes and Landforms,2005,30(4):461-477. |
| [3] | WANG Jiayao.Principles of Spatial Information System[M]. Beijing:Science Press,2001.(王家耀.空间信息系统原理[M].北京:科学出版社,2001.) |
| [4] | GAO J.Construction of Regular Grid DEMs from Digitized Contour Lines:A Comparative Study of Three Interpolators[J].Geographic Information Sciences,2001,7(1):8-15. |
| [5] | LAM N S.Spatial Interpolation Methods: A Review[J]. The American Cartographer,1983,10(2):129-149. |
| [6] | F A N D.Interpolation Methods for Scattered Sample Data: Accuracy, Spatial Patterns, Processing Time[J]. Cartography and Geographic Information Systems,1996,23(3):128-144. |
| [7] | HARDY R L.Multiquadric Equations of Topography and Other Irregular Surfaces[J].Journal of Geophysical Research,1971,76(8):1905-1915. |
| [8] | FRANKE R.Scattered Data Interpolation: Tests of Some Methods[J]. Mathematics of Computation,1982,38(157):181-200. |
| [9] | FOLEY T A.Interpolation and Approximation of 3-D and 4-D Scattered Data[J]. Computers & Mathematics with Applications,1987,13(8):711-740. |
| [10] | LI J, CHEN C S. A Simple Efficient Algorithm for Interpolation between Different Grids in Both 2D and 3D[J]. Mathematics and Computers in Simulation, 2002,58(2): 125-132. |
| [11] | RIPPA S.An Algorithm for Selecting a Good Value for the Parameter C in Radial Basis Function Interpolation[J].Advances in Computational Mathematics,1999,11(2-3):193-210. |
| [12] | AGUILAR F J,AGVERA F,AGUILAR M A,et al.Effects of Terrain Morphology, Sampling Density and Interpolation Methods on Grid DEM Accuracy[J].Photogrammetric Engineering & Remote Sensing,2005,71(7):805-816. |
| [13] | GEORGE Y L,DAVID W W.An Adaptive Inverse Distance Weighting Spatial Interpolation Technique[J].Computers & Geosciences,2008,34(9):1044-1055. |
| [14] | DENG Xingsheng,GUO Yunkai,HUA Xianghong.Quasigeod Grid Network Biquadratic Interpolation Method[J].Acta Geodaetica et Cartographica Sinica,2009,38(1):35-40.(邓兴升,郭云开,花向红.似大地水准面格网双二次多项式插值方法[J].测绘学报,2009,38(1) :35-40.) |
| [15] | LONGLEY P A,GOODCHILD M F,MAGUIRE D J,et al.Geographical Information Systems: vol 1: Principles and Technical Issues[M]. 2nd ed.New York: John Wiley & Sons,1999. |
| [16] | SMITH de M J,GOODCHILD M F,LONGLEY P A.Geospatial Analysis: A Comprehensive Guide to Principle, Techniques and Software Tools[M].2nd ed. London: The Winchelsea Press,2007. |
| [17] | GAO Jun,XIA Yunjun,YOU Xiong,et al.Virtual Reality in Terrain Environment Simulation[M].Beijing:PLA Publishing House,1999. (高俊,夏运均,游雄,等.虚拟现实在地形环境仿真中的应用[M].北京:解放军出版社,1999.) |
| [18] | TANG Guoan,LIU Xuejun,LV Guonian.Principle and Method of DEM and Geoscience Analysis[M].Beijing:Science Press,2005.(汤国安,刘学军,闾国年.数字高程模型及地学分析的原理与方法[M].北京:科学出版社,2005.) |
| [19] | LI Zhilin,ZHU Qing.Digital Elevation Model[M].2nd ed. Wuhan:Wuhan University Press,2003.(李志林,朱庆.数字高程模型[M].第2版. 武汉:武汉大学出版社,2003.)[20] XU Jianhua.Geographical Modelling Methods[M].Beijing:Science Press,2010.(徐建华.地理建模方法[M].北京:科学出版社,2010.) |
| [20] | XU Jianhua.Geographical Modelling Methods[M].Beijing:Science Press,2010.(徐建华.地理建模方法[M].北京:科学出版社,2010.) |
| [21] | TANG Qiyi.DPS Data Processing System: Experimental Design, Statistical Analysis and Data Mining[M].Beijing:Science Press,2007.(唐启义.DPS数据处理系统: 实验设计、统计分析及数据挖掘[M].北京:科学出版社,2007.) |
| [22] | LIU Xianzhao,ZHANG Anding,LI Jiazhu.Geographical Mathematics Methods[M].Beijing:Science Press,2009.(刘贤赵,张安定,李嘉竹.地理学数学方法[M].北京:科学出版社,2009.) |
| [23] | ZIMMERMAN D,PAVLIK C,RUGGLES A,et al.An Experimental Comparison of Ordinary and Universal Kriging and Inverse Distance Weighting[J].Mathematical Geology,1999,31(4):375-390. |
| [24] | ZHANG Jinxiong.Scale, Uncertainty and Integration of Spatial Information[M].Wuhan:Wuhan University Press,2008.(张景雄.空间信息的尺度、不确定性与融合[M].武汉:武汉大学出版社,2008.) |
| [25] | ZHOU Chenghu,PEI Tao.Principle of Spatial Analysis in Geographic Information System[M].Beijing:Science Press,2011.(周成虎,裴韬.地理信息系统空间分析原理[M].北京:科学出版社,2011.) |


