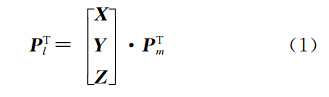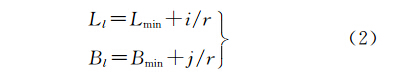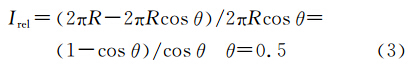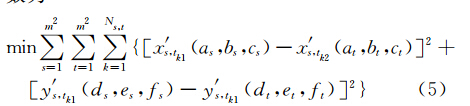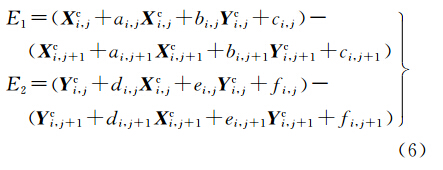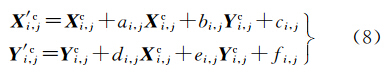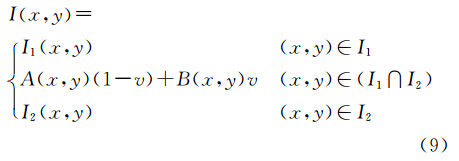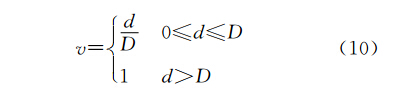1 引 言
我国于2010年10月发射了嫦娥二号(CE-2)探月卫星,嫦娥二号绕月飞行期间,传回了覆盖全月球的海量月表高清影像,分辨率达到7 m。嫦娥二号携带一台双线阵推扫式CCD相机[1],有前视和后视两个线阵,两个线阵成一定角度对月拍摄,形成立体影像。由两个线阵的影像进行同名像点匹配,结合相机的安装、成像参数及星历数据,可以用空间前方交会[2]的方法解算同名像点对应月面点的空间坐标。由于月球没有大气云层的覆盖,所以成像模型比较简单,由相机参数构建基于共线条件的严格几何模型[3],由立体像对直接解算地面点的空间坐标,可以达到比较高的定位精度。单轨前后视影像的同名点匹配方法见文献[4],当匹配了覆盖范围和密度足够的同名像点,并解算了同名点的空间坐标,经过三角构网[5]、网格扫描与插值[6]、灰度重采样[2]等步骤,就可以生成单轨数据对应的高精度规则格网DOM和DEM。
2 影像分块
要构建全月球三维影像,就必须把各单轨的DOM和DEM用一定的方式拼接起来。CE-2影像的数据量极大,一轨影像像素宽度为6144,高度为50~70多万行,数据量在3 GB以上,有前、后视两个线阵,覆盖全月面需要300轨以上的数据,只考虑原始影像就有TB级的数据量,处理过程中还会有各种中间数据。要将如此海量的数据有序地组织、管理并无缝拼接成整体,必须有稳定、可靠且可行的数据管理策略做支撑。由于计算机内存的限制,不可能一次性将两轨影像读入内存进行拼接,所以首先必须将单轨影像分割成小块,生成各小块对应的DOM和DEM,然后对各小块DOM和DEM作拼接处理,进而生成全月面三维影像。为了将单轨原始影像分割成变形极小、便于管理的小块,笔者引入了局部坐标系的概念。局部坐标系是用来管理地理数据的一个投影坐标系。地图投影就是将星球表面上以经纬度标识的点转换到平面直角坐标系的过程。传统的常用地图投影方式有墨卡托投影[7]、高斯-克吕格投影[8]等。墨卡托投影保证地图具有同形性,如google map采用的就是墨卡托投影[9],但其在极区附近的尺度变形极大,不适于全球影像的拼接。与这两类投影方式相比,本文将要介绍的局部坐标系构建简单,便于坐标转换及数据管理,基于局部坐标系对原始影像进行投影,所得影像在任意经纬度位置的变形都很小。下面讲述该坐标系的构建过程。
2.1 局部坐标系构建
本文全月球制图采用球形月固坐标系,参考椭球体为正球体,球形半径 R 为1 737 400.0 m。假设在一轨影像的F(前视)图和B(后视)图中匹配了一定密度的同名像点,并且解算了同名像点的空间坐标,现截取F图的一段影像以及该影像内的同名像点,设同名像点集为S。以S为数据源,构建流程如下:
(1) 将S中所有的点三角构网生成网格N。
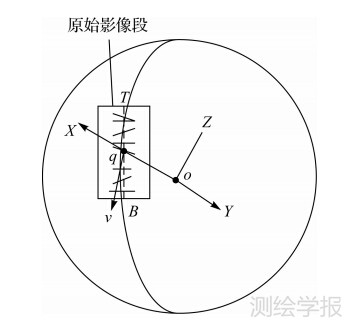
(2) 找出网格内所有通过图像纵向中间线(如图 1中的虚线TB所示)的三角形边,记为边表E。
(3) 确定E中每条边与图像中间线的交点,记为点集P。
(4) 在点集P中找出最为接近影像中心的点q。
(5) 记月固坐标系[10]的原点(月心)为o,如图 1所示,以oq作为局部坐标系的X轴方向;将P中的所有点根据其空间坐标拟合一条直线,记该直线方向为向量v;以oq×v所得向量方向作为Y轴方向,以X×Y作为Z轴方向,从而构建了以月心o为原点的右手局部坐标系。
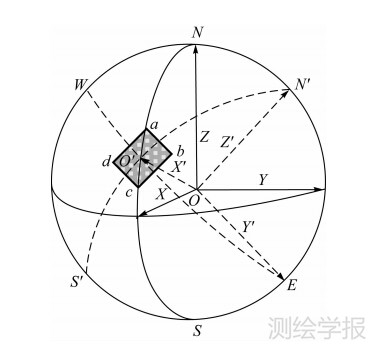
如图 2所示,o为月心,实线代表月固坐标系,虚线代表局部坐标系。 N′、S ′分别为局部坐标系下对应的北极和南极点,WE为赤道。矩形块abcd为局部影像块。O′为局部坐标系下,经纬度为0的位置。
|
| 图 1 局部坐标系构建示意图 Fig. 1 Sketch map of local coordinate system construction |
|
| 图 2 局部坐标系 Fig. 2 Local coordinate system |
此处需要说明两点:
(1) 以oq作为X轴方向可以保证q点(影像块中心点)处于局部球面坐标系零度经线与零度纬线的交点,这一特性保证了在作圆柱投影变换时只有很小的变形。
(2)CE-2是极轨卫星,由于月球自转的影响,卫星轨迹在月面的投影不是沿经线方向,而是从东南向西北方向偏,与经线成一定夹角,在赤道附近夹角最大(因为赤道的月表线速度最大)。通过将oq×v作为Y轴方向,可以保证局部球面坐标系的经线方向与卫星的飞行方向近似一致,从而在后续生成局部影像块时,可使局部影像块的纵向与原始影像纵向基本一致,使影像尽量充满局部影像块的矩形区域,而不至于出现过多的无数据区域,进而减小数据量,有利于后续的拼接处理。
从构建过程可知,局部坐标系是一个以月心为原点的空间三维直角坐标系,并且可以和月固坐标系相互转换。设局部坐标系三轴在月固坐标系中对应的单位向量为X、Y、Z,则由X、Y、Z按行排列构成的矩阵即为月固坐标系与局部坐标系间的转换矩阵。局部坐标系中点的空间坐标亦可用经纬度、高程表示,记为局部经纬度、高程。
设某点在局部坐标系下的坐标为Pl,月固坐标系下坐标为Pm,则有如下转换式
由于同名像点集 S 中任一点的月固经纬度、高程已知,所以其局部经纬度、高程可通过式(1),再做相应变换求得。局部坐标系类似于站心坐标系[11],但在细节上又有差异,主要表现在:
(1) 此处的局部坐标系坐标原点与月心重合,因此在作坐标转换时,只有旋转变换;月面任一点的高程h=x2+y2+z2-R,由于旋转变换不改变向量长度,因此转换到局部坐标系后的空间点,其高程与月固坐标系下的原始高程一致(均为从球心到表面点的连线长度),由此可知,局部坐标转换只改变 DOM、DEM的投影位置,而不改变其中的数据值。而在站心坐标系下,坐标原点为表面某点,同一点在不同的站心坐标系下有不同的高程,在与月固坐标系进行相互转换时,高程要重新计算,增加了计算量;若在生成局部DEM 时就以原始的月固高程进行插值,则每一点在站心坐标系下的z值仍然要保存,否则无法实现点坐标在站心坐标系与月固坐标系之间的相互转换,从而加大了数据存储量。
(2) 站心坐标系的X轴正向北,Y轴正向东,达不到使X轴方向与卫星飞行方向近似一致的效果。
2.2 生成局部影像块
通过截取原始影像及其同名点,可以构造该块对应的局部坐标系。将该影像块转到局部坐标系后,通过正轴圆柱投影(后面简称圆柱投影),可以生成其对应的局部影像块。下面介绍局部影像生成方法。 CE-2的分辨率约为7 m/像素 ,根据月球半径R可以换算出在月球赤道上每一角度对应的像素数,记为r,有:r=( π ×R)/(180×7)=4 331.8。为了保证局部影像与原始影像具有同样的空间分辨率,以1/r度(即每像素对应的角度,约为0.000 23 ° )作为局部影像块的像素尺寸,局部影像块的宽高可由同名点局部经纬坐标范围及像素尺寸确定。
对于局部影像块中任一像素点p(i,j),由以下步骤可以确定其灰度值。
(1) 首先计算p点对应的局部经纬度,计算公式如下
式中,L min 、B min 为同名点集中最小的局部经纬度值,将该位置定为局部影像块左下角。
(2) 根据p点的局部经纬度,确定p点位于网格内的对应三角形的索引k,其中,三角形顶点的局部经纬度、原始经纬度高程及原始影像坐标均已知。
(3) 根据三角形k的顶点及p点的局部经纬度,线性插值得到p点对应的原始影像像素坐标(i′,j′)及高程(局部高程和原始高程一致)。
(4) 根据(i′,j′),在原始影像中作一次灰度重采样即可得到p点的灰度值。
经过上述步骤,可以将位于三角网内的原始影像任一点映射到局部影像上,网格外的区域则直接丢弃,由步骤(3)得到的高程可以同时生成 DEM 。
根据上述局部影像的构建方法可知,局部影像像素坐标与局部经纬度可以相互转换,进一步可由局部经纬度转换为月固经纬度,因此可以从局部影像集中提取月球任一位置的影像。给定月球经纬度L、B,提取该位置的局部影像流程如下:
(1) 根据每轨影像的星历数据确定覆盖经度L的影像轨号N。
(2) 根据纬度B确定该纬度处的局部影像块号M。
(3) 从第N轨的局部影像集中取出第M块。
(4) 将L、B根据式(1)转换到局部经纬度L′、B′。
(5) 由L′、B′根据式(2)可以得到该位置对应的局部影像像素坐标。
(6) 根据像素坐标在局部影像块中作灰度重采样,即可得到该位置处对应的影像灰度值。
2.3 局部影像块变形分析
首先将原始影像转到局部坐标系,然后经圆柱投影生成局部影像,在此过程中,球面经纬线被拉伸展平为直线矩形网格,由圆柱投影的性质可知,投影后的影像沿经线方向没有变形,随纬度增加,纬线变形增大。
为了兼顾提高效率与减小变形的需要,一般在原始影像中取 1°纬度范围的影像数据来生成局部影像块,月固1°范围的纬度方向(经线方向)区域在局部坐标系中亦约为1°的范围(因 为局部影像与原始影像具有相同的像素分辨率)。在局部影像块中,其中心的局部经纬度近似为0,在图 2中,边ad和bc对应的纬度跨度为1 ° ,ab和dc边近似为0.5 ° 纬线,则在ab和dc边上,即圆柱投影在0.5°纬线上的相对变形为
绝对变形为
式中,w为原始影像宽度,为6144,故绝对变形大小为I abs =0.234像素。可见变形极小,近似可以忽略。并且该变形与原始影像所处的经纬度位置无关,而传统的投影变换变形大小与所处的经纬位置密切相关[12]。
图 3(a)是从嫦娥二号第401轨F视图截取的一段原始影像,其纬度范围是北纬61°—62°,图 3(b)是图 3(a)生成的局部影像块,图 3(b)边界的黑色区域是位于同名点网格外的部分,由于无法得到其原始影像坐标,故无数据。可以看到局部影像相对原始影像几乎没有变形,为下一步的影像拼接提供了良好的数据源。

|
| 图 3 原始影像与局部影像对比 Fig. 3 Comparison between origin and local image |
3 影像拼接
前面介绍了局部影像块的生成方法,下面介绍将各自独立的局部影像块拼接成一个整体的方法。首先建立一个全球影像框架,该框架对应一个全球投影坐标系,月球表面任一点经圆柱投影均可映射到框架内的某一像素位置,框架内任一点都有确定的全球经纬坐标。对于任一局部影像块,首先要确定与其相邻且有重叠的局部影像。
可以由局部影像块所对应的局部坐标系确定其所处的全球经纬度范围,并且只要两块影像的经纬度覆盖范围有重叠,即可确定为重叠影像。但CE-2的数据量非常大,如果从所有局部影像块中遍历查找经纬覆盖范围有重叠的块,时间开销将非常大。因此设计了一个全球经纬格网结构,每个网格区域对应一定范围的经纬跨度,在生成局部影像块时,根据每块的经纬覆盖范围,将其索引保存在覆盖该块的网格节点内。通过该结构,能以O(1)的时间复杂度[13]快速获取任一经纬范围内的所有局部影像块,记为影像集合 Is,Is中只包含了少量的影像块,因而能从Is 中快速确定有重叠的影像块。对于某经纬度范围内的一已知块,可能有一块或多块邻近轨的局部影像与其重叠,纬度越高,重叠越大。多块的遴选策略是:首先剔除影像质量差的重叠块;若其他块与已知块的重叠率均小于20%,则取重叠率最大的一块参与拼接;若有重叠率大于20%的块,则取大于20%的块中重叠率最小的一块参与拼接。这样的策略既保证了一定的重叠率,又减少了重叠块间的重复拼接。
3.1 影像配准
得到了邻接的影像块,需要对各影像进行配准,配准包括匹配重叠块同名点和坐标校正。同名像点匹配不是本文的重点,笔者采用SIFT[14, 15]和SURF[16, 17]算法提取影像特征;然后根据两个局部影像块四角的经纬度确定两重叠影像块的大致相对位置关系,以该位置关系为基础,在一个较小的范围内进行特征搜索、匹配。试验表明,这样的匹配策略可以达到很高的匹配效率、正确率和匹配精度。
3.1.1 偏移传递控制
如果直接一块一块地按序向全球影像框架中加入局部影像块,则后面加入的影像块要向前面已加入的影像进行配准。当加入若干轨的局部影像块后,发现后面加入的轨会向一个方向偏移,即新加入的影像在全图中的位置与其真实位置产生了一定偏差,如图 4所示,粗黑线框为加入的第1轨影像,虚线框为第2轨影像与第1轨影像进行同名点配准后的位置,细实线框为第2轨影像由立体像对解算空间坐标所确定的位置,即该轨的真实月面位置。
拼好的影像每一像素位置都对应月面经纬度,一方面,影像偏移就意味着其在月面的位置发生了移动,从而增大了影像定位的误差,这是不允许的;另一方面,研究的最终目的是由各单轨数据拼出覆盖全月面的DOM和DEM,若在拼接过程中任由这种偏移在影像块间向后扩散传递,将导致最后的影像不能合起来形成一个闭合的球面。

|
| 图 4 影像偏移示意图 Fig. 4 Sketch map of image shift |
产生这种现象的根本原因是:根据经纬度坐标生成局部图像块,以此为基础进行影像拼接。而由于卫星星历的误差和姿态的不稳定性[18],每轨F、B图解算的经纬度有随机和系统误差[19],从而导致将影像投影到月表时会产生定位误差,使不同轨的重叠影像不能很好地配准。当通过全局优化校正对多轨影像进行配准时,这种误差会在各轨间发生传递、累加,不断放大,以致最后不能合成一个球面,因此必须进行校正偏移传递的控制。
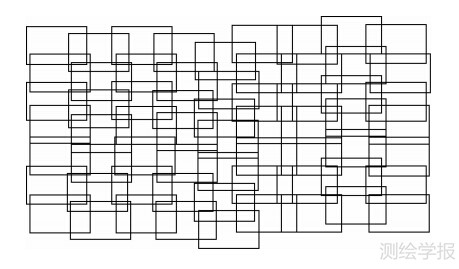
对于覆盖全球的局部影像块,按各块的邻接关系,顺序排列成一个影像格网,如图 5所示。取格网中m×m的子网,其中包含相邻的m×m块局部影像。将子网作为校正的单元,通过构造坐标校正模型,由相邻影像的同名点建立误差方程组,采用最小二乘方法求解方程组得到校正参数,进而对子网内各影像块坐标进行校正,从而使相邻影像能够无偏地配准。同时,将子网边界的影像块作为控制块,其坐标保持不变,保证了坐标校正只在子网内进行,校正偏移不会向其他子网传递;通过使相邻子网的边界重叠一行或一列,即相邻子网的邻接边界块是相同的影像块,而各边界影像块在校正时保持不变,从而保证了子网之间的数据连续性,使各子网之间无需校正即可自动配准。
以子网为校正单元可以缩小校正方程组的规模,子网不能太大,否则方程组规模过大而无法进行解算(内存限制),其次,太大的子网会增加影像的变形;子网也不能太小,否则达不到全局优化的效果。子网内影像块的数量,在中低纬区为m×m;在高纬区,由于影像重叠大,部分块会被剔除。
|
| 图 5 影像格网示意图 Fig. 5 Sketch map of image grid |
3.1.2 坐标校正
以重叠影像同名点为基础,采用一种在影像网格中进行全局优化的方法,对网格内各影像块的坐标进行校正,从而使子网内各相邻影像块达到最优的配准、吻合,同时保证坐标校正不在子网间传递。由于局部影像块是已进行了透视校正的正射影像,基本消除了透视变形,所以可近似认为重叠影像块之间只存在平移、旋转、缩放变换,用一次有理多项式模型即可近似地描述这种坐标变换关系[20]。下面介绍校正过程。
首先将子网中心(m/2,m/2)处的影像块对应的局部坐标系设为基准坐标系 C b。
对于子网内位于第i行、j列的影像块,记为 IMG (i,j),确定与其邻接的影像块,并匹配同名点,得到同名点集,记为P(i,j)。P中任一点在基准坐标系 C b中的局部经纬坐标可由式(1)、式(2)得到,计算方法为:
(1) 首先根据点在局部影像块中的像素坐标,由(2)式得到其局部经纬坐标。
(2) 由式(1)的逆变换可得该点的月固经纬坐标。
(3) 再由式(1)可得该点在 C b所确定的局部坐标系内的局部经纬坐标(L c i,j,B c i,j)。
(4) 由式(2)可将(L c i,j,B c i,j)转换为由 C b所确定的局部影像块内的像素坐标(x c i,j,y c i,j)。
全局优化的目标是:使所有重叠影像所匹配的全部同名点经坐标校正后的距离最小。目标函数为
式中,Ns,t为第s块与第t块匹配的同名点数量,若两块无重叠,则该值为0;a、b、c、d、e、f为各块待求的校正参数,x′、y′为校正后同名点在 C b所确定的局部影像块内的像素坐标。根据式(5)的优化目标,分内部和边界相邻影像块两种情况建立误差方程。
对于子网内部的非边界相邻影像块匹配点,此处以 IMG (i,j)、 IMG (i,j+1)为例,建立如式(6)的误差方程
式中,0
同时为了使相邻子网能够自动吻合,让相邻子网的边界重叠,即:对于左右相邻的子网,左子网的右边界影像块与右子网的左边界影像块是同一影像块。以子网左边界第i行的影像块为例,对应的误差方程为
在式(6)、(7)中,X c i,j、Y c i,j、X c i,j+1、Y c i,j+1为两影像块中同名像点的行列坐标向量,每个内部影像块都有6个待求解的校正系数a、b、c、d、e、f,可表达两相邻影像间的旋转、平移、缩放等仿射变换[20]。对于所有的相邻影像块同名像点集均可建立类似的误差方程。将整个m×m子网内所有的误差方程列在一起,共有6×(m-2)×(m-2)个未知数,只要每个影像块的独立同名点数超过6个,便可用最小二乘平差[21]方法求解,得到各影像块校正参数的全局最优解。
得到了校正参数后,用式(8)校正子网内部各影像块的像素点在基准坐标系中的坐标
表 1是解算一个10×10子网的校正参数后所得的相关数据,其中共匹配了13 242对同名点。
从表 1中数据可以看出,经过优化校正后,同名点的坐标偏差显著减小,使重叠影像相互之间更好地配准,从而能够有效减弱拼接后的模糊和重影。
3.2 灰度融合
影像进行配准之后,对于重叠影像必须进行灰度融合,采用如下的融合方法。假设有重叠的相邻影像块为I1和I2,两影像块中对应的重叠区域为A、B,其中A∈I1,B∈I2。融合后的影像为I,灰度融合式见式(9)
在式(9)中,v代表融合权重,根据像素点到I1中非重叠部分边界的距离d确定,如式(10)所示
当d增大时,v从1变小直至0,融合图像灰度也从I1向I2缓慢地平滑过渡,从而消除了拼接缝和灰度跳变。
图 6是用嫦娥二号第401至第410轨的北纬22—31°范围内的数据进行拼接所得的DOM和DEM,其中DEM用伪彩色图显示,红色表示高海拔,蓝色表示低海拔。由于各轨影像成像时刻不同,导致存在亮度差异,而笔者是在原始分辨率的影像上进行拼接,灰度过渡带的宽度D一般取几十至几百个像素,较局部影像块的宽度(大于6000)要小很多,所以在将拼接后的DOM缩小到图 6大小后,这种灰度过渡效果无法呈现,而各轨影像的亮度差异却显现出来,从而导致图 6中的DOM呈现瓦片状结构。根据文献[18]的结论,通过对各轨原始影像的每个像素都采用不同的光度校正参数进行逐一校正,可以基本消除这种现象,笔者暂未对原始影像作类似处理。该图采用切赤道的正圆柱投影方式进行显示,向上为北,向右为东,可见各轨影像在投影坐标系中呈右下到左上的分布,进一步说明了卫星轨迹在月面的投影与经线呈一定夹角。
图 7是将部分月面DOM与DEM叠加显示后的三维景观图,分辨率为7 m,从中可以清晰地看到月面地形的起伏。
4 结 论
本文提出了一种投影坐标系,该坐标系以若干已知空间坐标的图像点为基础来构造,通过对原始影像进行分块,并在各块所对应的局部坐标系内对其进行圆柱投影,相当于在赤道附近对原始影像投影,保证了生成的局部影像变形极小,并且变形大小与所处的月固经纬度位置无关。将单轨的月面影像分割成小块的局部影像块之后,可以方便地在微机上对海量的高分辨率月面影像进行拼接处理。通过建立影像子网,在匹配了重叠影像块同名点的基础上,采用基于全局优化的坐标校正方法,对各影像块坐标进行微调整,使重叠影像精确配准,并对校正偏移进行了有效的控制,保证其不会向后累加、传递。
试验结果表明,该拼接方法可以有效地自动处理嫦娥二号月面影像,并能达到很好的拼接效果;DEM数据亦可用类似的处理过程进行拼接,最终得到全景三维月图。此外,该拼接过程可以在多台微机上同步进行,亦可用多线程的方法实现更大程度的并行处理,从而大幅提高数据处理速度。
方程组残差均方值 同名点最小坐标偏差 同名点最大坐标偏差
校正前 12.306 1.2 51.8
校正后 5.237 0.1 23.4

图 6 拼接好的部分全图DOM和DEM
Fig. 6 Part of mosaicked DOM and DEM
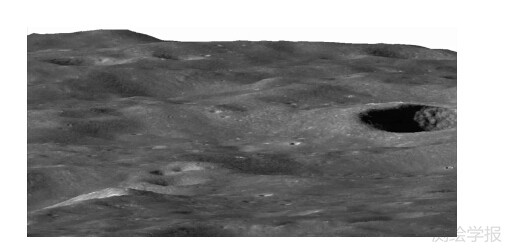
图 7 月面局部3维景观图
Fig. 7 The 3D landscape map of part of lunar surface
| [1] | HOFMAN O, NAV P. DPS-A Digital Photogrammetric System for Producing Digital Elevation Models and Ortho Photos by Means of Linear Array Scanner Imagery[J]. The International Archives of Photogrammetry and Remote Sensing, 1982, 24(3):216-227. |
| [2] | LI Deren, ZHOU Yueqin, JIN Weixian. The Outline of Photogrammetry and Remote sensing[M]. Beijing: Surveying and Mapping Press, 2001. (李德仁,周月琴,金为铣. 摄影测量与遥感概论[M].北京:测绘出版社,2001.) |
| [3] | YUAN Xiuxiao, YU Junpeng. Calibration of Constant Angular Error for High Resolution Remotely Sensed Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2008,37(1):36-41.(袁修孝,余俊鹏. 高分辨率卫星遥感影像的姿态角常差检校[J]. 测绘学报,2008,37(1):36-41.). |
| [4] | YANG Sheng, LI Xuejun, YANG Ahua, et al. Auto and Parallel Disposing of Feature Points Extracting and Matching of Orbits of Chang’E 2 Selenograph[C]// Proceedings of the 31st Chinese Control Conference. Hefei:[s.n.], 2012:5601-5606. |
| [5] | LI Xuejun, WANG Linxu, WU Yunhui, et al. A Fast TIN Generation Algorithm Based on Large-scale Unorganized Terrain Points[J]. Computer Simulation, 2009(11):211-214.(李学军,王林旭,吴涢晖,等.大规模地形散乱点的快速构网算法[J].计算机仿真,2009(11):211-214.). |
| [6] | HEARN D, BAKER M P. Computer Graphics with OpenGL,3rd ed. Edition[M]. London: Pearson Education, 2004. |
| [7] | REN Liucheng, YANG Xiaomei, ZHAO Zhongming. The Research on the Space Mercator Projection[J]. Acta Geodaetica et Cartographica Sinica,2003,32(1):78-81.(任留成,杨晓梅,赵忠明. 空间墨卡托投影研究[J]. 测绘学报, 2003,32(1):78-81.). |
| [8] | HU Yuju, GONG Jianwen. Map Projection[M]. Beijing: Publishing House of Surveying and Mapping, 1992.(胡毓钜,龚剑文. 地图投影[M]. 北京:测绘出版社,1992.) |
| [9] | CUI Jinhong, WANG Xu. Research on Google Map Algorithm and Implementation[J]. Computer Science, 2007,34(11):193-195.(崔金红,王旭. Google地图算法研究及实现[J]. 计算机科学, 2007,34(11):193-195.) . |
| [10] | XI Xiaoning. Orbit Design of Lunar Probe[M]. Beijing: Publishing House of National Defense Industry, 2001:12.(郗晓宁. 月球探测器轨道设计[M].北京:国防工业出版社,2001:12.) |
| [11] | NING Jinsheng, LIU Jingnan, CHEN Junyong, et al. Theory and Technology of Modern Geodesy[M]. Wuhan: Wuhan University Press,2006:188-189. (宁津生,刘经南,陈俊勇, 等. 现代大地测量理论与技术[M]. 武汉:武汉大学出版社,2006:188-189.) |
| [12] | REN Liucheng. Space Projection Theory and Its Application in Remote Sensing Technology[M]. Beijing: Science Press, 2003: 13-15.(任留成.空间投影理论基础及其在遥感技术中的应用[M].北京:科学出版社,2003:13-15.) |
| [13] | CORMEN T H, LEISERSON C E, RIVEST R L, et al. Introduction to Algorithms(Second Edition)[M]. Massachusetts: MIT Press, 2001:41-44. |
| [14] | LOWE D G. Object Recognition from Local Scale-invariant Features[C]//Proceedings of the International Conference on Computer Vision.Washington DC:[s.n.] , 1999(2): 1150-1157. |
| [15] | KE Y, SUKTHANKAR R. PCA-SIFT: A More Distinctive Representation for Local Image Descriptors[C]//Proceedings of IEEE Computer Vision and Pattern Recognition. Washington DC:[s.n.], 2004: 511-517. |
| [16] | LOWE D G. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2):91-110. |
| [17] | BAY H, ESS A, TUYTELAARS T, et al. Speeded-up Robust Features(SURF)[J]. Computer Vision and Image Understanding, 2008,110(3):346-359. |
| [18] | LI C L, LIU J J, REN X, et al. The Global Image of the Moon by the Chang’E-1: Data Processing and Lunar Cartography[J]. Science China Earth Sciences, 2010, 53(8): 1091-1102.. |
| [19] | YUAN Xiuxiao, YU Xiang. Calibration of Angular Systematic Errors for High Resolution Satellite Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2012,41(3):385-392.(袁修孝,余翔. 高分辨率卫星遥感影像姿态角系统误差检校[J]..测绘学报,2012,41(3):385-392.) . |
| [20] | JOHN R J. Introductory Digital Image Processing: A Remote Sensing Perspective[M]. London: Pearson Education, 2005:233-238. |
| [21] | TRIGGS B, MCLAUCHLAN P, HARTLEY R, et al. Bundle Adjustment——A Modern Synthesis[J]. Lecture Notes in Computer Science. 2000: 298-372. |