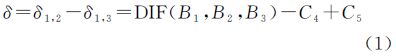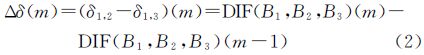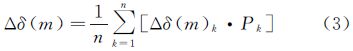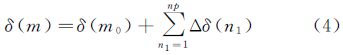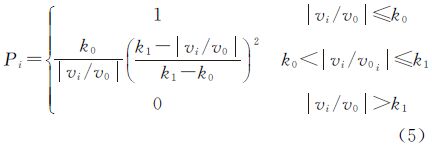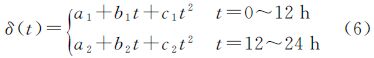2. 上海海洋大学 海洋科学学院,上海 201306
2. College of Marine Sciences,Shanghai Ocean University,Shanghai 201306,China
1 前 言
随着GNSS现代化进程的加快,观测信号已从单频、双频逐步向三频甚至多频发展。早期受实测数据的限制,大多有关三频信号组合定位[1, 2, 3]或模糊度确定[4, 5]等的讨论一般均基于模拟观测值进行。随着相关GNSS系统建设的不断推进,实测的三频信号开始逐步用于定位并得到初步研究[6, 7]。对实测数据分析的结果表明,QZSS系统三频信号频间偏差相对稳定[8],而GPS系统三频观测信号间存在显著的偏差、不一致性,且这一偏差是随时间变化的[9, 10, 11]。文献[9—11]提出了估计频间偏差的方法,分析了频间偏差的周期性及其产生原因,并且构造了函数模型。后者提出的方法更适用于实时、快速地处理大量观测数据。
基于双差观测的相对定位中,三频信号频间偏差可以完全抵消。然而,在采用非差观测的精密单点定位(precise point positioning,PPP)[12, 13, 14, 15]中,稳定的频间偏差会被非差模糊度参数所吸收,影响非差模糊度参数的特性[16, 17]。频间偏差随时间变化的部分则被卫星钟差所吸收,使得采用无电离层组合L1/L2(B1/B2)与L1/L5(B1/B3)估计的卫星钟差具有不一致性。采用常规方法进行卫星钟差服务时,需要求解两套钟差产品,会增加成本和计算负担。为了消除钟差产品的不一致性并提高效率,需要对三频信号频间钟差偏差(inter-frequency clock bias,IFCB)进行快速估计,并实现模型化。
随着我国BeiDou系统的逐渐完善,对应的服务将会逐步展开[18]。卫星IFCB变化的分析对其模型化及卫星钟稳定性的评估具有重要意义,而目前针对我国导航系统IFCB的估计及其特性研究尚未引起足够的关注。
2 卫星IFCB的抗差估计方法一般情况下,频间偏差采用非差观测模型来估计,解算参数包括模糊度和卫星频间偏差等。对应的公式为[9, 10, 11]
式中,δ为IFCB;δ1,2、δ1,3分别为采用B1/B2、B1/B3观测解算得到的卫星钟差;DIF(B1,B2,B3) 为两无电离层延迟组合(B1/B2、B1/B3)的差;C4、C5分别为无电离层延迟组合B1/B2、 B1/B3对应的模糊度。式(1)包括相位缠绕、卫星和接收机天线相位中心等。接收机对于频间偏差的贡献程度关系到IFCB的估计策略。当接收机的影响可以忽略时,可以直接采用式(1)进行IFCB的估计。否则,IFCB的估计与常规的卫星钟差估计方法一样,要进行基准的选择[12, 19]。为了提高解算速度和计算效率,满足实时服务的需要,本文IFCB的解算采用历元间差分法[12, 13, 14, 19, 20]。当接收机的影响可以忽略时,历元m 与 m-1进行差分得到 式中,△为历元间差分算子;△δ(m)为IFCB的历元间差值。假设有n个测站,则IFCB的历元间差值可以写为 式中,Pk为各测站历元间IFCB对应的权。在求得历元间IFCB的基础上,选择一参考历元,就可以进行基于参考历元的IFCB的计算,对应公式如下 式中,δ(m0)为m0历元的卫星IFCB;△δ(n1) 为第 n1历元的IFCB;np为解算历元距离参考历元的历元个数。为了减弱较大误差对解算结果的影响,数据处理过程中采用了抗差估计方法进行历元间IFCB的解算。所采用的权函数[21, 22]为
式中,Pi为观测值的权;vi为残差;v0为方差因子;k0、k1为常数,按照文献[21],本文分别选k0、k1为1.5、3.0。 3 实测数据处理与分析为了分析BeiDou系统IFCB的特性,同时验证本文提出的估计方法,对2012年1月的观测数据进行了解算,数据采样率为30s。由于观测站的分布问题,本文主要进行GEO卫星(G01、G03、G04)经验模型、日变化等的分析。数据处理中,初始权取为1。
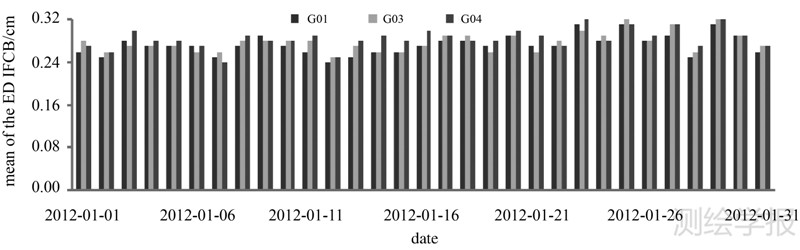
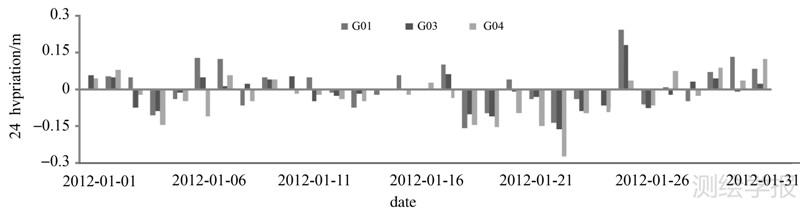
3.1 IFCB变化卫星IFCB的变化对分析卫星钟稳定性及采用DIF(B1,B2,B3) 观测进行周跳探测[6, 7, 23, 24, 25]具有重要意义。这里分别给出IFCB的30s和24h变化量。图 1为卫星G01、G03、G04的IFCB的30s平均变化量,图 2为24h变化量。
|
| 图 1 IFCB的30s变化量 Fig. 1 The variation of IFCB of 30 second |
|
| 图 2 IFCB的24h变化量 Fig. 2 24h variation of IFCB |
图 1表明30s GEO卫星IFCB变化量约为0.3cm,远远小于某一信号发生周跳时DIF(B1,B2,B3) 观测的变化量。因此,可以认为IFCB存在系统变化,但是这种变化不会影响采用观测DIF(B1,B2,B3)进行周跳探测。与GPS系统的IFCB 30s变化量[10]相比,两者处于一个量级。图 2表明BeiDou系统GEO IFCB日变化量大多在厘米级,只有少数达到了分米级。
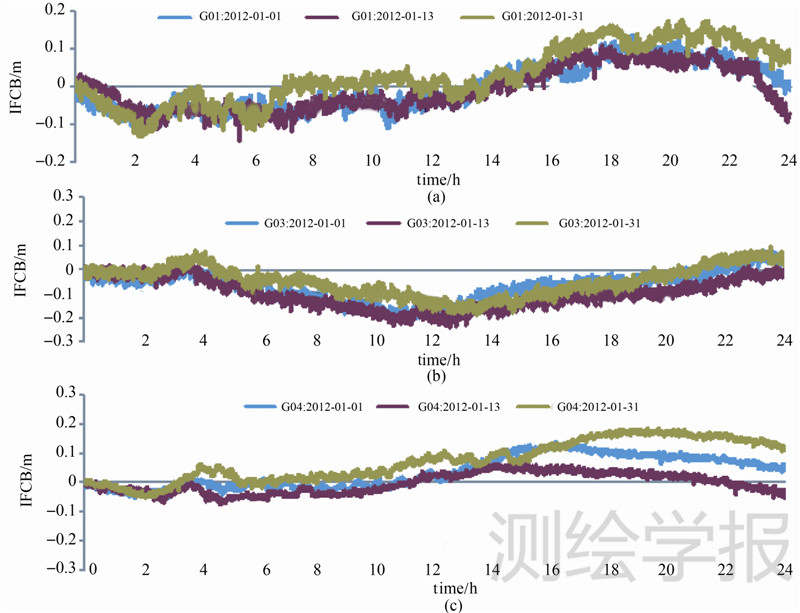
3.2 基于参考历元的 IFCB及其模型化在估计得到IFCB的历元间差值之后,采用式(4)就可以进行基于参考历元的IFCB的计算。为了分析IFCB的特征,本文选取每天的零时刻(BeiDou时)为参考历元进行计算。图 3(a)、(b)、(c)分别为G01、G03、G04 3颗卫星基于参考历元的IFCB结果。鉴于篇幅,本文只列出了1月1日、13日、31日的图示结果。
|
| 图 3 基于参考历元的IFCBs Fig. 3 Reference epoch based IFCBs |
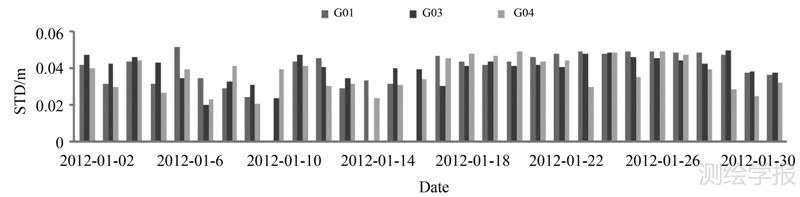
从图 3(a)-(c)来看,不同GEO卫星IFCB变化范围为-0.3~0.3m。3颗卫星的IFCB变化范围不完全一致,但都具有二次曲线的变化特性,且在当天第12h后振幅变大。为了研究IFCB的周期性,统计了2012-01-01 IFCB与剩余日期IFCB差值的STD(standard deviation),如图 4所示。
|
| 图 4 偏差对应的标准方差 Fig. 4 STD of the difference |
综合图 3和图 4,BeiDou系统IFCB也存在一定的相似性,即具有24h周期变化性。采用快速估计方法解算得到的IFCB,同样具有较高的精度。在非差PPP定位中,参考历元的IFCB会被模糊度参数所吸收,不影响定位的精度。根据GEO卫星IFCB的特征,本文采用二次分段函数进行IFCB的描述。对应函数如下
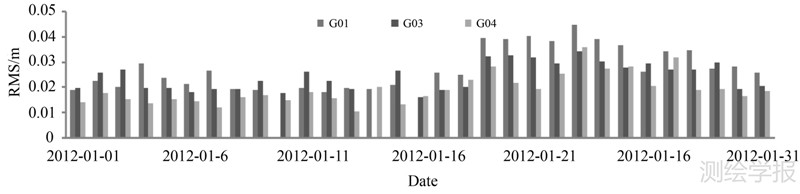
式中,a1、a2为常数项;b1、b2为线性项;c1、c2 为二次项;t为时间。利用最小二乘拟合得到模型参数估计值,将其与估计结果相比较得到偏差的RMS值,如图 5所示。
|
| 图 5 模型值与解算结果差异 Fig. 5 RMS of the difference between the modeled and estimated results |
图 5结果表明二次分段模型的改正效果大部分优于3 cm。采用该模型时,对于G01卫星IFCB的改正效果较差,对于GO4卫星的改正效果最优。统计各结果RMS表明,模型的平均改正率优于71%。
4 结 论本文采用实测的BeiDou数据详细分析了卫星IFCB的变化特性并对其进行建模,得到如下结论:
(1) 与GPS系统中Block IIF卫星类似,BeiDou系统三频信号也存在明显的IFCB,两者几乎在一个量级,大致在分米级。
(2) 从不同时间段GEO卫星的IFCB来看,IFCB的变化趋势大致相似,且具有二次曲线的特征和周期性。若采用分段的二次函数进行GEO卫星IFCB模型化,能达到平均71%以上的改正效果。
(3) BeiDou系统三频信号IFCB 30s的变化在毫米级,不会影响DIF(B1,B2,B3) 组合进行周跳探测。
文中所提算法及函数模型已应用于自主研发的软件中,实现了对BeiDou、GPS系统三频信号IFCB近实时的监测、分析。但从目前论述的IFCB产生的因素[9, 11]来看,本文提出的BeiDou系统GEO卫星IFCB模型尚不能完全反映其变化特性,因此需要更加深入地分析、研究我国导航系统三频信号不一致性产生的原因,以便对其进行更高精度的模型化。
| [1] | HATCH R. A New Three-frequency, Geometry-free Technique for Ambiguity Resolution [C]//Proceedings of ION GNSS. Fort Worth:[s.n.],2006:309-316. |
| [2] | ODIJK D. Ionosphere-free Phase Combinations for Modernized GPS [J].Journal of Surveying Engineering,2003, 129(4):165-173. |
| [3] | COCARD M, BOURGON S, KAMALI O, et al. A Systematic Investigation of Optimal Carrier-phase Combinations for Modernized Triple-frequency GPS [J]. Journal of Geodesy, 2008, 82(9): 555- 564. |
| [4] | LI B, FENG Y, SHEN Y. Three Carrier Ambiguity Resolution: Distance-independent Performance Demonstrated Using Semi-generated Triple Frequency GPS Signals [J]. GPS Solutions, 2010, 14: 177-184. |
| [5] | FENG Y, LI B. Wide Area Real Time Kinematic Decimetre Positioning with Multiple Carrier GNSS Signals [J]. Science China, 2010, 53(5):731-749. |
| [6] | LI Jinlong, YANG Yuanxi, XU Junyi, et al. Real-time Cycle-slip Detection and Repair Based on Code-phase Combinations for GNSS Triple-frequency Un-differenced Observations [J]. Acta Geodaetica et Cartographica Sinica, 2012,41(5):763-768.(李金龙,杨元喜,徐君毅,等. 基于伪距相位组合实时探测与修复GNSS三频非差观测数据周跳[J]. 测绘学报, 2011, 40(6):717-722.) |
| [7] | HUANG Lingyong,SONG Lijie,WANG Yan,et al. BeiDou Triple-frequency Geometry-free Phase Combination for Cycle-slip Detection and Correction [J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5):763-768.(黄令勇,宋力杰,王琰,等. 北斗三频无几何相位组合周跳探测与修复[J]. 测绘学报, 2012, 41(5):763-768.) |
| [8] | HAUSCHILD A, STEIGENBERGER P, RODRIGUEZ-SOLANO C. Signal, Orbit and Attitude Analysis of Japan’s First QZSS Satellite Michibiki [J]. GPS Solutions, 2011, 15(7):127-133. |
| [9] | MONTENBRUCK O, HUGENTOBLER U, DACH R, et al. Apparent Clock Variations of the Block IIF-1 (SVN62) GPS Satellite [J]. GPS Solutions, 2012,16(2):303-313. |
| [10] | LI H, ZHOU X, WU B,et al. Estimation of the Inter-frequency Clock Bias for the Satellites of PRN25 and PRN01 [J]. Science China Physics, Mechanics & Astronomy,2012, 55(11):2186 -2193. |
| [11] | LI H, ZHOU X,WU B. Fast Estimation and Analysis of the Inter-frequency Clock Bias for Block IIF Satellites[J].GPS Solutions, 2013,17(3):347-355. |
| [12] | LI H, CHEN J, WANG J, et al. Network Based Real-time Precise Point Positioning [J]. Advances in Space Research, 2010, 46(9):1218-1224. |
| [13] | LI H, CHEN J, WANG J, et al. Satellite-and Epoch Differenced Precise Point Positioning Based on Regional Augmentation Network [J]. Sensors,2012,12(6):7518-7528. |
| [14] | LI Haojun, WANG Jiexian, CHEN Junping, et al. The Realization and Analysis of GNSS Network Based Real-time Precise Point Positioning [J]. Chinese Journal of Geophysics, 2010, 53(6): 1302-1307.(李浩军,王解先,陈俊平,等.基于GNSS网络的实时精密单点定位及精度分析 [J].地球物理学报,2010,53(6):1302-1307.) |
| [15] | ZHANG Xiaohong, LI Xingxing, GUO Fei, et al. Server-based Real-time Precise Point Positioning and Its Application [J]. Chinese Journal of Geophysics, 2010,53(6):1308-1314.(张小红, 李星星, 郭斐,等. 基于服务系统的实时精密单点定位技术及应用研究 [J]. 地球物理学报,2010,53(6):1308-1314.) |
| [16] | BLEWITT G. Carrier Phase Ambiguity Resolution for the Global Positioning System Applied to Geodetic Baselines up to 2000km[J]. Journal of Geophysical Research, 1989, 94(8):10187-10203. |
| [17] | GE M, GENDT G, ROTHACHER M, et al. Resolution of GPS Carrier-phase Ambiguities in Precise Point Positioning (PPP) with Daily Observations [J]. Journal of Geodesy, 2008, 82(7):389-399. |
| [18] | YANG Yuanxi,LI Jinlong,TANG Jing,et al. Contribution of the Compass Satellite Navigation System to Global PNT Users[J]. Chinese Science Bulletin, 2011, 56(21):1734-1740.(杨元喜,李金龙,汤静,等. 中国北斗卫星导航系统对全球PNT 用户的贡献[J]. 科学通报,2011, 56(21):1734-1740.) |
| [19] | LI Haojun,WANG Jiexian,WANG Hu, et al. Precise Clock Error Estimation of GPS Satellite and Analysis Based on GNSS Network [J]. Geomatics and Information Science of Wuhan University, 2010,35(8):1001-1003.(李浩军,王解先,王虎,等.基于GNSS网络的卫星精密钟差估计及结果分析 [J].武汉大学学报:信息科学版, 2010,35(8):1001-1003.) |
| [20] | GE M, CHEN J, DOUSA J, et al. A Computationally Efficient Approach for Estimating High-rate Satellite Clock Corrections in Realtime [J].GPS Solutions.2011,15(2):9-17. |
| [21] | YANG Y. Robust Estimation of Geodetic Datum Transformation [J]. Journal of Geodesy, 1999, 73:268-264. |
| [22] | YANG Yuanxi, SONG Lijie,XU Tianhe. Robust Parameter Estimation for Geodetic Correlated Observations [J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(2): 95-99.(杨元喜, 宋力杰, 徐天河. 大地测量相关观测抗差估计理论[J].测绘学报,2002,31(2):95-99.) |
| [23] | LACY M, REGUZZONI M, SANSO’ F. Real-time Cycle Slip Detection in Triple-frequency GNSS [J]. GPS Solutions, 2012,16(5):353-362. |
| [24] | WU Y, JIN S, WANG Z, et al. Cycle Slip Detection Using Multi-frequency GPS Carrier Phase Observations: A Simulation Study [J].Advances in Space Research,2010, 46(2):144-149. |
| [25] | HE Haibo,YANG Yuanxi. Detection of Successive Cycle Slips for GPS Kinematic Positioning [J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(3):199-204.(何海波,杨元喜. GPS动态测量连续周跳检验 [J]. 测绘学报,1999, 28(3): 199-204.) |