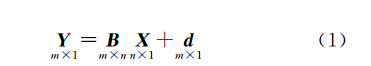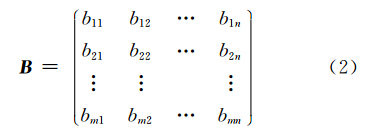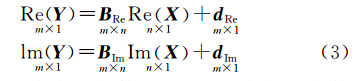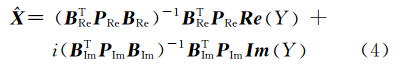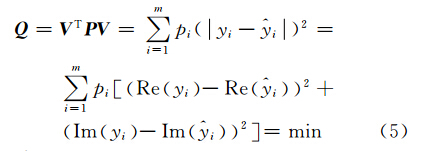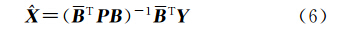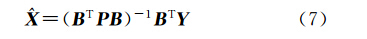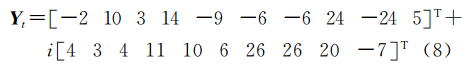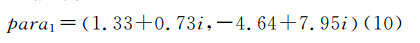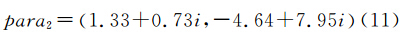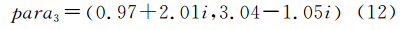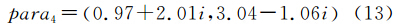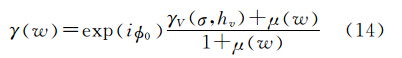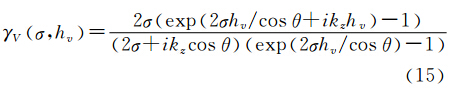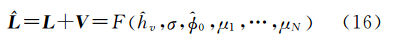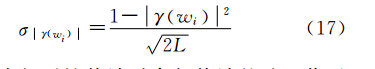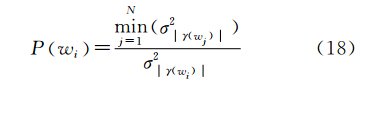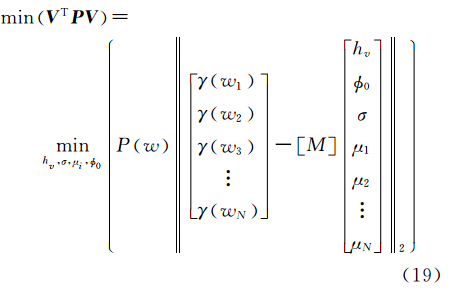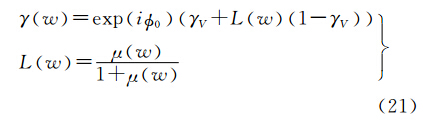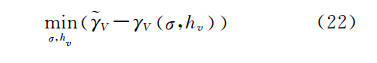1 引 言
传统的测量工作主要是在现实的实数空间中展开的,各种观测值及待估参数都是实数值,因此目前平差函数模型和随机模型以及相应的平差理论和方法都是建立在实数空间内。随着科学技术的发展,数据获取方式的多样化和现代化,近年来测绘及相关领域出现了一些以复数形式表达的观测数据,比如极化干涉合成孔径雷达(polarimetric SAR interferometry,PolInSAR)地表参数反演和植被高度估计[1, 2, 3, 4, 5],核磁共振图像(MRI)的边缘检测[6],地震传感器的相对和绝对定位[7],通信信号处理[8, 9],多源遥感图像融合[10],GNSS数据处理[11]、汛期降水预报等方面[12]。与实数数据一样,这些复数数据同样面临着如何从带有误差的观测值中找出未知量的最佳估计值的问题。经典的测量平差目前主要是以高斯提出的最小二乘准则作为平差准则,即以观测残差V的平方和最小作为确定最佳参数的估计准则,但目前涉及复数观测的数据处理时,主要还是依据观测过程,分步或直接解算,不能考虑观测误差、多余观测信息等。因此,本文考虑将实数域平差准则推广到复数域,介绍复数域中数据处理的最小二乘方法。首先总结一下目前数学领域中针对复数域数据处理的两种平差准则[12, 13, 14]和参数估计的数学表达式,然后采用数值算例定量对比了两种准则的优劣性。
为了进一步说明和推广复数最小二乘在测绘相关领域中的应用,本文将其应用到复相干性极化干涉 SAR植被高反演当中。PolInSAR技术综合了InSAR 对散射体高度敏感的特性,同时继承了极化信息对散射体结构敏感的优点[15, 16, 17, 18, 19],已经广泛应用于森林植被高度反演。根据植被高反演观测值为复数且存在多余观测的特点,将复数域最小二乘准则引入到植被高反演当中,根据观测值先验统计信息定权,建立平差函数模型和随机模型,构建一种复数最小二乘算法反演植被高度。该算法表达直观,易于编程实现。为验证算法有效性,本文利用极化干涉数据采用复数域最小二乘算法反演植被高,且与其他常用的两种植被高反演算法比较,并对其反演结果作了定性和定量评价。
2 复数域最小二乘
对于复数域线性系统,其函数模型一般可以表示为
式中,Y=[y1 y2 … ym] T 表示复观测向量;X=[x1 x2 … xn] T 表示复未知参数向量;d=[d1 d2 … dm] T 表示复误差向量;观测值数量m多于未知数个数n;B为复系数矩阵,它的每个元素都为复数
上述模型的基本形式和实数域最小二乘相同,不同点在于式中的每个元素都是复数。对于这样的复数域平差问题,目前数学领域有两种方法来进行处理:
(1) 第1种方法是以复数观测值残差的实部和虚部的平方和分别最小作为平差准则[12, 13]。即将观测方程分解为实部和虚部,利用传统的最小二乘分别求解未知参数的实部和虚部,然后合并参数实部和虚部的估计值从而得到最终的未知参数的估计值。下式即为分解后的观测方程
式中, Re 为取复数实部算子; Im 为取复数虚部算子。假设P Re 为观测值实部的权,P Im 为观测值虚部的权。此时,这样一个复数域平差问题就转换成两个实数域平差问题,然后利用经典的实数域最小二乘准则,可以得到参数的最小二乘解为
(2) 第2种方法是以复数观测值残差的模的平方和最小作为平差准则[12, 13, 14]。由于数学上模的平方等于实部的平方加上虚部的平方,故模的平方和最小意味着要保证复数观测值的实部残差平方和和虚部残差平方和的总和最小。这种准则同时兼顾了观测值的实部和虚部的误差,其表达式为
式中,=[1 2 … m] T 表示平差后的复观测向量;P表示观测值的权阵。经过推导[12, 13, 14],可得到复数线性最小二乘的解为
式中,表示B的共轭。式(6)即为复数域最小二乘准则下的法方程。当Y、X、d的元素值均为实数时,此时应用实数域经典平差理论,可得到实数域最小二乘准则下的法方程为
由上述两式对比可以发现,复数域最小二乘平差的结果与实数域最小二乘的结果在形式上基本相同,区别在于复数域的系数矩阵上多了个共轭。
值得注意的是,上述参数估计值均是针对复数线性系统参数求解问题,并基于不同平差准则通过构建法方程求解而得到的,本文称这种解算参数的方法为直接解法。然而,在测量及相关领域中涉及复数观测时非线性模型比较多。传统的方法是将数学模型进行线性化近似,略去高次项,从而将非线性问题化作线性问题来求解,然后基于上述两种准则求解未知参数。但是,当观测模型显式表达式十分复杂时,线性化比较困难,即使强行采取线性化近似,往往也会带来较大的模型误差,可能导致参数估计结果扭曲[20],故此时应采用非线性最小二乘迭代法求解,在解空间内逐一搜索迭代,直到找到满足代价函数最小的那一组解,即为最小二乘准则下的最佳估值。这种解算方法本文称之为迭代解法。至于具体采取哪一种解算方法,要根据观测模型的复杂度来灵活选择。
3 复数域平差准则对比
为了对比两种平差准则应用于复数域平差问题的优劣性,本文首先采用一个简单例子来说明。为了获取真值进行有效对比,本文利用复数域线性模型Y=aX+b构造算例。在构造时取复自变量X=1327219153-2 T +i·[3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21] T ,设未知参数的真值para=[ab] T =[1+2i3-i] T ,由此可得Y的真值Yt为
为了模拟观测值的随机噪声,本文在Yt的实部和虚部分别加上一个均值为0、方差为1的一维高斯噪声,从而构成了带误差的复数观测值Y为
假定观测值同等精度,即权阵为单位矩阵。接着,分别采用上面提到的两种平差准则和两种解算方法去求解。当采用残差的实部和虚部的平方和分别最小的平差准则(4)和直接解法时,可得para的估计值
基于准则式(4)采用迭代解法时,可得para的估计值
采用残差的模的平方和最小的平差准则式(5)和直接解法可得para的估计值
基于准则式(5)采用迭代解法可得para的估计值
表 1给出了两种准则分别应用直接解法和迭代法求得的参数统计指标对比。
| 平差准则 | 解算方法 | Y 的中误差 | Y 的均方根误差 | 残差的实部和虚部的平方和分别最小 |
| 直接解法 | 12.47 | 10.96 | |
| 迭代解法 | 12.47 | 10.96 | |
| 残差的模的平方和最小 | |||
| 直接解法 | 1.31 | 0.25 | |
| 迭代解法 | 1.31 | 0.25 |
由上述算例的参数估计结果以及统计指标对比结果中可以很直观地看出:① 对于复数域数据平差问题,采用残差的模的平方和最小的准则得到的参数估计值,相比采用残差的实部和虚部的平方和分别最小的平差准则得到的参数估计值更为准确,观测值的标准差和均方根误差更小;② 对于复数域线性系统,直接解法和迭代解法得到的参数估计值相同。
4 PolInSAR植被高反演的复数最小二乘算法
目前PolInSAR植被高反演算法主要有:① 三阶段算法[5];② DEM差分算法[19];③ ESPRIT超分辨率算法[17, 18];④ 六维非线性最优参数估计算法[4]。在这几类算法中,前3种算法不属于基于散射模型的直接参数解算方法,过程繁琐,不易理解和编程实现,且不考虑观测误差,无法给观测值定权从而评定精度。最后一种算法是一种直接参数解算方法,虽然易于理解,却没有考虑观测值的先验统计信息。此外,4种方法都没有考虑多极化观测提供的多余观测信息。针对这些问题,本文提出用复数最小二乘来进行PolInSAR植被高反演。下面首先根据物理模型和先验统计信息建立植被高反演的函数模型和随机模型,然后构建复数最小二乘算法估计植被高度。
4.1 复数最小二乘植被高反演算法
4.1.1 复数最小二乘植被高反演算法的函数模型
根据极化干涉SAR理论,在进行距离向频谱滤波消除基线几何去相干后的任意极化的复相干性可以表示为[3, 4, 5]
式中,w为单位复数矢量,对应于某一种极化方式; 0代表植被下的地表相位;hv代表植被高度;μw为地体幅度比;γV表示只由植被层产生的纯体相干性,其一般表达式为
式中,σ为消光系数,用于描述植被层散射体对入射波的吸收和散射过程;kz表示有效垂直波数,依赖于雷达波长λ和成像几何(垂直基线B⊥,入射角θ和斜距R)。式(14)就是 PolInSAR植被高反演的物理模型,即随机地体二层相干散射模型(random volume over ground,RVOG)。
从测量平差角度来看,该模型可以看做是以多极化复相干性为观测量,以植被高,消光系数等植被参数作为未知数的观测方程。故可以将观测方程作为平差的函数模型,将植被高求解看成是一个间接平差问题,则植被高平差求解的函数模型可以表示为
式中,L表示复观测向量;V表示改正数向量;F表示函数关系(14);^表示平差符号。当具备一定观测数量(N>3时)时,则可以采用复数域最小二乘求解。
4.1.2复数最小二乘植被高反演算法的随机模型
为了获取更为准确的参数估计值,本文这里考虑根据观测值的先验统计信息定权,从而得到测量平差所需要的随机模型。根据极化 SAR 理论,不同极化的复相干性的模的中误差表达式如下[21]
式中,L代表相干性估计时参与估计的独立像元样本总个数。在本文的植被高反演平差策略中,假定不同极化观测值之间互相独立。根据权的定义,本文选取中误差最小的那一组极化通道的复相干性作为单位权观测值,则可以得到任意极化通道观测值的权为
N代表参与平差的复相干性个数。式(17)即为的复数域最小二乘算法的随机模型。
4.1.3 复数最小二乘植被高反演算法的平差策略
在建立了复数最小二乘植被高反演算法的函数模型和随机模型模型后,接着就需要根据现有复数观测值和平差准则估计植被参数。对于单基线全极化干涉观测模式反演植被参数的情况,用户在拿到数据时,观测值只有3个线性极化通道 HH、HV、VV(根据单站互易性原理HV=VH )的复相干性γ HH 、γ HV 、γ VV ,没有多余观测。然而,根据电磁波极化合成理论,极化空间的任意极化通道的 SAR信号都可以由3个线性极化通道的信号线性组合获取[2]。因此,可以通过增加极化通道数量来增加复相干性的数量。由于RVOG 模型中植被散射体各向同性的假设,所有的消光系数不依赖于极化通道,因此每增加一个极化通道的复相干性,实数观测值数量增加两个,未知数(即与极化相关的地体幅度比μ)增加一个,存在多余观测。因此,本文从测量平差的角度出发,将这一问题看做一个复数域平差问题,利用建立的函数模型和随机模型,并选取残差模的平方和最小这一更优的平差准则构建复数最小二乘算法进行植被参数求解。由于观测模型为非线性模型,且模型的显式表达式十分复杂,线性化过程困难,因此本文选用迭代法求解。具体地,假定选取的极化通道数为N,则 PolInSAR 植被高反演的复数最小二乘准则表达式为
式中,[M]表示观测模型(14)。虽然增加极化通道观测值可以提高多余观测量,但同时未知数(地体幅度比μ )的个数也增加了,这样会使得参数求解更为复杂,因此极化通道个数选择不宜太多。同时为了改善平差中的病态问题,应当尽量选择相关性小的极化通道,因此极化通道选取时要兼顾参数反演的复杂性和稳健性。针对这一问题,本文在利用复数域最小二乘反演植被高时,选取了PD(phase diversity)相干最优化极化方式和Pauli基极化方式共5个极化方式,即PDHigh、PDLow、HV、HH+VV、HH-VV,此时观测量个数有10个,未知数个数为8个,存在2个多余观测量。
4.2 植被高反演质量对比方法
为了了解复数最小二乘算法反演性能,本文采取两种常用的PolInSAR植被高反演算法进行反演质量对比,即DEM差分算法和三阶段算法。
4.2.1 DEM差分算法
DEM差分算法的基本思想是利用两种相位中心高度分别接近于树冠和树底的极化方式的复相干性γwV和γwS。假设γwV对应的地体幅度比μwV为0,代入到 RVOG 模型可以求得地表相位的估计值0,将接近于树冠的γwV与地表相位0的相位差作为植被高对应的干涉相位,最后根据相位高程转换关系将相位差转换为植被高V。具体算法表达式如下[19]
根据物理先验信息,对于植被覆盖区域场景,一般可以认为 HV极化对应着冠层内的体散射机制,其散射中心接近于冠层,HH-VV极化对应着地面和树干作用引起二面角散射机制,其散射中心接近于地表[22]。故本文中的DEM差分法反演植被高时,选取HV和HH-VV 两种极化方式的复相干性对应式(20)中的γwV和γwS。
4.2.2 三阶段算法
三阶段算法是由文献[5]提出的一种基于 RVOG模型的植被高反演几何方法,它包括直线拟合、地表相位估计和植被高估计三个阶段,其提取的植被高精度较高,是目前PolInSAR反演植被高最常用的方法。具体地,该方法首先将RVOG模型改写成如下线性模型
由这个线性模型可知,复数观测值在复平面理论上呈直线分布。该方法首先利用一定数量的极化观测值通过直线拟合可以得到地表相位 0,然后假设 HV 极化方式地体幅度比为0,即μ HV =0,从而可以求得纯体相干性估计值V,接着建立二维查找表,找出差异最小的那一组值,从而求得植被高度hv,相应的约束条件如下
5 试验结果及分析
5.1 数据介绍
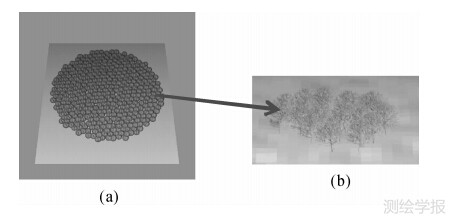
由于获取森林地区的植被高的实测资料比较困难,故本文采用欧空局发布的极化SAR数据处理软件PolSARpro中的森林模拟器模块模拟L波段全极化干涉数据来验证算法的优越性。表 2为模拟数据参数表,图 1为模拟的植被场景图和落叶林模型[23]。
|
| 图 1 模拟的植被场景图(a)和落叶林模型(b) Fig. 1 The simulated forest scene(a) and deciduous forest model(b) |
| 平台高度/m | 中心频率/GHz | 入射角 | 垂直基线/m | 水平基线/m | 方位向分辨率/m | 斜距向分辨率 | 植被类型 | 植被高度/m |
| 3 674.235 | 1.3 | 30° | -6.1 | 10.6 | 1 | 0.5 m | 落叶林 | 10 |
在图 1中,中间圆形区域为植被覆盖区域,其他区域为地面。图 2为场景对应的L波段极化干涉数据主影像对的HH、HV、VV 3个极化通道的功率图及总功率图。

|
| 图 2 L波段数据HH功率图(a)、HV功率图(b)、VV功率图(c) Fig. 2 L-band data power diagrams corresponding to HH(a),HV(b),VV(c) |
5.2 植被高反演结果及分析
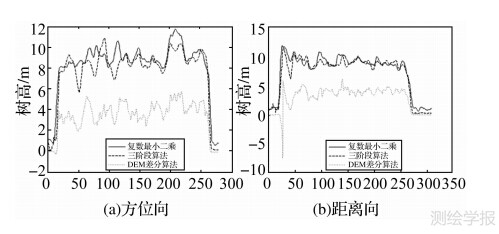
图 3所示的是本文提到的3种植被高反演算法得到的植被高剖面对比图。其中,图 3(a)表示的是图 2(b)中标注的横向剖面线(距离向)的植被高结果对比;图 3(b)表示的是图 2(b)中标注的纵向剖面线(方位向)的植被高结果对比。图 4为图 2(c)矩形方框区域内的植被高结果统计直方图。从这些结果可以直观地看出:① 3种方法反演的植被高在两个方向的整体趋势基本相同;② 复数域平差法反演的植被高度略高于3阶段算法结果,明显高于DEM差分法结果;③ DEM差分算法反演结果在距离向剖面出现部分负值。分析其原因主要是因为雷达观测模式使得该像元内散射机制在高度向分界不清晰,导致相干性估计获取的HV和HH-VV两种极化方式的相位中心相对位置与事先假定的相反。
|
| 图 3 L波段极化干涉数据植被高反演结果 Fig. 3 Tree height estimation based on L-band PolInSAR data |
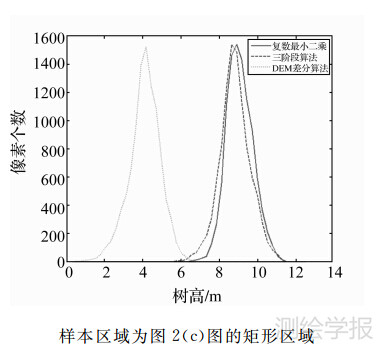
为了定量评价两种算法的性能,表 3给出了3种算法的统计指标比较,比较样本数为10000。从统计结果看,复数最小二乘算法得到的植被高平均值为9.17m,三阶段算法为8.92m,DEM差分算法出现了较严重的低估现象,均值仅为4.18m。相比10m的植被高理论值,本文中的复数最小二乘算法提取的植被高结果更为准确,其反演精度明显优于DEM差分算法,略优于三阶段算法。从反演模型和具体实现过程来分析,3种方法都是基于RVOG模型,但是采取的策略各不相同。DEM差分算法利用两个复相干性观测值采用类似三阶段法中直线拟合思想估计地表相位,但由于最后计算树高时模型简单,导致反演精度不高。三阶段算法虽然反演精度较高,但整个过程繁琐,不易理解和编程实现,且无法给观测值定权从而评定精度。相比而言,复数平差算法则具有表达直观、编程简单、能进行精度评定的等优点,且反演结果更为可靠。
|
| 图 4 两种方法得到的植被高结果统计直方图 Fig. 4 Histograms of tree height results corresponding to two methods |
| 植被高反演方法 | 植被高真值 | 植被高均值 | 平均误差 | 均方根误差 |
| DEM差分算法 | 10 | 4.17 | 5.82 | 5.88 |
| 三阶段算法 | 10 | 8.92 | 1.15 | 1.34 |
| 复数最小二乘 | 10 | 9.17 | 0.91 | 1.07 |
本文针对复数域测量数据处理问题,把实数域最小二乘准则推广到复数域,研究结果表明:
(1) 对于目前复数域数据处理时常用的两种平差准则,采用残差的模的平方和最小的平差准则得到的参数估计结果比采用采用残差的实部和虚部的平方和分别最小的平差准则得到的参数估计值更为准确,精度更高。
(2) 采用复数域最小二乘的方法来处理极化干涉SAR植被高反演所得的植被高精度高,明显优于DEM差分算法的精度,略优于三阶段算法的精度,并且复数域最小二乘计算还具有表达直观、编程简单、能进行精度评定的等优点。
(3) 对于PolInSAR植被高反演的复数域最小二乘,观测值按式(18)定权是可行的。
PolInSAR植被高反演模型只是复数平差模型的一个范例,实际上在大地测量的其他领域广泛存在。目前在实数域最小二乘平差模型中已形成了一整套成熟的参数估计和精度评定的理论,而复数域测量相应的计算方法和精度评定尚无系统的理论与方法。因此,把局限于实数域的经典最小二乘平差理论拓展到复数域,系统研究复数域平差模型的理论与方法,并根据复数本身的特性添加新的元素,拟建立起一整套复数非线性最小二乘的参数估计和精度评定的理论是今后研究的主要方向。
| [1] | TREUHAFT R N, MADSEN S N, MOGHADDAM M, et al. Vegetation Characteristics and Underlying Topography from Interferolnetric Radar[J]. Radio Science, 1996, 31(6): 1449-1485. |
| [2] | CLOUDE S R, PAPATHANASSIOU K P. Polarimetric SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(5): 1551-1565. |
| [3] | TREUHAFT R N, SIQUEIRA P R. Vertical Structure of Vegetated Land Surfaces from Interferometric and Polarimetric Radar[J]. Radio Science, 2000, 35(1): 141-177. |
| [4] | PAPATHANASSIOU K P, CLOUDE S R. Single-baseline Polarimetric SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(11): 2352-2363. |
| [5] | CLOUDE S R, PAPATHANASSIOU K P. Three-stage Inversion Process for Polarimetric SAR Interferometry[J]. IEE Proceedings: Radar, Sonar and Navigation, 2003, 150(3): 125-134. |
| [6] | GILBOA G, SOCHEN N. Image Enhancement and Denoising by Complex Diffusion Processes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(8): 1020-1036. |
| [7] | GRIGOLI F, CESCA S, DAHM T, KRIEGER L. A Complex Linear Least-squares Method to Derive Relative and Absolute Orientations of Seismic Sensors[J].Geophysical Journal International, 2012, 188(3): 1243-1254. |
| [8] | OPPENHEIM A V, LIM J S. The Importance of Phase in Signals[J]. Proceedings of the IEEE, 1981, 69(5): 529- 541. |
| [9] | TAEIGHAT A, SAYED A H. Least Mean-phase Adaptive Filters with Application to Communications Systems[J]. IEEE Signal Processing Letters, 2012, 11(2): 220-223. |
| [10] | DANILO P M, SU L G, KAZUYUKI A. Sequential Data Fusion via Vector Spaces: Fusion of Heterogeneous Data in the Complex Domain[J]. The Journal of VLSI Signal Processing, 2007, 48(1): 99-108. |
| [11] | THOMAS P. Navigation Signal Processing for GNSS Software Receivers[M]. Boston: Artech House Publishers, 2010. |
| [12] | GU Xiangqian, KANG Hongwen, CAO Hongxing. The Least-square Method in Complex Number Domain[J]. Progress in Natural Science, 2006, 16(1): 49-54. (谷湘潜, 康红文, 曹洪兴. 复数域内的最小二乘法[J]. 自然科学进展, 2006, 16(1): 49-54.). |
| [13] | LI Mengxia, CHEN Zhong. The Modification of Least Square Method(LSM) in the Complex Field[J]. Journal of Yangtze University: Natural Science Edition, 2008, 5(3): 7-8. (李梦霞, 陈忠. 复数域内最小二乘法的一种改进[J] . 长江大学学报: 自然科学版, 2008, 5(3): 7-8.). |
| [14] | MILLER K S. Complex Linear Least Squares[J]. SIAM Review, 1973, 15(4): 706-726. |
| [15] | WU Yirong, HONG Wen, WANG Yanping. The Current Status and Implications of Polarimetric SAR Interferometry[J]. Journal of Electronics & Information Technology, 2007, 29(5): 1258-1262. (吴一戎, 洪文, 王彦平. 极化干涉SAR的研究现状与启示[J]. 电子信息学报, 2007, 29(5): 1258-1262.) . |
| [16] | LI Tingwei, LIANG Diannong, ZHU Jubo. A Review of Inversion of the Forest Height by Polarimetric Interferometric SAR[J]. Remote Sensing Information, 2009, 3: 85-90. (李廷伟, 梁甸农, 朱炬波. 极化干涉SAR森林高度反演综述[J]. 遥感信息, 2009(3): 85-90.) . |
| [17] | YANG Lei, ZHAO Yongjun, WANG Zhigang. Polarimetric Interferometric SAR Data Analysis Based on TLS-ESPRIT of Joint Estimation of Phase and Power[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 163-168. (杨磊, 赵拥军, 王志刚. 基于功率和相位联合估计TLS-ESPRIT算法的极化干涉SAR数据分析[J]. 测绘学报, 2007, 36(2): 163-168.) . |
| [18] | TAN Lulu, YANG Libo, YANG Ruliang. Investigation of Tree Height Retrieval with Polarimetric SAR Interferometry Based on ESPRIT Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(3): 296-300. (谈璐璐, 杨立波, 杨汝良. 基于ESPRIT算法的极化干涉SAR植被高度反演研究[J]. 测绘学报, 2011, 40(3): 296-300.) . |
| [19] | LUO Huanming. Models and Methods of Extracting Forest Structure Information by Polarimetric SAR Interferometry[D]. Chengdu: University of Electronic Science and Technology of China, 2011. (罗环敏. 基于极化干涉SAR的森林结构信息提取模型与方法[D] . 成都:电子科技大学,2011.) . |
| [20] | WANG Xinzhou. Non-linear Model Parameter Estimation Theory and Application[M]. Wuhan: Wuhan University Press, 2002. (王新洲. 非线性模型参数估计理论与应用[M]. 武汉:武汉大学出版社, 2002.) . |
| [21] | SEYMOUR M S, CUMMING I G. Maximum Likelihood Estimation for SAR Interferometry[C]//Proceedings of International IGARSS '94: Surface and Atmospheric Remote Sensing: Technologies, Data Analysis and Interpretation. New York: IEEE, 1994, 4: 2272-2275. |
| [22] | FREEMAN A, DURDEN S L. A Three-component Scattering Model for Polarimetric SAR Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(3): 963-973. |
| [23] | WILLIAMS M L. PolSARproSim Design Document and Algorithm Specification(u1.0)[R/OL]. (2006-12-01)[2012-03-20]. http://earth.eo.esa.int/polsarpro/Manuals/PolSARproSim_Design.pdf. |