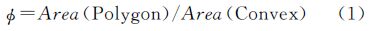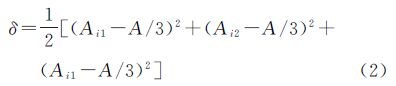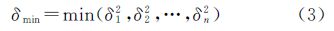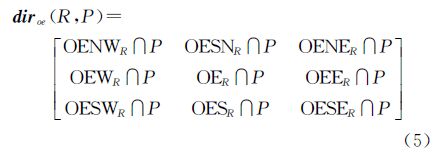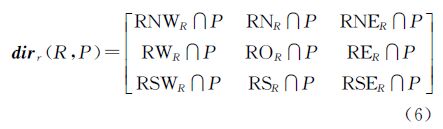空间关系描述模型反映地理目标空间结构和布局方向特征,是人类空间认知习惯在空间数据库中的反映及描述,是空间查询和存储的基础[1, 2]。方向关系描述空间目标在空间上的顺序或位置关系,反映了两个空间目标间的指向关系[3],是最常用的相对定位方法。在地理信息科学研究中,方向关系理论被广泛应用于空间数据建模、空间查询及推理、空间分析、决策支持、面向对象的遥感影像处理、智能空间信息处理等领域[1, 3, 4, 5, 6, 7]。例如,利用已知的方向关系条件进行模糊方向关系语义查询和定位,是智能空间信息处理的重要研究内容之一。在遥感图像检索研究中,将方向关系等空间关系特征作为空间相似度匹配依据,可有效提高影像检索的精度和效率[7]。
方向关系描述模型实现了方向关系约束的定量描述,是提取方向关系语义特征的关键。方向关系描述模型包括定量和定性描述两大类[3],由于空间问题所固有的复杂性和不确定性,方向关系表达和推理普遍采用定性描述模型[1, 8, 9]。现有定性方向关系描述模型根据其方向区域的划分方式,可划分为锥形模型、投影模型及基于Voronoi图模型等[8]。锥形模型及其扩展模型将参考目标抽象为一个点,无法反映线/面参考目标形状和大小的影响,其描述精度较差,适用于点参考目标方向关系描述。投影模型将目标投影到特定的坐标轴上,由参考目标及源目标投影间的关系定义方向关系,对目标形状和大小较敏感,在一定程度上克服了锥形模型描述缺陷。基于Voronoi图模型通过参考目标的Voronoi图与源目标的相交关系来描述方向关系,在模型的适用性等方面存在优势[9]。但由第2节的分析可以得知,现有投影模型和基于Voronoi图模型用几何近似替代参考目标的真实边界,无法准确描述几何近似范围内的定性方向关系。针对这些问题,本文提出一种基于拓扑参考的定性方向关系矩阵模型,将拓扑参考引入方向关系描述,在拓扑划分基础上重新进行方向区域划分,从根本上解决MBR区域定性方向关系描述问题,实现复杂拓扑关系目标定性方向关系描述。
2 现有方向关系定性描述模型分析方向关系的形式化描述主要包括3个基本要素,即源目标(待确定方向的目标)、参考目标(确定源目标方向的参考物体)及方向参考体系[3]。因此,定性方向关系描述精度取决于描述模型对源目标及参考目标形状和大小的敏感程度及方向参考定义的合理性。
锥形模型利用参考目标指向线将空间目标及其周围区域划分为带有方向性的互斥的若干个锥形区域(4个或8个),通过源目标与方向区域的相交情况来描述方向关系[8],对点参考目标的方向区域划分符合方向认知习惯。但由于将线/面参考目标抽象为一个点,当空间目标之间的距离相对于自身大小较近的时候,可能出现描述错误。针对原锥形模型的描述缺陷,文献[10]基于参考目标的MBR范围重新划分方向关系区域;文献[11]提出四半区域模型,以参考目标MBR相邻顶点的4条方向线及其交点的连线为参考,将参考目标的外部空间划分为4个半无限区域,将面参考目标抽象为一根连接线,在一定程度上提高了描述精度,但无法根除其描述缺陷。
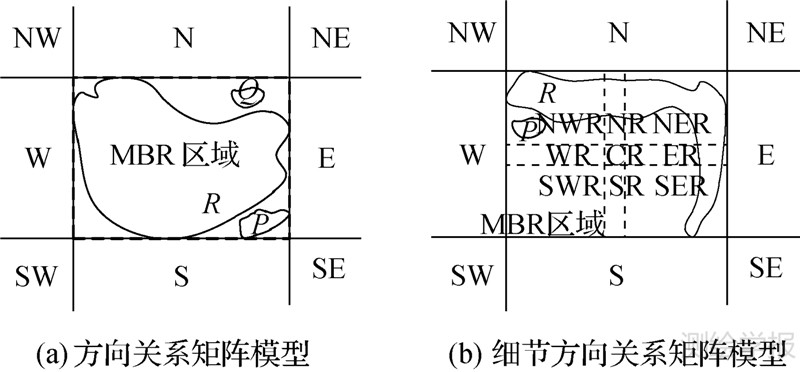
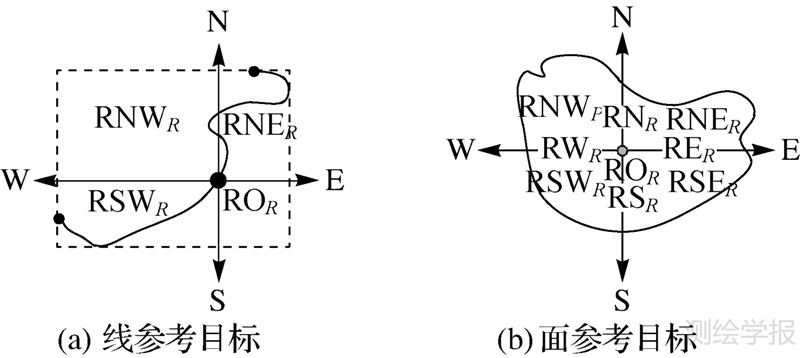
投影模型将空间目标投影到特定的坐标轴上,根据目标投影(正射投影或斜率投影)间的关系来定义方向关系[12],代表性模型包括2DString投影模型[13, 14]、MBR模型[10, 15]及方向关系矩阵模型[1]等。2DString及其扩展模型利用空间目标在X轴和Y轴方向的投影字符串定义方向关系,将二维空间方向关系特征转换为一维空间方向关系表达,其方向分辨能力有限。MBR模型以参考目标和源目标的MBR范围替代参考目标和源目标,对目标的形状和大小敏感度较差。方向关系矩阵模型以参考目标MBR区域为参考中心划分方向区域,利用源目标与9个方向区域相交的3×3矩阵定义方向关系,对源目标的形状和大小敏感。但由于以MBR拟合参考目标,如图 1(a)所示,方向关系矩阵模型无法分辨MBR区域内的方向关系。针对原方向关系矩阵模型的描述缺陷,文献[16]提出细节方向关系矩阵模型,将MBR区域细分为参考目标的边界、内部和环部,利用MBR中心点及指定高宽矩形的延长线将MBR区域划分为9个矩形区域,提高了模型的描述精度。但由于忽略了不同拓扑区域中方向参考中心的变化,如图 1(b)所示,当参考目标为凹多边形时,细节模型对于其中心区的定义可能位于参考目标外部,与认知习惯不一致。
|
| 图 1 方向关系矩阵及细节方向关系矩阵对MBR的描述 Fig. 1 Description of MBR based on direction-relation matrix and detailed direction-relation matrix |
基于Voronoi 图的模型通过参考目标的Voronoi 图与源目标的关系来描述和定义方向关系。其代表模型包括:文献[9]用参考目标MBR 与Voronoi 区域边界线之间的关系来定义方向关系;文献[3]通过建立与空间目标间指向线的法线比较近似的方向Voronoi 图来描述空间目标间的方向关系。Voronoi模型在模型适用性等方面存在优势,但Voronoi多边形同样是目标的几何拟合,无法避免描述精度缺陷。
考虑到其他空间关系对于方向关系描述的相互约束关系,一些学者研究方向关系与拓扑关系、度量关系等其他空间关系的组合及细化模型[17, 18, 19],通过增加约束条件提高描述模型的表达精度。但是,现有大多数模型是方向关系与拓扑关系在表达模型层次上的组合,并没有考虑拓扑关系对于方向关系定义的影响。例如,文献[6]在方向关系矩阵的基础上,利用源目标与9个方向区域边界线之间的拓扑关系来细化方向关系描述。但是,拓扑细化模型仅考虑了源目标与方向关系区域边界线的拓扑关系,没有考虑源目标与参考目标的拓扑关系对于方向关系描述的影响,难以区分MBR区域内不同拓扑关系目标的方向关系。
综上所述,现有定性方向关系描述模型主要存在问题包括:① 用点、线、MBR范围拟合参考目标,对于目标的形状和大小敏感度较差,大大限制了描述模型精度;② 现有组合和细化模型没有考虑拓扑关系对方向关系参考定义的影响,无法从根本上解决复杂拓扑关系目标的方向关系描述问题。
3 基于拓扑参考的定性方向关系矩阵模型由第2节的分析可得知,锥形模型、投影模型及基于Voronoi 图模型都存在由简化目标边界导致的描述缺陷,解决关键在于保留原目标真实边界,对不同拓扑划分空间定义合理的方向关系参考,提高模型描述精度。
3.1 空间目标定义鉴于地理空间目标的特点及复杂性,文献[17]以组合拓扑为工具,提出了拓扑胞腔(topological cell)理论,奠定了空间数据模型的数学基础。随后,拓扑胞腔理论的发展逐渐形成了现有GIS空间数据模型标准。文献[18]对代数拓扑学中的单纯形(simplex)及单纯复形(simplicial complex)概念进行拓展,将单纯形的凸集约束放宽,定义了胞腔(cell)及胞腔复形(simplicial complexes),并给出不同维数的空间目标及其基本操作定义。文献[19]在此基础上给出拓扑意义上的简单空间目标(n维胞腔A)的闭包、边界、内部及外部的定义,将胞腔及胞腔复形定义应用于空间目标的定义中,分别定义了GIS中的点、线、面目标,即:① 点为二维空间中的一个单独的0维胞腔;② 线为由相互连接的,不相交且无闭合回路的1维胞腔复形构成的序列;③ 面是二维空间中的一个内部不为空的二维胞腔复形[19]。
3.2 基于拓扑参考的方向区域划分拓扑关系对于方向关系的约束主要表现为不同拓扑划分中方向关系参考的变化。因此,方向区域划分首先要在空间目标定义基础上进行拓扑划分,然后对不同的拓扑划分空间定义拓扑参考,将其与原有方向区域划分方法综合,最后得到基于拓扑参考的方向区域划分。
现有拓扑关系描述模型可划分为基于目标分解和基于目标整体的模型两大类[11]。基于目标分解拓扑关系模型的代表性模型4交模型将空间目标看作是边界点和内部点的集合,9交模型对4交模型进行拓展,将拓扑空间进一步划分为内部、边界及外部3个部分。4交模型及9交模型在空间数据存储、空间分析等领域得到了广泛的应用,但是,“补”的定义一方面存在无限性、重叠大、空间实体定义不足、不能表达空间邻近关系等缺陷[12, 20],另一方面,二维空间中线段的拓扑划分会出现内部与外部直接相接的问题,违背了拓扑学中基本的约旦定理[21]。基于目标整体的RCC模型及2DString模型,在区分能力及复杂性描述方面存在不足。针对这些问题,文献[21]提出一种基于目标整体的描述方法,利用空间目标及目标的Voronoi区域之间的交、并、被差、差、对称差等算子实现拓扑关系表达,克服了分解模型拓扑不一致性缺陷;文献[22, 23]在此基础上,将空间目标看作一个整体,提出一种基于目标整体交/差、欧拉数的地籍实体拓扑关系计算方法,用空间目标间的交、差两种集合操作算子来描述其拓扑关系,克服了原有基于Voronoi区域模型的非同时性目标间拓扑关系表达缺陷。
方向区域划分方面,基于投影的方向关系矩阵模型的方向区域划分与方向认知习惯一致,且具有以下优点:①与基于经纬度的地球定位结构一致[24];②与锥形模型相比,投影模型具有更高的方向分辨精度[5];③对于空间数据库而言,由于方向关系矩阵模型的方向区域划分是矩形的,与锥形模型相比更容易实现[1];④从数学的角度来看,在二维空间中,其方向区域划分是完备的。因此,本文以方向关系矩阵模型的方向区域划分为基础,将其与拓扑划分进行结合,定义新的方向区域划分。
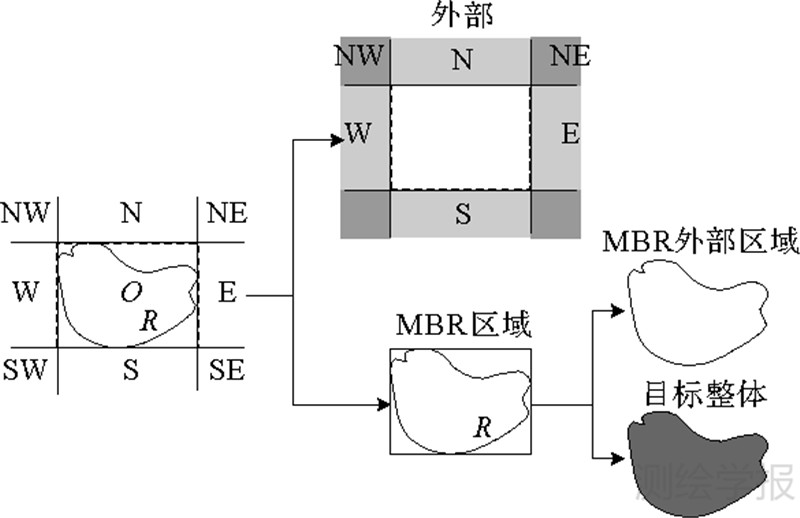
综合以上分析,如图 2所示,新的方向区域划分首先基于参考目标整体,将整个拓扑空间划分为外部及目标整体两大区域,将其与方向关系矩阵模型的9个方向区域进行相交,得到10个区域。其中,外部的8个区域与原有方向关系矩阵模型区域一致,增加的2个区域实质上是对原有MBR区域的拓扑细分。
|
| 图 2 MBR区域的拓扑划分 Fig. 2 The topological division of MBR |
在拓扑划分的基础上,给出新的方向区域定义。
外部的8个方向区域采用外部拓扑参考,由于离参考目标较远,外部拓扑参考将MBR区域整体作为中心,其方向区域定义与原方向关系矩阵模型一致。
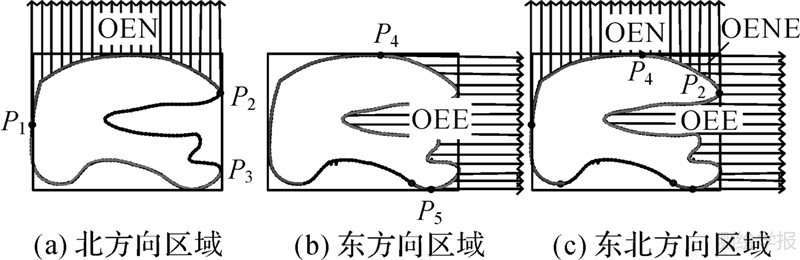
MBR外部区域离参考目标较近,因此,其方向关系定义主要受到参考目标局部边界影响。根据认知习惯,该区域方向关系由参考目标方向指向决定,若某个区域为两个方向指向的重叠区域,则为复合方向区域。如图 3所示,北方向区域为参考目标北方向指向区域(图 3(a)),东方向区域为参考目标东方向指向区域(图 3(b)),东北方向区域为北方向和东方向指向重叠区域(图 3(c))。在实际计算中,由方向的自反性,可以源目标到参考目标上的投影距离DN、DE、DS及DW作为判断参数。
|
| 图 3 MBR区域外部方向区域 Fig. 3 The exterior direction tiles of MBR |
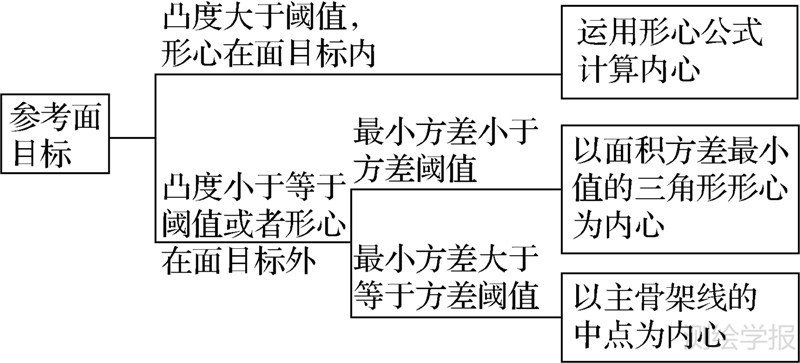
目标整体区域采用目标整体拓扑参考,其定义关键在于确定线/面目标的参考中心。若将参考中心定义为线/面目标的内心(记作C),根据认知习惯,须满足两个约束条件:① 位于参考目标内部;② 位于参考目标分布的中心区域,能反映参考目标的面积及形状分布。线目标分布通常以长度为衡量指标,因此,将线目标的中点定义为其内心。面目标分布主要以面积为衡量指标,通常以形心作为中心。但凹多边形的形心可能位于目标外部,不满足第一个约束条件。因此,本文参考地图注记中心点多边形骨架线中点定义,采用文献[25]提出的基于约束Delaunay三角网结构的形心方法定义面目标的内心,其计算流程如图 4所示。将面目标边界离散为边界离散点,以三角形不能穿越面边界为约束条件建立Delaunay三角网,把得到的三角形分为3类:Ⅰ类三角形,三角网中的边界节点,其顶点中有一个顶点为骨架线的端点;Ⅱ类三角形,三角网中跨接三角形;Ⅲ类三角形,位于骨架分支的交汇处的三角形。其中,凸度为任意多边形面积与该多边形凸壳面积的比值,即
设Ⅲ类三角形i的3条边截取面状目标的面积为Ai1、Ai2、Ai3,且面目标总面积A=Ai1+Ai2+Ai3,则最小方差的计算公式为
|
| 图 4 内心的计算流程 Fig. 4 The computational procedure of incenter |
中心参考点确定后,采用8方向划分,可以得到如图 5所示的方向区域划分。
|
| 图 5 线/面参考目标整体方向区域划分 Fig. 5 The direction tiles of whole line/area reference object |
对应新的方向区域划分,将原有方向关系矩阵模型拓展为外部方向关系矩阵、MBR外部方向关系矩阵及目标整体方向关系矩阵等3个方向关系矩阵,具体定义如下。
定义1:外部方向关系矩阵描述参考目标MBR外部区域的方向关系,记作dire(R,P),定义为
定义2:MBR外部方向关系矩阵描述MBR内参考目标外部区域的方向关系,记作diroe(R,P)定义为
定义3:目标整体方向关系矩阵描述参考目标整体区域内的方向关系,记作dirr(R,P),定义为
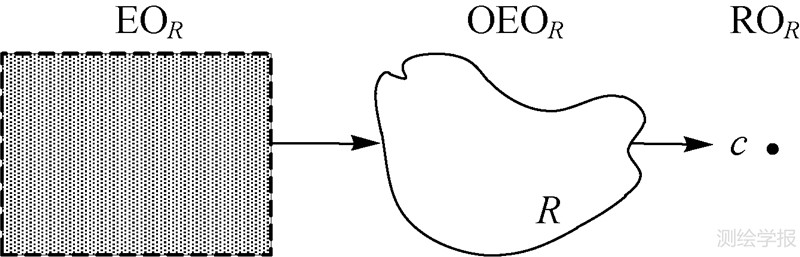
如图 6所示,3个方向关系矩阵中心元素的层次包含关系反映了方向区域划分的连续性和完整性。
|
| 图 6 层次方向关系矩阵中心元素的包含关系 Fig. 6 The relationships between the cores of hierarchical direction-relation matrixes |
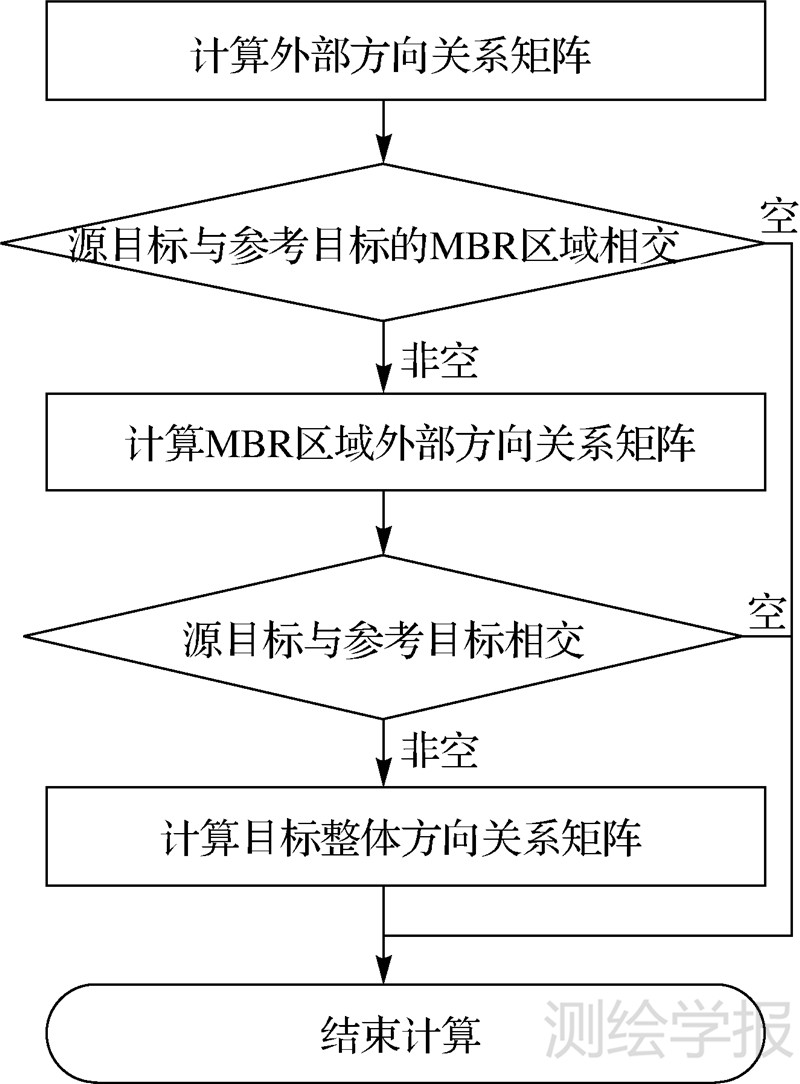
为了提高计算效率,新模型采用分级计算策略,如图 7所示,按照外部、MBR外部、目标整体的顺序来进行方向关系矩阵计算,每个方向矩阵计算完后,根据其中心元素的取值来决定是否继续计算:中心元素值若为空,停止计算;反之,继续计算。
|
| 图 7 层次方向关系矩阵的计算流程 Fig. 7 The flow of hierarchical matrixes |
与原方向关系矩阵模型及细节方向关系矩阵模型相比,新模型在拓扑划分基础上建立不同拓扑区域的方向参考,实现了MBR区域内复杂拓扑关系目标定性方向关系的精确描述。
4 试验分析4.1 与MBR模型及方向关系矩阵模型的比对试验
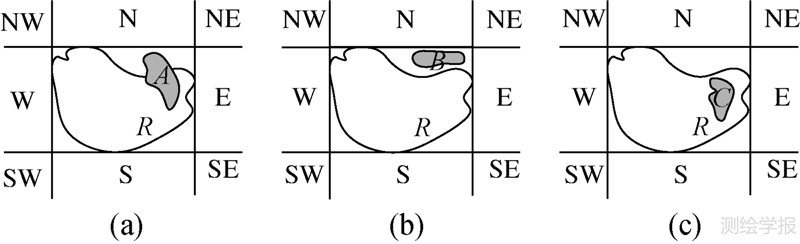
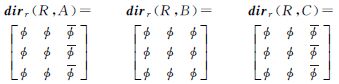
由于新模型保留了参考目标的原有边界,并对MBR区域进行拓扑细分,能够克服MBR模型及方向关系矩阵模型的MBR描述缺陷。对3个模型的描述能力进行比对试验,如图 8所示,选择MBR内不同拓扑关系的3个源目标,其中,A与R相交,B与R相离,C位于R的内部,分别用3个模型对其进行方向关系描述,描述结果如表 1所示。从试验结果不难看出:① MBR模型和方向关系矩阵模型对3个目标的描述结果相同,无法区分MBR区域内的方向;② 新模型不仅能分辨不同目标的方向关系,且反映了目标所在的拓扑划分,实现了复杂拓扑关系目标的方向关系描述。
|
| 图 8 MBR内不同拓扑关系目标 Fig. 8 Objects of different topological relations in MBR |
| A | B | C | |
| MBR模型 |  | ||
| 方向关系矩阵模型 |  | ||
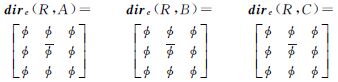 | |||
| 新模型 | 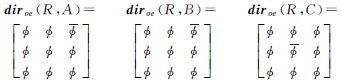 | ||
 | |||
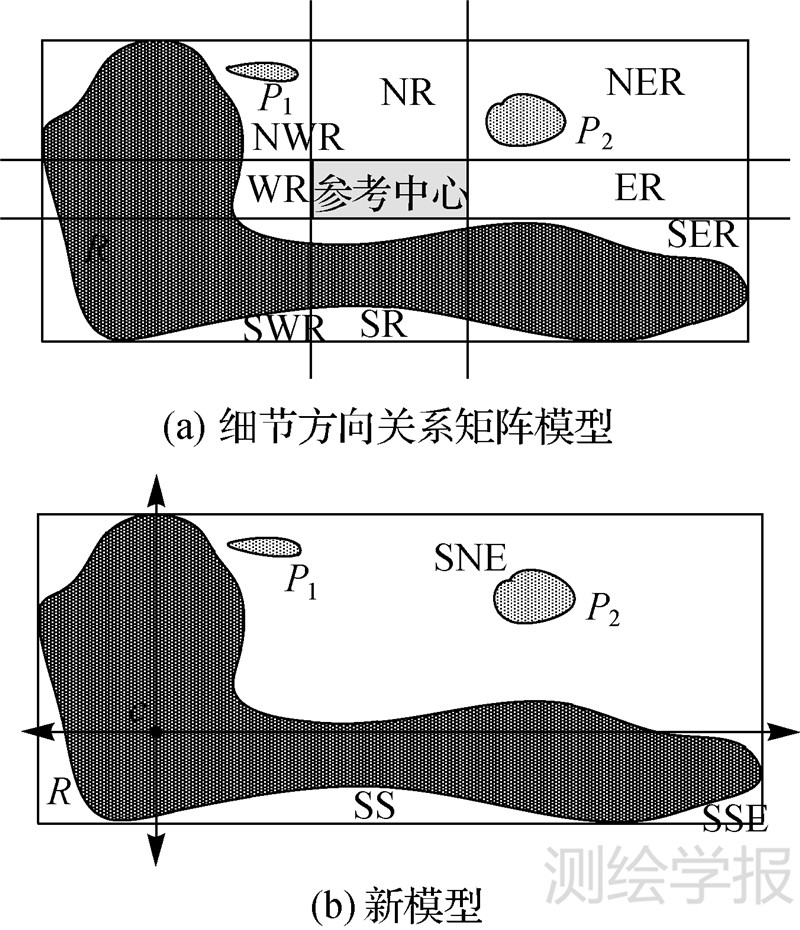
拓扑细化描述模型仅考虑了MBR外部区域中源目标与9个方向区域延长线的拓扑关系,无法分辨MBR内不同拓扑关系目标的方向关系。如图 9(a),细节方向关系矩阵模型虽能分辨MBR内的目标,但对于凹面目标中心定义可能与认知习惯不符。如图 9(b),新模型考虑了不同拓扑划分中方向关系参考中心的变化,描述结果更加接近认知习惯。3个模型对图 9的空间目标方向关系描述结果如表 2所示。
|
| 图 9 凹多边形方向区域划分 Fig. 9 The direction tiles of concave polygon |
| P1 | P2 | 描述含义 | |
| 拓扑细化模型 | 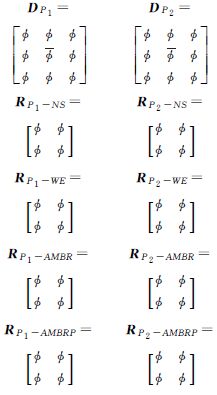 | P1位于参考目标MBR区域,P2位于参考目标MBR区域 | |
| 细节方向关系矩阵 |  | P1位于参考目标环部西北方向,P2位于参考目标环部东北方向 | |
| 新模型 |  | P1和P2目标均位于参考目标MBR外部区域东北方向 | |
从试验结果不难发现,拓扑细化模型无法分辨两个目标的方向关系差异。细节模型虽然能区分两个目标的方向,但其将MBR区域的中心直接作为MBR外部区域(环部)的中心,不考虑局部边界对方向的影响,其描述结果与认知习惯不符。新模型考虑了局部边界对源目标方向的影响,更加贴近方向认知习惯。
5 结 论针对现有定性方向关系描述模型对于MBR的描述缺陷,将拓扑参考引入方向关系定义,提出了基于拓扑参考的定性方向关系矩阵模型。试验结果表明,新模型具备以下特点:① 能够分辨MBR区域的不同拓扑划分,从根本上解决了复杂拓扑关系目标方向关系描述问题,提高了模型的准确性和精确性;② 根据认知习惯,新模型对于不同拓扑区域建立方向关系拓扑参考,解决了凹多边形的参考中心定位问题;③ 采用分级计算策略,计算量由目标拓扑关系而定,在提高描述精度同时,有效控制了计算量。
定性方向关系描述模型是定性模糊概念定量描述的基础,本文所提出的新模型虽然改进了原有模型的方向关系区域划分及描述,但尚未解决定性描述与定量描述间转换问题,因此,下一步的研究将集中在以下方面:① 将定性描述模型与定量描述模型相结合,建立定性到定量间的转换模型;② 将确定性空间目标拓展到模糊目标,研究模糊目标方向关系特征描述模型;③ 将新模型应用于空间查询及检索等应用领域,验证和改进模型的性能。
| [1] | GOYAL R K. Similarity Assessment for Cardinal Directions between Extended Spatial Objects [D]. Maine: The University of Maine,2000. |
| [2] | LI Deren, ZHU Qing, ZHU Xinyan, et al. Task-based Remote Sensing Information Focus Service [M]. Beijing: Science Press, 2011. (李德仁, 朱庆, 朱欣焰, 等. 面向任务的遥感信息聚焦服务[M]. 北京: 科学出版社, 2011.) |
| [3] | YAN Haowen,GUO Renzhong. Theorization of Directional Relationship Description Based on Voronoi Diagram [J]. Geomatics and Information Science of Wuhan University, 2002,27(3): 306-310. (闫浩文,郭仁忠. 用Voronoi图描述空间方向关系的理论依据[J].武汉大学学报:信息科学版,2002,27(3): 306-310.) |
| [4] | KULIK L,KLIPPEL A. Reasoning about Cardinal Directions Using Grid as Qualitative Geographic Coordinates [C]//Spatial Information Theory-cognitive and Computational Foundations of Geographic Information Science COSIT 99.[S.l.]:COSIT,1999: 205-220. |
| [5] | FRANK. Qualitative Spatial Reasoning: Cardinal Directions as an Example [J]. International Tree-an Intelligent Graphical Zoom, Computers & Graphics, 1996, 18(6): 823-829. |
| [6] | CAO Han, CHEN Jun, DU Daosheng. Qualitative Extention Description for Cardinal Directions of Spatial Object [J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(2): 162-167. (曹菡, 陈军, 杜道生. 空间目标方向关系的定性扩展描述[J]. 测绘学报, 2001, 30(2): 162-167.) |
| [7] | CHENG Qimin. Remote Sensing Image Retrieval Technologies [M]. Wuhan: Wuhan University Press, 2011:16.(程起敏. 遥感图像检索技术[M]. 武汉:武汉大学出版社, 2011:16.) |
| [8] | XIA Yu, ZHU Xinyan, LIN Deren, et al. Research on Spatial Directional Relation Description Model [J]. Science of Surveying and Mapping, 2007, 32(5):94-97. (夏宇,朱欣焰,李德仁,等. GIS空间方向关系形式化描述模型分析[J].测绘科学, 2007, 32(5):94-97.) |
| [9] | LI Chengming, ZHU Yinghao, CHEN Jun. Directional Relation Description and Determination Based on Voronoi Diagram in GIS [J]. Journal of the PLA Institute of Surveying and Mapping, 1998, 19(2): 117-120. (李成名,朱英浩,陈军.利用Voronoi图形式化描述和判断GIS中的方向关系[J].解放军测绘学院学报,1998, 19(2): 117-120.) |
| [10] | PEUQUET D,ZHAN C X. An Algorithm to Determine the Directional Relationship between Arbitrary-Shape Polygons in the Plane [J]. Pattern Recognition, 1987, 20 (1):65-74. |
| [11] | ABDELMOTY A I,WILLIAMS M H. Approaches to the Representation of Qualitative Spatial Relationship for Geographic Database [C]// Proceedings of Advanced Geographic Data Modeling.[S.l.]:Netherlands Geodetic Commission,1994: 204- 216. |
| [12] | CHEN Jun,ZHAO Renliang. Spatial Relations in GIS: a Survey on Its Key Issues and Research Progress [J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(2): 95-102. (陈军, 赵仁亮.GIS空间关系的基本问题与研究进展[J]. 测绘学报, 1999, 28(2): 95-102.) |
| [13] | CHANG S K, SHI Q S,YAN C W. Iconic Indexing by 2-D String[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1987, 9(6): 413-428. |
| [14] | CHANG S K,JURGERT E. Symbolic Projection for Image Information Retrieval and Spatial Reasoning [M]. London: Academic Press,1996. |
| [15] | MUKERJEE A,JOE G. A Qualitative Model for Space [C]//Proceedings of Eighth National Conference on Artificial Intelligence.Boston:[s.n.], 1990:721-727. |
| [16] | DU Shihong. Research on Theoretics and Methods of Fuzzy Description and Composite Reasoning of Spatial Relations [D]. Beijing: Graduate University of Chinese Academy of Sciences, 2004. (杜世宏. 空间关系模糊描述及组合推理的理论和方法研究 [D]. 北京: 中国科学院研究生院, 2004.) |
| [17] | CORBETT J P. Topological Principles of Cartography [R].[S.l.]: Bureau of the Census, 1979. |
| [18] | FRANK A. Cell Graph: A Provable Correct Method for the Storage of Geometry [C]//Proceedings of Second International Symposium on Spatial Data Handling. Seattle:[s.n.], 1986. |
| [19] | EGENHOFER M,HERRING J. A Mathematical Framework for the Definitions of Topological Relationships[C]//Proceedings of the 4th International Symposium on Spatial Data Handling. [S.l.]: SDH,1990. |
| [20] | LI Chengming, CHEN Jun. The Nine-intersection Model for Describing Spatial Relation [J]. Journal of Wuhan Technical University of Surveying and Mapping, 1997, 22(3):207-211. (李成明,陈军. 空间关系描述的9-交模型[J]. 武汉测绘科技大学学报,1997, 22(3): 207-211.) |
| [21] | LI Z L, ZHAO R, CHEN J. A Voronoi-based Spatial Algebra for Spatial Relations [J]. Progress in Natural Science, 2002, 12: 528-536. |
| [22] | ZHOU Xiaoguang, CHEN Jun, LI Zhilin,et al. Computation of Topological Relations between Cadastral Objects Based on Euler-number [J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(3):291-298. (周晓光,陈军,李志林,等. 基于欧拉数的地籍拓扑关系计算与应用[J]. 测绘学报, 2006, 35(3):291-298.) |
| [23] | ZHOU Xiaoguang, CHEN Jun, ZHAN F,et al. A Euler-number-based Topological Computation Model for Land Parcel Database Updating [J]. International Journal of Geographical Information Science, 2013,51(5):23-27. |
| [24] | KULIK L,KLIPPEL A. Reasoning about Cardinal Directions Using Grid as Qualitative Geographic Coordinates [C]//Proceedings of Spatial Information Theory-cognitive and Computational Foundations of Geographic Information Science COSIT99.Stade:[s.n.], 1999: 205-220. |
| [25] | CHEN Tao,AI Tinghua. Automatic Extraction of Skeleton and Center of Area Feature [J]. Geomatics and Information Science of Wuhan University, 2004, 29(5): 443-446. (陈涛, 艾延华.多边形骨架线与形心自动搜寻算法研究[J]. 武汉大学学报:信息科学版, 2004, 29(5): 443-446.) |