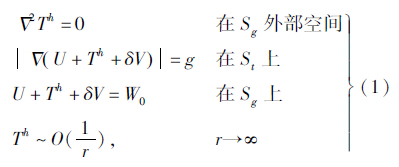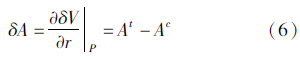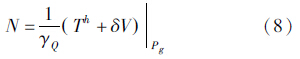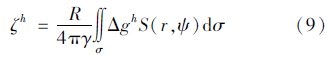1 引言
大地水准面是地球重力场中代表地球形状且与平均海平面最为密合的重力等位面，由地球物质引力和自转离心力及选定的潮汐系统决定，是大地测量学描述包括海洋在内的地球表面地形起伏的理想参考面，即高程的起算面。全球导航卫星系统(GNSS)可简单廉价快速测定地面点的大地纬度、大地经度和大地高，但大地高是以参考椭球面为基准面的几何高，两点间高差与重力位差无直接关系，不能标示水的流速和流向，因此，不能用于工程建设。GNSS测定的大地高结合高精度大地水准面模型可以快速获得精密海拔高程，因此，精密的大地水准面数字模型成为高程基准现代化的关键基础设施，据此将实现传统基于水准测量的地面标石高程基准，向现代基于GNSS测量的数字高程基准转变，从而根本改变高程基准的维持模式和高程测定的作业模式。这种新的维持模式是一种无需建立地面标石的“绿色模式”，不再受地面沉降、洪水、地震、滑坡等自然灾害以及人类活动的影响；新的作业模式是一种地表“无障碍模式”，不受任何诸如山区和水域自然环境所限；也是一种相对“独立测高模式”，改变了传递高程的概念，无传递累积误差影响。GNSS“+”大地水准面模型的测高模式，克服了传统水准测量几乎所有局限性，特别是高投入低效率的缺陷，而且目前可达到国家二等水准精度[1]。
20世纪90年代，中低轨卫星精密定轨精度达到优于1分米水平，由卫星轨道摄动观测数据建立了相应精度序列中长波重力场模型，期间联合多代多任务卫星测高数据，提供了全球海洋分辨率优于5′×5′的测高重力数据。美国通过国际合作，联合利用卫星重力模型，陆地和海洋测高重力数据，研制发布了360阶次EGM96，模型大地水准面精度达到分米级。在此背景下，展望21世纪大地测量发展前景，国际大地测量协会(IAG)在多次国际研讨会上提出，确定“1厘米精度大地水准面”是21世纪大地测量发展的一个全局性战略目标[2, 3]。
GNSS定位技术实现了水平定位现代化，但测定海拔高程的垂向定位仍然停留在传统的水准测量，成为全面实现三维定位现代化发展的“瓶颈”。众所周知，突破的关键是建立高分辨率高精度大地水准面模型，将GNSS观测的大地高转换为海拔高。这一思想激发了精化局部大地水准面的努力，目标是从分米级精度提高到厘米级，从30′×30′分辨率提高到5′×5′。实现此目标，不仅有发展经典理论的难题，也存在可获数据的现实困难。与此同时，若干发达国家20年来实施了不断精化本国大地水准面的计划，我国也同步开展了理论和试验研究，达到了与美国和加拿大相当的水平。
以北美国家为例，美国大地测量局(NGS)20世纪90年代先后推出了GEOID90、GEOID93和分辨率为3′×3′的G9501区域大地水准面模型，3个模型计算方法基本相同。用与GPS水准测定的大地水准面高比较，作误差分析，其中G9501与1889个GPS水准点差值的均方差为±24.8 cm[4, 5, 6, 7]。1996重力大地水准面模型G96SSS的计算采用了粗略的Stokes-Helmert方法，其中Helmert重力异常采用Faye异常近似。GPS水准点加测到2951个，G96SSS与其比较的差值均方差为±15.1 cm，标准差为±15.6 cm，系统偏差为31.4 cm，拟合后的大地水准面GEOID96，分辨率为2′×2′ [8]。1999重力大地水准面G99SSS分辨率为1′×1′，计算方法与G96SSS相同，采用了一些改进措施，包括格网化椭球改正(GEOID96未作椭球改正)，为顾及子午线收敛影响，采用多纬度带格网作地形改正，同时采用最新的GM和W0值确定重力异常和大地水准面的零阶项g0和N0等。GPS水准网点增加到6169个(其中包括了各州自测点)，与G99SSS比较差值的标准差为±21.7 cm。最大的改进是对NAD83椭球坐标基准中的全美陆地GPS基准网点(其中大部分进行了重测)，以及NAVD88高程基准中的GPS水准网作了整体重新平差，GPS椭球高的精度达到±1 cm，被NGS认为是一个“里程碑”的进展[9]。2003重力大地水准面USGG2003(1′×1′)计算方法与G99SSS一脉相承，GPS水准网点增加到14 185点(包括加拿大579点)，与USGG2003比较差值的标准差为±4.8 cm[10]。美国最新的重力大地水准面模型US2009(1′×1′)采用严密Stokes-Helmert方法计算，与位于山区18个州共18 398个GPS水准点分州比较，差值的标准差平均值为±6.3 cm，拟合后的大地水准面模型GEOID09(1′×1′)精度比GEOID03有显著改善，达到±3.0 cm[11]。1990—2009年的20年间，美国平均每3年更新升级国家高程基准(NAVD88)大地水准面模型，为此研发了三代高阶地球重力场模型作参考场，包括360阶OSU91，EGM96和2160阶EGM08，同时不断加密国家GPS水准网点密度，20年提高了10倍，重力大地水准面模型分辨率从5′×5′提高到1′×1′，精度从亚米级提高到厘米级，不断推进高程测量现代化。考虑到NAVD88已知的误差远超GNSS椭球高的精度，NGS正在实施一个利用重力(大地水准面)重新定义NAVD88的10年计划GRAV-D[12]。
加拿大和美国采用同一高程基准NAVD88，类似美国，加拿大在近20年中，先后研发了GSD91、GSD95、CGG2000、CGG2005和CGG2010重力大地水准面，计算方法均采用第二类Helmert凝集地形归算及Stokes-Helmert边值问题理论[13, 14, 15, 16, 17]。重力大地水准面与GPS水准的比较差值的标准差和(偏差)分别为：±0.786 m(-1.107 m)、±0.413 m(-1.006 m)、±0.225 m(-0.637 m)、±0.136 m(-0.420 m)和±0.131 m(-0.506 m)[18]。
20世纪，我国利用50年代到70年代实测的全国一、二等天文重力水准资料，形成了我国最初的一、二等天文大地网的高程异常控制网，通过内插得到了1954年北京坐标系下的第一代似大地水准面(CQG60)，总体分辨率大致为200~500 km，精度为±3~±10 m，其主要目的是满足当时建立国家天文大地网地面观测数据归算到参考椭球面对似大地水准面高和垂线偏差数据的需要。70年代末完成了全国天文大地网整体平差，建立了1980西安坐标系，CQG60转换到新坐标系成为CQG80，天文重力水准高程异常控制网转换为HACN80，CQG60和CQG80成为我国第一代似大地水准面。
为发展新一代似大地水准面模型，需考虑研制适于我国应用的全球重力场模型作参考场。文献[19]利用包括我国重力数据在内的全球30′×30′平均空间重力异常，研制成WDM94(360阶)全球重力场模型，期间西安测绘研究所和中科院武汉测量与地球物理研究所也研制了序列类似全球重力场模型。利用全国约22万个重力点值，以及30″×30″ DTM和WDM94模型，计算了中国首个5′×5′重力似大地水准面模型WZD94，与7个地区的GPS水准网作了相对精度的比较，平均标准差为±0.20 m [20]。
2000年利用约40万个地面重力数据、18.75″×28.125″地形数据以及Geosat ERM/GM、ERS-1 ERM/GM、ERS-2 ERM和Topex/Poseidon等卫星测高海洋重力异常数据研制了新一代陆海统一重力似大地水准面(CNGG2000)，以及和GPS水准拟合解的似大地水准面(CQG2000)，分辨率为5′×5′。CNGG2000与全国分布均匀的671个(A级网28点，B级网643点)GPS水准点比较的精度为±0.44 m。按北纬36°和东经108°为界划为东北、东南、西北、西南等4个区，拟合前(后)比较结果分别为±0.33(0.28) m、±0.32(0.30) m、±0.57(0.44) m和±0.53(0.47) m，与CQG80的精度相比，CNGG2000的精度提高了一个多数量级[21]。
本文提出一个新的中国陆地重力似大地水准面CNGG2011模型，概述采用的Stokes-Helmert理论和方法，以及数据处理，利用我国GPS水准资料分析了CNGG2011的全国精度和按省份划分的各省精度情况，最后对进一步发展我国高程基准似大地水准面模型提出若干供参考的设想。
2 Stokes-Helmert方法应用第二类Helmert凝集法，将地形质量凝集为大地水准面上的一个面密度层，密度函数ρc(φ,λ)=ρt(φ,λ)·h(φ,λ)，以此满足按Stokes理论确定大地水准面其外部无质量的要求。这一经过调整质量分布的模型地球，产生“Helmert重力场”，由此可构造以下Stokes-Helmert重力测量边值问题[15, 22]
式中，Th为待求解的Helmert重力场扰动位函数；U为正常重力位；Sg表示大地水准面；St为地形表面；g为重力测量值；W0为已知Sg上的重力位常数；设Vt和Vc分别为地形和凝集层引力位，则式(1)中的这两种引力位之差为 式中，δV即为对大地水准的第一间接影响。式(1)中的第2式是一个非线性边值条件，其球近似线性化形式为
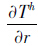为对地心向径r的偏导数
Δgh为Helmert重力异常
式(1)是一个Stokes双边值问题，涉及两个边界面St和Sg。式(5)中下标P、Q、Pg分别表示地面点及其在正常椭球面上的法向投影点和大地水准面上的垂向投影点；γ是正常重力；F是空间改正；ΔgP是空间异常，δA是地形对地面重力的直接影响
式中，At和Ac分别为地形体和凝集层对P点的引力。式(5)中的最后一项为对Sg上Δg的第二间接地形影响，用δS表示 式(1)中的第3式为边界面Sg上解算的扰动位函数(Th+δV)Pg加正常位UPg应等于W0的边值条件。将UPg在点Q上作台劳级数展开，略去二次及高阶项，则有UPg=UQ-γQN，N为大地水准面高，即得到布隆斯公式
式(8)就是用Stokes-Helmert方法计算的大地水准面高。由式(3)和式(5)，由Stokes积分可计算Helmert重力场的高程异常ζh
式中，R为地球平均半径；r是计算点的地心距；ψ是计算点与流动积分点间的地心角距；σ是单位球面。则高程异常由下式计算[23] 式中，δV=δW=Vt-Vc，是地面重力位的变化，即地面地形引力位与凝集层引力位之差。 3 数据处理与数值结果
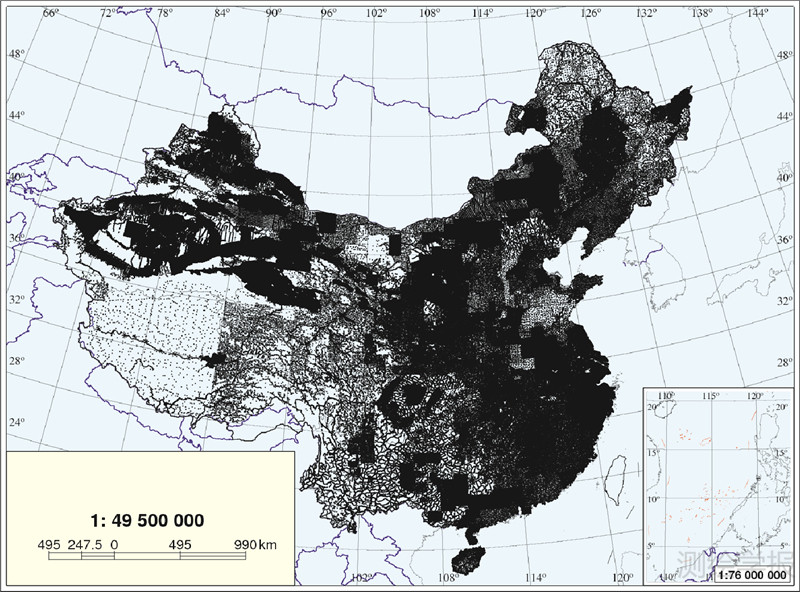
采用的数据包括：1 068 334地面点重力值，大部分由我国地矿和石油部门提供，其密度分布见图 1。地形数据采用美国发布的航天飞机雷达地形测绘任务(shuttle radar topography mission，简称SRTM)数据制作的7.5″×7.5″数值高程模型(DEM)；GPS水准649点，为国家B级点，见图 2。
|
| 图 1 重力数据分布图* Fig. 1 The distribution of gravity observations |
|
| 图 2 全国B级GPS水准点位图* Fig. 2 The distribution of the order B GPS/Leveling |
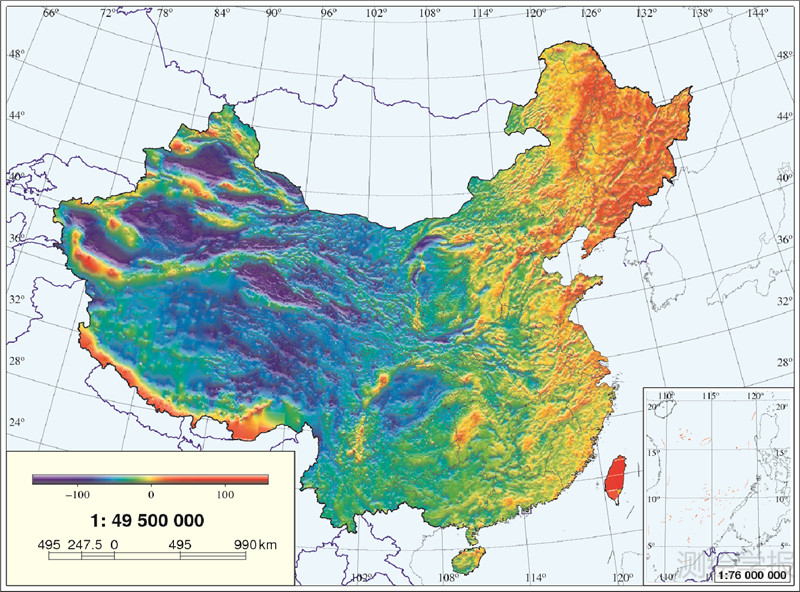
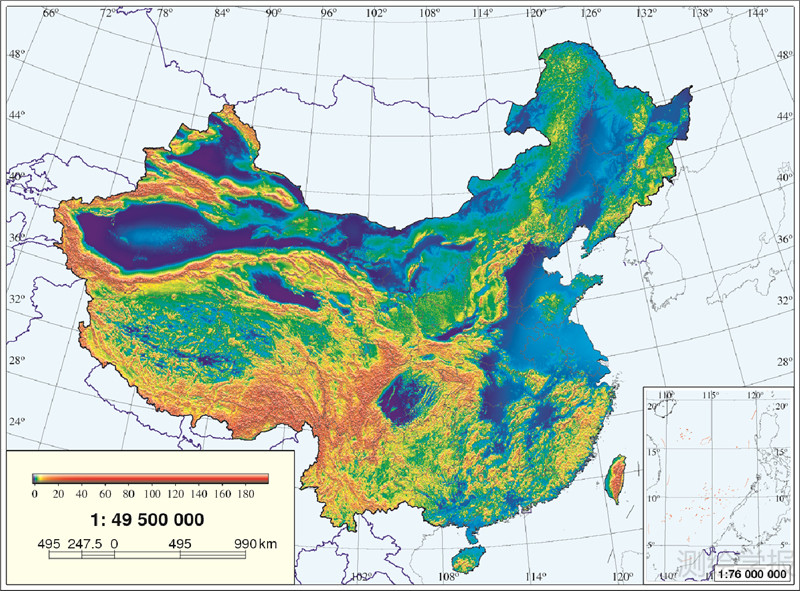
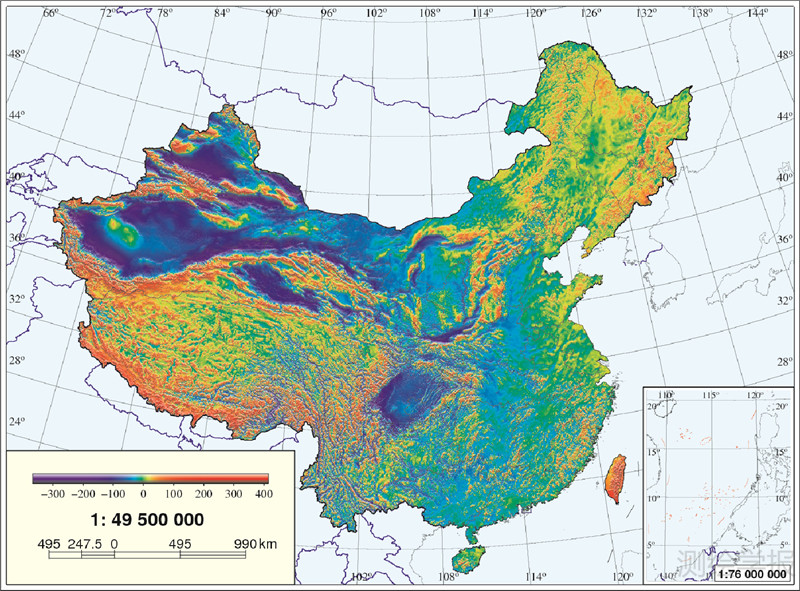
由图 1可以看出，我国西部重力数据稀疏，尤其是青藏高原存在大面积空白区，为计算高分辨率(2′×2′)重力似大地水准面，必须采用最适合的地形重力归算平滑重力场，进行内插格网化。我国地形起伏大变化剧烈，空间重力异常变化呈现高度非线性复杂度，由点值直接取格网平均值误差大。通常采用地形布格归算或地形均衡归算平滑重力异常场。我国布格异常最小值约-600 mGal(1 Gal=1 cm/s2)，最大值约240 mGal，变化幅度近900 mGal，且含系统性变化成分。采用地形均衡归算得到的地形均衡异常比布格异常平滑度高得多，且量值小。本文采用Airy-Heiskanen地形均衡归算模型(均衡抵偿深度取32 km)，计算了我国2′×2′地形均衡异常，如图 3。计算过程的第1步是采用观测高程计算重力点的空间改正和布格片改正；第2步利用7.5″×7.5″ DEM计算每个7.5″×7.5″格网结点的地形改正和均衡改正(图 4所示)；第3步在重力点周围选择适当数量的格网结点，利用双三次多项式内插重力点的地形和均衡改正，由此得到所有重力点的地形均衡异常；第4步，采用连续曲率张力样条格网化算法[24]，将重力点的地形均衡异常内插为30″×30″格网地形均衡异常；第5步，将30″×30″格网地形均衡异常通过双三次多项式内插形成2′×2′格网；最后由7.5″×7.5″格网结点再利用双三次多项式内插2′×2′格网中心点的地形和均衡改正，并从该点的地形均衡中移去，恢复2′×2′格网空间重力异常，见图 5。
|
| 图 3 地形均衡异常* Fig. 3 The topographical-isostatic anomaly |
|
| 图 4 地形质量引起的引力影响(地形改正)* Fig. 4 The gravitational attraction of topographical mass (terrain correction) |
|
| 图 5 空间异常* Fig. 5 The free-air gravity anomaly |
图 6显示了在16 km范围内没有重力数据的2′×2′空白格网区，主要位于我国西部(特别是西藏和新疆)及内蒙古西部。上述重力归算中的地形 改正和均衡改正都采用了顾及地球曲率影响的严密积分公式，积分半径为300 km，在65 km内区使用数值积分，在65~300 km外区由严密一维FFT技术完成。图 4给出了全国7.5″×7.5″地形改正数值模型，最小、最大值分别为-1.69 mGal和199.45 mGal。考虑到均衡改正的一维卷积公式的级数展开收敛速度在近区较慢，为了保证与数值积分结果的一致性，我们将内区半径由65 km扩大到110 km，全国地形均衡异常最小、最大值分别为-166.59 mGal和177.53 mGal。
|
| 图 6 去掉16 km内没有重力观测值的2′×2′格网空间异常*(台湾省专题资料暂缺) Fig. 6 The free-air gravity anomaly after 2′×2 grids without gravity measurements within 16km being marked as blank(The special data of Taiwan Province is not available) |
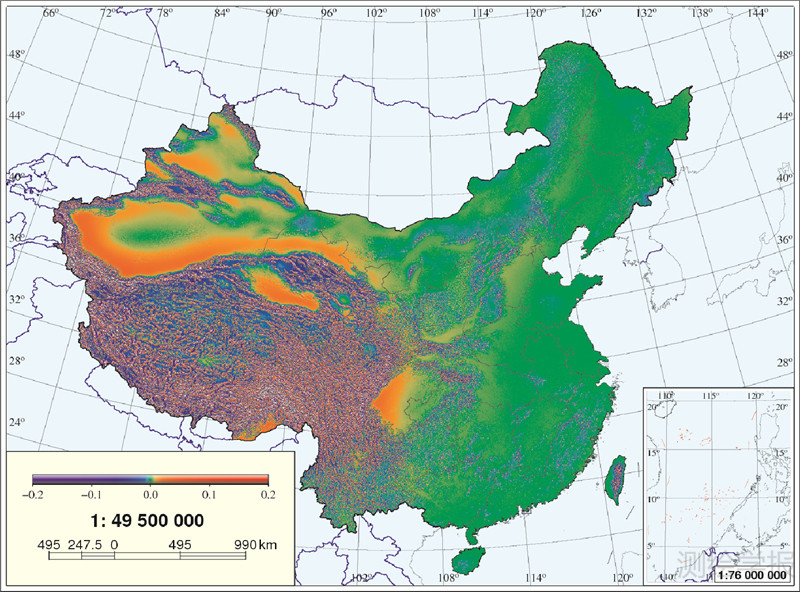
似大地水准面的确定采用Stokes-Helmert方法。主要计算公式为式(2)~(10)。涉及该方法中的3类重力场参量的球面积分运算：第1类是按式(6)计算地形对地面点重力(引力)的直接影响δA，包括计算At和Ac；第2类是按式(2)计算地形对大地水准面上对应计算点的重力(引力)位的间接影响δV，包括计算Vt和Vc；第3类是利用由式(5)计算的Helmert重力异常Δgh，按式(9)计算Helmert重力场的高程异常ζh。最后用式(10)计算要求解的高程异常ζ，由此建立重力似大地水准面数值模型。δV的球面积分方法和地形改正类似，采用的内、外积分半径相同，但其中包含了布格片和局部地形影响。大地水准面间接影响δV/γ的最小、最大值分别为-0.43 m和1.47 m，见图 7。
|
| 图 7 大地水准面的间接影响* Fig. 7 The indirect effects on geoid |
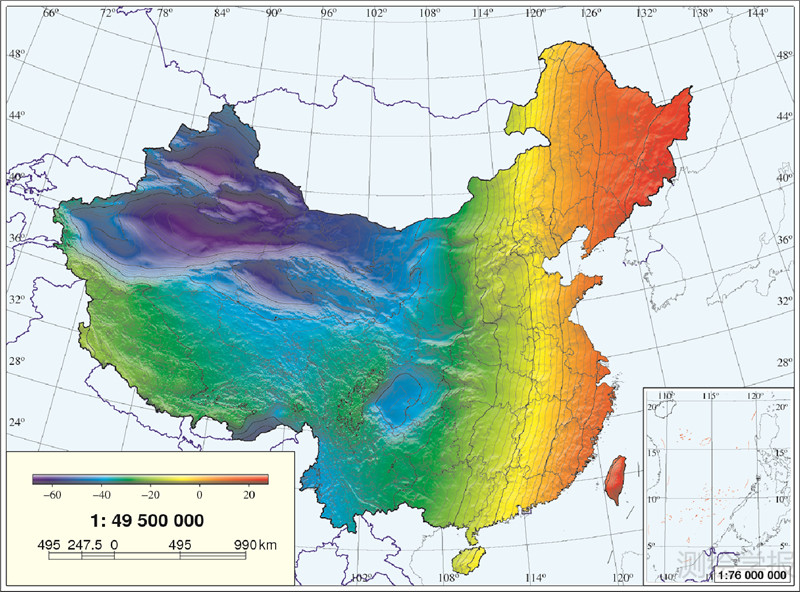
计算重力似大地水准面模型用10个全球重力场模型(EGM96、EGM2008、GGM01C、GGM02C、GGM03C、EIGEN01C、EIGEN03C、EIGEN04C、EIGEN05C和WDM94)作测试比较。经比较，决定采用EIGEN03C为参考场确定中国最新2′×2′重力似大地水准面模型CNGG2011，见图 8，该模型的高程异常最小和最大值分别为-67.901 m和27.996 m。与649个GPS水准点的整体比较，结果列于表 1，其中第2行为移去系统偏差(平均值)-0.161 m后的结果，其最小和最大值分别为-0.585 m和0.407 m，标准差为±0.126 m。用30个省市作局部(区域)比较，GPS水准点总数仍然为649个，但各省向外扩展了15 km，每省市分别采用本身最优秀参考重力场模型，结果列于表 2，由此表可看出，各省市的系统偏差不同，标准差也不同，30个省市平均系统偏差为-0.142 m，平均标准差为±0.062 m。此外，当各省市均采用EIGEN03C为参考场，GPS水准点相同，结果列于表 3，由此表可以看出，与表 2中的对应省市，系统偏差绝对值有10个偏小，20个偏大，2个相等，但标准差则全部偏大。系统偏差的平均值为-0.159 m，大于表 2的平均值，标准差平均值±0.091 m，显著高于表 2的值。对照表 2和表 3的上述比较结果，值得注意的是，参考重力场模型没有统一的最优模型，建立覆盖全国的重力大地水准面模型，和各省区局部模型，应分别采用各自最适宜参考场模型，这是因为全球和局部GPS水准大地水准面所含误差成分和量级不同，需要用不同的参考场模型匹配。分析表 2的结果，以108°E为界分东部和西部省区，东部18个省的平均标准差(精度)为±0.046 m，西部9个省区相应值为±0.106 m。因此就局部区域似大地水准面而言，大致可以认为东部地区平均精度优于±5 cm，西部优于±11 cm；对CNGG2011模型，由表 3分析，东部18省平均标准差(精度)为±0.071 m，西部9省区相应值为±0.138 m，因此大致可以认为此模型在东部地区精度优于±8 cm，西部优于±14 cm。总的估计(包括表 2，表 3)东部地区重力似大地水准面精度，大致平均高于西部地区1倍，西藏的精度为±0.22 m。
|
| 图 8 重力似大地水准面(CNGG2011)* Fig. 8 The gravimetric quasi-geoid (CNGG2011) |
| m | |||||
| 点数 | 最大值 | 最小值 | 平均值 | 均方根 | 标准差 |
| 649 | 0.246 | -0.746 | -0.161 | ±0.205 | ±0.126 |
| 0.407 | -0.585 | 0.000 | ±0.126 | ±0.126 | |
| m |
| 省份 | 模型 | 点数 | 最大值 | 最小值 | 平均值 | 均方根 | 标准差 |
| 安徽 | EIGEN03C | 14 | 0.128 | -0.226 | -0.188 | ±0.190 | ±0.025 |
| 北京 | EGM08 | 5 | -0.012 | -0.043 | -0.031 | ±0.032 | ±0.011 |
| 重庆 | WDM94 | 3 | -0.195 | -0.197 | -0.196 | ±0.196 | ±0.001 |
| 福建 | EIGEN04C | 12 | -0.027 | -0.152 | -0.102 | ±0.110 | ±0.042 |
| 甘肃 | ENGEN01 | 36 | -0.028 | -0.304 | -0.143 | ±0.160 | ±0.071 |
| 广东 | GGM03 | 28 | 0.022 | -0.302 | -0.099 | ±0.117 | ±0.062 |
| 广西 | EGM08 | 25 | 0.146 | -0.190 | -0.077 | ±0.104 | ±0.070 |
| 贵州 | EGM96 | 9 | -0.097 | -0.205 | -0.154 | ±0.159 | ±0.037 |
| 海南 | GGM03 | 6 | -0.069 | -0.135 | -0.089 | ±0.092 | ±0.022 |
| 河北 | GGM03 | 27 | -0.013 | -0.338 | -0.169 | ±0.185 | ±0.074 |
| 黑龙江 | EGM08 | 37 | 0.029 | -0.281 | -0.140 | ±0.153 | ±0.061 |
| 河南 | EIGEN05 | 16 | -0.062 | -0.257 | -0.157 | ±0.165 | ±0.053 |
| 湖北 | WDM94 | 18 | -0.137 | -0.257 | -0.193 | ±0.195 | ±0.029 |
| 湖南 | WDM94 | 17 | -0.079 | -0.278 | -0.151 | ±0.158 | ±0.046 |
| 江苏 | GGM03 | 16 | -0.108 | -0.242 | -0.169 | ±0.174 | ±0.044 |
| 江西 | WDM94 | 19 | -0.102 | -0.218 | -0.165 | ±0.168 | ±0.031 |
| 吉林 | EGM08 | 18 | -0.062 | -0.201 | -0.113 | ±0.118 | ±0.036 |
| 辽宁 | WDM94 | 18 | -0.031 | -0.158 | -0.105 | ±0.111 | ±0.035 |
| 内蒙古 | EGM96 | 90 | 0.207 | -0.266 | -0.084 | ±0.111 | ±0.072 |
| 宁夏 | EIGEN03C | 7 | 0.026 | -0.262 | -0.106 | ±0.151 | ±0.106 |
| 青海 | GGM03C | 37 | 0.134 | -0.361 | -0.170 | ±0.197 | ±0.099 |
| 陕西 | WDM94 | 19 | 0.173 | -0.342 | -0.090 | ±0.152 | ±0.123 |
| 山东 | EIGEN01 | 21 | -0.084 | -0.356 | -0.213 | ±0.221 | ±0.061 |
| 山西 | EIGEN03 | 14 | 0.082 | -0.059 | 0.006 | ±0.038 | ±0.037 |
| 四川 | EGM08 | 32 | 0.083 | -0.425 | -0.228 | ±0.247 | ±0.094 |
| 天津 | EIGEN05 | 3 | -0.117 | -0.243 | -0.183 | ±0.190 | ±0.052 |
| 新疆 | EGM96 | 64 | 0.017 | -0.556 | -0.164 | ±0.204 | ±0.121 |
| 西藏 | EIGEN05 | 55 | 0.279 | -0.740 | -0.191 | ±0.291 | ±0.219 |
| 云南 | ENGEN01 | 27 | -0.048 | -0.397 | -0.244 | ±0.259 | ±0.086 |
| 浙江 | EGM08 | 15 | -0.072 | -0.194 | -0.146 | ±0.148 | ±0.027 |
| m |
| 省份 | 点数 | 最大值 | 最小值 | 平均值 | 均方根 | 标准差 | 省份 | 点数 | 最大值 | 最小值 | 平均值 | 均方根 | 标准差 | |
| 安徽 | 14 | -0.085 | -0.292 | -0.194 | ±0.201 | ±0.053 | 江西 | 19 | -0.046 | -0.217 | -0.136 | ±0.144 | ±0.048 | |
| 北京 | 5 | -0.070 | -0.167 | -0.120 | ±0.125 | ±0.033 | 吉林 | 18 | 0.044 | -0.251 | -0.110 | ±0.134 | ±0.077 | |
| 重庆 | 3 | -0.084 | -0.222 | -0.176 | ±0.187 | ±0.065 | 辽宁 | 18 | -0.024 | -0.256 | -0.117 | ±0.129 | ±0.055 | |
| 福建 | 12 | 0.062 | -0.191 | -0.078 | ±0.108 | ±0.076 | 内蒙古 | 90 | 0.234 | -0.353 | -0.103 | ±0.136 | ±0.088 | |
| 甘肃 | 36 | 0.046 | -0.286 | -0.126 | ±0.151 | ±0.083 | 宁夏 | 7 | -0.014 | -0.660 | -0.162 | ±0.271 | ±0.218 | |
| 广东 | 28 | 0.070 | -0.304 | -0.117 | ±0.146 | ±0.087 | 青海 | 37 | 0.095 | -0.500 | -0.171 | ±0.220 | ±0.139 | |
| 广西 | 25 | 0.131 | -0.273 | -0.123 | ±0.147 | ±0.080 | 陕西 | 19 | 0.216 | -0.338 | -0.151 | ±0.207 | ±0.141 | |
| 贵州 | 9 | -0.091 | -0.271 | -0.190 | ±0.199 | ±0.062 | 山东 | 21 | 0.020 | -0.380 | -0.184 | ±0.204 | ±0.088 | |
| 海南 | 6 | 0.038 | -0.277 | -0.062 | ±0.119 | ±0.102 | 山西 | 14 | -0.019 | -0.222 | -0.122 | ±0.134 | ±0.056 | |
| 河北 | 27 | -0.029 | -0.397 | -0.177 | ±0.199 | ±0.091 | 四川 | 32 | 0.002 | -0.534 | -0.236 | ±0.258 | ±0.106 | |
| 黑龙江 | 37 | -0.010 | -0.323 | -0.146 | ±0.164 | ±0.075 | 天津 | 3 | -0.148 | -0.392 | -0.249 | ±0.270 | ±0.104 | |
| 河南 | 16 | -0.017 | -0.296 | -0.180 | ±0.196 | ±0.078 | 新疆 | 64 | 0.188 | -0.634 | -0.215 | ±0.271 | ±0.164 | |
| 湖北 | 18 | -0.110 | -0.346 | -0.223 | ±0.229 | ±0.051 | 西藏 | 55 | 0.246 | -0.746 | -0.204 | ±0.301 | ±0.221 | |
| 湖南 | 17 | -0.087 | -0.342 | -0.162 | ±0.174 | ±0.062 | 云南 | 27 | 0.012 | -0.470 | -0.218 | ±0.244 | ±0.108 | |
| 江苏 | 16 | -0.032 | -0.308 | -0.184 | ±0.196 | ±0.070 | 浙江 | 15 | 0.001 | -0.176 | -0.128 | ±0.135 | ±0.043 |
本文回顾了近20年国内外精化局部大地水准面模型的概况和发展背景，计算了一个新的2′×2′中国重力和1985国家高程基准似大地水准面数值模型(CNGG2011)。采用了100万余个中国陆地重力数据和美国SRTM 7.5″×7.5″地形高数据，以及649个B级GPS水准点的高程异常数据，并应用了10个全球重力场模型作参考重力场，对CNGG2011和30个省市局部似大地水准面模型作测试比较。计算方法采用了Stokes-Helmert方法。对精度的分析表明，CNGG2011的平均精度为±0.126 m，东部18省的平均精度为±0.071 m，西部9省区为±0.138 m。各省区的局部似大地水准面，平均精度为±0.062 m，东部省为±0.046 m，西部省区为±0.106 m。总的估计，东部地区似大地水准面精度，平均高于西部地区1倍，西藏的精度为±0.22 m。“东高西低”的主要原因是西部地区重力数据稀疏或缺失，存在大面积2′×2′格网重力数据空白，其次是地形变化极复杂，数据内插误差影响大。这是我国进一步精化大地水准面存在的主要问题。
值得讨论的问题是，传统观念认为，GPS水准测量是为建立高程基准大地水准面模型起“控制作用”，但研究已表明，由于一个国家的国土面积有限，GPS水准测定的离散大地水准面高含有较严重的长波误差，同时远离国家高程基准点的水准测量传递误差可达近分米级，重力大地水准面与GPS水准大地水准面的较差含有多种复杂误差成分，过去认为后者精度高于前者，由于新一代卫星重力模型中长波精度有大幅提高，同时计算重力大地水准面的理论方法已有显著改善，例如本文采用的Stokes-Helmert方法，因此建立国家数字高程基准的精度主要取决于重力大地水准面的精度。可以设想，未来将逐步减少工程浩大的GPS水准测量，美国不断加密GPS水准点的发展方向值得反思，它的新10年计划正是这种反思后的决策。另一有关的设想是，根据我国精化大地水准面存在的上述问题，今后进一步的发展方向是利用车载和航空重力测量精化西部地区重力场，但目前航空重力测量，由于西部地区自然环境恶劣，特别在青藏高原地区，难于建立导航基础设施，有人驾驶航空重力测量难以实施，建议研究无人航空重力测量系统的可行性。
| [1] | LI Jiancheng.Study and Progress in Theories and Crucial Techniques of Modern Height Measurement in China[J].Geomatics and Information Science of Wuhan University.2007,32(11):980-987.(李建成.我国现代高程测定关键技术若干问题的研究及进展[J].武汉大学学报:信息科学版,2007,32(11):980-987.) |
| [2] | MCNUTT M K,JUDGE A V.The Super Swell and Mantle Dynamics Beneath the South Pacific[J].Science,1990,248:969-975. |
| [3] | SANS F,RUMMEL R.Geodetic Boundary Value Problems in View of the One Centimeter Geoid.[M].Lecture Notes in Earth Sciences 65,New York Berlin/Heidelberg:Springer,1997. |
| [4] | MILBERT D G.Computing GPS-derived Orthometric Heights with the GEOID90 Geoid Height Model[C]//Technical Papers of the 1991 ACSM-ASPRS Fall Convention,Washington D C:American Congress on Surveying and Mapping,1991. |
| [5] | MILBERT,D G,SCHULTZ D.GEOID.The National Geodetic Survey Geoid Computation Program[R].Silver Spring:Geodetic Services Division,National Geodetic Survey,NOAA,1993. |
| [6] | MILBERT,D G.Improvement of a High Resolution Geoid Height Model in the United States by GPS Height on NAVD 88 Benchmarks[C]//New Geoids in the World:IGES Bulletin:4,Milan:International Geoid Service,1995.13-36. |
| [7] | MILBERT,D G,SMITH D A.Converting GPS Height into NAVD 88 Elevation with the GEOID96 Geoid Height Model[C]//Proceedings of GIS/LIS'96 Annual Conference,Washington D C:American Congress on Surveying and Mapping,1996:681-692. |
| [8] | SMITH D A,MILBERT D G.The GEOID96 High-resolution Geoid Height Model for the United States[J].Journal of Geodesy,1999,73(5):219-236. |
| [9] | SMITH D A,ROMAN D R.GEOID99 and G99SSS:One Arc-minute Models for the United States[J].Journal of Geodesy,2001,75:469-490. |
| [10] | ROMAN D R,WANG Y M,HENNING W,et al.Assessment of the New National Geoid Height Model,GEOID03[J].Surveying and Land Information Science,2004,64(3):153-162. |
| [11] | WANG Y M,SALEH J,LI X,et.al.The US Gravimetric Geoid of 2009(USGG2009):Model Development of Evaluation[J].Journal of Geodesy,2012,86(3):165-180. |
| [12] | ROMAN D R,SMITH D,CHILDERS V A.New Datums by the End of the Next Decade for the United States of America[C]//Proceedings of Society of Exploration Geophysicists Annual Meeting,Denver:[s.n.],2010. |
| [13] | MARTINEC Z,MATYSKA C,GRAFAREND E W,et.al.On Helmert's Second Condensation Technique[J].Manuscr Geod,1993,19:213-219. |
| [14] | MARTINEC Z.Stability Investigations of a Discrete Downward Continuation Problem for Geoid Determination in the Canadian Rocky Mountains[J].Journal of Geodesy,1996,70:805-828. |
| [15] | VANEK P,HUANG J,NOVAK P,et al.Determination of the Boundary Values for the Stokes-Helmert Problem[J].Journal of Geodesy,1999,73:180-192. |
| [16] | HUANG J,SIDERIS M G,VANCEK P,et al.Numerical Investigation of Downward Continuation Techniques for Gravity Anomalies[J].Bolletino Di Geodesia E Scienze Affini LXII,2003(1):33-48 |
| [17] | HUANG J,VRONNEAU M,PAGIATAKIS S D.On the Ellipsoidal Correction to the Spherical Stokes Solution of the Gravimetric Geoid[J].Journal of Geodesy,2003b,77:171-181. |
| [18] | VRONNEAU M,HUANG J.The Canadian Gravimetric Geoid Model 2005(CGG2005) [EB/OL].[2007-02-22]. |
| [19] | NING Jinsheng,LI Jiancheng,CHAO Dingbo,GUAN Zelin.The Research of the Earth's Gravity Field Model WDM94 Complete to Degree 360[J].Journal of Wuhan Technical University of Surveying and Mapping,1994,19(4):280-290.(宁津生,李建成,晁定波,管泽霖.WDM94 360阶地球重力场模型研究[J].武汉测绘科技大学学报,1994,19(4):280-290.) |
| [20] | GUAN Zelin,LI Jiancheng,CHAO Dingbo,et al.The Research of Gravity Geoid WZD94 in China[J].Journal of Wuhan Technical University of Surveying and Mapping,1994,19(4):292-297.(管泽霖,李建成,晁定波,等.WZD94中国重力大地水准面研究[J].武汉测绘科技大学学报,1994,19(4):292-297.) |
| [21] | LI Jiancheng,CHEN Junyong,NING Jinsheng,et al.The Theory of Earth's Gravity Field Approximation and Determination of the China Guasi-Geoid 2000.Wuhan:Wuhan University Press,2003.(李建成,陈俊勇,宁津生,等.地球重力场逼近理论与中国2000似大地水准面的确定[M].武汉:武汉大学出版社,2003.) |
| [22] | MARTINEC Z.Boundary-value Problems for Gravimetric Determination of a Precise Geoid[C]//Lecture Notes in Earth Sciences 73.New York Berlin/Heidelberg:Springer,1998. |
| [23] | HEISKANEN W A,MORITZ H.Physical Geodesy[M].San Francisco/London:Freeman&Company,1967. |
| [24] | SMITH,W H F,WESSEL P.Gridding with Continuous Curvature Splines in Tension[J],Geophysics,1990,55,293-305. |