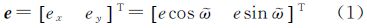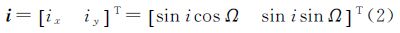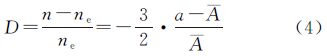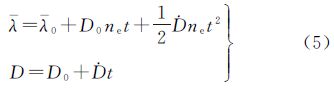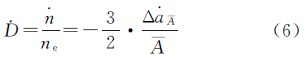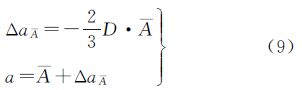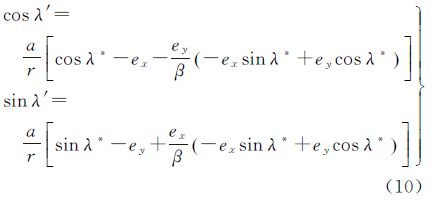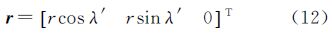2. 北京环球信息应用开发中心,北京 100094
2. Beijing Global Information Application and Development Center,Beijing 100094,China
1 引 言
我国的卫星导航星座中，GEO卫星受自然摄动的影响，必须定期进行东西和南北保持控制以实现相对地球的定点保持[1, 2]。由于机动推力的建模精度不高，制约了长弧动力学定轨的精度[3, 4]。目前的应对策略是机动期间以及机动后数小时恢复期内采用几何法定轨[5]，恢复后则重新启动动力学定轨[6]。通常短期东西机动持续20～30 min，但是在定轨策略控制中为每次机动期均预留2 h。若运控系统能够利用其测轨数据对机动过程进行准确可靠的实时监视，则可以快速固定实际机动期从而缩短定轨策略的交替时段，并可增强运控系统自身的完整性和自洽性。
GEO卫星机动检测方法有几何法和动力学法两种。目前主要采用前者，最简单的是基于站星间视向速度曲线的变化[7]，其次是基于几何法轨道的GEO卫星异常识别[8]，这两种方法常见于大机动推力条件下的变轨识别和变轨时刻判定。对于GEO卫星，由于机动采用间歇式脉冲小推力，且GEO卫星具有静地特性，卫星在地固系下的速度和位置向量以及相对测站的视向多普勒变化均表现为慢渐变性，这给基于时间序列的异常值检测带来一定困难，如检测参数的阈值需要人为设定且多来自于经验。此外，上述两种方法都高度依赖于测轨跟踪数据的质量和采样率或者测站的个数，并且不能反映轨道机动期间的动力学特性。本文基于动力学法监测变轨过程，对机动推力采取平均化思想进行建模，并将东西向加速度与轨道参数合并为七参数集，进行滑动开窗求解。
针对GEO卫星的星下点运动特性和东西机动的工作模式，本文提出了一种基于同步根数的星下点运动轨迹拟合算法。首先，以10 min为计算窗口，利用至少两个地面站的C波段转发式测距跟踪数据，拟合星下点运动的七参数集；其次，分别从滑动开窗的拟合轨道根数变化和拟合-预报的测距残差两个方面出发，对机动进行一致性判别。东西机动实测数据处理表明该方法取得了良好的数据拟合效果，能够有效监视东西机动。与其他方法相比，提高了检测和识别的可靠性，并且降低了对测站及其数据的依赖程度。
2 基于同步根数的短期星下点运动 2.1 同步根数
卫星在惯性系下的轨道运动常用开普勒根数描述，即以a、e、i、Ω、ω、M分别表示轨道半长轴、偏心率、轨道倾角、升交点赤经、近点角距和平近点角。
为便于反映GEO星下点在其定点经度附近的运动特性，常使用地固系下的6个同步根数σe={e,i,λ,D}[1]。其中二维偏心率矢量e和倾角矢量i分别为
式中，ω=ω+Ω；瞬时平经度定义为
λ=ω+M为平赤经，θg表示Greenwich平恒星时，由于吸收了地球平均自转效应，λ反映了星下点的运动特征。需要强调的是，平经度λ和平赤经λ均是沿轨道面计量的，仅当轨道倾角为零时，才对应严格意义上的地理经度和赤经含义。
由开普勒第三定律，平经度漂移率D定义为
式中，ne为地球自转平均角速率；A为静止轨道半长轴。在摄动作用下，静止轨道半长轴并非二体问题下的标准静止轨道半长轴A，而是满足
得到的计算值[1]。
平经度漂移率D反映了卫星相对于定点经度的漂移速率。注意到D与轨道高差的反向关系，若卫星圆轨道比静止轨道高(a>A)，则轨道周期比恒星日长，其运动将落后于地球自转，导致平经度向西漂移(D＜0)；反之亦然。当漂移率D≠0，即使不考虑摄动因素，平经度λ也存在东西向漂移。
2.2 根数摄动分析在各种摄动因素作用下，瞬时同步根数的变化有长期项和各种周期项，如地球引力位J2引起的半周日周期项和轨道共振(J22为主项)引起平经度λ的长周期漂移等[1]。而轨道共振的力学机制是GEO卫星频繁定点机动的根本原因[9]。
短时段内，平经度λ的长周期漂移可以处理为常加速度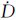
作用下的加速漂移。对于我国境内上空的GEO环带(80°E-160°E)，环带卫星均具有向西的漂移加速度，且加速度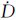的大小与定点经度有关。
因此，考虑10 min内GEO的摄动主项，星下点运动轨迹的描述参数选取为6个同步根数和1个长期摄动项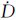。其中，摄动参数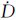主要吸收J22等引起的轨道东西沿迹向的长期定点漂移，同时也能吸收周期项的短期累积部分。
在漂移加速度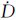的作用下，平经度及其漂移率的变化分别表现为抛物线和线性漂移形式[1, 2]，即
式中，λ0和D0分别为初始时刻的平经度和漂移率。
以某西漂卫星为例，令初始时刻卫星定点在漂移所允许的窗口西边界λ0，同时轨道高度低于静止轨道以使得D0>0。在自然摄动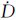＜0的作用下，漂移率D将持续减小至零，继而变为负值，即从D0减至-D0，由式(4)可知，轨道则是持续升高并超过静止轨道高度；平经度λ则是沿开口向下的抛物线首先减速东漂至东边界，继而反向加速漂回西边界。此时需要实施机动，降低轨道高度将D从-D0恢复到D0，随后开始新一轮的抛物线运动直至下一次机动。
因此，定期的东西定点机动是为了抑制平经度的长期漂移。其实质是通过调节漂移率D(即轨道高度)以达到利用反向的线性漂移抑制自然摄动引起的加速漂移。
若利用机动推力持续改变轨道高度的过程是一个较平稳过程，可以将处理为常值。由式(4)可得
式中，
为半长轴的变化率。显然，机动窗口内持续小推力作用下，有与非机动期不一致的漂移加速度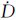，但是，七参数仍适于描述机动期内的星下点运动。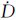等效于，反过来也可以根据的累积变化幅度ΔaA判断机动的发生。
因为机动段通常无法获得精密轨道，首先利用非机动段的动力学轨道对七参数的星下点运动拟合精度进行评估。下面推导出七参数模型与地固系卫星位置向量的函数关系，其思路是利用第二类无奇点根数作为中间转换参数，首先在惯性系进行严密卫星位置计算，再旋转回到地固系的卫星位置。
3.1 GEO卫星的地固系位置计算在轨道上新建一个拟春分点，使得拟春分点至升交点的角距为Ω。定义轨道坐标系O-pqw：原点O为地球质心；Op轴指向拟春分点方向；Ow轴沿轨道角动量方向;Oq轴由右手法则确定。
轨道坐标系与地心惯性系的转换矩阵为M=Rz(-Ω)Rx(-i)Rz(Ω)，将式(2)代入，有
式中，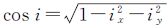
。
令θg0为历元时刻toe的Greenwich平恒星时，由历元时刻的拟合参数{D0,e,i,λ0,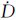},计算t=t-toe时刻位置的流程如下：
(1) 由式(5)计算平经度λ和漂移率D。
(2) 由式(3)和式(4)计算平赤经λ和半长轴a
(3) 按照广义开普勒方程
λ*-exsinλ*+eycosλ*=λ
以及偏赤经与真赤经间的转换公式
计算偏赤经λ*和真赤经λ′，式中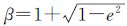
。
(4) 计算向径r
(5) 计算轨道坐标系中的位置向量r
(6) 旋转至地固系下的位置向量R
需要说明的是，前两步进行了同步根数的时间传播，并转换为第二类无奇点根数{a,e,i,λ}；中间步骤是严格的卫星星历计算；最后一步中，惯性系与地固系的转换忽略了岁差章动和极移改正项，仅考虑地球自转的一阶效应，因此需要较为准确的Greenwich平恒星时。
3.2 星下点运动的拟合精度检验分别选取定点在140°E和84°E附近的两个GEO卫星的1 d地固系位置向量数据，采样率为1 s，每10 min拟合一组七参数，共计144组。
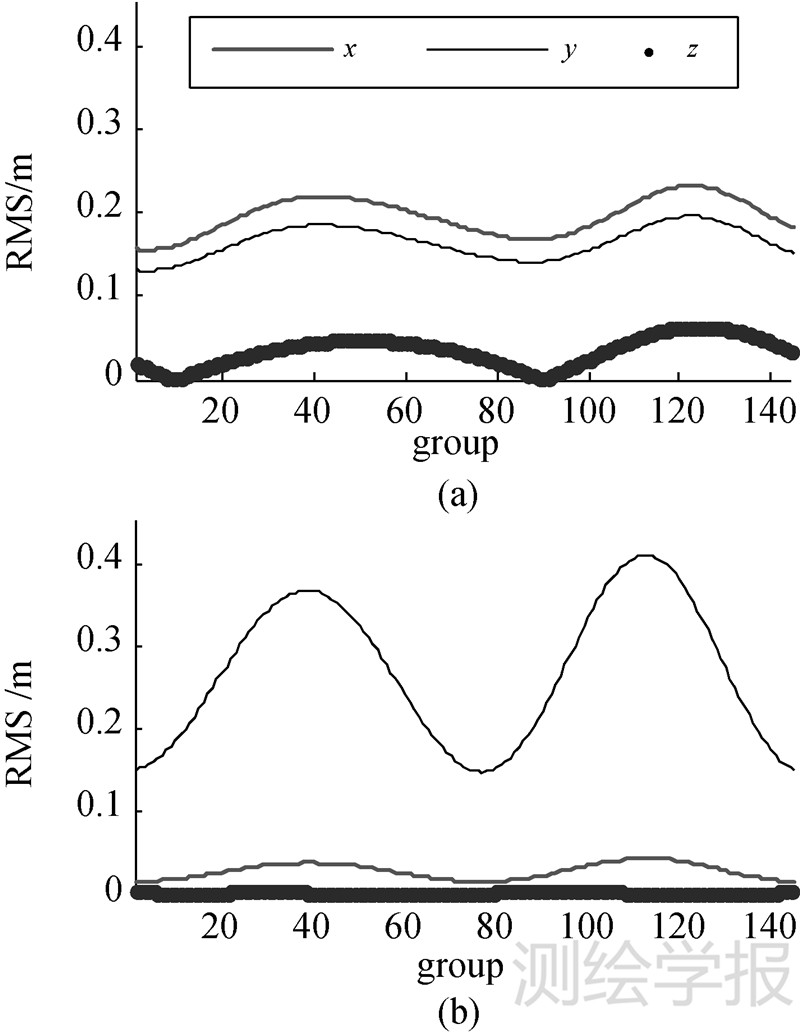
图 1分别给出了两卫星在地固系X、Y、Z位置三分量上的残差均方根(root mean square,RMS)序列。可以看出，利用七参数模型描述10 min内的星下点运动是可行的，拟合精度优于0.5 m。此外，序列明显具有半周日周期波动性，表明短期拟合无法吸收的周期摄动项依然存在。
|
| 图 1 七参数模型对140°E(a)和84°E(b)卫星位置拟合的RMS序列 Fig. 1 RMS series of 140°E and 84°E as fitted by 7-parameter model |
C波段转发式测距是目前运控系统常用的GEO 卫星测轨技术手段之一。转发式测距是双程测距模式，跟踪站测距信号经卫星转发器转发后被地面接收，因此观测值中不包含卫星钟差和接收机钟差信息，其具体工作流程和测量模型参见文献[10, 11, 12, 13, 14, 15, 16]。
由两个或两个以上转发式测距站的10 min跟踪数据拟合求解窗口内星下点运动七参数，进而计算出一组开普勒根数和拟合-预报段测距残差[16]。其实质是一种地固系下的运动学定轨，且对机动段和非机动段同样适用。由于拟合结果体现了10 min内的累积和平均化信息，更便于反映持续的间断小推力的作用效果。
对于东西机动，小推力的累积变化主要是改变平经度漂移加速度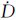，即持续地降低或抬高轨道高度，因此，基于拟合半长轴变化ΔaA的窗口序列是基本的机动监视参数。
此外，漂移加速度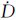的改变使得进出机动窗口时，均会影响各站的下一组预报段测距残差。因此，拟合-预报段测距残差的RMS窗口序列也是机动监视参数之一，在卫星发生轨控或出现异常状况时能够提供较为可靠的一致性验证信息。
利用2011年9月13日我国北京、三亚、喀什和成都4个转发测距站的自发自收测距数据计算某GEO卫星的机动监视参数的移动窗口序列，数据采样率为1 s，东西机动标定时段为UTC时间4-6 h。
为便于实时机动监视，对原始观测数据的预处理要求尽量简单。这里仅利用前一天的标定值对跟踪站设备的收发时延和卫星的转发器时延进行改正，同时利用SAAS模型进行对流层延迟改正。此外，计算Greenwich平恒星时需要UTC-UT1改正，采用IERS公布的预报值。测距站的坐标系为ITRF2000，静止轨道半长轴A取为42 165 760 m[1]。
为适应更宽的GEO环带和可能发生的测站故障，并考察机动判断响应时间，设计以下3种机动监视方案：
(1) 三站10 min拟合-预报窗口。
(2) 两站10 min拟合-预报窗口。
(3) 三站5 min拟合-预报窗口。
5.1 方案1为便于客观评定监视效果，利用前3个站的1 d转发测距数据，以10 min为单位，划分出144组拟合窗口。首先滑动拟合出每个窗口的轨迹七参数，进而计算出每个窗口的轨道根数、三站的拟合-预报残差的RMS。然后，将拟合结果用于成都站的测距预报，其预报残差的统计也一并列出。
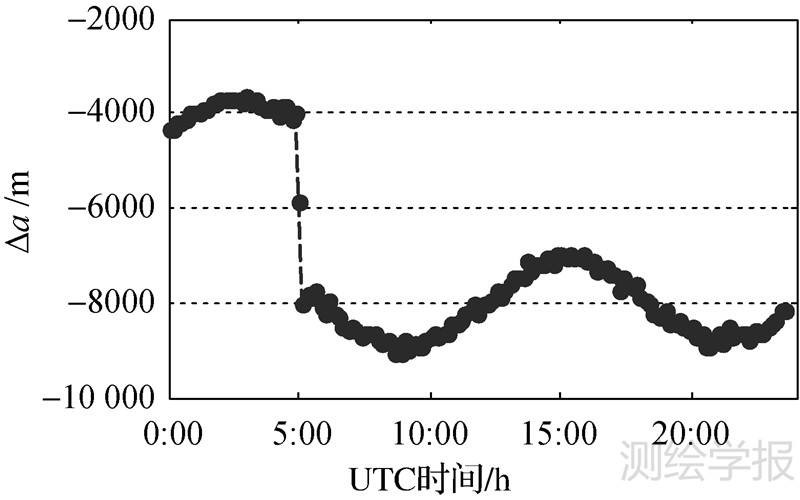
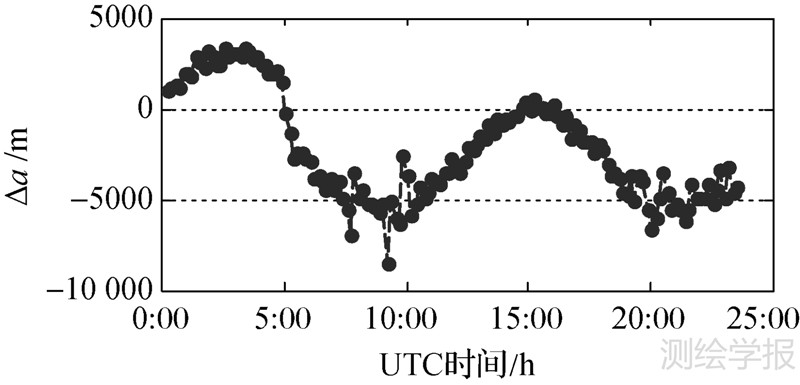
图 2为当天的144组拟合半长轴的窗口序列(统一与A做差)。其中4∶50-5∶00和5∶00-5∶10(UTC)出现两组连续的大幅下滑，表明此处即为短期东西机动，其实际点火时段集中在4∶50-5∶10，持续20 min左右，轨道下降约4 km。这与事后的轨控和遥测报告中的实际点火窗口基本一致。
|
| 图 2 拟合半长轴的窗口序列 Fig. 2 Series of the fitted semi-major axis |
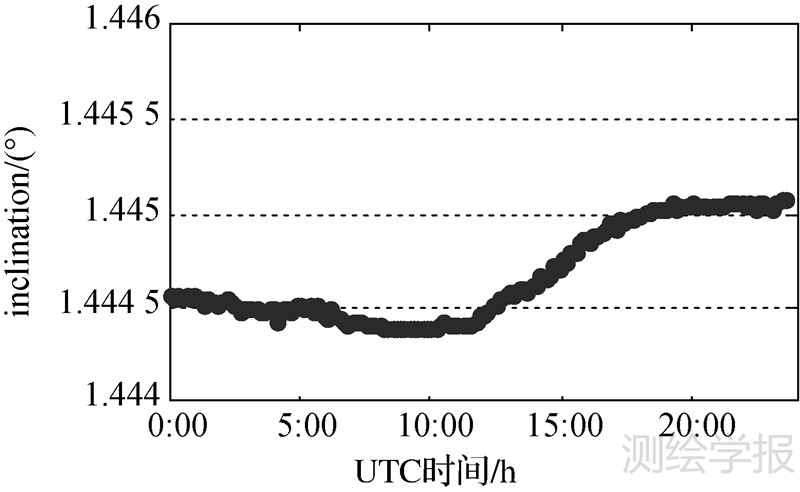
为区别于南北定点机动，列出轨道倾角的拟合序列，如图 3所示。显然，东西机动为共面变轨，对倾角拟合值基本不影响。
|
| 图 3 拟合轨道倾角的窗口序列 Fig. 3 Series of the fitted inclination |
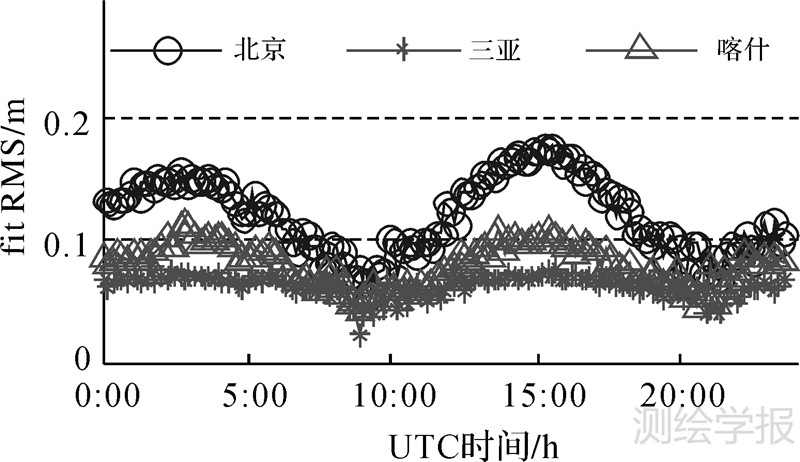
图 4列出了三站的拟合残差RMS序列，拟合精度优于0.2 m，其中三亚站较好，在0.1 m水平。值得注意的是，即使在机动变轨段，各站数据的拟合残差并无异常，表明七参数模型能够同时适用于机动和非机动的窗口拟合。
|
| 图 4 三站拟合残差RMS的窗口序列 Fig. 4 RMS series of fitted(O-C)of 3 stations |
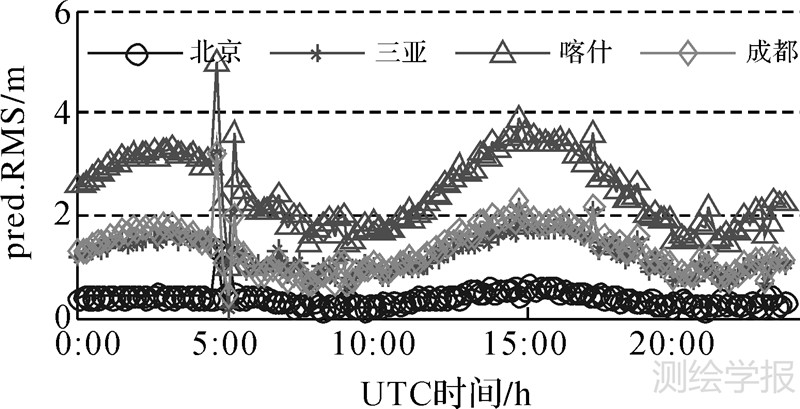
图 5是包括成都站在内的测距预报残差RMS序列。其中预报精度以北京站最好，优于1 m，三亚与成都相当，在2 m以内，喀什站则为4 m。由于轨道误差对测距的影响体现在视线方向上，该星定点在140°E附近，与北京站经差最小，与喀什站经差最大，而拟合预报的卫星误差通常在沿迹(即东西向)最差，对喀什站的视线投影影响最显著。
|
| 图 5 4站预报残差RMS的窗口序列 Fig. 5 RMS series of predicted(O-C)of 4 stations |
图 5中还可明显看到，5 h左右的东西机动窗口处，每站的预报残差RMS序列均出现两个较大幅度的预报异常值，这是进出机动窗口力模型不一致的应有表现。
此外，即使存在机动，半长轴序列和拟合-预报残差RMS序列均有一致的半周日周期波动，表明4站当天的数据质量以及拟合的内符合较好。但是，拟合的外符精度不高，残差预报精度比拟合精度放大10～40倍，表明数据预处理和建模等仍有改进余地。
5.2 方案2
仅采用北京和三亚两个测距站数据进行监视计算。结果表明，若结合已知的2 h机动时段规划，半长轴的变化序列和两站的预报残差RMS序列仍能一致地敏感到机动过程(图 6与图 7(b))。与图 2相比，图 6的半长轴变化规律性一致，但整体抬高超过4 km；表明两站组合的观测几何较弱，虽然能够保证七参数拟合中(与关联)的精度，但是对D0(与ΔaA关联)的估计精度不高。
|
| 图 6 两站拟合半长轴的窗口序列 Fig. 6 Series of the fitted semi-major axis using data of 2 stations |
|
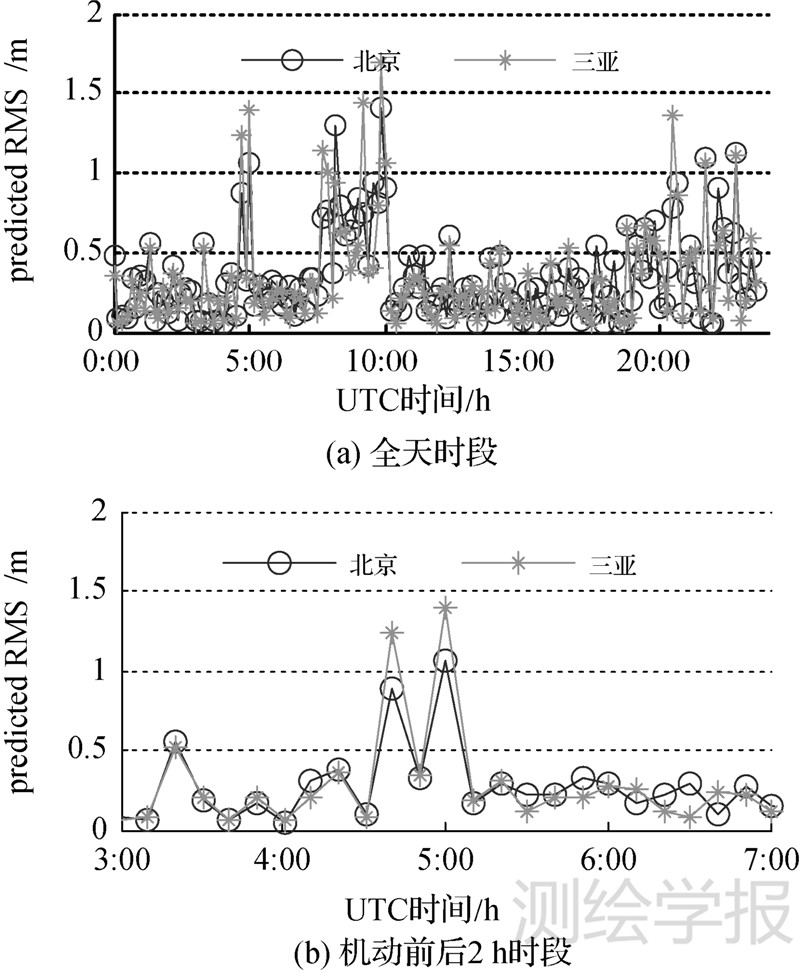
| 图 7 两站的预报残差RMS Fig. 7 RMS of predicted(O-C)of 2 stations |
图 7(b)放大了机动标定时段4-6 h附近的4 h预报窗口情况。注意到20 min的点火过程被分配到两个拟合窗口，除了进出实际点火窗口时出现合理的预报异常外，在两个异常值中间的预报值是正常的，且两站的一致性很好，这正是利用前10 min点火段的拟合轨道预报后10 min点火段的测轨跟踪，表明将机动小推力的持续作用处理为平稳加速过程是合理的，七参数模型对机动段也具有较好的短期预报能力。此外，也表明10 min窗口大小的设置对拟合和预报均是合理适用的。
采用北京和喀什的两站组合监视也有基本一致的结果，但是与三站组合相比，两站组合对数据质量和观测几何的敏感性增强，参数解算精度有所下降，对实际机动时段的准确判断带来一定影响。此外，除了对机动作出正确反映，容易受数据质量波动产生不明跳变。
5.3 方案3仍采用方案1的三站数据，将拟合和预报窗口由10 min缩短到5 min，目的在于考察机动监视的快速判断和响应时间。
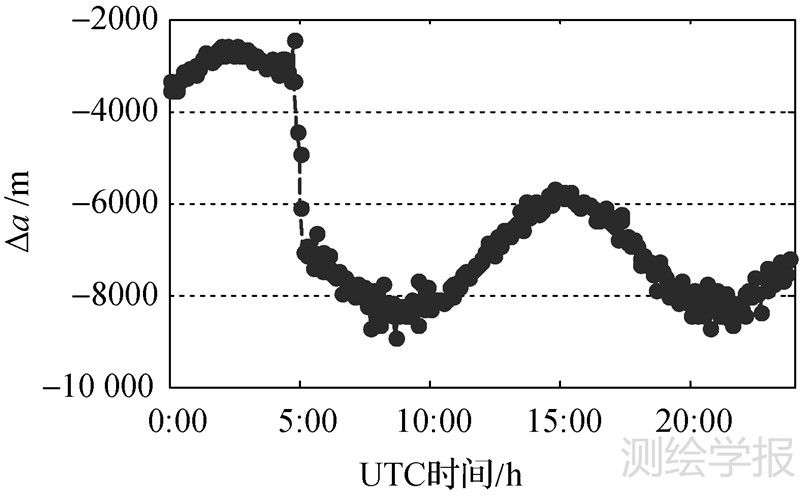
图 8是拟合半长轴变化序列，能够及时监视到5 h附近的短期东西机动，与方案1的10 min拟合窗口(见图 2)相比，有较好的一致性，其中点火段被分配到4个拟合窗口，数据有整体抬高，且抖动性有所变大，但是仍比方案2的图 6效果好。由于预报窗口仅有5 min，预报残差RMS序列没有出现明显跳跃点，不能一致性地敏感到机动时段，故略去数据图。
|
| 图 8 方案3的拟合半长轴窗口序列 Fig. 8 Series of the fitted semi-major axis using data of scheme 3 |
GEO卫星的定点机动是卫星测控系统的常管工作，与地面运控系统相分离。但是运控系统可以利用其高精度高采样率的测轨数据进行实时监视，这将增强系统自洽性，并有利于总结和改善机动建模工作以实现包含机动段的长弧动力学定轨。
(1) 基于同步根数和定点漂移运动规律，提出描述短期GEO星下点运动的七参数模型。与常规开普勒拟合参数相比[18, 19, 20]，具有无奇点和同时适用于机动和非机动的特点。
(2) 基于东西定点机动的工作原理，提出拟合半长轴窗口序列和测站测距拟合-预报残差RMS窗口序列的机动监视方法。与直接基于时间序列的异常检测方法相比，开窗法延缓了响应时间，但便于累积持续小推力作用效果，使得判别更加灵敏和可靠。
(3) 合理布设的C波段转发式测距站的三站10 min测轨跟踪数据能够稳定地反映机动点火时段。在特殊情况下，减少测轨站或缩短拟合窗口也可以快速响应机动过程。
本文方法已对不同GEO卫星的多次东西机动进行了监视，可靠性高。由于C波段转发式测距站较少，下一步可以采用北斗基准站网的伪距相位数据监视机动过程。此外，与东西定点机动相比，南北机动虽然频率低得多，其机动监视仍有意义，需要进一步验证七参数模型和机动检测方法对其的适用性。
| [1] | LI Hengnian. Geostationary Satellite Orbital Analysis and Collocation Strategies[M]. Beijing: National Defense Industry Press, 2010. (李恒年. 地球静止卫星轨道与共位控制技术[M].北京:国防工业出版社,2010.) |
| [2] | SOOP E M. Handbook of Geostationary Orbits[M]. Beijing: National Defense Industry Press, 1999. (Soop E M. 地球静止轨道手册[M].北京:国防工业出版社,1999.) |
| [3] | SONG Xiaoyong, JIA Xiaolin, JIAO Wenhai, et al. Determining Maneuver Orbit of GEO Using Stochastic Thrust Model[J]. Geomatics and Information Science of Wuhan University, 2009,34(5):573-576. (宋小勇,贾小林,焦文海,等. 基于随机姿控力模型的GEO卫星机动定轨[J]. 武汉大学学报:信息科学版,2009,34(5):573-576.) |
| [4] | HUANG Yong, HU Xiaogong, HUANG Cheng, et al. Precise Orbit Determination of a Maneuvered GEO Satellite Using CAPS Ranging Data[J]. Science in China: Physics, Mechanics and Astronomy,2009,52(3): 346-352. |
| [5] | GUO Rui,ZHOU Jianhua, HU Xiaogong, et al. A New Strategy of Rapid Orbit Recovery for the Geostationary Satellite [J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(Supplement): 19-25.(郭睿,周建华,胡小工,等. 一种地球静止轨道卫星的快速恢复定轨方法[J].测绘学报,2011,40(S0): 19-25.) |
| [6] | YANG Xuhai, LI Zhigang, FENG Chugang, et al. Methods of Rapid Orbit Forecasting after Maneuvers for geostationary Satellites[J].Science in China: Physics, Mechanics and Astronomy,2009,52(3):333-338. |
| [7] | HUA Aihui, YANG Xuhai, WANG Xiaohan. A Method to Monitor Geostationary Satellite Maneuver Based on Orbit Measuring System with Transponder[J]. Journal of Time and Frequency. 2007,30(2):118-124. (华爱辉, 杨旭海,王晓晗.基于转发式测轨系统的GEO卫星机动检测初探[J].时间频率学报,2007,30(2):118-124.) |
| [8] | LIU Yanyu, CHANG Zhiqiao, HE Feng, et al. GEO Satellite Abnormity Recognition Based on Wavelet Analysis[J]. Journal of Geodesy and Geodynamics,2010, 30(5):73-76. (刘雁雨, 常志巧, 何峰, 等.基于小波分析的GEO卫星异常识别研究[J].大地测量与地球动力学,2010, 30(5):73-76.) |
| [9] | LIU Lin, HU Songjie, WANG Xin. An Introduction of Astrodynamics[M]. Nanjing: Nanjing University Press, 2006.(刘林, 胡松杰, 王歆.航天动力学引论[M].南京:南京大学出版社,2006.) |
| [10] | LI Zhigang, YANG Xuhai, AI Guoxiang, et al. A New Method for Determination of Satellite Orbits by Transfer[J].Science in China: Physics, Mechanics and Astronomy,2009,52(3):384-392. |
| [11] | YANG Ying, LI Zhigang, YANG Xuhai, et al. Satellite Orbit Determination by Transfer with Differenced Ranges[J].Chinese Science Bulletin, 2012,57(36):4701-4706. |
| [12] | LEI Hui, LI Zhigang, YANG Xuhai, et al. Geostationary Orbit Determination Using SATRE[J]. Advances in Space Research,2011,48(5):923-932. |
| [13] | GUO Rui, HU Xiaogong,Tang Bo, et al. Precise Orbit Determination for Geostationary Satellites with Multiple Tracking Techniques[J]. Chinese Science Bulletin, 2010, 55(8): 687-692. |
| [14] | LEI Hui, LI Zhigang, YANG Xuhai, et al. Precise Orbit Determination Experiment of COMPASS-GEO Based on Transponder Ranging[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(Supplement):31-33.(雷辉,李志刚,杨旭海,等. 基于转发式的北斗卫星导航系统地球静止轨道卫星精密定轨试验[J]. 测绘学报, 2011, 40(S0): 31-33.) |
| [15] | GUO Rui, HU Xiaogong, LIU Li, et al.Orbit Determination for Geostationary Satellites with the Combination of Transfer Ranging and Pseudorange data[J].Science in China: Physics, Mechanics and Astronomy,2010,53(9):1746-1754. |
| [16] | HUANG Yong, HU Xiaogong, ZHANG Xiuzhong, et al.Improvement of Orbit Determination for Geostationary Satellites with VLBI Tracking[J].Chinese Science Bulletin,2011,56(26):2765-2772. |
| [17] | TAPLEY B D, SCHUTZ B E, BORN G H. Statistical Orbit Determination [M].[S.l.]:Elsevier Academic Press, 2004. |
| [18] | HE Feng, WANG Gang, LIU Li, et al. Ephemeris Fitting and Experiments Analysis of GEO Satellite[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(Supplement): 52-58. (何峰,王刚,刘利,等.地球静止轨道卫星广播星历参数拟合与试验分析[J]. 测绘学报,2011,40(增刊):52-58.) |
| [19] | CHEN Liucheng, HAN Chunhao, CHEN Jinping. The Research of Satellites Broadcast Ephemeris Parameters Fitting Arithmetic [J]. Science of Surveying and Mapping, 2007,32(3):12-14.(陈刘成,韩春好,陈金平.广播星历参数拟合算法研究[J]. 测绘科学,2007,32(3):12-14.) |
| [20] | HUANG Yong, HU Xiaogong, WANG Xiaoya, et al. Precision Analysis of Broadcast Ephemeris for Medium and High Orbit Satellite [J]. Progress in Astronomy, 2006,24(1):81-87.(黄勇,胡小工,王小亚,等.中高轨卫星广播星历精度分析[J];天文学进展,2006,24:81-87.) |