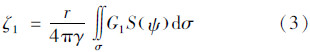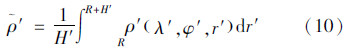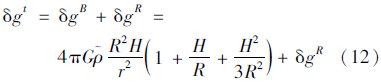1 引言
近岸陆地地形起伏对近海海域高程异常有贡献,海岸带似大地水准面理应在Molodensky框架中解算。研究合适的重力似大地水准面确定算法,是海岸带似大地水准面能否达到厘米级精度水平的重要基础。
尽可能多地集成多源地面重力、航空重力、海洋重力和卫星测高数据,是提高海岸带重力场和大地水准面精化水平的基本途径。通常,海岸带范围内重力场数据来源复杂,研究分析这些数据所采用的大地测量基准是否一致以及对重力场和大地水准面精化的影响规律,对有效实现多源重力场的数据集成相当重要。
传统的地形归算方法仅适合地球表面上的重力异常和扰动重力,不适合其他类型重力场参数,不能用于航空重力、卫星重力、浅水卫星测高垂线偏差等重力场数据处理。厘米级大地水准面精化对地形影响处理技术提出了更高要求,研究适合厘米级精度的地形影响算法,也是海岸带大地水准面能否实现厘米级精度目标的关键因素之一。 2 似大地水准面应在Molodensky框架中计算
沿海地区有一定的地形起伏,Molodensky一阶项G1(受地形起伏大小影响,与地面高程绝对大小关系不大)在近岸地区不为零,将G1项进行Stokes积分后对近海似大地水准面有贡献。实际上,似大地水准面在陆海交界处不可能突然变成与大地水准面重合,而是经过近岸海域一定区域的平滑而解析地过渡,逐渐趋近于大地水准面。图 1是直接采用线性Molodensky公式按FFT快速算法得到的海岸带区域Molodensky一阶项及其对似大地水准面的贡献。计算表明,在我国海岸带,Molodensky一阶项对似大地水准面的贡献在10 cm左右,部分地区超过20 cm。整个台湾海峡(不含台湾本岛),Molodensky一阶项对似大地水准面的贡献在15~30 cm。可见,在我国海岸带,要想实现厘米级精度的似大地水准面,离岸距离在100 km范围内的海域都应严格在Molodensky框架中处理。

|
| 图 1 海岸带区域Molodensky一阶项(上图)及其对高程异常的贡献(下图) Fig. 1 Molodensky I and its contribution to height anomaly in coastal region |
Molodensky理论框架的边界面为地球表面,采用不同的边界条件,解的形式也不同。下面分别给出以地面上重力异常、扰动重力和垂线偏差为边界条件的3种常见情况下,似大地水准面在线性Molodensky框架内的球近似解,取至一阶项。 2.1 已知地面重力异常Δg
高程异常零阶项ζ0按Stokes公式计算
式中,r为计算点的地心距;σ为单位球面;S(ψ)为Stokes函数;ψ为计算点到积分面元之间的角距。 式中,h为流动点正常高;hp为计算点正常高;γ为计算点的正常重力;l0为计算点与流动点的水平距离。高程异常一阶项ζ1为
地面高程异常(似大地水准面高)为
ζ=ζ0+ζ1 2.2 已知地面扰动重力δg[1]
式中,H(ψ)为Hotine函数。2.3 已知地面垂线偏差
地面高程异常零阶项ζ0为
式中,α为ψ方向上的方位角。
地面重力异常计算公式为
代入式(2)计算一阶项G1,再按Stokes公式计算出ζ1。
通常将利用重力和地形资料,按基于边值问题方法确定的似大地水准面,称为重力似大地水准面。 3 应重视多源重力场数据的相容性问题
在利用多源重力数据精化局部重力场和确定高精度大地水准面时,应重视多源重力数据的大地测量基准一致性问题。 3.1 正常重力计算方法不一致及影响
目前已公布的地球重力场位系数模型会明确该模型对应的正常重力场,但不同机构或部门发布的重力场模型或卫星重力场模型,采用的正常重力场不尽相同。在地面重力数据处理过程中,通常采用规范中Helmert公式计算正常重力,这个正常重力公式与特定的正常椭球一一对应,我国目前采用GRS1980正常椭球,长半轴a=6 378 137 m,与EGM2008重力场模型中正常椭球的长半轴a=6 378 136.3 m不同。
图 2为两种正常椭球算得的正常重力之间的差异(大小为5.7~6.5 mGal,图中高频成分为Helmert正常重力公式与正常重力球谐表达式之间的差别)。采用不同椭球的正常重力来表示扰动重力、空间异常等扰动重力场参数,它们的差别主要表现为系统性的低频误差。

|
| 图 2 GRS1980正常重力与EGM2008重力场模型正常重力的差别 Fig. 2 The difference between GRS1980 normal gravity and EGM2008 normal gravity |
对于同一计算区域,若地面重力数据和参考重力场模型对应的正常重力不一致,甚至不同来源的地面重力数据采用的正常重力公式也不严格一致,情况将变得异常复杂。这种情况在综合历史重力数据中几乎不可避免。对精化重力场和大地水准面的影响会随数据处理算法的不同而变化,使得误差影响变得不可预测和控制。
因此,在多源重力场数据处理和大地水准面精化过程中,应保证不同来源的重力场数据所参考的正常重力场及其计算公式保持一致。在没有条件保证严格一致的情况下,应利用不同正常重力场下扰动重力场参数之间差别的低频特性,用较好的重力场数据进行标定,通过校正来统一正常重力场。 3.2 潮汐基准不统一的影响
在我国,传统大地测量成果采用无潮汐基准[2]。水准高程(高差)采用无潮汐基准,GPS卫星定位默认采用零潮汐基准,因此,实际得到的离散GPS水准高程异常值存在潮汐基准不统一问题。由海洋卫星测高数据反演的海洋重力场参数所参考的潮汐基准一般认为是平均潮汐基准。
不同潮汐基准对大地测量观测量的影响只与纬度有关,与经度无关,且表现为低频性质。例如,将GPS大地高从零潮汐基准转换为无潮汐基准时,在纬度10°~60°区域所需增加的改正数为0.25~6.80 cm;将卫星测高海面高从平均潮汐基准转换为无潮汐基准时,在纬度10°~60°区域所需增加的改正数为-0.6~-15.5 cm。 3.3 区域性高程基准的问题
在地球重力场理论中,高程基准是指全球高程基准,即大地水准面对应的大地位或正常椭球面对应的正常位。因此,计算空间重力异常中正常重力采用的高程基准应该是全球高程基准,而不能是区域性高程基准。但在实际地面空间异常计算时,常用区域性高程基准代替全球高程基准,会给空间异常引入系统性误差。
潮汐基准不同、区域性高程基准使用对重力场大地水准面影响特性与正常重力场不一致的影响类似,解决的办法也基本相同。在多源重力场数据处理和大地水准面精化过程中,应保证不同来源的重力场数据所参考的潮汐基准一致,高程基准是全球高程基准,区域性高程基准差别也应事先标定或迭代计算,否则也会导致误差影响变得不可预测和控制。 4 采用地形影响移去恢复法提升重力数据处理水平
将地球外空间各类重力场参数的地形影响定义为地形质量生成的同类型重力场参数的大小。显然引力位(扰动位)的地形影响在地球外空间是调和的。
地球重力场理论指出,地球外空间任意类型扰动重力场参数都可以表示为同一高度上扰动位、扰动重力或其对位置偏导数的线性组合。因此,若解决了扰动位和扰动重力的地形影响问题,其他类型重力场参数的地形影响问题也就迎刃而解。
对于任意类型地球重力场参数,本文中的“地球外空间”泛指包括地面、海面、低空和卫星高度。 4.1 球近似下地形影响算法
下面给出球近似下地球外空间任意类型重力场参数的地形影响球近似算法[3]。 4.1.1 扰动位的地形影响计算
在球近似下,扰动位的地形影响可表示为
式中,G为万有引力常数;H为地球外空间计算点正下方的地形高程;r为计算点的地心距;TB称为扰动位的球壳布格改正。
式中,ρ′为流动点的地形等效密度,即地面到大地水准面之间地形的几何平均密度;r′,λ′,φ′为流动点的球坐标;H′为流动点的地形高程。
在局部地形影响计算中,仅需考虑地表密度ρ,扰动位的局部地形影响可表示为
式中,r,λ,φ为计算点的球坐标; L-1为牛顿积分核函数(即流动点到计算点空间距离L的倒数)。 4.1.2 扰动重力的地形影响计算在球近似下,扰动重力的地形影响δgt可表示为
式中,δgB称为扰动重力的球壳布格改正。根据定义,扰动重力的局部地形影响可表示为
4.2 地形影响的移去恢复法
在地球外空间,地球引力场本身是调和的,引力位的地形影响也是调和的。也就是说,实际地球重力场参数之间的解析关系式完全适用于地形影响。
因此,只要有了数字地形模型及相关数据,就可以计算地球外空间任意高度不同类型重力场参数的地形影响,重力场参数类型可以是高程异常、重力异常、扰动重力、垂线偏差或重力梯度等,甚至是卫星跟踪卫星观测量,适合区域可以是陆地、陆海交界和海洋区域,高度可以是地球外空间任意高度。图 3为直接用于计算(局部)地形影响的一种计算方案。

|
| 图 3 地球外空间重力场参数地形影响计算方案 Fig. 3 Computation scheme of the terrain effects on the gravity parameters in Earth’s outer space |
例如,地球外空间(r=R+H)重力异常的地形影响可由重力异常定义直接给出

同理,已知扰动位地形影响,垂线偏差地形影响也可由定义直接给出。
再如,已知扰动重力地形影响,则高程异常地形影响可由Hotine积分公式直接计算。
移去-“重力场参数解析关系式”-恢复法应满足的条件是:移去量与恢复量对应的引力场均是调和的,且移去量与恢复量之间的关系符合“重力场参数解析关系式”。
海岸带重力场数据集成的目标可概括为:利用不同高度上的多源重力场数据,如陆地地面重力、海洋船测重力、航空重力、卫星测高等数据,结合数字地形模型,估计地面某种类型的平均重力场参数(重力异常、垂线偏差或扰动重力等)。
重力场数据集成涉及重力场延拓、拼接、融合和格网化问题,延拓是将不同高度的重力场参数解析延拓到地球表面;拼接主要解决两个及两个以上完全不重叠和不交叉数据源的集成问题;融合主要解决一个区域存在两个及两个以上重叠或交叉数据源的集成问题。
如同参考重力场移去恢复法分离地球引力场的中低频分量一样,地形影响移去恢复法的实质是精确分离重力场参数的地形高频分量,即在数据集成前,先移去源重力场参数的地形影响,然后进行数据集成,最后再恢复目标重力场参数的地形影响。
在多源重力场数据处理时,可先移去所有源重力数据的地形影响,对扣除地形影响后的重力数据进行处理,最后,仅需恢复目标数据的地形影响即可。
地形影响的移去恢复法能用于延拓、拼接、融合和格网化等所有重力场数据集成算法,可抑制地形代表性误差,有效抑制重力场数据集成过程中的高频信息损失。因此,从这个意义上说,精确处理地球外空间各种类型重力场参数的地形影响是提升区域多源重力场数据处理水平的重要途径。 5 将Helmert凝聚引入Molodensky框架 5.1 外空间任意类型参数的地形Helmert凝聚
地形的Helmert凝聚(压缩),涉及一种称为地形质量补偿的概念,简称地形补偿。大地水准面外部空间任意类型重力场参数地形补偿的严密定义是:为抵消扣除地形质量(即扣除地形影响)后导致地球引力场发生变化,从而对该类型重力场参数进行的质量补偿量。
地形Helmert凝聚可分解为两个步骤:扣除地形质量生成的引力场,即减去地形影响;补偿扣除地形质量后引起的引力场变化,即加上地形补偿。因此,对于地球外空间任意类型重力场参数χ,地形Helmert凝聚引起的重力场参数变化(称为重力场参数的Helmert凝聚,下同)可表示为
式中,χh为χ的Helmert凝聚;χt为χ的地形影响;χc为χ的地形补偿。
对地形进行Helmert凝聚后的大地水准面外部空间,称为Helmert空间,对应的引力场为Helmert引力场,它是调和的,且与实际地球引力场相差由地形Helmert凝聚引起的引力场变化。因此,地形的Helmert凝聚改变了实际地球引力场。 5.1.1 球近似下地形补偿与Helmert凝聚算法
这里给出大地水准面外部调和空间中,任意高度扰动位和扰动重力地形补偿的球近似算法。
(1) 扰动位的地形补偿为
式中,μ=H1+HR+H23R2称为地形质量补偿密度;H为计算点正下方的地面高程;TcR称为扰动位的局部地形补偿。
(2) 扰动重力地形补偿为
式中,δgcR称为扰动重力的局部地形补偿。
将式(9)和(15),及式(12)和(16)分别代入式(14),就导出了球近似下地球外空间的扰动位Helmert凝聚和扰动重力Helmert凝聚,进而得到其他类型重力场参数的Helmert凝聚。
将图 3中的“地形影响”用“地形补偿”或“Helmert凝聚”替换,就变成了地球外空间地形补偿或Helmert凝聚计算方案。
这样,球近似下地球外空间任意类型重力场参数χ的Helmert凝聚可表示为
由式(17)可以看出,球壳布格改正抵消,也就是说,Helmert凝聚等于局部地形补偿与局部地形影响之差。可见,Helmert凝聚是个比局部地形影响更小的量。 5.1.2 直接地形影响与间接地形影响
在Stokes框架的大地水准面精化中,必需精细处理地形影响,进行重力归算,如地形影响的改正和地形的Helmert凝聚改正,涉及对地面重力的直接影响和对大地水准面的间接影响概念。Heiskanen和Moritz将Stokes框架上的上述重力归算概念引入到Molodensky框架,称为“现代理论中的重力归算”,解释了在新框架下地形直接影响和间接影响的物理和几何意义。
将Helmert凝聚引入Molodensky框架后,直接地形影响(DTE)指地形Helmert凝聚引起的地面引力变化,相当于地面扰动重力的Helmert凝聚。第一间接地形影响(PITE)指地形Helmert凝聚引起的地面引力位(扰动位或高程异常)变化,第二间接影响(SITE)是第一间接影响“间接”产生的似地形表面正常重力变化。第一间接影响相当于地面高程异常(或地面扰动位)的Helmert凝聚,直接地形影响与第二间接影响之和相当于地面重力异常的Helmert凝聚。三者之间的关系符合重力测量基本方程:
式中,δgh为直接地形影响;ζh为第一间接影响;
 为第二间接影响。
为第二间接影响。
将“地球外空间”换成“地面”,“地形影响”换成“Helmert凝聚”,图 3的计算方案也适合直接地形影响和间接地形影响计算。 5.2 用Helmert凝聚表示高程异常高阶项
由地球外空间扰动位的唯一性可知,Stokes边值问题与Molodensky边值问题的解在地球外空间(含地面)是等价的。因此,重力异常的Helmert凝聚应该与Molodensky高阶项(一阶及以上各阶项之和)相近,由5.1节可知,高程异常Helmert凝聚等于重力异常Helmert凝聚的Stokes积分,因此,高程异常Helmert凝聚即第一间接影响PITE也应与高程异常高阶项相近。这样就可将地形Helmert凝聚理论引入Molodensky框架进行进一步研究。
图 4是利用5.1节方法按FFT快速算法得到的海岸带地区地面重力异常和地面高程异常的Helmert凝聚。比较图 1和图 4可以看出,地面重力异常Helmert凝聚与Molodensky一阶项G 1大致相等,高程异常第一间接影响与高程异常高阶项十分接近。

|
| 图 4 地面重力异常Helmert凝聚与高程异常第一间接影响 Fig. 4 Ground gravity anomaly Helmert condensation and first indirect effect on height anomaly |
同理,当地面边界条件为扰动重力、垂线偏差等其他类型重力场参数时,通过引入相应参数的Helmert凝聚代替该参数的高阶项,可直接得到以其他类型参数为边界条件的Molodensky框架中重力似大地水准面算法。如扰动重力Helmert凝聚的Hotine积分等于高程异常高阶项,利用式(7)积分公式由垂线偏差Helmert凝聚也可计算高程异常高阶项。
6 小结
本文针对海岸带多源重力数据和地形特点,通过理论分析和试算,对若干影响重力场和似大地水准面精化的若干关键问题进行了讨论,得出一些有益的结论:
(1) 我国海岸带Molodensky一阶项对高程异常的贡献在10~30 cm。为保证重力似大地水准面达到厘米级精度水平,必须在Molodensky框架中处理不同边界条件的边值问题。
(2) 重力场数据处理中大地测量基准不一致的影响会随数据处理算法的不同而变化,在多源重力数据处理过程中此类影响易变得不可预测和控制。
(3) 精细处理地形影响,是提升多源重力场数据处理水平的重要途径,地球外空间不同高度、任意类型重力场参数的地形影响、地形补偿和地形Helmert凝聚算法可以统一。
(4) 将地形Helmert凝聚理论引入Molodensky框架,可以解决以其他重力场参数(如扰动重力、垂线偏差等)为边界条件的似大地水准面精化问题。
| [1] | LI Fei. Determination of Geoid by GPS/Gravity Data[J]. Chinese Journal of Geophys.2005, 48(2):294-298.(李斐.应用GPS/重力数据确定(似)大地水准面[J].地球物理学报, 2005, 48(2):294-298.) |
| [2] | CHEN Junyong. Discussion on Geocentric 3D Coordinate System and Tidal Correction in China[J]. Geomatics and Information Science of Wuhan University, 2004, 29(11):941-949.(陈俊勇.关于我国采用三维地心坐标系和潮汐改正的讨论[J].武汉大学学报:信息技术版, 2004, 29(11):941-949.) |
| [3] | ZHANG Chuanyin, CHAO Dingbo, DING Jian, et al. Precision Topographical Effects for Any Kind of Field Quantities for Any Altitude[J]. Acta Geodaetica et Cartographic Sinica, 2009, 38(1):28-34.(章传银, 晁定波, 丁剑, 等.球近似下地球外空间任意类型场元的地形影响[J].测绘学报, 2009, 38(1):28-34.) |
| [4] | CHEN Junyong. Permanent Tides and Geodetic Datum[J]. Acta Geodaetica et Cartographic Sinica, 2000, 29(1):12-16.(陈俊勇, 永久性潮汐与大地测量基准[J].测绘学报, 2000, 29(1):12-16.) |
| [5] | LI Jiancheng, CHEN junyong, NING jinsheng, et al. Earth’s Gravity Field Approximation Theory and the Quasi-geoid 2000 Determination in China[M].Wuhan: Wuhan University Press, 2003.(李建成, 陈俊勇, 宁津生, 等.地球重力场逼近理论与中国2000似大地水准面的确定[M].武汉:武汉大学出版社, 2003.) |
| [6] | XU Houze. Some Problems on the Precise Determination of Regional Geoid in China[J]. Geospatial Information, 2006, 4(5):1-3.(许厚泽.我国精化大地水准面工作中若干问题的讨论[J].地理空间信息, 2006, 4(5):1-3.) |
| [7] | ZHANG Chuanyin, CHAO Dingbo, DING Jian, et al.Arithmetic and Characters Analysis of Terrain Effects for CM-order Precision Height Anomaly[J].Acta Geodaetica et Cartographic Sinica, 2006, 35(4):308-314.(章传银, 晁定波, 丁剑, 等.厘米级高程异常地形影响的算法及特征分析[J].测绘学报, 2006, 35(4):308-314.) |
| [8] | SJÖBERG L E. Topographical Effects by the Stokes-Helmert Method of Geoid and Quasi-geoid Determination[J]. Journal of Geodesy, 2000, 74(2): 255-268. |
| [9] | FEATHERSTONE W E, KIRBY J F.The Reduction of Aliasing in Gravity Anomalies and Geoid Heights Using Digital Terrain Data[J]. Geophysical Journal International, 2000, 141: 204-212. |
| [10] | SANS F, RUMMEL R. Geodetic Boundary Value Problems in View of the One Centimeter Geoid[M]. Berlin: Springer-Verlag, 1997. |
| [11] | MARTINEC Z, VANÍČEK P. Direct Topographical Effect of Helmert’s Condensation for a Spherical Approximation of the Geoid[J]. Manuscr Geod. 1994, 19: 257-268. |
| [12] | VANÍČEK, HUANG J, NOVÁK P, et al. Determination of the Boundary Values for the Stokes- Helmert Problem[J]. Journal of Geodesy, 1999, 73: 180-192. |