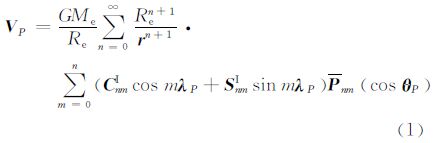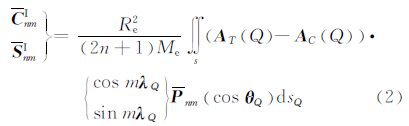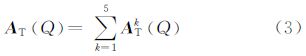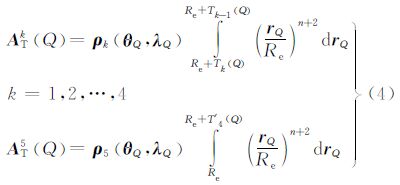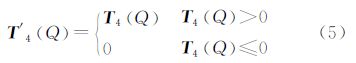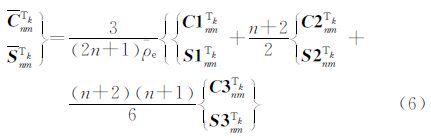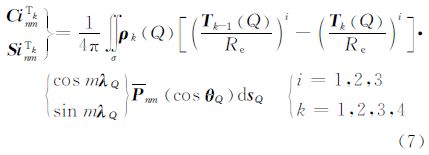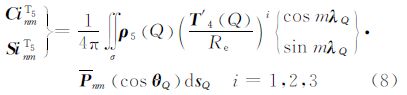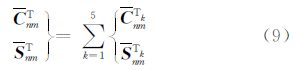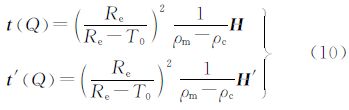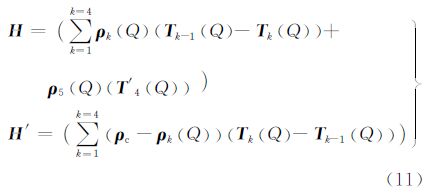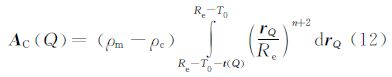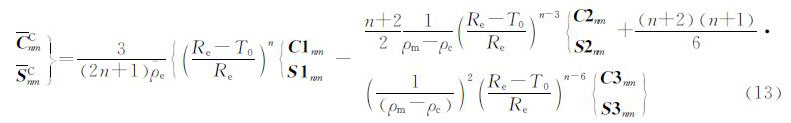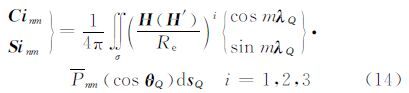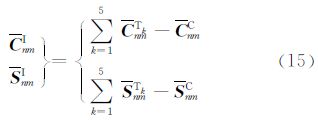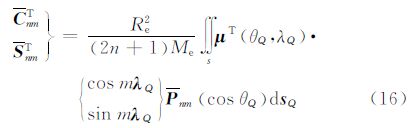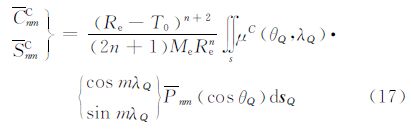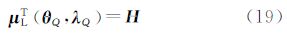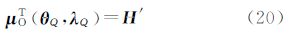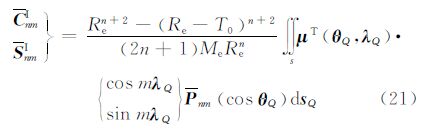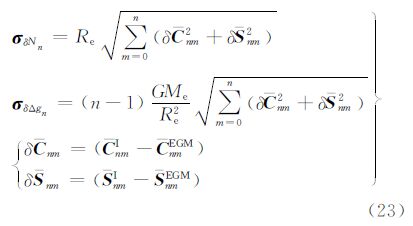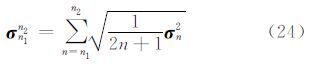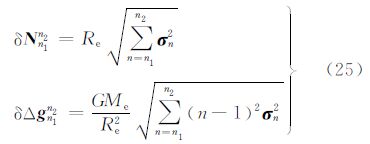2. 西安测绘研究所,陕西 西安 710054; 3. 61287部队,四川 成都 610036;
3. 61287部队,四川 成都 610036;
4. 武汉大学 地球空间环境与大地测量教育部重点实验室,湖北 武汉 430079;
5. 63801部队,四川 西昌 615042
2. Xi’an Research Institute of Surveying and Mapping, Xi’an 710054, China;
3. 61287 Troops, Chengdu 610036, China;
4. Key Laboratory of Geo-space Environment and Geodesy of Ministry of Education, Wuhan University, Wuhan 430079, China;
5. 63801 Troops, Xichang 615042, China
1 引 言
地壳均衡理论是基于流体静力平衡原理提出的一种对地壳构造进行解释的理论,意指地壳的各个地块在一定深度处于等压力的状态[1, 2]。该理论自提出以来受到了大地测量学家和地球物理学家的关注[3],并在均衡补偿模式[4]、重力空白区填补[5]、地壳厚度和密度推估[6, 7, 8]、地壳垂直运动[9]、月球均衡状态及月壳厚度[10]等方面进行了较为广泛的研究,地壳均衡学说业已被越来越多的地球物理资料(如重力资料、地震资料等)所证实[11]。但是地球内部质量的实际分布一直制约着该理论的进一步发展,随着科技的发展以及人类对地球内部构造认识的逐步深入,越来越多的学者加入到该理论的研究当中[12, 13, 14]。
为了研究地球内部密度分布在均衡理论应用中的贡献,国内外的学者开展了大量的研究工作[15]。文献[8]通过试验验证了地壳信息在均衡理论应用中的贡献具有可逆性;文献[16]对CRUST 2.0模型的各层地壳数据进行了调和分析,得到了完全至90阶次的级数展开模型,分析了模型中的Moho面以及不同层地壳信息对构建重力位模型的贡献;文献[13, 17]基于CRUST 2.0和EGM2008模型计算了不同地壳层对重力异常的贡献量级,得到了1°分辨率的重力场扰动场元的改正量;文献[18]研究了CRUST 2.0模型在区域重力异常计算中的贡献,验证了该模型在研究区域内应用的可行性;文献[19]研究了地壳构造在区域均衡理论中的应用,分析了不同山区的均衡状态,给出了地壳的稳定状态对区域均衡异常的影响,进而分析了区域均衡效应与地震的关系;文献[6]基于CRUST 2.0和EGM2008模型研究了Moho面处地幔与地壳的密度差,并给出了Moho厚度及密度差的估值范围。
地形均衡重力场模型是地壳均衡理论应用研究的一个重要方向,反映了地幔结构与地形质量分布的关系,由其计算的大地水准面高等物理量能够为重力场模型与地球内部构造之间的关系研究提供一定的参考。地壳均衡理论的应用在现有的地球重力场模型构制中也有体现,EGM2008的构制中采用了地形数据、卫星和地面重力数据等。
随着数据精度和分辨率的不断提高,高分辨率的均衡理论应用逐渐成为学者们研究的热点,地形、地壳数据在重力场模型构建中对不同频段的贡献也吸引着大地测量学者的目光,基于此,本文尝试在SRTM 地形数据和CRUST 2.0全球地壳模型的支撑下,研究不同补偿机制下地壳数据在构建地球重力场均衡位模型中的贡献,并分析补偿深度对均衡位模型的影响,以为该地壳模型在实测数据处理中的应用做理论铺垫。
2 顾及地球物理信息的均衡位模型定义仅考虑地形数据并进行了地壳密度假设的均衡模型为理想均衡模型,其提出的背景和参数定义主要参考了文献[1, 20]。大量地球物理以及大地测量资料说明:在全球范围内,大约有90%的区域达到地壳均衡补偿状态,但并不是某一种单一的补偿模型能够与之完全符合[1]。本文以SRTM全球地形数据为基础,以Airy均衡模型和面凝聚模型作为补偿机制[15, 21],讨论地壳数据在均衡位模型构建应用中的有效性和适用性。
2.1 可见地形分层的模型理想均衡理论将地表分为陆地和海洋两大部分,并假设陆地、海洋部分的密度为常数,可以构建基于SRTM地形数据的均衡位模型。若顾及地球表面可见地形的实际情况,分层考虑地壳各层的密度和厚度,基于CRUST 2.0模型数据,依据均衡原理可以计算得到基于可见地形的均衡位模型。
分析CRUST 2.0模型,可见地形部分包括了该模型中的前5层数据,即水层、冰层、软沉积层、硬沉积层和上地壳在海平面以上的部分,故理想均衡模型中的地形部分即用5层模型代替,且假定模型中Moho面上下的密度差为地幔密度ρm和地壳平均密度ρc之差。令模型中读取的水层、冰层、软沉积层、硬沉积层和上地壳5层模型的深度分别为Tk(Q)(注:以海平面为起算点,凸起部分为正,凹陷部分为负),且5层模型的密度分别为ρk(Q)。
均衡意义上的球外任一点P引力位级数表达式为[15]
式中
式中,地形部分影响为
式中
式中,rQ为流动点Q的向径;Re为地球平均半径;Me=4/3πρeRe3为球近似下的地球总质量;ρe表示地球平均密度。
对式(4)积分并代入上下限,展开至三阶项,代入式(2)可得
式中
将水准面之上和硬沉积层之下部分地形质量的引力进行积分并展开至三阶项,代入式(2)可得该层对应的模型系数,其与前4层的区别在于面积分的被积函数不同,即
故可得可见地形部分的引力位系数
考虑可见地形部分的详细分层,其各层对于补偿处均有相应的响应,实际计算中对该部分的补偿影响做如下简化,令水准面之下和Moho面之上部分的正常地壳部分的密度为常值ρc,而地幔密度为常值ρm。依据Airy-Heiskanen均衡模型补偿原理,补偿面处的山根t(Q)和反山根t′(Q)的线性估值公式为
式中
因此,补偿质量部分的径向积分为
式中,T0为补偿深度。
分析补偿部分质量,将上式积分后依据二项式定理展开到三阶项,代入式(2),得补偿质量部分的模型位系数
式中
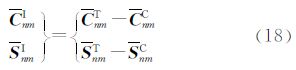
将前面分别计算得到的地形和补偿质量部分的模型位系数组合,可得可见地形分层情况下均衡位模型系数
2.2 顾及地球物理信息的面凝聚模型在理想的面凝聚模型中,补偿质量是根据均衡“双极”原理进行密度模型假设的,其与实际地壳密度的分布有一定的出入。鉴于国际上公开发布的CRUST 2.0地壳模型的可用性,下面考虑将其模型数据融入均衡面凝聚模型的构建中。
可见地形部分质量对外部点的引力位系数模型为
式中,μT(θQ,λQ)表示地形面密度。
补偿部分质量对外部点的引力位系数模型为
式中,μC(θQ,λQ)表示补偿质量的面密度,且有μC(θQ,λQ)=-μTθQ,λQ。
综合上述两式,得
可以发现,只要构建出一定分辨率的面密度模型,即可计算出相应阶次的模型位系数。参考上文构建Airy模型中的可见地形质量部分内容,可见地形的面密度构建应该考虑水层、冰层、软沉积层、硬沉积层以及上地壳在大地水准面之上的部分质量。因此,陆地部分的地形面密度为
而海洋部分的地形面密度为
综合两部分贡献,即可得均衡位系数模型
3 模型评估试验中,地球平均密度和平均半径分别取ρe=5500 kg/m3、Re=6371 km,地壳平均密度取ρc=2670 kg/m3,地幔平均密度取ρm=3270 kg/m3,海水平均密度取ρw=1025 kg/m3,对地壳的厚度和密度值进行相应的前期处理[22],依据式(11)构造相应的面积分被积函数,应用轮胎调和分析技术[23],得到完全至2160阶次的位系数模型。轮胎调和分析是一种自洽的调和分析,能够克服平滑因子不精确等原因引起的误差,实现快速、高效并且稳定的重力场反演。仅采用5′分辨率的SRTM格网地形数据,得到理想状况下的均衡位模型,以EGM2008[24]为参考模型,利用模型阶方差、大地水准面阶误差、重力异常阶误差以及频段间的累积误差等来分析CRUST 2.0在构建均衡位模型中的贡献。以面凝聚模型为例,分析补偿深度T0在模型构建中的影响。
CRUST 2.0模型的数据分辨率为2°×2°,采用最小曲率曲面拟合法[25]将各层地壳密度和厚度数据加密为5′,以满足数据分辨率与模型阶次的对应关系。文中模型阶方差σn2计算公式为[21]
大地水准面阶误差σδNn和重力异常阶误差σδΔgn的计算公式为[26, 27]
式中,(CnmEGM,SnmEGM)为参考地球重力场模型EGM2008的扰动位系数;δΔg和δN分别表示重力异常差和大地水准面高之差。
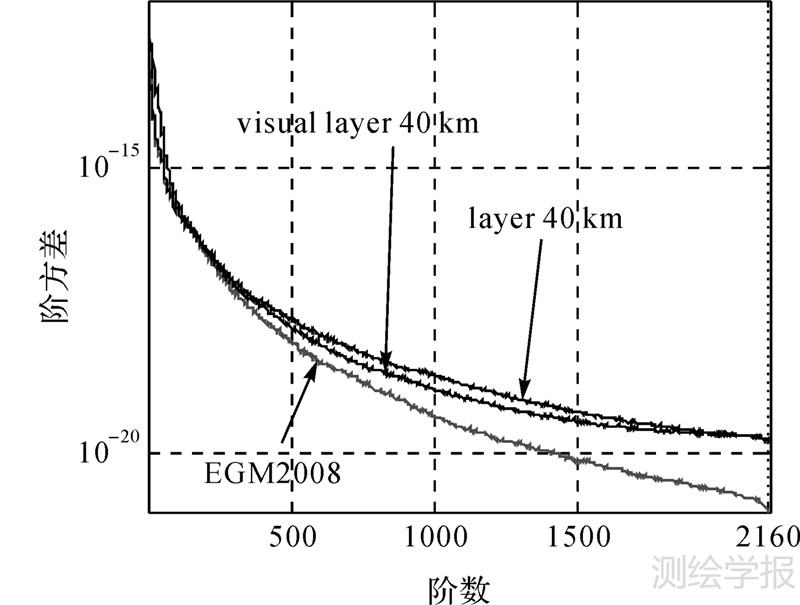
3.1 面凝聚模型分析补偿深度对顾及地壳模型的面凝聚均衡位模型的影响以及补偿深度相同时地壳模型在位模型构建中的影响。经过试验分析,理想面凝聚模型的补偿深度为40 km(称其为原模型)时,其阶方差曲线与参考模型一致性较好。下文重点分析该补偿深度下,顾及地壳信息的面凝聚模型的应用效果,具体结果如图 1~图 3所示,图中layer和visual layer分别指代顾及地壳信息前后的均衡位模型。
|
| 图 1 3种位系数模型的阶方差曲线 Fig. 1 Comparison of degree variance of the three potential coefficient models |

|
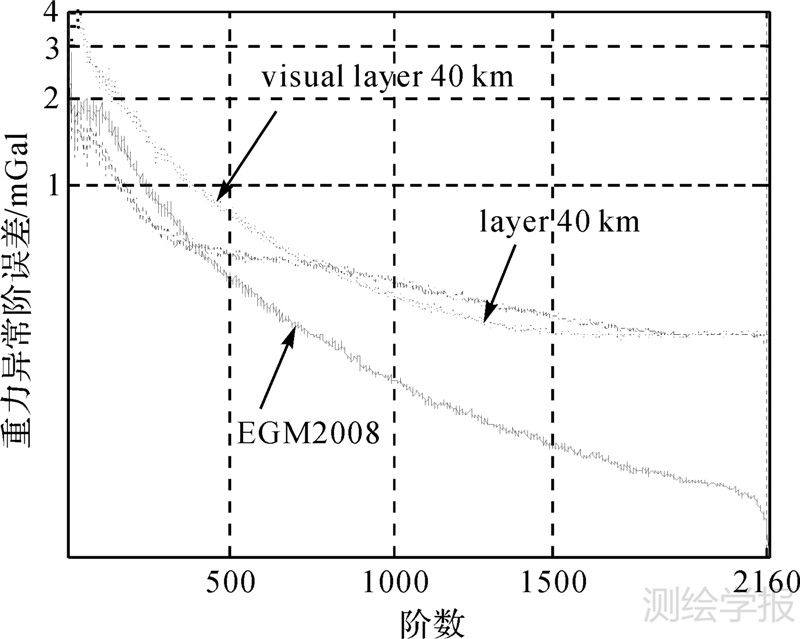
| 图 2 3种位系数模型的大地水准面阶误差 Fig. 2 Comparison of geoid degree error of the three potential coefficient models |
|
| 图 3 3种位系数模型的重力异常阶误差 Fig. 3 Comparison of gravity anomaly degree error of the three potential coefficient models |
对图 1~图 3进行对比分析,可以得到如下结论:
(1) 面凝聚模型机制下,考虑可见地形模型后,模型在超高阶部分(如400~1800阶)的阶方差要比原模型更加接近EGM2008模型,由此可见地形模型中的分层密度和厚度信息能够改善位模型的高频部分。
(2) 对比500阶次以内的两种模型与EGM2008模型的阶方差曲线,可以看出加入地壳模型后的位模型在低阶部分的补偿强度要弱于加入地壳模型之前的位模型,而在中高阶部分,顾及地壳模型的位模型补偿效果要更明显,这是因为地壳模型中包含了较为丰富的重力场高频信息。
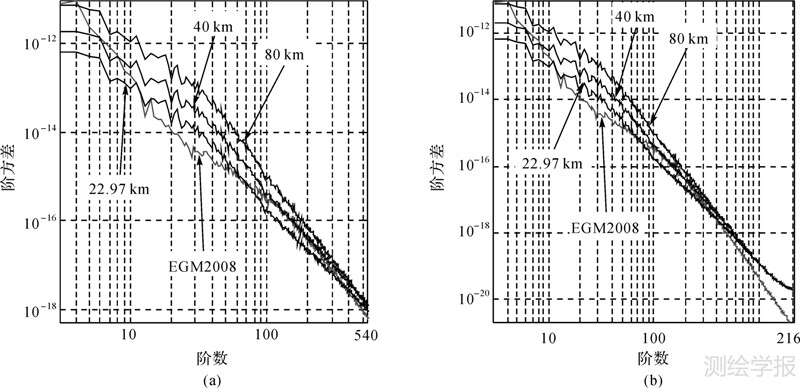
补偿深度一直是均衡模型应用中的重要参数,图 4给出补偿深度对顾及地壳信息的面凝聚模型影响的阶方差曲线,研究中,选取的补偿深度为10 km整数。
|
| 图 4 不同补偿深度的面凝聚模型与EGM2008的阶方差曲线 Fig. 4 Comparison of degree variance of the two potential coefficient models with different compensation depth |
分析图 4可以看出,补偿深度直接影响补偿效果。补偿深度为40 km时,模型在中高阶部分与参考模型的一致性较好;在模型的低阶部分,补偿深度越小,补偿的效果越明显;而在模型的超高阶部分,补偿几乎没有起到任何作用,这与没有考虑地壳模型时的结论是一致的,说明补偿部分对2000阶以上模型的贡献为零。实用中,可以考虑应用某种法则对不同频段应用不同的补偿深度以达到与参考模型一致性最好的均衡位模型。
需要说明的是,补偿深度中的22.97 km是Moho面深度的算术平均值,为了研究其作为均衡补偿面时的补偿效果,将其计算结果与其他的补偿深度相比,结果显示,在反映均衡效应较为明显的模型中高阶部分,其补偿效果不是最佳的,故22.97 km不是最佳补偿深度。
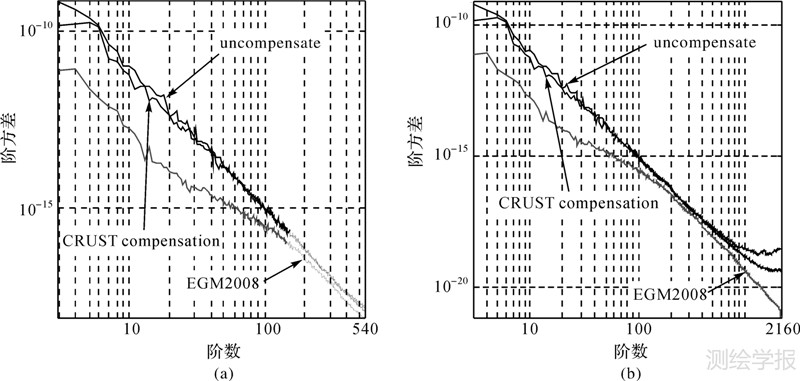
3.2 Airy模型考虑地壳模型中的第7层Moho面作为地幔与地壳的分界面,并计算均衡位模型,将其与EGM2008参考模型阶方差作比较,结果如图 5所示(补偿深度为50 km)。
|
| 图 5 顾及CRUST 2.0中Moho面的Airy模型与EGM2008的阶方差曲线 Fig. 5 Comparison of degree variance of EGM2008 and Airy potential coefficient model considering CRUST 2.0 model |
从图 5对比分析可以看出:
(1) 地壳模型中的Moho面在Airy模型中应用时能够在低阶部分有一定的补偿作用,但是效果不是很明显,尤其是在50阶之后,而中高阶部分,几乎没有任何补偿效果。
(2) 从图 5(b)的超高阶部分可以看出,地壳模型在该部分的阶方差曲线在未补偿的曲线上方,这说明此时的地壳模型数据反而影响了原地形位模型的精度,这主要与地壳数据分辨率、精度等因素有关。
(3) 补偿深度不同时,补偿效果几乎相同,这与地壳模型中Moho面的确定机制有关,其与重力场反映的地壳和地幔的分界面不完全一致。
为了进一步研究补偿机制间的关系,引入统计量阶次n1和n2间的模型阶误差、大地水准面高和重力异常的均方根,三者计算式为
和
对EGM2008、layer 40 km、visual layer 40 km和Airy 40 km 4个模型进行统计计算,对比分析补偿机制和CRUST 2.0在构建模型中的贡献。具体计算思路为分别计算4个模型阶次为2~51、51~120、121~360、361~1080和1081~2160等5个区间的统计量,以EGM2008计算量为参考,分别计算其他3个模型的统计量与相应参考值的相对误差,计算结果如表 1~表 3所示。
| 2~51 | 51~120 | 121~360 | 361~1080 | 1081~2160 | |
| EGM2008 | 4.462 1×E-06 | 1.278 8×E-07 | 6.634 0×E-08 | 1.329 2×E-08 | 1.677 2×E-09 |
| layer 40/(%) | 60.12 | 5.89 | 5.10 | 61.03 | 167.85 |
| visual layer 40/(%) | 13.84 | 48.09 | 6.84 | 36.35 | 127.53 |
| Airy 40/(%) | 76.79 | 22.08 | 13.01 | 33.02 | 187.94 |
| 2~51 | 51~120 | 121~360 | 361~1080 | 1081~2160 | |
| EGM2008/cm | 30.34 | 1.26 | 0.62 | 0.13 | 0.02 |
| layer 40/(%) | 67.46 | 5.45 | 2.10 | 53.28 | 160.10 |
| visual layer 40/(%) | 31.67 | 55.08 | 5.59 | 32.52 | 117.75 |
| Airy 40/(%) | 81.99 | 21.57 | 15.74 | 26.77 | 173.15 |
| 2~51 | 51~120 | 121~360 | 361~1080 | 1081~2160 | |
| EGM2008/mGal | 17.06 | 14.71 | 16.98 | 10.04 | 4.12 |
| layer 40/(%) | 21.42 | 6.92 | 7.77 | 65.58 | 171.46 |
| visual layer 40/(%) | 85.10 | 40.82 | 7.84 | 38.12 | 135.38 |
| Airy 40/(%) | 39.02 | 23.12 | 10.50 | 36.70 | 209.26 |
| 注:1 mGa=10-5/s2 | |||||
分析表 1~表 3,可以得到如下结论:
(1)与前文定性分析一致,加入地壳模型后,模型在超高阶部分较原模型有较大程度的提高,而在中低阶部分,原模型要更加接近参考EGM2008模型,且模型的中阶部分要比低阶和高阶部分更接近参考模型。
(2) 重力异常的频谱分布较大地水准面高更广,加入地壳模型后的重力异常精度要比原模型在361~1080频段提高2.76 mGal(1 mGal=10-5 m/s2),而在1081~2160频段部分,其仅有一定的改善效果。
(3) 补偿深度都为40 km时,面凝聚模型在360阶内的重力异常精度要比Airy模型高8.49 mGal,但是在360~1080频段内,Airy模型要比面凝聚模型高2.90 mGal,这是由补偿机制的不同决定的。
4 结论和展望本文主要研究了CRUST 2.0全球地壳数据在面凝聚模型和Airy均衡位模型构建中的应用,简要分析了CRUST 2.0地壳数据的分层结构,推导了可见地形分层模型在两种补偿机制中应用的实用计算公式,利用SRTM地形数据构建了不同补偿机制下完全至2160阶次的理想均衡位模型,对比分析了地壳数据和补偿深度对不同补偿机制的影响。试验分析表明,面凝聚模型中,以重力异常为统计量,全球地壳模型能在361~1080频段内较理想模型提高2.76 mGal;地壳数据中Moho面厚度的平均值22.97 km不是面凝聚模型的最佳补偿深度,补偿深度为40 km为此时最佳补偿深度,其阶方差曲线与参考模型的一致性更好,补偿深度的对模型超高阶部分影响较小;加入地壳数据后的均衡位模型在361~1080频段内较原模型有较大改善;相同补偿深度的两种补偿机制在位模型不同频段的优劣性是不一致的。
此次研究缺乏实测区域的重力数据的检验,若能够将更高精度和分辨率的地壳模型以及地形数据应用于均衡位模型的构制中,并经实测应用区域的系统校正,以此推估空白区的重力数据,结合卫星重力、卫星测高等实测数据,可构建高精度、高分辨率的地球重力场模型和大地水准面模型,这一应用将是笔者以后的研究方向。
| [1] | HOFMANN-WELLENHOF B,MORITZ H. Physical Geodesy[M]. NewYork: Springer, 2005. |
| [2] | LU Zhonglian. Theory and Methods of theEarth's Gravity Field[M]. Beijing: PLA Publishing House, 1996. (陆仲连. 地球重力场理论与方法[M]. 北京: 解放军出版社, 1996.) |
| [3] | GUO Chunxi,WANG Huimin,WANG Bin. Determination of High Resolution Grid Terrain and Isostatic Corrections in All China Area[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(3): 201-205. (郭春喜,王惠民,王斌. 全国高分辨率格网地形和均衡改正的确定[J]. 测绘学报, 2002, 31(3): 201-205.) |
| [4] | LIU Zuanwu,LU Zhonglian. Discussion on the Isostatic Earth Model [J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(4): 308-312. (刘缵武,陆仲连. 关于地壳均衡模型的讨论[J]. 测绘学报, 1999, 28(4): 308-312.) |
| [5] | MAKHLOOF A A,ILK K. Effects of Topographic:Isostatic Masses on Gravitational Functional at theEarth's Surface and at Air Borne and Satellite Altitudes[J]. Journal of Geodesy, 2007, 82(2): 93-111. |
| [6] | SJÖBERG L E,BAGHERBANDI M. A Method of Estimating the Moho Density Contrast with a Tentative Application of EGM08 and CRUST 2.0[J]. Acta Geophysica, 2011, 59(3): 502-525. |
| [7] | SJÖBERG L E. Solving Vening Meinesz-Moritz Inverse Problem in Isostasy[J]. Geophysical Journal International, 2009, 179: 1527-1536. |
| [8] | ABD-ELMOTAAL H A. Isostatic Response of the Earth's Crust Derived by Inverse Isostasy[J]. Journal of Geodynamics, 2004, 37(7): 139-153. |
| [9] | ZHANG Qin,FAN Yizhong. The Isostatic Theory and the Mathematical Model of Crust Vertical Movement[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(3): 233-237. (张勤,范一中. 地壳垂直运动的均衡理论及其分析模型[J]. 测绘学报, 2001, 30(3): 233-237.) |
| [10] | FENG Hai,LI Jiancheng,LI Dawei,et al. Airy Isostasy on the Moon: Implications for Crustal Thickness[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 543-548. (丰海,李建成,李大炜,等. 月球Airy均衡状态与月壳厚度估计[J]. 测绘学报, 2012, 41(4): 543-548.) |
| [11] | GÖTTL F,RUMMEL R. A Geodetic View on Isostatic Models[J]. Pure and Applied Geophysics, 2009, 166: 1247-1260. |
| [12] | CHEN Shi,WANG Qianshen,ZHU Yiqing,et al. Temporal and Spatial Features of Isostasy Anomaly Using Gravitational Admittance Model at Eastern Margin of Tibetan Plateau[J]. Chinese Journal of Geophys, 2011, 54(1): 22-34. (陈石,王谦身,祝意青,等. 青藏高原东缘重力导纳模型均衡异常时空特征[J]. 地球物理学报, 2011, 54(1): 22-34.) |
| [13] | TENZER R,HAMAYUN K,VAJDA P. Global Maps of the CRUST 2.0 Crustal Components Stripped Gravity Disturbances[J]. Journal of Geophysical Research: Solid Earth, 2009, 114(B5): 105-114. |
| [14] | RAPP R H. The Ohio State 1991 Geopotential and Sea Surface Topography Harmonic Coefficient Models[R]. Columbus: Ohio State University, 1991. |
| [15] | RUMMEL R,RAPP R,SUNKEL H,et al. Comparisons of Global Topographic Isostatic Models to theEarth's Observed Gravity Field[R]. Columbus: Ohio State University, 1988. |
| [16] | TSOULIS D. Spherical Harmonic Analysis of the CRUST 2.0 Global Crustal Model[J]. Journal of Geodesy, 2004(78): 7-11. |
| [17] | PAVLIS N K,HOLMES S A,KENYON S C, et al. An Earth Gravitational Model to Degree 2160: EGM 2008[R]. Vienna: General Assembly of the European Geosciences Union, 2008. |
| [18] | HU Minzhang,LI Jiancheng. Computation of Airy-Heiskanen Isostatic Gravity Anomaly with Considering CRUST Density Model[J]. Journal of Geodesy and Geodynamics,2010, 30(5): 48-52. (胡敏章,李建成. 顾及地壳密度模型的Airy-Heiskanen均衡重力异常的计算[J]. 大地测量与地球动力学, 2010, 30(5): 48-52.) |
| [19] | WANG Qianshen,TENG Jiwen,ZHANG Yongqian,et al. The Crustal Structure and Gravity Isostasy in the Middle Western Sichuan Area[J]. Chinese Journal of Geophysical, 2009, 52(2): 579-583. (王谦身,滕吉文,张永谦,等. 四川中西部地区地壳结构与重力均衡[J]. 地球物理学报, 2009, 52(2): 579-583.) |
| [20] | MORITZ H. The Figure of the Earth: Theoretical Geodesy and theEarth's Interior[M]. CHEN Junyong, ZUO Chuanhui, Trans. Beijing: Surveying and Mapping Press, 1992:207. (莫里茨 H. 地球形状:理论大地测量学和地球内部物理学[M]. 陈俊勇,左传惠,译. 北京: 测绘出版社, 1992: 207.) |
| [21] | TSOULIS D. A Comparison between the Airy-Heiskanen and the Pratt-Hayford Isostatic Models for the Computation of Potential Harmonic Coefcients[J]. Journal of Geodesy, 2001, 74(9): 637-643. |
| [22] | COLOMBO O L. Numerical Methods for Harmonic Analysis on the Sphere[R]. Columbus: Ohio State University, 1981. |
| [23] | ZHANG Chuanding,XU Houze,WU Xing. Torus Problem of the Harmonic Analysis in theEarth's Gravity Field[C]//Proceedings of Geodesy and Geodynamics Development. Wuhan: Science and Technology Press, 2004. (张传定,许厚泽,吴星. 地球重力场调和分析中的“轮胎”问题[C]//大地测量与地球动力学进展. 武汉: 科学技术出版社, 2004.) |
| [24] | ZHANG Chuanyin,GUO Chunxi,CHEN Junyong,et al. EGM 2008 and Its Application Analysis in Chinese Mainland[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 283-289. (章传银,郭春喜,陈俊勇,等. EGM 2008地球重力场模型在中国大陆适用性分析[J]. 测绘学报, 2009, 38(4): 283-289.) |
| [25] | SMITH W H F,WESSEL P. Gridding with Continuous Curvature Splines in Tension[J]. Geophysics, 1990, 55: 293-305. |
| [26] | WU Xing. Theory and Methods of Satellite Gradiometry Data Processing[D]. Zhengzhou:Information Engineering University, 2009. (吴星. 卫星重力梯度数据处理理论与方法[D]. 郑州: 信息工程大学, 2009.) |
| [27] | LIU Xiaogang. Theory and Methods of theEarth's Gravity Field Recovery from GOCE Data[D]. Zhengzhou: Information Engineering University, 2011. (刘晓刚. GOCE卫星测量恢复地球重力场模型的理论与方法[D]. 郑州: 信息工程大学, 2011.) |