地图是空间信息的载体,而图形要素是地图传递空间信息的主要形式。地图设计与制作的目的在于传递空间信息,通过对空间信息的获取、感知、加工、分析和综合,可以揭示区域空间分布、变化的规律。文献[1]指出:“信息是用来消除随机不确定性的东西”。文献[2]把信息的概念引入地图制图学,此后地图的信息传输功能受到制图学界广泛关注,开创了现代地图学的新领域——地图信息传输理论,并将地图信息传输理论与制图综合理论、地图感知论、地图模型论、地图符号学并列为现代地图学理论的基本内容[3]。
鉴于地图传输空间信息的属性,地图设计、制图综合的一个重要问题是地图载负的信息量容量(即信息量度量问题),同时该问题也是地图质量评价的一个重要方面。为了合理地计算地图信息量,则需要科学地界定地图信息的来源、内容构成以及地图信息量的度量方法,这亦是地图信息论需要解决的主要问题。鉴于此,本文以点状地图为例,基于点状地图信息本质,从点要素分布特征的视角分析点状地图空间信息内容的构成,并结合人的认知特点确定地图信息量度量模型,最终建立点状地图空间信息量的度量方法。
2 现有的地图信息量度量方法、存在的主要问题及本文的研究策略 2.1 现有的地图信息量度量方法文献[4]将信息论引入制图领域,提出地图的符号信息熵概念和计算模型。文献[5]从地图实体多样性和差异性角度提出度量地图信息的拓扑信息熵。文献[6]分析认为地图信息源由多样性的地图实体及其差异性的特征集合描述,提出了基于Voronoi邻接阶数的拓扑信息熵、基于Voronoi邻接距离差异的度量信息熵和基于点数的位置信息熵的度量方法,并将信息量度量用于评价制图质量。文献[7] 将地图信息内容分为几何信息、拓扑信息和专题信息,借助Voronoi空间划分,采用Shannon信息熵模型建立了点状地图基于Voronoi区域面积的几何信息度量、基于Voronoi邻接度的拓扑信息度量和专题信息度量方法。文献[8]提出了基于统计数量的点要素信息度量方法,并对这几种度量方法进行了评价研究,并探讨了基于Voronoi区域的点要素信息量的规范化问题。文献[9]发展了一种地图信息量计算的栅格方法,并建立了地图数据量与信息量之间的非线性关系。随后文献[10]验证了该方法得到的信息量与人所认知的信息量有一定的线性关系。最近,文献[11]从元素层次、邻域层次和整体层次对地图上等高线信息进行描述,结合等高线表达地形的差异性和多样性特征建立了相应的信息度量方法。
总的说来,现有工作主要是从不同角度分析地图信息类型和内容构成,并采用Shannon信息熵理论,分别针对地图的几何信息、拓扑信息、专题信息提出了相应的度量方法。
2.2 存在的主要问题分析纵观现有的地图信息量度量方法,大都套用建立在通信领域信息论基础上的Shannon信息熵模型,并以某个特征上个体与总体的比值代替Shannon熵模型中的概率。这种机械套用的方式用于地图空间信息量度量时,存在的最大问题是忽略了地图空间信息主要产生于点要素空间分布的多样性和差异性。如图 1所示,相同图幅范围的两幅地图具有相同点要素数目,其中图 1 (a)点要素分布均匀,点要素间相对空间位置关系差异性较小,而图 1 (b)不均匀,点要素间相对空间位置关系差异性较大,因而图 1 (a)点要素空间分布比图 1 (b)更复杂多样化,相应的,图 1 (a)包含的点要素分布空间信息量较小。而根据现有度量方法(如文献[7]的方法),“均匀平衡状态”下信息量最大,即图 1 (a)空间分布特征产生的几何信息量比图 1 (b)大。表明,简单的以个体与总体的比值作为概率;不考虑个体之间特征差异性的方法,将导致度量结果有悖于空间认知和信息产生的本质(特征的多样性和差异性)。

|
| 图 1 不同空间分布的点状地图 Fig. 1 Two point-shaped maps with different spatial distributions |
此外,在地图信息内容的划分方面,现有研究普遍将点状地图的信息内容分为几何信息、拓扑信息、专题信息。这种划分方式考虑了要素个体分布特征,却忽略了地图上大量潜在的由要素组合形成的聚群结构特征。事实上,聚群结构是地图表达和空间分析的一类重要集合对象[12, 13, 14],通过聚群结构分析可以提取客观世界中存在的空间相关规律,辅助决策支持。同时,点的聚群分布空间结构信息通常是进行点要素合并或典型化等操作的依据[15]。由此可见,聚群结构信息是点状地图信息内容的重要组成部分。
2.3 本文研究策略
地图信息产生的根源是地图上要素及其分布的多样性与差异性。因此,在地图信息量计算模型的选取与确定中,既要满足信息量的非负性、可加性、反转对称性,同时又要能够恰当地描述要素及其分布特征的多样性和差异性。据文献[16],本文选择基于特征的信息量计算模型作为地图信息量度量模型,表达为
式中,wi为特征w上第i个标准化的定量描述指标值;Iw为特征w的多样性或差异性产生的信息量。如图 2所示,3组点状地图中图(a)与(d)之间的差异主要体现在点要素几何分布方面,与点要素间的分布密度直接相关,称这类空间差异产生的信息为几何分布信息;图(b)与(e)之间的空间差异主要体现在点要素拓扑邻接关系方面,与点要素的拓扑邻接关系相关,称这类差异产生的信息为拓扑邻接信息;图(c)与(f)之间的差异主要体现在点要素的聚群结构分布方面,包括点群结构的数量、点群结构中点要素数量及其分布特征存在的差异,称这类空间差异产生的信息为聚群结构信息。
结合点状地图的空间特征及信息内容构成,本文分别从点要素分布的几何分布特征、拓扑邻接特征和聚群结构特征出发,分别提取这些特征的定量描述指标,并采用基于特征的信息量模型来度量点状地图的几何分布信息量、拓扑邻接信息量和聚群结构信息量,具体研究策略如图 3所示。

|
| 图 2 点状地图包含的空间信息内容 Fig. 2 Potential spatial information content contained in point-shaped maps |

|
| 图 3 点状地图信息量度量的策略 Fig. 3 A strategy for measuring the information content of a point-shaped map |
文献[4]从制图学角度首次将信息概念引入地图学并提出符号类型信息熵,明确了地图信息产生于地图要素的多样性。文献[5]指出地图信息产生于空间差异性。从地图信息的内涵可知,能够从地图上获得丰富的信息,是由于感知到地图要素及其分布特征的多样性和差异性。点要素不具备形状和大小特征,若不考虑专题属性,点状地图的信息主要产生于点要素空间分布的多样性与差异性,这主要表现在几何分布密度、拓扑邻接和聚群结构等方面。下面分别从几何分布特征、拓扑邻接特征和聚群结构特征等方面来描述点状地图的空间分布特征。
在点状地图的几何分布特征方面,点要素分布密度的差异性反映分布的均匀性程度。点要素的分布密度与相邻点要素间的距离和方向关系共同决定,数值上与对应Voronoi区域面积成反比。Voronoi区域面积越大,要素分布越稀疏,总体上要素数量越少,对应信息量也越少。Voronoi区域面积差异越大,点位分布越不均匀,分布形式越丰富,因而信息量越大。由此可见,由点要素几何分布特征产生的几何信息量与点要素Voronoi区域面积及其差异性的大小分别成负相关和正相关的关系。在点状地图的拓扑邻接特征方面,Voronoi图对应的拓扑相邻是主要的邻接关系,一般用拓扑邻接度表示。拓扑邻接度反映要素之间的连通性,邻接度的差异反映空间连通关系的差异,差异越大则拓扑信息量越大。在点要素分布的局部结构特征方面,聚群结构是空间分布分析的重要对象。目前国内外学者对于聚群的描述进行了大量研究,概括点群描述参数包含点数、Voronoi面积及邻接度、点间距离、分布范围、分布密度、分布形状和分布轴线[12, 13, 14, 15]。从空间认知角度,点群中的点数反映点群规模;几何分布范围反映点群的聚集性程度;分布密度与点数及分布范围相关,但同时也反映松散耦合性,具有独立特征性质。如图 4,点群①与②的分布范围、①与③的点数分别接近,但由于分布密度存在差异而使点群结构不同,①的分布密度大,显然其耦合性程度高。②与③中的点数、分布范围虽有较大差异,但其分布密度非常接近,群内松散耦合性程度基本相等。而③与④的点数和密度接近,但③呈圆盘状分布而④呈带状分布,致使③的分布面积比④的大,从而点群存在差异,视觉上点群③与④具有不同的结构。据此,本文选择点要素数量、分布密度、分布面积指标描述聚群结构特征。

|
| 图 4 点群结构特征 Fig. 4 The characteristics of point clusters |
如前所述,几何分布信息由点要素分布密度及其差异性产生,信息量的大小与总体密度大小和局部密度间的差异大小成正相关关系。局部密度分布可由Voronoi图间接表达,大小与各点要素的Voronoi区域面积成反比。Voronoi区域面积在物理意义上表达的是点要素的辐射范围,这不仅与周围点要素分布相关,同时也受点要素自身辐射能力的限制。如图 5所示,地图表达的点要素及其分布完全相同,图幅范围不同,所对应的Voronoi图不尽相同,这主要产生于边界处。因此,本文通过设置阈值对边界进行收缩处理构建Voronoi图,其中阈值可取Delaunay三角网内部边长的平均值。该改进方法构建的Voronoi图只与要素及其空间位置分布相关。

|
| 图 5 不同图幅范围地图对应不同的Voronoi图 Fig. 5 Different map sheets with different Voronoi diagrams |
改进后的Voronoi图建立后,考虑到点要素对应Voronoi区域面积与局部分布密度成反比的关系,取Voronoi区域面积作为这个层次特征的描述指标,建立相应的信息量模型,得到点状地图的几何分布信息量IG为
式中,si为第i个点要素对应的Voronoi区域面积;s、smax分别为Voronoi区域面积的平均值和最大值。以2为底的对数计算得到的信息量的单位为bit,下同。 4.2 拓扑邻接信息量的度量点要素间的拓扑关系只有两种:相离和相重,若不考虑专题属性,则相重的关系通常没有含义,亦即点状地图的拓扑关系都为相离。进而,可以借助点要素的Voronoi区域间的关系将相离关系进一步区分为一阶邻接、二阶邻接和n阶邻接[17]。这里,邻接程度选择点要素所对应Voronoi区域的一阶拓扑邻接度作为点要素拓扑信息度量的描述指标,并对其进行规范化处理后代入基于特征的信息量模型,可得由拓扑邻接特征产生的点状地图拓扑邻接信息量IT,表达为
式中,ti为第i个点要素对应的Voronoi区域的一阶邻接度;t、tmax分别为点要素对应Voronoi区域一阶邻接度的平均值和最大值。 4.3 聚群结构信息量的度量点状地图上的群体现象相关的知识通过点群结构表达。例如,通过分析病例的聚群结构特征可以了解地域、环境、气候特征与疾病的相关性;提取城市群结构可以研究城市生长规律等。研究点群首先需要提取聚群结构,这通常是通过聚类来实现的。目前,很多学者对空间聚类方法开展了研究[18, 19, 20]。考虑到点群结构内部耦合性强而点群间点要素呈现松散的特点,本文采用基于Delaunay三角网的距离密度约束聚类方法提取点群结构[21]。如图 6所示,点状地图(a)构建Delaunay三角网得到图(b),并聚类得到点群结构的分布图(c),视觉上该结果较好地顾及群内和群间的点要素距离约束,使得群内凝聚程度高而群间凝聚度低。

|
| 图 6 点要素聚类过程 Fig. 6 Clustering of a set of points |
设点状地图经过聚类得到M个点群结构,采用点群结构包含的点要素个数nj、点群分布面积Aj、整体密度Dj作为主要描述参数,3个特征参数的平均值分别为n、A、D。对点群结构描述参数进行规范化处理后,可建立点群结构多样性产生的结构信息量IS,表达为
5 试验与结果分析为了验证本文所提出的空间信息量度量方法的合理性,下面分别用两组点状地图进行试验。
第1组试验截取相同地图范围大小和相同要素数量而分布均匀程度不一的一组数据,如图 7所示(多边形为点要素的改进Voronoi区域)。分别采用本文方法和文献[7]方法计算其信息量,结果列于表 1。从图中可以看出,均匀分布相对简单,而非均匀分布的整体复杂度大,要素的空间分布特征较多元化。这一方面反映在各要素Voronoi区域面积的差异上,在均匀分布情况下,各要素Voronoi区域面积差异较小,而在非均匀分布情况下,各要素Voronoi区域面积差异较大。分析几何分布信息量的计算表达式(2)可知,Voronoi区域面积差异越大,计算得到的几何分布信息量越大。另一方面,均匀分布的点状地图,各点要素间的拓扑邻接特征接近,而非均匀分布的点要素间的拓扑邻接特征差异亦较大。图 7 (b)中各要素的一阶邻接度的差异明显要比图 7 (a)大。由式(3)可知,一阶拓扑邻接度差异越大,计算得到的拓扑邻接信息量越大。此外,从空间认知角度,容易判断图 7 (b)由于点要素间空间距离、拓扑邻接等特征的差异性更大,因而更为复杂多样化,导致包含的信息量更多。从表 1中可以看出,本文方法的计算结果与空间认知结果相一致。同时也发现,文献[7]方法计算得到的信息量结果出现了相反的趋势,即与空间认知结果不一致。因此,本文方法较文献[7]方法更具有合理性。

|
| 图 7 不同空间分布的点状地图 Fig. 7 Two point-shaped maps with different spatial distributions |
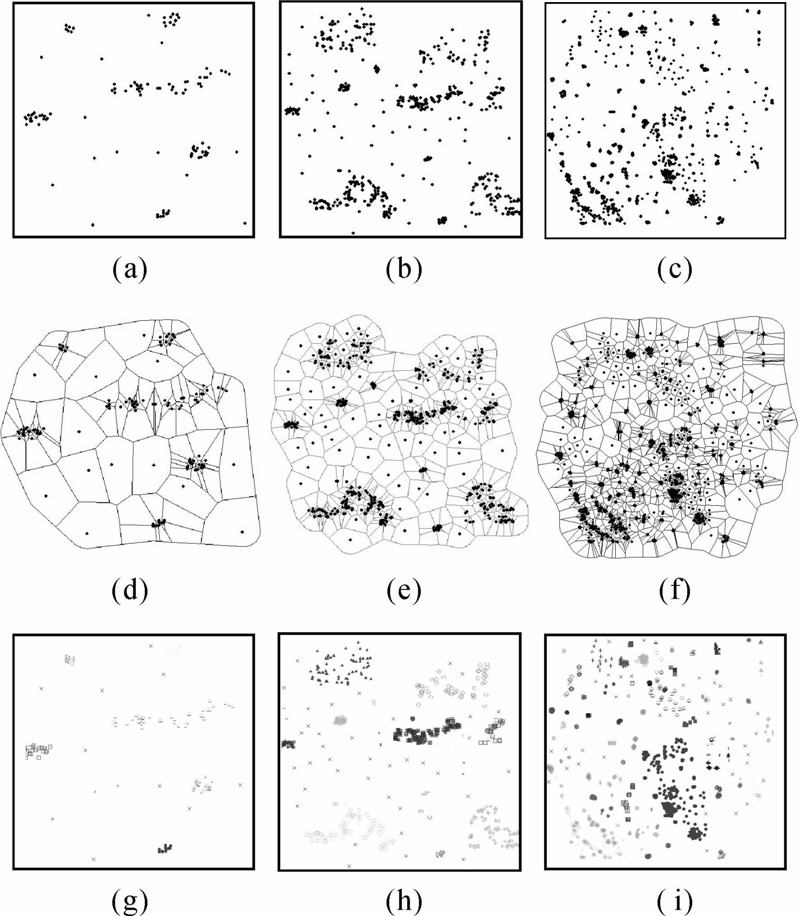
第2组试验的数据源自某疾控部门提供的新生儿低体重病例分布,根据一定范围大小区域内病例数量差异选取了具有代表性的3个区域地图数据,分别如图 8 (a)、(b)、(c)所示。
试验中,首先对原始地图点要素构建约束Voronoi图获得各点要素对应的Voronoi区域,分别如图 8 (d)、(e)、图(f)所示。计算各点要素对应Voronoi区域面积,分别利用Voronoi区域面积和Voronoi一阶邻接度作为特征描述指标,计算地图的几何分布信息量和拓扑邻接信息量。然后根据点要素Voronoi邻接关系建立Delaunay三角网;进而,对三角网的边依次施加整体到局部的统计距离约束,打断三角网中的不一致边(长边或链结构),获得一系列子图;最后,搜索通过三角网边连接的子图,每个子图形成一个空间簇,即空间聚群结构。图 8 (g)、(h)、(i)所示为聚群后的结果,其中未被聚入任一空间簇的点为离群点。对每个聚群结构分别统计其点要素数目、分布面积、分布密度等特征描述指标,即可计算得到点状地图聚群结构信息量。同时,根据文献[7]方法,利用点要素的Voronoi区域面积和Voronoi邻接度计算获得点状地图的几何信息量、拓扑信息量,计算结果列于表 2。
|
| 图 8 分布不等的3组试验数据及对应Voronoi图、聚群结果 Fig. 8 Three groups of experimental data with different spatial distributions |
| bit | ||||
| 包含对象及信息内容 | 图 8 (a) | 图 8 (b) | 图 8 (c) | |
| 点数 | 127 | 616 | 2839 |
| 聚群数 | 6 | 14 | 50 |
| 本文方法 |
|
| 文献[7]方法 |
|
分析表 2中3幅地图的几何分布信息量、拓扑邻接信息量、聚群结构信息量的计算结果,可以得到如下结论。
(1) 随着点要素的增加,3个层次的空间信息量都在逐步增加。随着点要素增多,要素分布也越复杂,不论是从几何分布特征或是拓扑邻接关系特征来看,要素分布的多样性都在逐步增加,点要素Voronoi区域面积、拓扑邻接度的差异性增大,因而包含的几何分布信息量、拓扑邻接信息量越丰富,而形成的各种聚群结构数亦可能随之增加,聚群结构之间包含点要素数目、分布面积、分布密度的多样性或差异性增加,由此聚群结构信息量也逐渐增加。
(2) 随着点要素的增加,几何分布信息量、拓扑邻接信息量随点要素数目增长的速度逐渐变小,这主要有两方面的原因:其一,随着点要素基数的增大,地图信息载负渐趋饱和,因而信息量的增长速度越来越缓慢;其二,地图信息量大小取决于分布多样性程度,不考虑点要素专题属性时,随着点要素基数的增大,要素分布的复杂性程度渐趋平稳,信息量的增长速度将不及点数目的增长速度。
(3) 对于同一幅地图,聚群结构信息量最小;当点要素数目较少时,几何分布信息量较拓扑邻接信息量更大,而当点要素数目偏多时,拓扑分布信息量将超过几何分布信息量。这主要是由于随着点要素的增加,其Voronoi图的拓扑邻接结构关系越来越复杂,对应的拓扑邻接度差异亦增大,因而拓扑邻接信息量增长速度更快。这同时反映了在空间数据管理中拓扑关系维护较几何关系维护更复杂。
(4) 随着聚群结构信息量增长,点要素增长速度越来越快。本试验中,聚群结构是新生儿低体重病例数据空间簇的分布模式,聚群结构信息量丰富,意味着病例分布模式多样化,反映该区域导致新生儿低体重发生的条件更成熟,因而病例发生率偏高。由此,可以通过聚群结构的分布模式,结合地理生态环境等进一步分析疾病诱发因素,采取有效措施进行控制。
对比本文方法与文献[7]方法的计算结果,本文方法计算结果更符合人的视觉感知。文献[7]方法得到区域1的几何信息量和拓扑信息量分别为5.7bit和6.8bit,而区域3的信息量仅有9.2bit和11.4bit,尚且不到区域1的信息量的2倍,凭目视分析这是不合理的。而本文方法计算结果具有更为合理的相对大小趋势。
6 结 论本文深入分析了地图信息的来源和本质特征,剖析点状地图空间信息构成,并将点状地图的空间特征区分为几何分布特征、拓扑邻接特征和聚群结构特征,相应的,将点状地图的空间信息区分为几何分布信息、拓扑邻接信息和聚群结构信息。在此基础上,以基于特征的信息量度量模型为数学基础,通过选取特征度量指标,建立了一套点状地图空间信息量的度量方法。最后,分别以两组地图数据为例,并与比较公认的文献[7]方法对比,试验分析验证了本文所提出的地图信息量度量方法的合理性和优越性。今后的研究将进一步纳入点目标的语义特征来综合考虑地图信息量的度量方法,并尝试运用地图信息度量方法与地图综合、地图信息传输等应用相结合,建立基于地图信息量的地图综合评价方法和渐进式传输方法。
| [1] | SHANNON C E. A Mathematical Theory of Communication [J]. The Bell System Technical Journal, 1948, 27: 379-423,623-656. |
| [2] | KOLCNY′ Cartographic Information: a Fundamental Concept and Term in Modern Cartography [J]. The Cartographic Journal, 1969, 6(1): 47-49. |
| [3] | ZHU Guorui, WANG Jianhua. Research of Some Questions on Modern Cartographic Analysis [J]. Acta Geodaetica et Cartographica Sinica, 1995, 24(1): 77-79. (祝国瑞, 王建华. 现代地图分析有关问题的探讨[J]. 测绘学报, 1995, 24(1): 77-79.) |
| [4] | SUKHOV V I. Information Capacity of a Map: Entropy [J]. Geodesy and Aero Photography, 1967, 10 (4): 212-215. |
| [5] | NEUMANN J. The Topological Information Content of a Map: an Attempt at a Rehabilitation of Information Theory in Cartography [J]. Cartography, 1994, 31(1): 26-34. |
| [6] | BJOKE J T. Framework for Entropy-based Map Evaluation[J]. Cartography and Geographic Information Systems, 1996,23 (2): 78-95. |
| [7] | LI Z L, HUANG P Z. Quantitative Measures for Spatial Information of Maps [J]. International Journal of Geographical Information Science, 2002, 16 (7): 699-709. |
| [8] | HARRIE L, STIGMAR H. An Evaluation of Measures for Quantifying Map Information [J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2010, 65(3): 266-274. |
| [9] | WU H Y, ZHU H J, LIU Y. A Raster-based Map Information Measurement for Qos [C]//Proceedings of ISPRS.[S.l.]:ISPRS,2004:365-370. |
| [10] | CHENG Changxiu, LU Feng, NIU Fangqu. Verification of Raster-based Map Information Measurement [J]. Geo-Information Science, 2006, 8(1): 127-130. (程昌秀, 陆锋, 牛方曲. 栅格地图信息量计算方法的验证分析[J]. 地球信息科学, 2006, 8(1): 127-130.) |
| [11] | LIU Huimin, FAN Zide, DENG Min, et al. A Hierarchical Approach to Measuring the Information Content of the Contours in a Map [J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 777-783. (刘慧敏,樊子德,邓敏,等.地图上等高线信息度量的层次方法研究[J]. 测绘学报, 2012, 41(5): 777-783.) |
| [12] | AI Tinghua, LIU Yaolin. A Method of Point Cluster Simplification with Spatial Distribution Properties Preserved [J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(2): 175-181. (艾廷华, 刘耀林. 保持空间分布特征的群点化简方法[J]. 测绘学报, 2002, 31(2): 175-181.) |
| [13] | JIANG Hao, CHU Yandong, YAN Haowen, et al. Study on Computation of Similarity Relationships of Multi-scale Point Objects [J]. Geography and Geo-Information Science, 2009, 25(6): 1-4. (江浩, 褚衍东, 闫浩文,等. 多尺度地理空间点群目标相似关系的计算研究[J]. 地理与地理信息科学, 2009, 25(6): 1-4.) |
| [14] | MAO Zhengyuan. The Study of Extracting Structure Information of a Clustered Spatial Point Pattern [J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 181-186. (毛政元. 集聚型空间点模式结构信息提取研究[J]. 测绘学报, 2007, 36(2): 181-186.) |
| [15] | YAN Haowen, WANG Jiayao. A Generic Algorithm for Point Cluster Generalization Based on Voronoi Diagrams [J]. Journal of Image and Graphics, 2005, 10(5): 603-606. (闫浩文, 王家耀. 基于Voronoi图的点群目标普适综合算法[J]. 中国图象图形学报, 2005, 10(5): 603-606.) |
| [16] | WHELAN B M, MCBRATNEY A B. Prediction Uncertainty and Implications for Digital Map Resolution[C]//Proceedings of the Fourth International Conference on Precision Agriculture.Madison:[s.n.], 1998: 1185-1196. |
| [17] | CHEN J, ZHAO R L, LI Z L. Voronoi-based K-order Neighbor Relations for Spatial Analysis [J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2004, 59(1): 60-72. |
| [18] | YAN H W, WEIBEL. An Algorithm for Point Cluster Generalization Based on the Voronoi Diagram [J]. Computers and Geosciences, 2008, 34(8): 939-954. |
| [19] | PEI T, JASRA A, HAND D J, et al. DECODE: A New Method for Discovering Clusters of Different Densities in Spatial Data [J]. Data Mining and Knowledge Discovery, 2009, 18(3): 337-369. |
| [20] | DENG Min, LIU Qiliang, LI Guangqiang, et al. Spatial Clustering Analysis and Applications [M]. Beijing: Science Press, 2011.(邓敏, 刘启亮, 李光强,等. 空间聚类分析及应用[M]. 北京: 科学出版社, 2011.) |
| [21] | DENG M, LIU Q L, CHENG T, et al. An Adaptive Spatial Clustering Algorithm Based on Delaunay Triangulation [J]. Computers, Environment and Urban Systems, 2009, 35(4): 320-332. |





