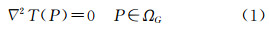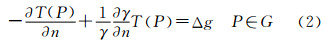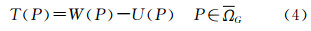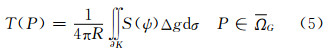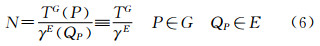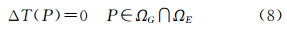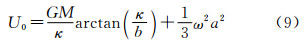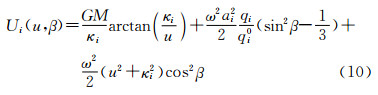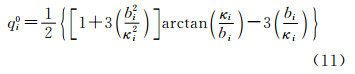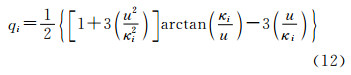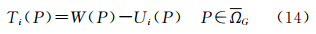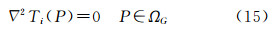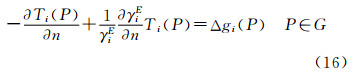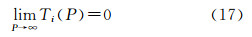2. 武汉大学 测绘遥感信息工程国家重点实验室，湖北 武汉 430079；
3. 地球空间环境与大地测量教育部重点实验室，湖北 武汉 430079
2. Key Laboratory of Information Engineering in Surveying,Mapping and Remote Sening，Wuhan University， Wuhan 430079，China;
3. Key Laboratory of Geospace Environment and Geodesy， Ministry of Edneation，Wuhan University， Wuhan 430079，China
1 引 言
大地水准面是最接近平均海水面的重力等位面[1, 2, 3, 4, 5]，由于它在地球科学研究以及国民经济建设中的重要地位而备受国内外地学科学家的关注，成为物理大地测量领域的研究热点之一。就确定全球大地水准面而言，文献[6]中的方法是目前使用最广、也是最重要的方法之一[2, 5, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17]。斯托克斯方法也称斯托克斯边值问题，其表述如下：在大地水准面G上(见图1)给定重力异常Δg=gP-γQ作为边界值，确定定义在大地水准面上及其外部的、在大地水准面外部调和、在无穷远处正则的扰动位T(P)=W(P)-U(P)，在边界面上满足物理大地测量基本微分方程。这里，gP和γQ分别是大地水准面上P点的重力值和对应于该点的参考椭球(如WGS-84椭球)面上QP点的正常重力值(QP表示Q点随着P点的变化而变化，因而成为P的函数)，W(P)和U(P)分别是地球的重力位和参考椭球产生的正常重力位，后者由4个基本参数确定(见表1)，是已知的。斯托克斯边值问题的数学表述如下：定义在大地水准面G上及其外部空间区域ΩG中的扰动位函数T(P)=W(P)-U(P)满足如下方程
式中，▽2是拉普拉斯算符；n是大地水准面上的外向法线；γ是对应于大地水准面上的P点的参考椭球面上QP点的正常重力值。这里需要指出，扰动位定义在大地水准面上及其外部，即有 式中，ΩG=Ω∪G，表示Ω和G的合集。
|
| 图 1 椭圆线的粗曲线分别表示WGS-84椭球面和大地水准面。斜线填充区(图中Ⅰ)表示大地不准面位于参考椭球面的外部，点填充区(图中Ⅱ)表示大地水准面位于参考椭球面的内部 Fig. 1 The elliptic curve and bold curve denote the surface E of the WGS-84 ellipsoid and the geoid G,respectively. The region filled with slant lines (region Ⅰ) indicates the the geoid is above the ellipsoidal surface,and the region filled by points (region Ⅱ)indicates that the geoid is below the ellipsoidal surface. |
按斯托克斯方法[2, 6, 18],式(1)~(4)的解给出扰动位T(P)(P∈ΩG)的表达式，亦即著名的斯托克斯公式(球面近似)
式中，Δg是重力异常(大地水准面上的重力与相应的参考椭球面上的正常重力之差)；S(ψ)是斯托克斯函数(是已知的)；dσ是球面上的积分面元。有了扰动位，根据布伦斯(Bruns)公式可给出大地水准面差距[2] 它是大地水准面上P点至参考椭球面上QP点(沿正常重力线方向)的距离。在式(6)中，TG(P)≡TG是在大地水准面上P点的扰动位； γE(QP)≡γE是在对应的位于参考椭球面E上的QP点处的正常重力；上标E和G分别表示在参考椭球面上和大地水准面上取值。
要使斯托克斯问题的表述有效，其前提条件是：需要将大地水准面外部的质量去掉或迁移到大地水准面内部[2, 19]，以保证扰动位在大地水准面外部调和。为了满足这一要求，最常用的方法 是Helmert第二凝聚法[8, 9, 11, 12, 15, 18, 19, 20, 21, 22, 23]，亦即将大地水准面外部的质量沿大地水准面法线方向移到大地水准面以下21 km的层面上。因此，本文所讨论的前提是：大地水准面外部的质量已经移到了大地水准面内部，比如，采用Helmert第二凝聚法。
| 基本参数 | a/m | f | GM/108m3 s-2 | ω/10-11rad·s-1 | 导出参数 | |
| b/m | U0/m2 s-2 | |||||
| WGS-84椭球 | 6 378 137 | 1/298.257 223 563 | 3 986 004.418 000 000 00 | 7 292 115 | 6 356 752.314 24 | 62 636 851.714 6 |
| 内部椭球 | 6 377 987 | 1/ 298.261 243 404 | 3 986 004.418 000 000 00 | 7 292 115 | 6 356 603.105 37 | 62 638 318.801 4 |
| 二者差异 | 150 | 4.518 778 778×10-8 | 0 | 0 | 149.208 87 | 1 467.086 8 |
斯托克斯方法本身有不少人们熟知的缺陷，比如：将大地水准面外部的质量移到大地水准面内部之后，会改变重力场以及大地水准面的位置，因此需要做二次调整；要将大地水准面外部的质量移到大地水准面内部，需要知道地面点的海拔高，如此才能将大地水准面外部的质量全部移到大地水准面内部，但如果知道了海拔高，也就不再需要求解斯托克斯问题来确定大地水准面了，因为知道了海拔高就等于知道了大地水准面；等其他缺点。上述缺陷不是本文讨论的范畴。本文讨论的是人们尚未意识到的存在于斯托克斯方法中的理论性困难。
首先，在斯托克斯理论中，地球的重力位W(P)仅仅定义在大地水准面和大地水准面外部的合集ΩG=ΩG∪G之中(见图1和图2)，这是因为质量调整以后，地球内部的密度分布改变了，已经不需要知道地球内部的密度分布了(实际上也不可能精确知道)；而正常重力位U(P)仅仅定义在参考椭球面E及其外部空间ΩE的合集ΩE=ΩE∪E之中，这是因为正常重力位由4个基本参数(见表1)确定，不涉及椭球内部的密度分布，即不同的密度分布可产生同样的外部正常重力位，这也表明正常重力位U(P)在参考椭球内部没有定义。于是，扰动位T(P)=W(P)-U(P)仅仅定义在既属于ΩG又属于ΩE的交集ΩG∩ΩE之中，换言之，有如下方程
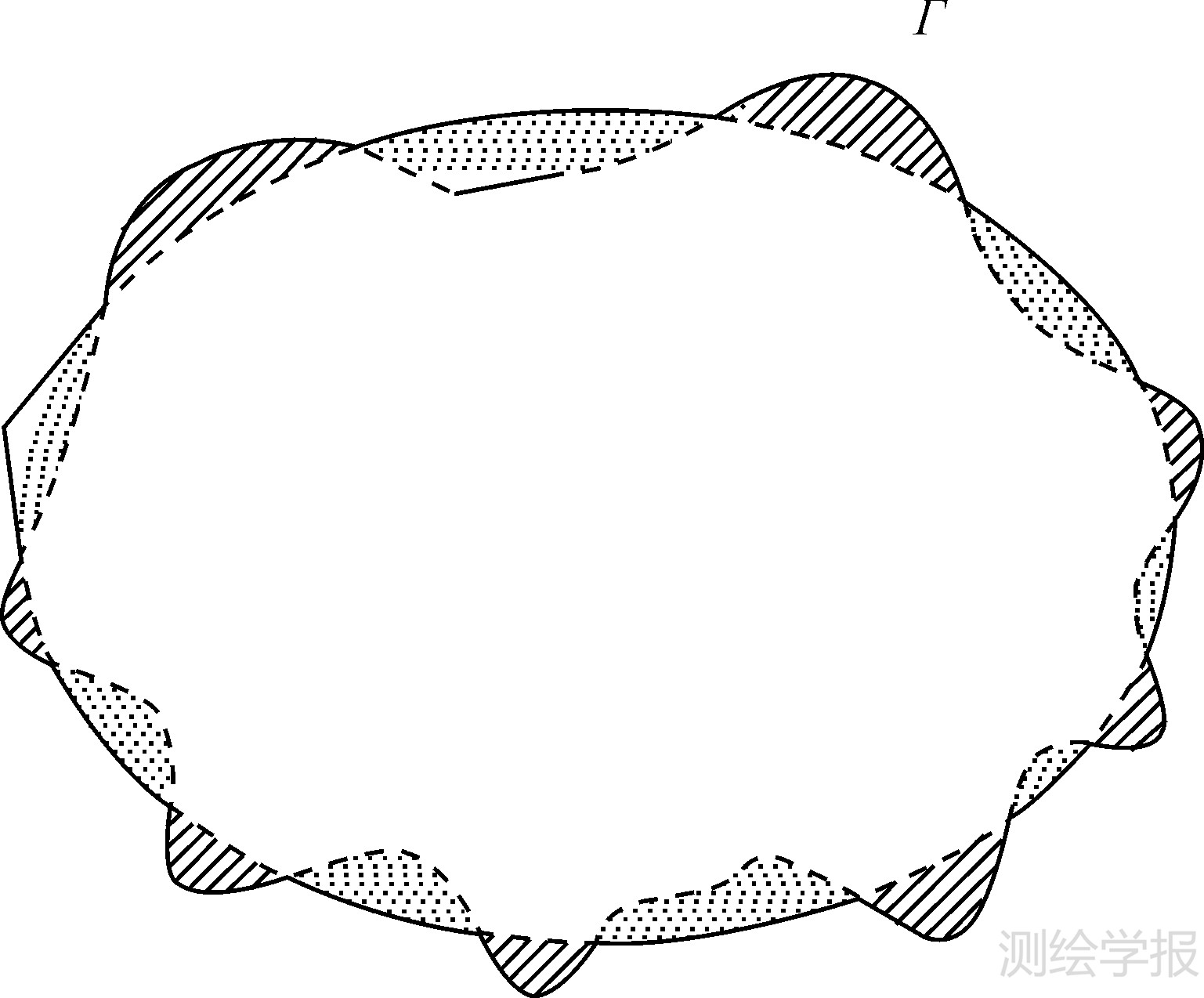
因此，T(P)不仅需要在大地水准面外部调和，而且需要在参考椭球(比如，取WGS-84椭球为例)外部调和，亦即，T(P)仅仅在区域ΩG∩ΩE之中调和(见图2)。因此，式(1)应该由式(8)代替
|
| 图 2 粗曲线(Γ)由位于参考椭球外部的大地水准面部分、位于大地水准面外部的参考椭球面部分以及二者的重合部分构成 Fig. 2 The bold curve (Γ) denotes the boundary that consists of the parts of the geoid above the ellipsoidal surface,the parts of the ellipsoidal surface above the geoid,and the parts that the geoid coincide with the ellipsoidal surface |
这里需要进一步指出，由于确定正常重力位时只用到了4个基本参数，并通过求解外部边值问题确定了外部调和场[2, 3]，因此，其定义域只能是椭球的外部，亦即在参考椭球内部没有定义，当然也就谈不上调和了。实际上，的确存在某种内部分布(如本文提出的更小的椭球)，由此可产生正常场，但这个正常场需要根据内部椭球参数及内部椭球边界来确定，而如此确定的正常场已经不是通常意义上采用的正常场了。
参考椭球的选取，总是以使得它与大地水准面符合得最好为原则，于是，必定会出现如下图景：大地水准面的一些部分位于参考椭球面的上方(外部)，而另外一些部分则位于参考椭球面的下方(内部)，如图1所示。实际上，只要考察一下EGM96大地水准面[24]或EGM2008大地水准面[25]即可证实这 一点。因此，区域ΩG∩ΩE小于区域ΩG。
令Γ表示ΩG∩ΩE的内部边界(见图2)，则Γ由部分大地水准面和部分参考椭球面组成，确切地说，Γ由位于参考椭球面上边的大地水准面部分、位于大地水准面上边的参考椭球面部分、以及它们的重合部分组成。
其次，由于部分大地水准面位于参考椭球内部，因此，扰动位T(P)=W(P)-U(P)并非在整个大地水准面上及其外部有定义，因为正常重力位U(P)在参考椭球内部没有定义。即式(2)和(4)不能成立，因为T(P)只在ΩG∩ΩE(其边界为Γ)中有定义，而ΩG∩ΩE小于ΩG。
按传统的斯托克斯理论，式(1)、(2)和(4)实际上均不能成立，这就是尚未被人们关注的斯托克斯方法中存在的理论性困难。
下面给出一种方法，可以消除上述理论性困难。
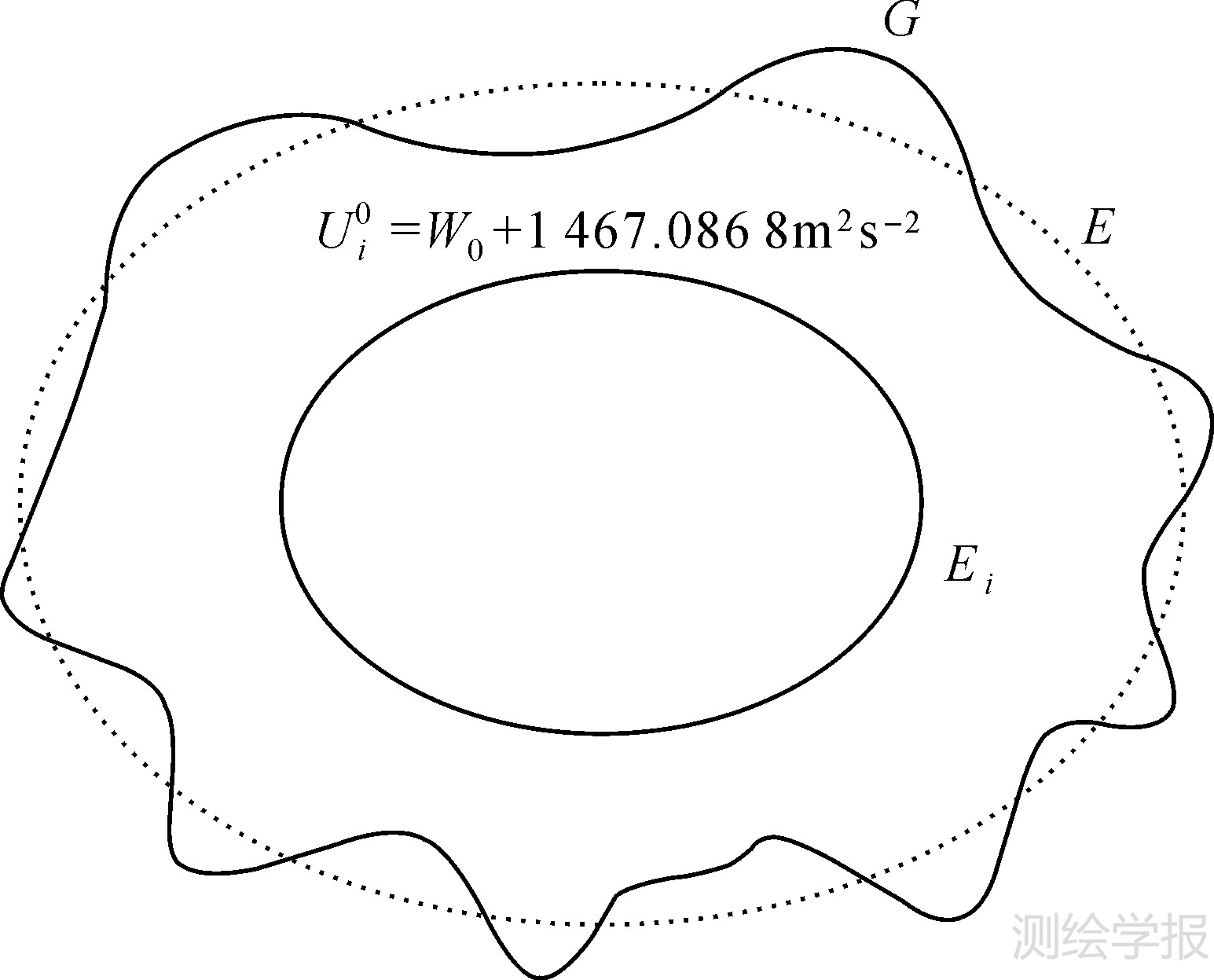
3 改进的斯托克斯方法选取一个内部参考椭球(简称内部椭球)，其中心与WGS-84椭球的中心重合见图3，在内部椭球的边界Ei上取值Ui0=W0+1 467.086 8 m2s-2，其他参数见表1。实际上，需要如此选取内部椭球，使得由内部椭球产生的新的正常重力位场Ui(P)在WGS-84椭球面上正好等于大地水准面上的常数，即W0=U0(在精度要求范围内)。于是，新的扰动位Ti(P)=W(P)-Ui(P)在ΩG中调和。只要将式(1)~(4)中的T(P)=W(P)-U(P)换成Ti(P)=W(P)-Ui(P)，传统的斯托克斯方法中的理论性困难就不复存在。
|
| 图 3 改进的斯托克斯方法。椭圆形虚线(E)，不规则曲线(G)和椭圆形实线(Ei)分别表示WGS-84椭球，大地水准面，和内部椭球 Fig. 3 Modified Stokes’ approach. The dashed elliptic curve irregular curve and solid elliptic curve denote the surface E of the WGS-84 ellipsoid,the geoid G,the surface Ei of the inner ellipsoid，respectively |
考察EGM2008大地水准面[25]会发现，大地水准面差距的绝对值不超过120m。因此，内部椭球的长半轴可选为ai=a-150，其中，a是地球赤道平均半径。至于其他3个基本参数，GMi、fi和ωi(分别表示内部椭球地心常数、扁率和旋转角速度),其中的两个，GMi和ωi，与WGS-84椭球的相同，即GMi=GM,ωi=ω；而另外一个，也即fi，应该如此选择，使得在WGS-84椭球面上，由内部椭球产生的新的正常重力位Ui(P)|E正好等于WGS-84椭球产生的正常重力位U(P)|E，即Ui(P)|E=U(P)|E=W0。这一点是可以实现的，后面的数值计算将予以证实。
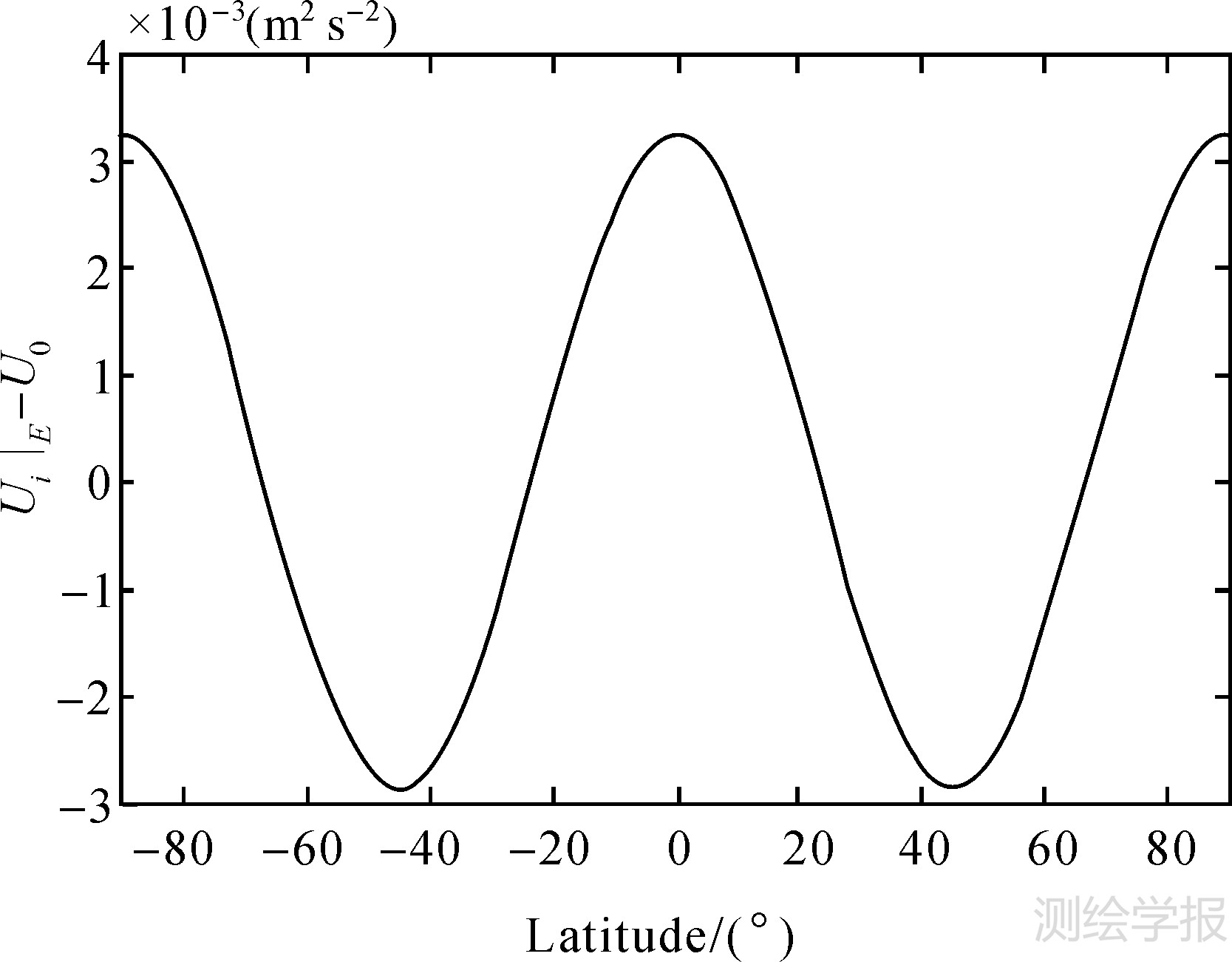
在内部椭球面上，新的正常重力位为Ui0=62 638 318.801 4 m2s-2(见表1)，它比W0大1 467.086 8 m2s-2,也即Ui0=W0+1 467.086 8 m2s-2。 如此，新的正常重力位在WGS-84椭球面上的值正好是U0=W0=62 636 851.714 6 m2s-2(在±0.3 mm精度范围，见表2和图4)
| 10-3m2s-2 | |||
| 最大值 | 最小值 | 平均值 | 标准差 |
| 3.27 | -2.86 | 0.207 | 2.16 |
|
| 图 4 新的正常重力位Ui在WGS-84椭球面上的值(Ui|E)与常数U0=W0之间的差异 Fig. 4 The distribution of the differences between the values (Ui|E) of the new normal gravity potential Uion the surface of the WGS84 ellipsoid and the constant U0=W0 |
需要指出，U0与GM由式(9)关联[2]
其中，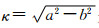
是线偏心率(linear eccentricity)。
下面阐述理论基础。
理论上，要求由内部椭球产生的新的正常重力位在内部椭球面上保持恒定值Ui0，于是，可利用熟知的正常椭球公式来表示内部椭球外部的新的正常重力位场Ui(P)。将Ui0取得比W0大一些，使得Ui(P)在WGS-84椭球面上正好等于W0(在精度范围内，比如±0.3 mm)。这样，仍然可以利用与斯托克斯方法完全相同的一套方法来确定大地水准面。
在内部椭球面及其外部，新的正常重力位由式(10)给出[2]
其中，
，是线偏心率;ai、bi、ω、GM是内部椭球的4个基本参数(见表1)；u是椭球坐标(u,θ,λ)的第一分量；β是归化纬度[2]；qi0和qi由式(11)、(12)定义
在内部椭球面Ei上,Ui(u,β)的值可表示为
基于式(10)~(13),利用数值计算，可确定bi(或fi)以及Ui0，见表1。在精度范围(±0.3 mm) 内，新的正常重力位Ui(P)在WGS-84椭球面上等于W0，结果如图4和表2所示。
新的扰动位Ti(P)由式(14)定义
它在ΩG中调和
仿效文献[2]的推导方法,可立即得到物理大地测量基本微分方程
式中，新的重力异常Δgi(P)是大地水准面上P点的重力值与对应的WGS-84椭球面上QP点的新的正常重力值之差；γiE是WGS-84椭球面上的新的正常重力值；n是大地水准面上的外部法线；新的扰动位Ti(P)同样满足正则条件
基于式(15)~(17),采用传统的方法[2],即可根据在大地水准面上给定的重力异常Δgi(P)确定出扰动位Ti(P)，进而根据Bruns公式确定出大地水准面差距
式中，TiG和γiE分别是在大地水准面上的新的扰动位和WGS-84椭球面上的新的正常重力值；Ni是新的大地水准面差距，它是WGS-84椭球面上的QP点沿新的正常重力线至大地水准面上P点的距离。
改进的斯托克斯方法与传统的斯托克斯方法的差异在于：改进方法中涉及的量(如TiG，γiE，Ni等)，均与内部椭球产生的新的扰动位场Ui发生关联，因而相关的量也冠以“新的”；而在传统方法中，相关的量(如TG，γE，N等)与WGS-84椭球产生的正常重力位场U(P)发生关联。由于在WGS-84椭球面上及其外部，Ui与U完全重合(在精度要求范围内)，因此，在目前的精度水平下，用新的场计算的相关量与传统方法得到的完全一致。
改进方法有两个优势：① 作为一种参考面，传统的WGS-84椭球参考面仍然可以采用，因此，在新的框架中，传统的相关计算公式(以及各种协议)仍然可以使用，但赋予了新的含义；② 由于新的正常重力位Ui(P)在整个内部椭球的外部有定义，而内部椭球又位于大地水准面的内部，因此，传统的斯托克斯方法中存在的理论性困难就消失了。确切地说，采用改进的斯托克斯方法，不仅消除了传统斯托克斯方法中存在的理论困难，而且不影响所有与传统斯托克斯理论相关的计算公式。
4 讨论与结论通常，处理扰动位场T=W-U比处理重力位场W(或引力位场V)要容易得多，因此，在物理大地测量学领域，科学家主要研究如何确定扰动位场，其基本要求是扰动位在边界面(如大地水准面)外部调和，然后根据不同的边界条件确定扰动位。以确定大地水准面为目的，最有代表性的方法是斯托克斯方法[2, 5, 6]。需要指出，为了克服斯托克斯方法存在的缺陷，在20世纪中叶，出现了Molodensky方法[26, 27]，但由此确定的是似大地水准面而不是大地水准面。由于似大地水准面不是重力等位面，其应用价值受到了限制。
斯托克斯方法本身的主要目的是确定大地水准面以及外部重力场。不过，由于该方法的前提是需要将大地水准面外部的质量迁移到大地水准面内部，因此会改变大地水准面以及外部重力场。由于确定地球外部重力场有更好的方法，亦即人们熟知的球谐展开法，因此，利用斯托克斯方法确定重力场的功效已不再被大地测量学家所采用。另一方面，由于人们还没有找到更好的确定全球大地水准面的方法，因此，确定大地水准面的斯托克斯方法仍然被人们普遍采用。
就斯托克斯方法而言，边界是大地水准面，基于给定的边界上的重力异常确定外部扰动位场T。理论性困难在于，当大地水准面位于参考椭球(WGS-84椭球)内部时，T在大地水准面与参考椭球之间的区域没有定义，因而更谈不上调和，而“有定义”和“调和性”是斯托克斯理论的基本要求。为了消除斯托克斯方法存在的理论困难，本文提出了改进的斯托克斯方法。基于改进的斯托克斯方法，新的正常重力位场由内部参考椭球产生，该正常场在内部椭球的外部有定义、调和，而且在WGS-84椭球面上正好等于大地水准面上的重力位。于是，改进的斯托克斯方法不仅消除了传统斯托克斯方法中存在的理论性困难，而且，传统的涉及斯托克斯方法的一套公式均可使用。就目前的精度水平而言，改变的只是观念。
那么，为什么传统的斯托克斯方法中的一套公式可以继续使用呢？原因如下所述。
传统上，正常重力位U由WGS-84椭球产生，其表达式类似于式(10)。但可以设想，该场是由一个内部椭球产生的，如文中所给定的场式(10)。这时，该场在大地水准面与WGS-84椭球面之间又有定义了。由此，在具体应用(或计算)时，当大地水准面位于WGS-84椭球外部时，正常重力位是由WGS-84椭球产生的，计算没有任何问题；但当大地水准面位于WGS-84椭球内部时，原本无法计算由WGS-84椭球产生的正常重力位，因为它在椭球内部根本没有定义，然而幸运的是，这时的正常重力位可以认为是由位于WGS-84椭球内部的一个内部椭球产生的。确切地说，人们偷换地使用了内部椭球产生的正常重力位，但没有意识到。没有意识到，是因为WGS-84椭球产生的正常重力位的计算公式，可以在其内部计算(不产生奇异)，其计算值恰似一个内部椭球产生的值(在精度范围内)。这的确是一个巧合。正是这种巧合，使得人们无需改变现有的、传统的斯托克斯方法中的一整套计算公式。但需要改变的是观念。
致 谢: 由于长期亲聆宁津生院士教诲，收益良多，特撰写此文，表达我对宁老的感谢和敬意。同时还要感谢李进博士和韩建成博士对本文的支持。| [1] | GRAFAREND E W. What is a Geoid?[C]//Geoid and Its Geophysical Interpretations.London:CRC Press, 1994. |
| [2] | HEISKANEN W A, MORITZ H. Physical Geodesy[M]. San Francisco: Freeman and Company, 1967. |
| [3] | HOFMANN W B, MORITZ H. Physical Geodesy[M]. 2nd Ed. Wien: Springer, 2005. |
| [4] | SHEN Wenbin, NING Jinsheng, LI Jiancheng, et al. On the Geoid[J]. Journal of Wuhan University, 2003, 28(6): 683-687. (申文斌, 宁津生, 李建成, 等. 论大地水准面. [J] 武汉大学学报:信息科学版, 2003, 28(6): 683-687.) |
| [5] | CHAO Dingbo, SHEN Wenbin, WANG Zhengtao. Investigations of the Possibility and Approach for Determining the Centimeter-level Global Geoid[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(4):370-376. (晁定波, 申文斌, 王正涛. 确定全球厘米级精度大地水准面的可能性和方法探讨[J]. 测绘学报, 2007, 36(4):370-376). |
| [6] | STOKES G G. On the Variation of Gravity at the Surface of the Earth[J]. Transactions of the Cambridge Philosophical Society, 1849(8): 672-695. |
| [7] | WONG L, GORE R. Accuracy of Geoid Heights from Modified Stokes Kernels[J]. Geophysical Journal. Royal Astronomical Society , 1969(18): 81-91. |
| [8] | VAN͡CEK P, KLEUSBERG A. The Canadian Geoid—Stokesian Approach[J]. Manus Geodesy, 1987(12): 86-98. |
| [9] | VAN͡CEK P, MARTINEC Z. Stokes-Helmert Scheme for the Evaluation of a Precise Geoid[J]. Manus Geodesy, 1994(19):119-128. |
| [10] | VAN͡CEK P, NAJAFI M, MARTINEC Z, et al. Higher Degree Reference Field in the Generalized Stokes-Helmert Scheme for Geoid Computation[J]. Journal of Geodesy, 1996(70):176-182. |
| [11] | MARTINEC Z. Boundary-value Problems for Gravimetric Determination of Precise Geoid[C]//Lecture Notes in Earth Sciences. Berlin:Springer, 1998. |
| [12] | SJÖBERG L E. On the Topographic Effects by the Stokes- Helmert Method of Geoid and Quasi-geoid Determinations[J]. Journal of Geodesy, 2000(74): 255-268. |
| [13] | SJÖBERG L E. The Effect of Downward Continuation of Gravity Anomaly to Sea Level in Stokes Formula[J]. Journal of Geodesy, 2001(74): 796-804. |
| [14] | SJÖBERG L E. A Solution to the Downward Continuation Effect on the Geoid Determined by Stokes Formula[J]. Journal of Geodesy, 2003(77): 94-100. |
| [15] | ELLMANN A, VANÍ ČEK P U. Application of Stokes-Helmert’s Approach to Geoid Model Computation[J]. Journal of Geodesy, 2007(43): 200-213. |
| [16] | XU Xi, ZHU Jianjun. Relative Accuracy Estimation of the Regional Gravimetric Geoid[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(5):383-390. (许曦, 朱建军. 区域重力大地水准面确定的相对精度估计[J]. 测绘学报, 2009, 38(5):383-390.) |
| [17] | LI Fei, CHEN Wu, YUE Jianli. GPS Applications in Physical Geodesy and GPS Boundary-value Problem[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(3):198-203. (李斐, 陈武, 岳建利. GPS在物理大地测量中的应用及GPS边值问题[J]. 测绘学报, 2003, 32(3):198-203.) |
| [18] | GUAN Zelin, NING Jinsheng. Figure of the Earth and Its External Gravity Field[M]. Beijing:Surveying and Mapping Press, 1981. (管泽霖,宁津生. 地球形状及其外部重力场[M]. 北京:测绘出版社,1981.) |
| [19] | RAPP R H. Use of Potential Coefficient Models for Geoid Undulation Determinations using a Spherical Harmonic Representation of the Height Anomaly/Geoid Undulation Difference[J]. Journal of Geodesy, 1997(71): 282-289. |
| [20] | MORITZ H. On the Use of the Terrain Correction in Solving Molodensky’s Problem[R]. Ohio :Ohio State University, 1968. |
| [21] | WANG Y M, RAPP R H. Terrain Effects on Geoid Undulation Computations[J]. Manus Geodesy, 1990(15): 23-29. |
| [22] | MARTINEC Z, MATYSKA C, GRAFAREND E W, et al. On Helmert’s 2nd Condensation Method[J]. Manus Geodesy, 1993(18): 417-421. |
| [23] | HECK B. On Helmert’s Methods of Condensation[J]. Journal of Geodesy, 2003(77): 155-170. |
| [24] | LEMOINE F G, KENYON S C, FACTOR J K, et al. The Development of the Joint NASA and NIMA Geopotential Model EGM96[R]. Maryland: NASA Goddard Space Flight Center, 1998. |
| [25] | PALVIS N K, HOLMES S A, KENYON S C, et al. An Earth Gravitational Model to Degree 2160: EGM2008[R]. Vienna :EGU General Assembly, 2008. |
| [26] | MOLODENSKY M S, EREMEEV V F, YURKINA M I. Methods for Study of the External Gravitation Field and Figure of the Earth[M]. Jerusalem,[s.n.], 1962. |
| [27] | MORITZ H. Adwanced Physical Geodesy[M].Karlsruhe: Herbert Wichman,1980. |