2. 武汉大学 测绘学院,湖北 武汉 430079
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China
1 引 言
目前全球解GPS坐标时间序列可以量测到小于1 mm的变形,成为探测构造运动、冰后回弹等导致的地壳长期或者季节性变形的重要手段[1, 2, 3, 4, 5]。GPS数据处理中由于误差具有多源、多样性,模型残差随着法方程的求解传播到了坐标中,与表征GPS测站真实运动信号相互混合,加大了解释GPS坐标时间序列中的各类信号的难度。造成测站时间序列中运动信号的因素包括两类:其一是变形信号,包括测站真实运动以及外部未模型化的地球物理效应;另一类为与GPS技术相关的未识别误差,包括由于多路径、对流层、高阶电离层、轨道误差等模型残差引入的虚假信号。文献[6]认为全球解GPS时间序列中的周年信号仅有40%可用真实的地表负荷模型来解释。文献[7]则认为时间序列中的非线性变化主要由地球物理信号产生,而非与技术相关的噪声。Meisel研究了测站的年周期信号振幅以及对线性速度估值的影响,结果表明,多数测站高程分量的年周期振幅为4~6 mm,很大一部分测站的振幅超过1 cm。文献[8]认为地球物理流体质量负载的再分布可以解释不到一半的非线性变化,残余的大部分变化可能由未识别的GPS技术误差及分析策略引起。
对于GPS短基线而言,由于采用双差观测值进行参数估计,固体潮、海潮模型误差,电离层误差、轨道误差、残余的对流层等均削弱到可以忽略的程度,仅有与测站相关的误差如多路径影响、天线相位中心等可能成为时间序列中的伪信号主要来源[9]。如果测站观测墩、天线等硬件完全一致,则天线相位中心模型误差亦可以忽略。此时,仅有多路径误差由于其严重依赖于观测条件、天线的性能(抑制多路径)等外部因素可能残留在坐标时间序列中,因此,确认短基线时间序列中多路径的影响是否存在且有效的评估量级,是分析并正确解释测站运动的前提。本文计算西龙池上水库5个连续运行站的近2年的观测数据,获得了各监测站的坐标时间序列,分析并评估了短基线中多路径效应的影响,确定了西龙池水库各监测点的长期变形趋势。
2 GPS数据处理5个监测点和1个基准点分布如图 1所示,其中监测点L022、S191、S171、L132、S071分别位于环库断面上,其中L022位于水库主坝体上,L132位于水库副坝体上,S071位于主坝体东向断面上,基准点TN02、TN01位于在水库东面的稳定点上,基准站与监测站之间的基线距离为200~600 m,各监测站均建在特制的观测墩上且观测条件好,仰角8°以上没有遮挡,其中基准站观测墩直接打入基岩上,各测站采用TRIMBLE NETRS接收机、CHOKE RING天线(TRM29659.00)进行全天候24 h不间断观测。
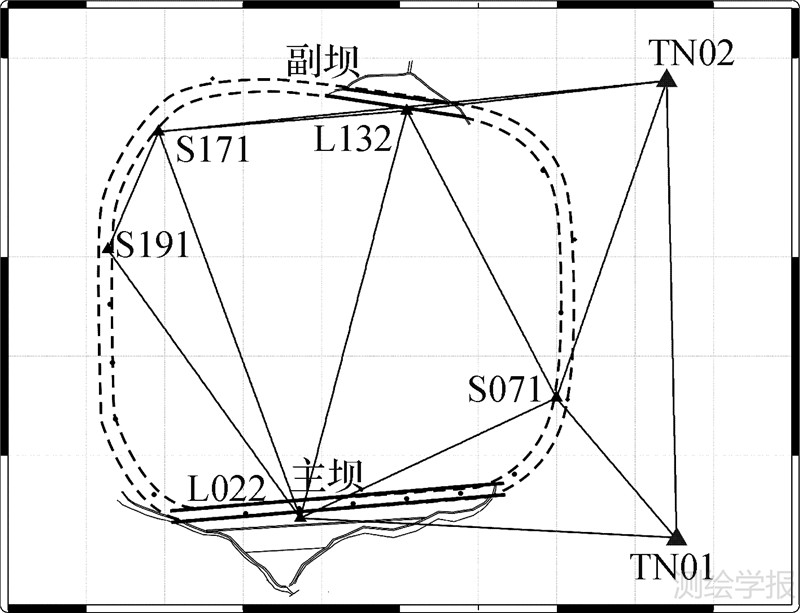
|
| 图 1 测站点位分布图 Fig. 1 Location of sites served as reference stations and monitoring stations in Xilongchi GPS monitoring system |
本文中GPS数据跨度为2009-07-11—2011-06-28,采样率为5 s,观测数据采用DDMS①软件进行参数估计。基线解算的主要策略为:① 采用4 h时段解处理模式;② 因为载波相位观测值L1的噪声仅为LC的1/3,故采用L1进行坐标估计;③ 不附加参数估计测站天顶对流层延迟;④ 忽略固体潮、海潮模型改正;⑤ 卫星轨道采用广播星历;⑥ 模糊度分离与固定采用网解模式,即固定同步网中的独立双差模糊度;⑦ 将基准站TN02的坐标固定为精确已知坐标,以提供起算坐标和基准;⑧ 采用与高度角相关的绝对天线相位中心改正(PCV)模型,忽略方位角的影响。为了分析多路径效应对结果时间序列的影响,对同样的数据分别采用15°、25°截止高度角进行处理。
① DDMS(Dam Deformation Monitoring Software)是自主开发的大坝变形GPS监测软件。
3 监测点坐标时间序列坐标时间序列的如图 2示,绿色点表示采用15°截止高度角计算结果,蓝色点表示采用25°截止高度角计算结果,L132、S191测站时间序列中的阶跃(红色线),主要是由于更换天线导致。在2009-11-15附近,测站L132、S171、S191均出现了较为明显地跳变,尤其在N分量达8~10 mm,之后又逐渐回弹趋于平稳。通过对该时期气象信息比对,发现2009年11月中旬,西龙池上水库库区发生了特大暴雪,推测积雪覆盖天线罩影响了卫星的瞬时天线相位中心,因此,剔除序列中上述期间的数据。
总体上讲,各监测站时间序列主要呈现出如下特征:① 2009年7月至2011年6月期间西龙池上水库已完成初次蓄水后,水库整体上较为稳定,除S071东西方向外,各监测点平面方向波动范围为-3 mm~3 mm,垂直方向为-5 mm~5 mm;② 部分监测点的N、E分量上出现了明显的线性运动趋势,其中主坝上监测点L022存在明显的向东运动;③ 5个监测站均出现了不同程度的下沉,其中L022、L132较为明显;④ 部分监测站在N、E分量呈现了微弱的周期运动信号。
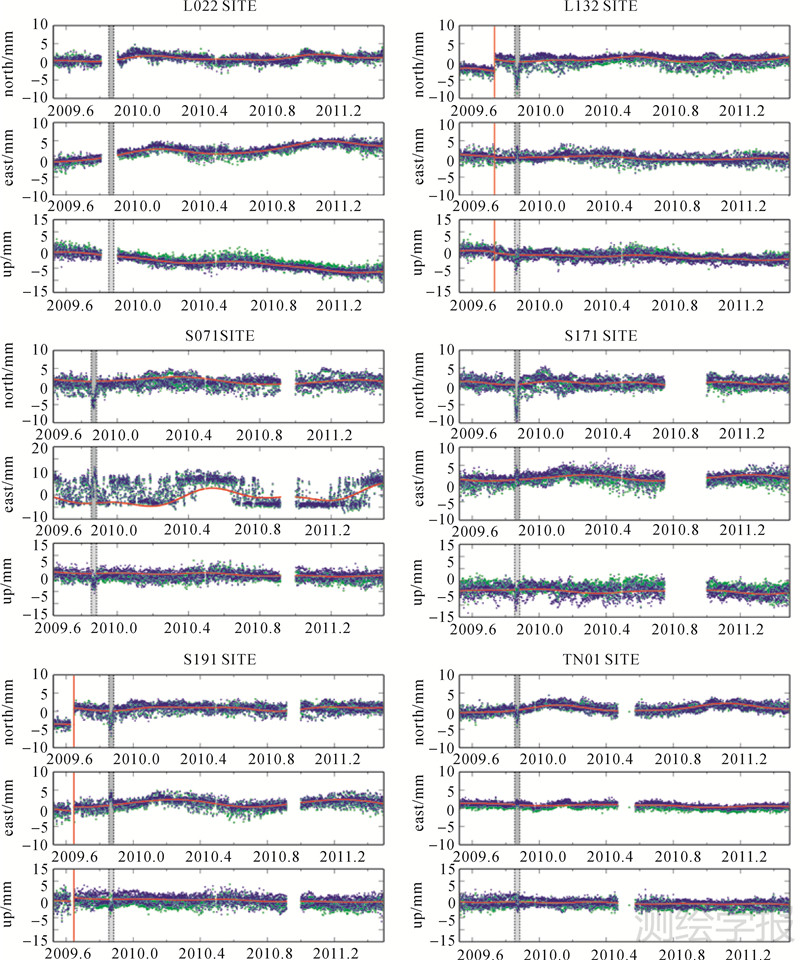
|
| 图 2 监测站坐标时间序列 Fig. 2 Changes in coordinate time series for the monitoring stations |
部分学者的研究表明GPS短基线时间序列中存在周年运动信号。文献[10]分析了10 m、100 m、1 km的短基线时间序列,序列中存在微弱的周年信号,其振幅为水平方向0.05~0.24 mm,垂直方向0.04~0.60 mm。文献[1]利用TRACK软件分析数据跨度为数年的10条短基线(<200 m)时间序列,其中有6条基线出现了振幅大于0.5 mm的周年信号,有2条基线甚至超过了2.5 mm。文献[11]利用模拟的多路径反射源,计算了多路径延迟误差对数年的IGS站坐标时间序列影响,发现其可能为测站的GPS坐标序列中引入线性、周年信号以及系统偏差。对于本文中的坐标时间序列,由于采用双差观测值进行坐标估计,一定程度上削弱多路径效应的影响,同时多路径效应的影响与卫星的高度角有关,当卫星的高度角较小时,多路径效应的影响较为明显。因此,为了评估多路径效应对时间序列中的影响,本文分别采用15°、25°的截止高度角对相同数据进行了处理,统计结果如表 1所示。
| mm | ||||||||||||
| 测站 | N | E | U | |||||||||
| max | min | ave | RMS | max | min | ave | RMS | max | min | ave | RMS | |
| L022 | 1.8 | -1.4 | 0.0 | 0.4 | 2.0 | -0.7 | 0.3 | 0.3 | 3.3 | -4.0 | -0.6 | 0.8 |
| L132 | 2.0 | -3.1 | 0.4 | 0.3 | 2.0 | -0.8 | 0.3 | 0.3 | 3.6 | -6.5 | -0.4 | 1.0 |
| S071 | 1.5 | -2.1 | 0.1 | 0.4 | 1.6 | -1.6 | 0.3 | 0.3 | 4.8 | -4.7 | 0.7 | 1.0 |
| S171 | 2.9 | -3.0 | 0.4 | 0.5 | 2.6 | -1.5 | 0.7 | 0.5 | 4.5 | -5.2 | -1.1 | 1.8 |
| S191 | 2.7 | -2.7 | 0.0 | 0.4 | 2.7 | -0.9 | 0.3 | 0.2 | 4.8 | -4.1 | 1.0 | 1.0 |
| TN01 | 1.1 | -1.2 | 0.1 | 0.4 | 1.2 | -0.5 | 0.5 | 0.6 | 1.4 | -1.2 | 0.5 | 0.8 |
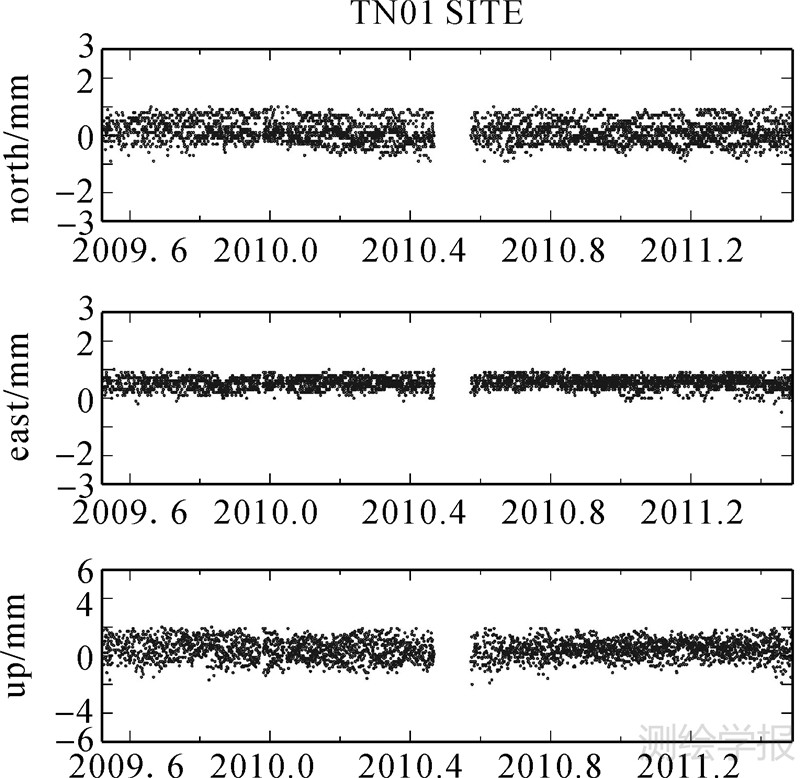
|
| 图 3 TN01测站15° 25°截止高度角计算坐标序列差值 Fig. 3 Difference sequence between solutions for 15°and 25°elevation cutoff angle for stations TN01 |
可以看出分别采用15°、25°的截止高度角进行处理,监测点坐标时间序列存在系统性偏差,平面方向为~0.5 mm,高程方向为~1 mm,序列的差值RMS分别为~0.5 mm、~0.5 mm、~1.0 mm。其中基准站TN01的差异最小,S171差异最大。如图 2所示。TN01、S171坐标时间残差序列中未见明显的周期信号,可见采用不同的截止高度角,监测站坐标时间序列中的周期信号没有明显的变化,多路径效应的影响并非监测站时间序列中的周期信号的主要来源。其中,TN01、L022站较其余监测站残差序列RMS小,主要是由于TN02、L022离水库水面远,而其余监测站如S171位于近水侧岸边,水面反射导致的多路径影响相对较大,与TN01相比,图 2所示的S171差值序列中呈现的N、E方向微弱的线性趋势以及U方向的周期信号,可能由于多路径效应引起的。
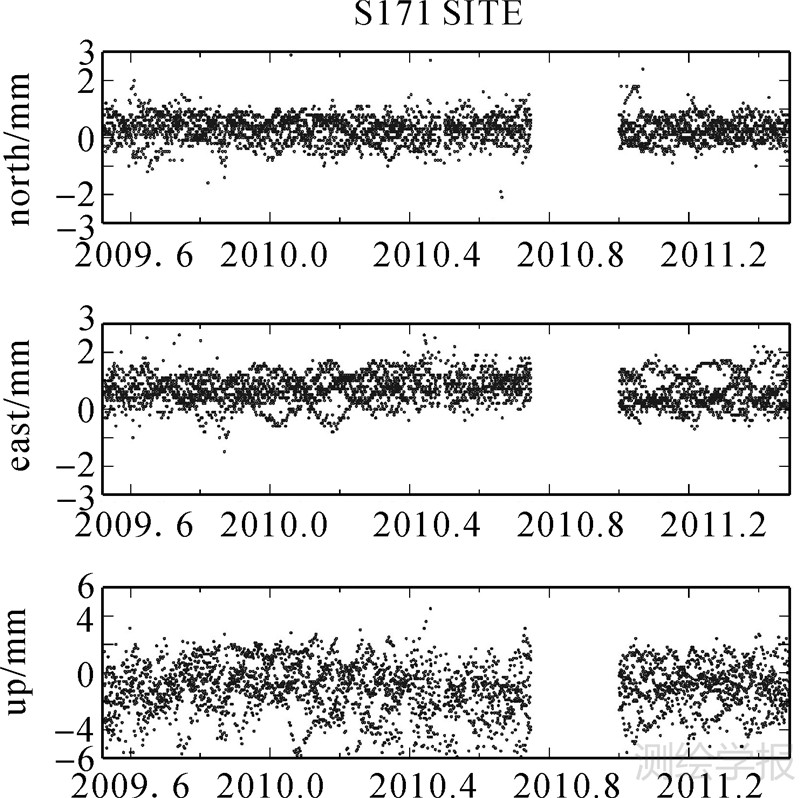
|
| 图 4 S171测站15° 25°截止高度角计算坐标序列差值 Fig. 4 Difference sequence between solutions for 15°and 25°elevation cutoff angle for stations S171 |
全球解GPS坐标时间序列中存在周年波、半周年波、周日(S1)波、半周日(S2)波以及~K1,~K2波。其中~K1波周期为GPS卫星星座的重复周期。本文在对时间序列拟合以确定长期变形时,仅考虑周年波、半周年波,使用CATS[12]软件进行参数估计,CATS采用MLE(mximum likelihood estimate)估计时间序列中的线性部分(斜率、截距,阶跃)、周期项(周年信号的振幅,相位)以及噪声模型(幅度、谱指数)等。
对于GPS全球解坐标时间序列,轨道模型、对流层、海潮模型误差等为GPS中长基线解算的主要误差源,其噪声呈现出“闪烁噪声+白噪声”的特征[13, 14, 15, 16, 17, 18, 19, 20, 21]。短基线时间序列中消除了轨道模型误差以及对流层模型误差,仅有多路径效应、观测墩的稳定性等为GPS短基线解算的主要误差源,因此,短基线时间序列种所呈现出的噪声特征与长基线可能并不一致。GPS坐标时间序列中的噪声谱可以用指数定律来描述,其谱指数k为双对数空间种功率谱拟合直线的斜率。当-3<k<-1,为非平稳过程,也称为布朗运动。当-1<k<1为平稳过程为,也称为分形白噪声。其中,k=2时为随机漫步噪声;k=0时为白噪声;k=-1时为闪烁噪声。文献[13]利用双差算法计算1条50 m的基线12个星期的单历元(30 s)解坐标时间序列,利用FFT分析其功率谱,序列N、E、U分量的谱指数分别为-0.32,-0.35,-0.23。文献[10]年估计2.6 y的短基线时间序列中噪声的谱指数为N 1.4±0.2,E 1.5±0.2,U 0.9±0.3,由此可见,短基线时间序列由于处理方法(双差或单差)、测站位置不同,其噪声谱指数介于白噪声、闪烁噪声、随机游走噪声之间,目前仍未能建立最优的噪声模型,顾及了时间序列中的噪声特征,为了获得较为可靠的测站线性运动趋势以及周年信号,本文分别采用“白噪声(WH)”、“白噪声+闪烁噪声(WH+FN)”来模拟时间序列中的噪声。
| mm/a | ||||||
| 测站 | N | E | U | |||
| WH | WH+FN | WH | WH+FN | WH | WH+FN | |
| L022 | 0.0±0.03 | 0.4±0.20 | 1.9±0.02 | 2.2±0.19 | -3.8±0.04 | -3.9±0.28 |
| L132 | -0.0±0.04 | -0.0±0.36 | -0.8±0.03 | -0.7±0.15 | -1.4±0.05 | -1.4±0.19 |
| S071 | -0.5±0.05 | -0.8±0.37 | 2.0±0.12 | 2.3±0.62 | -0.8±0.06 | -0.9±0.41 |
| S171 | -0.0±0.05 | -0.2±0.37 | -0.3±0.04 | 0.1±0.17 | -0.5±0.07 | -0.3±0.19 |
| S191 | 0.0±0.04 | -0.0±0.25 | -0.2±0.03 | -0.0±0.27 | -1.0±0.06 | -0.9±0.21 |
| mm | ||||||
| 测站 | N | E | U | |||
| WH | WH+FN | WH | WH+FN | WH | WH+FN | |
| L022 | 0.7±0.02 | 0.6±0.11 | 0.8±0.02 | 0.7±0.11 | 0.9±0.02 | 0.8±0.11 |
| L132 | 0.6±0.03 | 0.5±0.18 | 0.4±0.02 | 0.3±0.07 | 0.4±0.02 | 0.4±0.18 |
| S071 | 0.5±0.04 | 0.8±0.21 | 1.1±0.09 | 1.2±0.60 | 0.2±0.04 | 0.3±0.21 |
| S171 | 0.2±0.04 | 0.2±0.23 | 0.9±0.04 | 0.8±0.10 | 0.6±0.04 | 0.6±0.13 |
| S191 | 0.5±0.03 | 0.5±0.13 | 1.0±0.02 | 1.0±0.14 | 0.2±0.03 | 0.2±0.13 |
采用2种噪声模型计算得到的线性速率以周年振幅如表 2、表 3所示,比较可知不同噪声模型下的速度及周年运动振幅的估值差异较小,但WN模型下估计得到的各参数精度要远高于WN+FN,研究表明,“WN+FN”模型下估计的速率方差要比WN模型大3~6倍[14]。根据极大似然估计原理,不同的噪声模型组合将得到不同的极大似然对数值(MLE),其数值越大,结果越可靠。比较本文中不同噪声模型计算得到的MLE值发现,采用WN计算结果优于WN+FN。可见本文中时间序列跨度较短(2 a),且间隔为4 h,其噪声仍以高频的白噪声为主,低频部分的闪烁噪声或随机游走噪声未能表现出来。
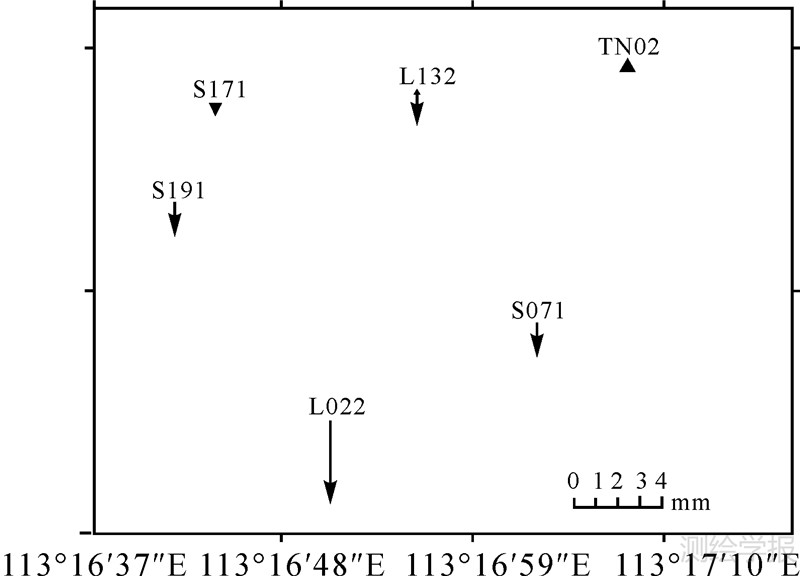
分析WN估计得到的线性速度,则西龙池GPS监测站的主要运动趋势为:L022运动速度为北偏东80°,2.2 mm/a;S071为北偏东109°,2.5 mm/a;L132为北偏西87°,0.7 mm/a。监测点S171、S191线性运动微弱,其速率小于0.3 mm/a,如图 5所示。各测站均存在不同程度的沉降,L022沉降速度最大,达3.7 mm/a。副坝上测点L132沉降速度为1.2 mm/a。其余测站S171、S191、S071分别为0.5 mm/a、1.0 mm/a、0.8 mm/a,如图 6所示。与其余断面相比,L022、S171所在的主坝以及L132所在的副坝体平面、垂直方向变形明显。

|
| 图 5 监测点水平方向运动速度 Fig. 5 Horizontal velocities of GPS stations in Xilongchi upper reservoir |
|
| 图 6 监测点垂直方向运动速度 Fig. 6 Vertical velocities of GPS stations in Xilongchi upper reservoir |
同时,不同的监测站N、E方向的周年振幅不一致。从表 3可以看出,L022 N、E方向上较为明显,振幅为~1 mm。S071、S171、S191测站则主要表现为E方向,振幅为~1 mm,L132主要表现为N方向上,振幅为0.5 mm。文献[6]模拟计算表明,基岩膨胀引起的GPS测站周年运动信号相对于温度存在1.5个月的滞后。文献[9]分析比对了测站短基线序列中的周年信号与气温数据后认为,周年信号与测区温度相关,其中深基坑[15]测站的周年信号相对于气温存在23~43 d的相位滞后,并且N、E分量呈现的周年信号存在~10 d的差异,根据所计算得到的周年运动滞后时间,认为短基线时间序列中周年信号可能主要是由于基岩的热膨胀导致,并且由于测站与基岩的相对位置关系,测站各方向的地质环境不同可能导致不同测站上各分量的周年运动振幅及相位存在差异。
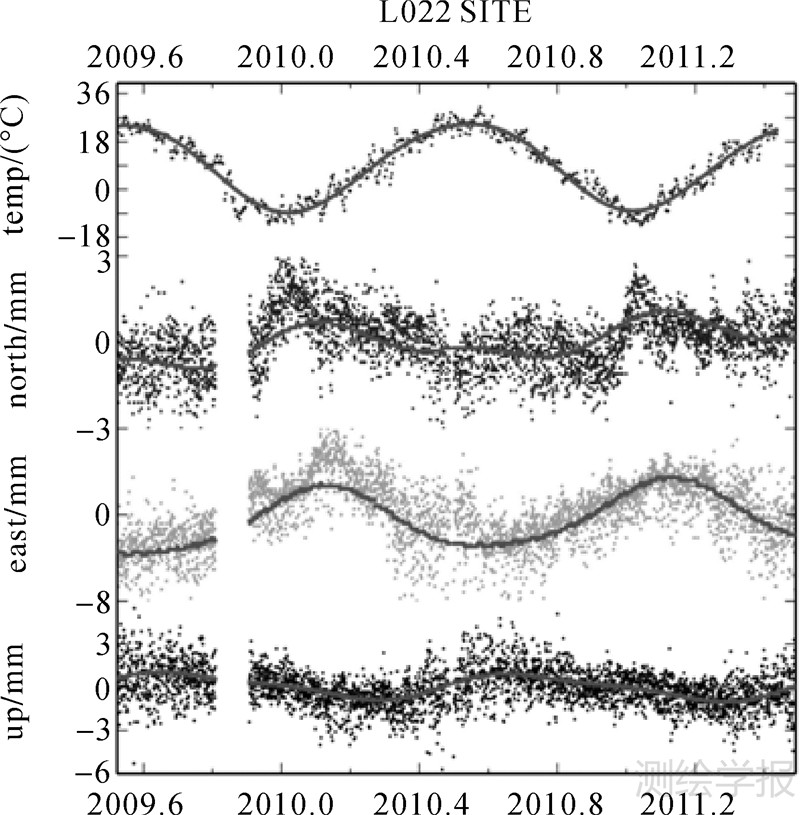
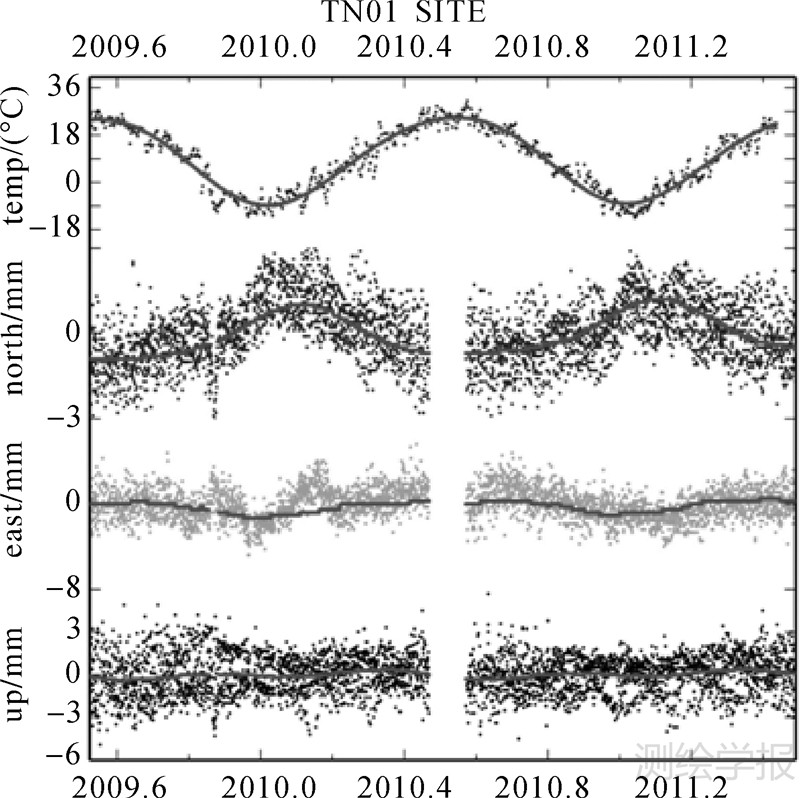
本文将时间序列中的线性趋势去除后,发现测站时间序列中的周年信号相对温度数据存在明显的滞后,滞后时间为L022 N分量(48±2) d,E分量(36±2) d,TN01 N分量(31±2) d,S071 E分量(8±44) d,S171 E分量(80±2) d,S191 E分量(71±2) d。由于各监测站的观测墩情况完全一致,忽略了观测墩的热膨胀,同时L022所处的主坝体结构坚固,且打入基岩上,TN01(基准站)、L022可视为深锚式天线墩[15],如图 7、图 8所示。笔者推测,L022、TN01测站时间序列中周年信号可能由其所处位置基岩的热膨胀导致,其余监测站的时间序列中某分量上的周年信号同样存在相对于温度的相位延迟,可能包括有基岩、地表热膨胀等导致的共同作用。
|
| 图 7 TN01测站坐标时间序列与测区温度的季节性变化 Fig. 7 Seasonal cycle for temperature and coordinate time series for all components for station L022 after removing of secular signal of a model,the red lines represents the same data fitted by the model |
|
| 图 8 TN01测站坐标时间序列与测区温度的季节性变化 Fig. 8 Seasonal cycle for temperature and coordinate time series for all components for reference station TN01 after removing of secular signal from a model,the red lines represent the same data fitted by the model |
本文利用西龙池上水库5个连续GPS监测点近2 y的观测数据,计算坐标时间序列,分析了该水库的长期变形趋势,包括以下几点结论:
(1) 噪声模型对线性速率及周年运动振幅估计的影响很小。对GPS短基线序列而言,本文2 y跨度的时间序列中噪声仍以高频的白噪声为主,低频部分的闪烁噪声或随机游走噪声并没有表现出来。
(2) 西龙池上水库已完成初次蓄水后整体上较为稳定,各监测点序列平面方向波动为-3~3 mm,高程方向波动-5~5 mm,同时,主副坝上的存在微弱的线性变形,其中L022运动速度为北偏东80°,2.2 mm/a,S071为北偏东109°,2.5 mm/a,L132为北偏西87°,大小为0.7 mm/a。监测点S171、S191线性运动微弱,其运动速度小于0.3 mm/a。各点均存在不同程度的沉降,L022沉降速度最大,达3.7 mm/a。副坝上测点L132沉降速度为1.2 mm/a。其余测站S171、S191、S071分别为0.5 mm/a,1.0 mm/a,0.8 mm/a。
(3) 监测站水平方向呈现出的周年运动信号并不一致,其中L022 N、E分量周年信号明显,振幅为~1 mm。S071、S171、S191测站则主要表现为E方向,振幅为~1 mm,L132主要表现为N方向上,振幅为~0.5 mm。L022、TN01测站的周年运动可能是由于基岩的热膨胀导致,其余测站的周年信号中包括有基岩以及地表热膨胀的共同作用。
利用连续的GPS观测资料确定了西龙池上水库的长期变形趋势,进一步的综合GPS监测结果与水库水文、气象等数据,建立相应的模型,有利于更好的揭示水库变形机理。
| [1] | KING M A, WILLIAMS S D P. Apparent Stability of GPS Monumentation from Short-baseline Time Series[J]. Jounal of Geophysical Research, 2009,114( B10):21-31. |
| [2] | WILLIAMS S D P. The Effect of Coloured Noise on the Uncertainties of Rates Estimated from Geodetic Time Series [J]. Journal of Geodesy, 2003, 76:483-494. |
| [3] | FARRELL W E. Deformation of the Earth by Surface Loads [J]. Reviews of Geophysics and Space Physics, 1972,10( 3):761-797. |
| [4] | JIANG Weiping, Er Dongchen, ZHAN Biwei,et al. New Model of Antarctic Plate Motion and Its Analysis[J]. Chinese Journal of. Geophysical Research, 2009, 52(1):41-49.(姜卫平,鄂栋臣,詹必伟,等.南极板块运动新模型的确定与分析[J].地球物理学报,2009,52(1):41-49.) |
| [5] | ZHU Wenyao, FU Yang, LI Yan. Global Height Vibration and Its Seasonal Variation Induced by GPS Height[J]. Science in China(Series D), 2003, 33(5):470-481. (朱文耀,符养,李彦. GPS高程导出的全球高程振荡运动及季节性变化[J].中国科学(D辑), 2003, 33(5):470-481.) |
| [6] | DONG Danan, FANG Peng, Bock Y,et al. Anatomy of Apparent Seasonal Variations from GPS-derived Site Position Time Series[J]. Jounal of Geophysical Research, 2002,107(B4): 2075- 2091. |
| [7] | FREYMUELLER J. Seasonal Position Variations and Regional Reference Frame Realization[C]//Proceedings of International Association of Geodesy Symposia. [S.l.]: Springer Verlag ,2009:191-196. |
| [8] | RAY J. Systematic Errors in GPS Position Estimates[R]. Darmstadt: IGS Workshop, 2006. |
| [9] | JIANG Weiping, ZOU Xuan, TANG Weiming. A New Kind of Real-Time PPP Method for GPS Single-Frequency Receiver Using CORS Network[J]. Chinese Journal of Geophysical Research,2012,55 (5):1549-1556.(姜卫平,邹璇,唐卫明.基于CORS网络的单频GPS实时精密单点定位新方法[J].地球物理学报,2012,55 (5):1549-1556.) |
| [10] | HILL E M, DAVIS J L, PEDRO Elo’segui,et al. Characterization of Site-Specific GPS Error Using a Short-Basline Network of Braced Monuments at Yucca Mountain, Southern Nevada [J]. Journal of Geophysical Research,2009,114(B11402):1-13. |
| [11] | KING M A, WATSON C S. Long GPS Coordinate Time Series: Multipath and Geometry Effects[J]. Journal of Geophysical Research, 2010, 115(B04403):7495-7518. |
| [12] | WILLIAMS S D P. CATS: GPS Coordinate Time Series Analysis Software [J]. GPS Solution, 2008, 12:147-153. |
| [13] | NIKOLAIDIS R. Observation of Geodetic and Seismic Deformation with the Global Positioning System[D]. San Diego:Unversity of California, 2002. |
| [14] | MEISEL B, ANGERMANN D, KRUGEL M. Influence of Time Variable Effects in Station Positions on the Terrestrial Reference Frame[C]//Proceedings of International Association of Geodesy Symposia. Berlin:[s.n.],2009. |
| [15] | TIAN Yunfeng, SHEN Zhengkang. Progress on Reduction of Non-tectonic Noise in GPS Position Time Series[J]. Acta Seismologica Sinica,2009,31(1):68-81.(田云锋,沈止康. GPS坐标时间序列中非构造噪声的剔除方法研究进展[J].地震学报,2009,31(1):68-81.) |
| [16] | JIANG Zhihao, ZHANG Peng, BI Jinzhong, et al. The Model of Crustal Horizontal Movement Based on CGCS2000 Frame [J]. Acta Geodaetica et Cartographica Sinica, 2009,38(6): 471-476. (蒋志浩,张鹏,秘金钟,等.基于CGCS2000的中国地壳水平运动速度场模型研究[J].测绘学报,2009,38(6): 471-476.) |
| [17] | JIANG Zhihao,ZHANG Peng, BI Jinzhong, et al. Velocity Estimation on the Colored Noise Properties of CORS Network in China Based on the CGCS2000 Frame[J].Acta Geodaetica et Cartographica Sinica, 2010,39(4):355-363.(蒋志浩,张鹏,秘金钟,等.顾及有色噪声影响的CGCS2000下我国CORS站速度估计[J].测绘学报,2010,39(4):355-363.) |
| [18] | YUAN Linguo, DING Xiaoli, CHEN Wu,et al. Characteristics of Daily Position Time Series from Hong Kong GPS Fiducial Network[J]. Chinese Journal of Geophysics, 2008,51(5):1372-1384. (袁林果,丁晓利,陈武,等.香港GPS基准站坐标序列特征分析[J].地球物理学报,2008,51 (5): 1372-1384.) |
| [19] | QIAO Xuejun, WANG Qi, WU Yun,et al. Time Series Characteristic of GPS Fiducial Stations in China[J]. Geomatics and Information Science of Wuhan University, 2003, 28(4) :413 -416. (乔学军,王琪,吴云,等.中国大陆GPS基准站的时间序列特征[J].武汉大学学报:信息科学版,2003,28(4):413-416.) |
| [20] | WANG Min, SHEN Zhengkang, DONG Danan. Effects of Non-tectonic Crustal Deformation on Continuous GPS Position Time Series and Correction to Them[J]. Chinese Journal of. Geophysical Research, 2005,48(5):1045-1052. (王敏,沈正康,董大南.非构造形变对GPS连续站位置时间序列的影响和修正[J].地球物理学报,2005,48(5):1045-1052.) |
| [21] | HUANG Liren. Noise Properties in Time Series of Coordinate Component at GPS Fiducial Stations[J]. Journal of Geodesy and Geomatics, 2006, 26(2):31-38. (黄立人. GPS基准站坐标分量时间序列的噪声特性分析[J].大地测量与地球动力学, 2006, 26(2):31-38.) |
| [22] | LANGBEIN J. Noise in GPS Displacement Measurements from Southern California and Southern Nevada [J].Journal of Geophysical Research, 2008,113(B05405):5247-5259. |


