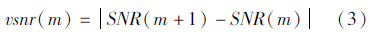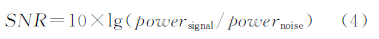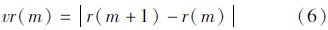1 引 言
数据去噪是大地测量数据处理的一项首要工作,直接影响后续数据处理结果的可靠性。近年来,小波分析以其良好的时频局部化、多分辨率分析及处理非线性问题的能力,已经在大地测量数据去噪方面得到了广泛应用[1, 2, 3, 4]。小波去噪时,信号的分解与重构尺度对去噪结果具有很大影响。分解与重构的尺度过小时,数据中将仍存在较多噪声数据;尺度过大时,则会把部分细节信息当作噪声剔除。因此,合理确定小波分解与重构的最佳尺度对于提高小波去噪的可靠性与有效性具有重要的价值,也是当前小波去噪研究中的一个难点问题。
现有小波去噪分解尺度的定量选择方法主要可以分为两类:①基于信号特征的方法[4, 5, 6, 7, 8, 9, 10];②基于噪声特征的方法[11, 12, 13, 14, 15, 16]。现有基于信号特征的方法主要根据去噪信号的均方根误差、熵、相关性等的变化规律指导最佳分解尺度选择。文献[4, 5]提出当去噪后信号均方根误差变化较小时分解尺度为最佳;文献[6]依据小波基与信号长度的变化特征确定最佳的分解尺度;文献[7, 8]根据小波系数熵和小波变换功率谱的变化特征进行最佳分解尺度的选择;文献[9]采用小波重构信号与原始信号的相关性来确定最佳分解尺度;文献[10]将均方根误差、相关系数、信噪比及光滑度归一化后求和,利用极值来确定最佳分解尺度。现有基于噪声特征的方法首先假设信号中的噪声为白噪声,然后通过建立假设检验条件进行判定,超过条件即停止分解。文献[11, 12]分别发展了采用卡方白化检验与K-S白化检验对小波分解的高频系数进行检验。文献[13]首先对小波分解高频系数进行奇异谱分解来确定最佳分解尺度。文献[14, 15, 16]发展了类似的小波去相关白化检验方法。
然而实际应用中,现有的小波分解尺度选择方法存在一定局限:①现有基于信号特征的方法中,单一指标的变化规律经常不够准确,无法进行判断;②现有基于噪声特征的方法,需要借助白噪声假设条件,若噪声不满足这一假设,其判断准确性则难以保证。而且,此类方法均需要数据满足经典统计学理论的大样本条件,而小波分解过程中高频系数的个数以指数降低,难以满足概率分布假设。因此,发展更为准确、更具普适性的小波去噪最佳分解尺度选择方法需要引起充分的重视。为此,本文试图从信号本身的特征的出发,发展一种新的小波分解尺度选择方法。其主要研究思路在于提取信号去噪过程中的多方面变化规律,进而将多类特征进行融合,从更全面的角度描述信号随小波分解尺度变化而表现出的客观规律。最终,通过识别信号定量变化特征与小波分解尺度的对应关系,进行小波去噪最佳分解尺度的选择。下面,具体介绍本文发展的多指标融合的小波去噪分解尺度选择方法。
2 多指标融合的小波去噪最佳分解尺度选择要将多个小波去噪最佳分解尺度选择的指标融合,涉及3个核心问题:选择哪些指标、如何融合、如何识别最佳分解尺度。下面分别对这3个问题的解决进行具体阐述。
2.1 融合指标的选择融合指标选择的关键在于确定能够从不同角度描述去噪信号特征的定量表达方法。现有对小波去噪信号的描述指标主要包括均方根误差,信噪比,互相关系数以及平滑度等[4, 5, 6, 7, 8, 9, 10]。均方根误差指分解与重构信号与原始信号的均方根误差,其值越小表示去噪效果越好。信噪比指原始信号能量与噪声能量的比值,一般认为,信噪比越高,滤波效果越好。平滑度指标指去噪后信号的差分数的方差根与原始信号的差分数的方差根之比,信号越光滑,平滑度指标的数值越小,去噪效果越好。互相关系数指小波去噪后的信号与理论参考信号的相似度,其值越接近1,去噪信号与原信号的拟合程度越好。据此可知:①均方根误差实际上体现了信号的整体偏差信息;②信噪比体现了噪声信息对整体信号的影响;③平滑度体现了信号的局部变异信息,即是否有较多的局部突变;④互相关系数体现了去噪信号与理论参考信号的拟合信息。由于实际中理论参考信号未知,互相关系数计算的准确性不高,且互相关系数与均方根误差均为信号整体偏差信息的度量,具有很大的重叠性,故本文中选择均方根、信噪比及平滑度3个指标来构造融合指标。由于实际信号是未知的,故无法直接通过与真实信号的比较来描述去噪信号的特征。为此,借助变化率特征[4, 5, 7,8, 10]来重新构造了3个描述指标:均方根误差变化量vrm)、信噪比变化量(vsnr)以及平滑度变化量(vr),具体表达如下
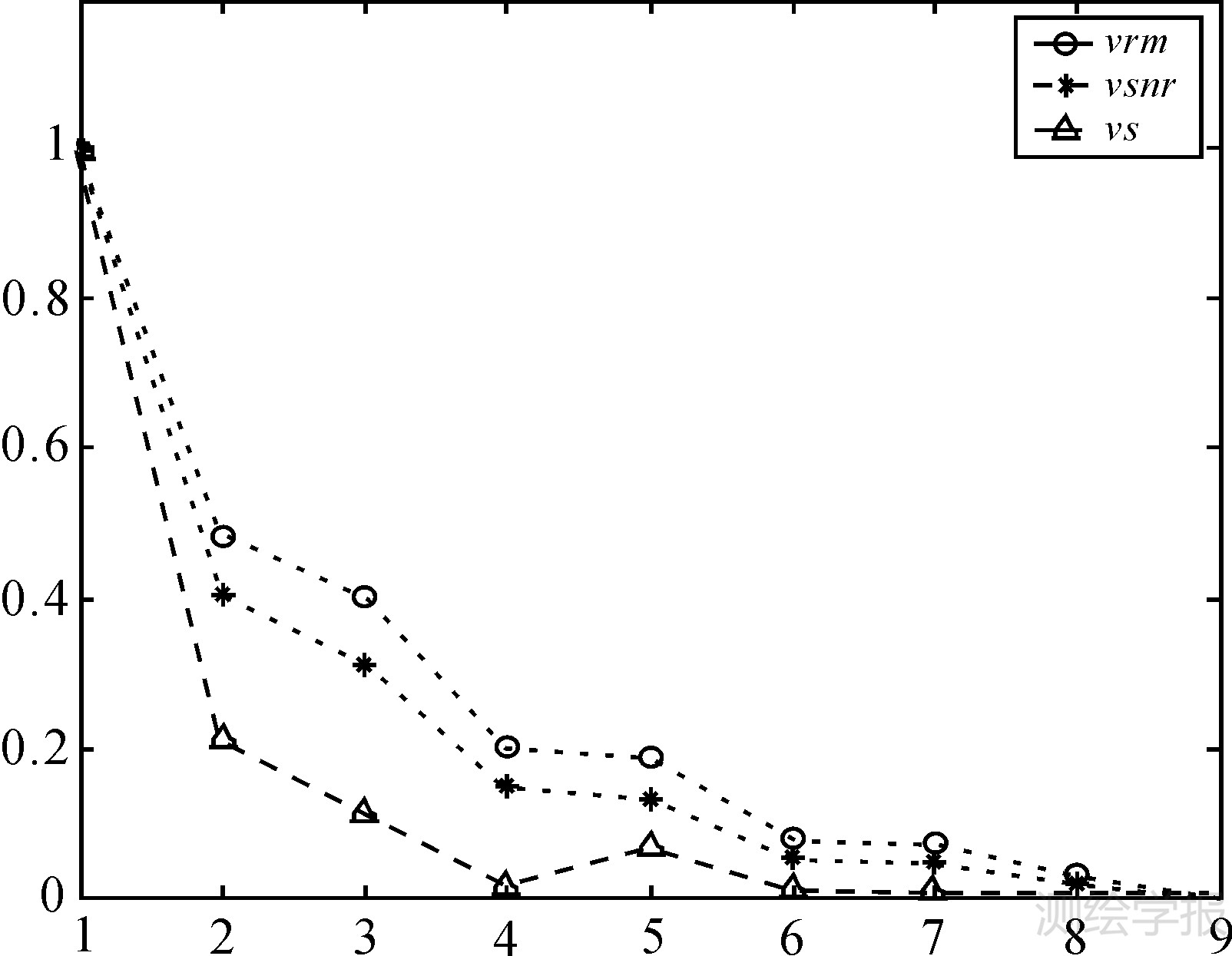
式中,vrm(m)表示尺度m+1与尺度m间的均方根误差变化量;RMSE(m)表示第m分解尺度下的均方根误差,表达为 式中,f(i)表示原始信号;fm(i)表示m尺度下的分解重构信号;n表示信号长度。 式中,vsnr (m)表示尺度m+1与尺度m间信噪比变化量;SNR (m)表示第m分解尺度下的信噪比,表达为 式中,vr(m)表示尺度m+1与尺度m间的平滑度变化量;r(m)表示第m分解尺度下的平滑度,表达为实际中,均方根误差变化量、信噪比变化量以及平滑度变化量伴随着分解尺度的增加均表现出明显的收敛特性,如图 1所示,信噪比为2的Blocks标准信号采用haar小波基进行多层次分解去噪后,均方根误差变化量、信噪比变化量以及平滑度变化量归一化后的变化趋势(横轴表示分解尺度),可见分解尺度大于4或5后,指标值均趋于平缓。本文借助这一特性进一步构造融合的评价指标进行小波分解尺度选择。
|
| 图 1 均方根误差变化量、信噪比变化量以及平滑度变化量 Fig. 1 Variations of vrm,vsnr and vs |
由图 1可见,均方根误差变化量、信噪比变化量以及平滑度变化量随去噪尺度的增加,其变化存在一定的趋势。为了更全面反映信号的变化特征,本文对多指标进行融合。在信息论中,熵是对于信息不确定性的一种度量。信息的量越大,其不确定性就越小,熵也就越小;反之,信息量越小,不确定性越大,而熵也越大。根据熵的该特性,可以用熵值法对各指标进行加权融合,通过计算熵值来判断某个指标的离散程度,若某项指标值变异程度越大,指标的离散程度越大,该指标对于综合评价的影响越大,则该指标的权重越大;反之亦然。具体表达为
式中,F(m)为加权融合指标;wvrm、wvsnr、wvs分别表示由熵值计算得到的均方根误差变化量、信噪比变化量以及平滑度变化量所占权重;m表示小波分解的尺度;Cvrm、Csnr、Cvs分别表示均方根误差变化量、信噪比变化量以及平滑度变化量的归一化结果,表达为进一步,以归一化均方根误差变化量(Cvrm)为例给出指标权重的计算方法
式中,H表示指标熵值;N表示序列长度;P表示概率。信噪比变化量以及平滑度变化量的熵值计算方法与式(13)和式(14)相同。 2.3 最佳分解尺度识别现有研究[4, 5]以及本文试验发现,信号去噪过程中,某些指标(如均方根误差)存在收敛特性,即达到最佳分解尺度后,变化率显著降低并趋于平稳。这种特性与聚类分析有效性评价中经典的Hubert's Г指数[17]具有类似的特征,可以通过识别指标变化的拐点来识别最佳分解尺度。本文借鉴Hubert's Г指数采用的拐点法来识别小波去噪的最佳分解尺度。依据2.2节中融合指标的计算方法,首先对信号进行多个尺度的分解(一般分解为8~10个尺度),获得融合指标序列。图 2(a)中展示了图 1中3个变量加权融合后的结果,可以发现其变化曲线具有明显的收敛趋势。为得到更易于观察曲线的收敛趋势,同时与通常的分析习惯吻合,将原始数据分别减去最大值进行反转,如图 2(b)所示。

|
| 图 2 最佳分解尺度选择 Fig. 2 Identify the best decomposition scale |
针对反转处理后的序列,进一步进行以下两步操作:①异常值剔除,实际中可能出现个别的异常值偏离整体的变化趋势,本文首先采取最小二乘拟合对序列的整体变化趋势进行判断,拟合阶数取为4[17],进一步,采取小样本异常值判别的中位数绝对偏差法[18],剔除可能存在的异常值,并用相应的拟合值代替。如图 2(b)中所示,实线为拟合曲线,通过判别发现没有异常值;②拐点识别,将经过异常值处理后的序列连接,如图 2(c)所示。第4个值对应比较明显的拐点,故可以认为最大分解尺度为5。通过计算原始理论参考信号与去噪后信号的均方根误差发现,分解尺度为5时去噪效果最佳,因此,通过拐点识别的结果与实际情况是吻合的。进一步,将采用4组试验来说明本文提出方法的有效性与优越性。 3 试验分析与比较 3.1 试验设计
设计试验数据时首先需要考虑两方面因素:①为了能够准确地获得小波去噪质量的实际评价效果,需要选取真值已知的数据进行分析,即原始理论参考信号已知;②为了全面反映小波去噪质量评价方法的应用效果,需要充分顾及实际去噪数据的固有特性。通过总结分析已有研究[2, 3, 4, 10],可以发现去噪数据主要存在3个方面主要差异:①平滑度差异,即真实数据中是否存在较多的突变;②真实数据可能存在平稳和非平稳两种情况;③不同信噪比(高或低)的去噪信号。针对去噪信号的以上3方面差异,本文针对性的选择两组数据:Blocks标准信号(如图 3(a)所示,N=1024)和一组模拟的变形监测数据S(图 3(d)所示,N=1024),其中模拟数据为采用3个不同频率的正弦信号以及一个低频趋势信号叠加产生的变形监测数据
式中B1(如图 3(b)所示)和S1(如图 3(e)所示)为加入信噪比为2的白噪声的含噪信号,B2((如图 3(c)所示))和S2((如图 3(d)所示))为加入信噪比为10的白噪声的含噪信号。本文设计的4组含噪信号可以充分顾及实际含噪信号的固有特点且真值已知,对去噪结果具有准确的先验知识。由于原始理论参考信号已知,即已知未加噪声的纯净信号,所以可求得重构信号与原始纯净信号的均方根误差值(区别于评价标准中的RMSE),当该均方根误差最小时,视为最佳的去噪结果。为了进行比较分析,本文选取了基于均方根误差变化的方法[4, 5]、综合法[10]、小波高频系数白化检验法[11]以及小波去相关白化检验法[14]等已有的4种方法进行试验对比。试验分析时,选取3种常用的小波基haar、db8和sym6,进行10个层次的分解与重构。

|
| 图 3 试验数据 Fig. 3 Experimental data |
通过对信号B1计算重构信号与原始纯净信号的均方根误差后发现:采用haar小波基在第5层上的去噪效果最好。信号B1进行加权融合判别的具体方法与结果已列于图 1和图 2。进一步给出4种比较方法的判别结果,如图 4所示。依据文献[4]中方法,均方根误差变化率小于1.1时,即为最佳分解尺度;综合法为最大值时为最佳分解尺度。分析图 4中对比试验结果可以发现:①均方根误差变化率与综合法均给出了错误的识别结果,而且过去噪时均方根误差法反而认为其效果更好;②高频系数检验法以及小波去相关白化检验法均没有出现拒绝假设的情况,其根本原因在于样本数量过小,导致假设检验方法不能使用。

|
| 图 4 B1信号对比试验结果 Fig. 4 Experimental results of B1 |
对于信号B2,通过计算重构信号与原始纯净信号的均方根误差后发现,采用haar小波基在第3或4层上的去噪效果最佳。如图 5所示,本文方法识别的结果为第3尺度的效果最佳,与实际相吻合。图 6中展示了4种对比方法对B2信号的试验结果,同样可以发现没有一种方法可以正确的识别最佳的分解尺度。

|
| 图 5 B2信号多指标融合试验结果 Fig. 5 Experimental results by the hybrid indicator B2 |
对于S1信号为例,通过计算重构信号与原始纯净信号的均方根误差后发现,采用db8小波基在第4层上的去噪效果最好。图 7中所示的多指标融合方法的判别结果很好地与实际情况吻合,而图 8中对比方法有的给出了错误的结论,如均方根误差变化率和综合法;有的无法进行判断,如高频系数白化检验和小波去相关白化检验。

|
| 图 6 B2信号对比试验结果 Fig. 6 Experimental results of B2 |

|
| 图 7 S1信号多指标融合试验结果 Fig. 7 Experimental results by the hybrid indicator S1 |

|
| 图 8 S1信号对比试验结果 Fig. 8 Experimental results of S1 |

|
| 图 9 S2信号多指标融合试验结果 Fig. 9 Experimental results by the hybrid indicator S2 |

|
| 图 10 S2信号对比试验结果 Fig. 10 Experimental results of S2 |
提出一种多指标融合的小波去噪最佳分解尺度选择方法。通过融合去噪过程中信号均方根误差、信噪比及光滑度变化量构造了随小波分解尺度变化具有收敛特性的新统计量。最后,通过识别变化拐点的方法来识别小波去噪的最佳分解尺度。通过多组代表性数据的实际分析与比较发现:①该方法可以有效地识别去噪的最佳尺度,且计算较为简便;②与现有方法相比,该方法的准确性更好。进一步,将该方法在大地测量数据处理中进行实际应用,以进一步验证其实用性。
| [1] | NING Jinsheng,WANG Haihong,LUO Zhicai.Applications of Wavelet Analysis in Geodesy and Its Progress[J].Geomatics and Information Science of Wuhan University,2004,29(8):659-663.(宁津生,汪海洪,罗志才.小波分析在大地测量中的应用及其进展[J].武汉大学学报:信息科学版,2004,29(8):659-663.) |
| [2] | HUANG Shengxiang,LIU Jingnan.A Novel Method for Reducing Noises in GPS Deformation Monitoring System[J].Acta Geodaetica et Cartographica Sinica,2002,31(2):104-107.(黄声享,刘经南.GPS变形监测系统中消除噪声的一种有效方法[J].测绘学报,2002,31(2):104-107.) |
| [3] | WU Fumei,YANG Yuanxi.Integrated Navigation by Adaptive Filtering Based on Wavelet Threshold De-noising[J].Acta Geodaetica et Cartographica Sinica,2007,36(2):124-128.(吴富梅,杨元喜.基于小波阈值消噪自适应滤波的GPS/INS组合导航[J].测绘学报,2007,36(2):124-128.) |
| [4] | WEN Hongyan.Research on Deformation Analysis Model Based on Wavelet Transform Theory[D].Wuhan:Wuhan University,2004.(文鸿雁.基于小波理论的变形分析模型研究[D].武汉:武汉大学,2004.) |
| [5] | DONOHO D L,JOHNSTONE L.Ideal Spatial Adaptation by Wavelet Shrinkage[J].Biometrika,1994,81(3):425-455. |
| [6] | PU R,GONG P.Wavelet Transform Applied to EO-1 Hyperspectral Data for Forest LAI and Crown Dosure Mapping[J].Remote Sensing of Environment,2004,91(2):212-224. |
| [7] | SUN W,MUKHERJEE R,STROEVE P,et al.A Multi-resolution Approach for Line-edge Roughness Detection[J].Microelectronic Engineering,2009,86(3):340-351. |
| [8] | XU K,WANG X,LI Y.Fundamental Wave Extraction and Frequency Measurement Based on IIR Wavelet Filter Banks[J].Measurement,2007,40(6):665-671. |
| [9] | KAEWPIJIT S,MOIGNE J L,EIGHAZAWI T.Automatic Reduction of Hyperspectral Imagery Using Wavelet Spectral Analysis[J].IEEE Transactions on Geoscience and Remote Sensing,2003,41(4):863-871. |
| [10] | LI Zongchun,DENG Yong,ZHANG Guanyu,et al.Deformation Measurement of Abnormal Data in the Wavelet Transform to Determine the Best Series[J].Geomatics and Information Science of Wuhan University,2011,36(3):285-288.(李宗春,邓勇,张冠宇,等.变形测量异常数据处理中小波变换最佳级数的确定[J] .武汉大学学报:信息科学版,2011,36(3):285-288.) |
| [11] | ZHANG Jixian,ZHONG Qiuhai,DAI Yaping.The Determination of the Threshold and the Decomposition Order in Threshold De-noising Method Based on Wavelet Transform[J].Proceedings of the CSEE,2004,24(2):118-122.(张吉先,钟秋海,戴亚平.小波门限消噪法应用中分解层数及阈值的确定[J].中国电机工程学报,2004,24(2):118-122.) |
| [12] | DU Wenliao,ZHU Rumin,LI Yanming.Adaptive Selection of Optimal Decomposition Level in Filtering Algorithm Based on Wavelet Transform[J].Journal of Optoelectronics·Laser,2010,21(9):1408-1411.(杜文辽,朱茹敏,李彦明.小波滤波分解层数的自适应确定方法[J].光电子·激光,2010,21(9):1408-1411.) |
| [13] | CAI Tie,ZHU Jie.Adaptive Selection of Optimal Decomposition Level in Threshold De-noising Algorithm Based on Wavelet[J].Control and Decision,2006,21(2):217-220.(蔡铁,朱杰.小波阈值降噪算法中最优分解层数的自适应选择[J].控制与决策,2006,21(2):217-220.) |
| [14] | WANG Wei,ZHANG Yingtang,REN Guoquan.Adaptive Selection and Simulation of Optimal Decomposition Level in Threshold De-noising Algorithm Based on Wavelet Transform[J].Chinese Journal of Scientific Instrument,2009,30(3):526-530.(王维,张英堂,任国全.小波阈值降噪算法中最优分解层数的自适应确定及仿真[J].仪器仪表学报,2009,30(3):526-530.) |
| [15] | LI Wei,CHEN Xiaohui,MAO Haijie.A Study of Adaptive Optimal Decomposition Level in Threshold De-noising Algorithm Based on Wavelet Transform[J].Computer Simulation,2009,26(3):311-313.(李炜,陈晓辉,毛海杰.小波阈值消噪算法中自适应确定分解层数研究[J].计算机仿真,2009,26(3):311-313.) |
| [16] | LIU Bin,DAI Guiping.Adaptive Wavelet Thresholding Denoising Algorithm Based on White Noise Detection and 3σ Rule[J].Journal of Transduction Technology,2005,18(3):473-476.(刘彬,戴桂平.基于白化检验和3σ准则的小波阈值去噪算法[J].传感器学报,2005,18(3):473-476.) |
| [17] | HALKIDI M,BATISTAKIS Y,VAZIRGIANNIS M.On Clustering Validation Techniques[J].Journal of Intelligent Information Systems,2001,17(2-3):107-145. |
| [18] | YUAN Jie,SHI Haibo,LIU Chang.Construction of Fuzzy Membership Functions Based on Least Squares Fitting[J].Control and Decision,2008,23(11):1263-1266.(袁杰,史海波,刘昶.基于最小二乘拟合的模糊隶属函数构建方法[J].控制与决策,2008,23(11):1263-1266.) |
| [19] | LIU Qiliang,DENG Min,WANG Jiamu,et al.Spatio-Temporal Outliers Detection within the Space-time Framework[J].Journal of Remote Sensing,2011,15(3):457-474.(刘启亮,邓敏,王佳璆,等.时空一体化框架下的时空异常探测[J].遥感学报,2011,15(3):457-474.) |
| [20] | TAO Ke,ZHU Jianjun.A Comparative Study of Validity Assessment of Wavelet De-noising[J].Journal of Geodesy and Geodynamics,2012,32(2):128-133.(陶珂,朱建军.小波去噪质量评价方法的对比分析研究[J].大地测量与地球动力学,2012,32(2):128-133.) |