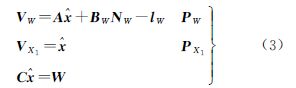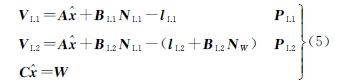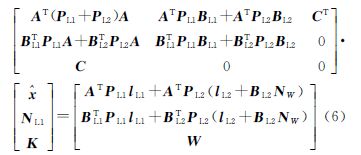2. 河北工业大学 土木学院 测绘工程系，天津 300401；
3. 河北省土木工程技术研究中心，天津 300401
2. Department of Surveying Engineering,Hebei University of Technology,Tianjin 300401,China；
3. Civil Engineering Technology Research Center of Hebei Province,Tianjin 300401,China
1 引 言
GPS动态定位时，周跳探测是一个比较棘手而又易出错的环节，解决该问题的一个途径是单历元定位。单历元定位仅根据当前一个历元的数据实现定位，无需考虑周跳问题[1]。单历元动态定位时，为了获得可靠的模糊度真值，需要附加较强的约束或先验条件。文献[2, 3, 4, 5, 6, 7]将单历元算法用于建筑物变形监测中；在姿态定位中单历元算法也有着广泛应用[8, 9, 10, 11, 12]；文献[13, 14]通过运动过程中的运动轨迹约束或基线长度约束，实现单历元动态定位；文献[15]通过两步搜索法实现单历元定位。约束条件的使用有两种方式[13]：一种是将此约束条件与双差观测方程一起解算，达到改善模糊度浮点解的效果，其后用LAMBDA方法可以更快地固定模糊度；另外一种是先不考虑约束条件，将伪距和相位一起形成双差方程，按常规方法解算整周模糊度，再进行约束检验，如果不满足条件，则选用残差平方和次小的一组解为最优解，再进行约束检验，直到满足条件为止。
本文针对列车沿固定线路运行的特点，提出附加轨迹约束的宽巷模糊度分解算法。当GPS接收机沿线路中线运动时，其运动轨迹分别受平面线型和竖向两方面的约束，加入此约束条件后有望提高模糊度分解的成功率。约束条件可根据接收机当前里程和线路模型来构成。通过伪距差分的概略位置，判断接收机所处的大致里程，调出该里程处的线路平面线形和竖向线形设计数据，形成三维空间直线约束条件。在只有平面设计数据时，形成空间平面约束条件，然后按照第一种约束条件的使用方法首先进行宽巷模糊度固定，宽巷模糊度成功固定后，利用宽巷模糊度和约束条件，分别固定L1、L2模糊度，最终实现单历元定位。
2 线路约束条件下的模糊度解算数学模型 2.1 线路计算模型 2.1.1 由里程计算中桩坐标及高程
铁路中线平面由直线、圆曲线和缓和曲线组成，称这三种线形为曲线元，直线曲率半径为无穷大，缓和曲线曲率半径在无穷大与圆曲线半径之间变化。曲线元上某一点的坐标，可由该曲线元的起点里程、终点里程、起点曲率半径、终点曲率半径、起点切线方位角、起点坐标、曲线的偏向计算得到[16]。
线路竖向为坡度线和连接相邻坡度线的圆曲线组成。任意一点的高程可以里程为索引，根据变坡点高程、坡度值、圆曲线半径计算得到。
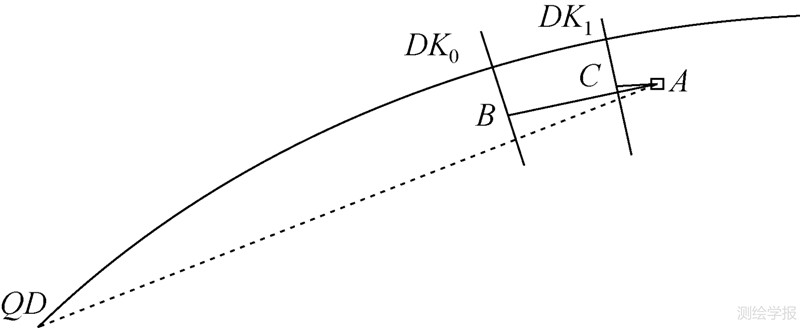
如图 1所示，设A为线路中线附近的一点；QD为线路起点；QD的里程为DKQD，A点到QD点的水平距离为DQD-A，则A点的近似里程为DK0=DKQD+DQD-A。设过DK0的法线为DK0－B，A到该法线的距离为DA-B，则A点里程的进一步趋近值为DK1=DK0+DA-B。重复前面步骤，直至A至某一里程处的法线距离小于某一阈值为止(可取为0.1mm)。
|
| 图 1 由坐标计算里程 Fig. 1 Calculating the mileage using the coordinates |
线路坐标系下的坐标一般为在测区中央子午线及平均高程面下的高斯平面坐标，约束条件的建立涉及与WGS-84坐标相互转换的问题。坐标转换有平面转换模型和空间转换模型两种方式。平面转换模型适合测区范围较小的地方，空间转换模型适用于大范围GPS测量。考虑到线路为很长的线状工程，本文采用空间转换七参数模型，可通过3个公共点得到转换七参数。需要说明的是在计算七参数时可以用正常高来替代大地高[17]。
由于曲线约束条件的建立较为复杂，本文用直线约束条件近似代替曲线约束条件。因为当平面圆曲线半径为2000m，竖向圆曲线半径为5000m时，用2m长的直线段来替代曲线，两者最大偏差不超过1mm，因此用较短的直线段来替代曲线不光形式简单，精度也是可以保证的。
当接收机沿铁路中线运动时，如图 2所示。设R为伪距差分定位的点位，其在WGS-84坐标系下的坐标为(XR,YR,ZR)WGS-84，其点位精度在1m左右。设其在线路中线上精确位置为T点，则线路约束方程可按以下步骤建立：
|
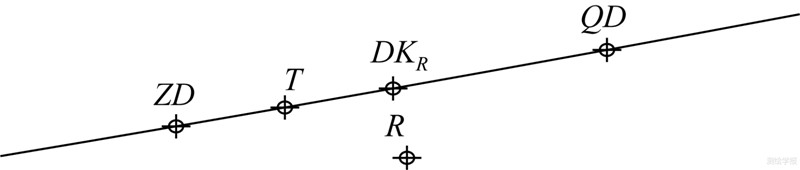
| 图 2 空间直线约束条件的建立 Fig. 2 Establishment of spatial linear constraint |
(1)(XR,YR,ZR)WGS-84经七参数转换得到线路坐标系对应椭球下的空间直角坐标(XR,YR,ZR)road。
(2)由(XR,YR,ZR)road计算大地坐标(BR,LR,HR)road。
(3)将(BR,LR)road经高斯投影得到高斯平面直角坐标(xR,yR)road。
(4)由(xR,yR)road计算出其对应的中桩里程DKR，具体计算公式参见文献[16]。将DKR分别加减1m得到两个新的里程，其对应的点分别为QD、ZD，根据这两个里程及线路设计数据计算出其在线路坐标系下的坐标分别为(xQD,yQD,HQD)、(xZD,yZD,HZD)。
(5)将(xQD,yQD,HQD)、(xZD,yZD,HZD)按高斯投影反算转换为大地坐标(BQD,LQD,HQD)road、(BZD,LZD,HZD)road。
(6)将(BQD,LQD,HQD)road、(BZD,LZD,HZD)road转换为空间直角坐标(XQD,YQD,ZQD)road、(XZD,YZD,ZZD)road。
(7)根据7个转换参数将(XQD,YQD,ZQD)road、(XZD,YZD,ZZD)road转换为WGS-84坐标系下的三维空间直角坐标：(XQD,YQD,ZQD)WGS-84、(XZD,YZD,ZZD)WGS-84，对应的直线方程为
式中
代入X的近似坐标后得
在只考虑线路平面线形的情况下，可建立二维平面约束。此时可将QD、ZD两点的大地高取为(HR)road+0.1m，重新计算其三维空间直角坐标，这样QD、ZD、DKR 3点不在一条直线上，可以得到唯一的空间约束平面。
2.3 轨迹约束下的宽巷模糊度解算
仅根据一个历元的相位观测数据，法方程秩亏数为3，无法解算未知数。将伪距差分平差后的未知数平差值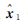
作为一组权为PX1的虚拟观测值，并用VX1表示其改正数，与2.2或2.3节中的约束条件、宽巷双差相位观测方程一起构成如下数学模型
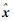NW分别为坐标改正数和宽巷模糊度向量；A、BW为其对应的系数阵；lW为双差观测值与计算值的差值；PW为宽巷双差观测值的权阵；PX1由伪距差分得到。应用最小二乘准则，得法方程
通过上述法方程解算宽巷模糊度的浮点解，并提取其方差-协方差阵，用LAMBDA方法固定宽巷模糊度。由于附加约束后，模糊度的浮点解及其方差阵得到改善，有利于提高模糊度分解的成功率。
2.4 轨迹约束下的L1、L2模糊度解算在宽巷模糊度固定后，在列L1、L2观测值的误差方程时，根据NW=NL1-NL2，将误差方程表达为只含有L1模糊度NL1的形式。结合约束条件，得到如下数学模型
式中，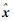
为坐标改正数；NL1、NW分别为L1、LW模糊度向量；A为坐标改正数系数阵；BL1、BL2为L1双差模糊度、L2双差模糊度对应的系数阵；lL1、lL2分别为L1、L2双差观测值与计算值的差值；PL1、PL2分别为L1、L2双差观测值的权阵。其法方程为
用LAMBDA方法将L1模糊度固定后，回代到误差方程中，重新组成法方程，得到最终坐标。
3 算例分析试验在河北工业大学新校区进行，接收机为合众思壮E660，基站安置在土木学院楼门前，流动站被安置在汽车上沿学校内部主干道以40km/h运行，采样间隔为0.2s。为了检验宽巷组合和轨迹约束对模糊度固定的有效性，选取一段比较平顺的轨迹进行解算，共315个历元。为突出显示轨迹的变化，图 3中将基站的x坐标向北平移了500m，基线长度在566.477~677.813m之间。利用LGO解算软件，在中央子午线117°03′01″，投影高程面1.3m的设置下，得到高斯平面坐标系下的坐标，用直线和圆曲线以及平面分别来拟合这段轨迹，构造约束条件。分别按照以下6种方案解算：
|
| 图 3 汽车运行轨迹 Fig. 3 The car’s track |
方案1：直接采用L1、L2双差观测数据按照阻尼LAMBDA方法解算。
方案2：L1、L2双差观测数据结合平面约束的方法解算模糊度。
方案3：L1、L2双差观测数据结合空间直线约束的方法解算模糊度。
方案4：先宽巷组合按照阻尼LAMBDA方法解算，再固定L1、L2模糊度解算。
方案5：先宽巷组合结合平面约束的方法固定宽巷模糊度；L1、L2双差观测数据结合平面约束固定L1、L2双差模糊度。
方案6：先宽巷组合结合空间直线约束的方法固定宽巷模糊度；L1、L2双差观测数据结合空间直线约束固定L1、L2双差模糊度。
上述6种方案采用不同的初始坐标计算方法，方案1直接采用伪距差分获取，其基线残差平均为41.6cm；方案2、3采用约束下的伪距差分，分别采用了直线约束和平面约束，其基线残差平均为34.3cm及13.5cm；方案4采用宽巷组合获得近似坐标，其基线残差平均为3.1cm；方案5、6采用约束下的宽巷组合获得，分别采用了直线约束和平面约束，其基线残差平均为3.8cm及3.0cm。由于宽巷组合本身定位精度较高，本试验约束条件强度较弱，对坐标精度改善有限，所以方案4、5、6的浮点解精度基本一致。
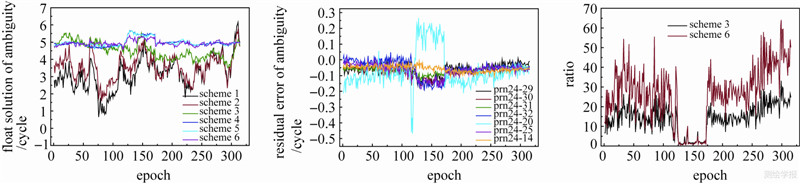
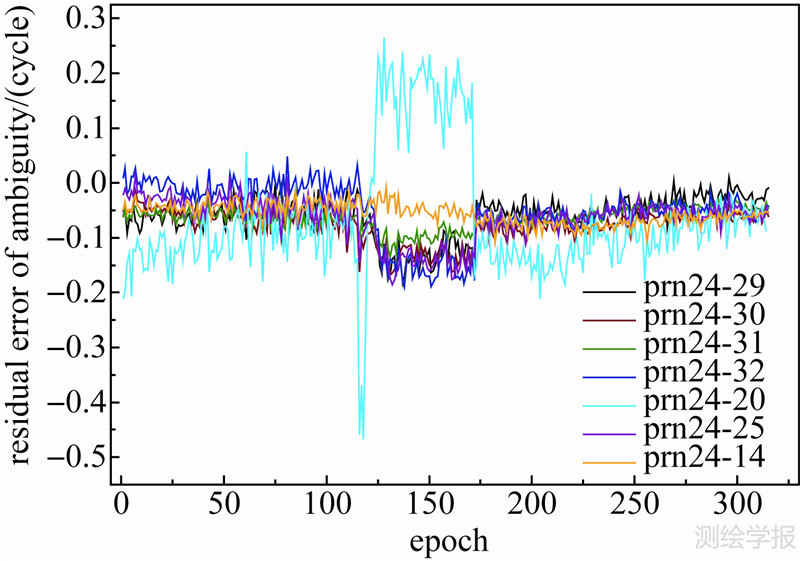
在该观测时段内，高度角在15°以上的卫星共有8颗，以高度角最大的24号卫星为参考卫星，L1、L2分别有7个双差模糊度。现以20号卫星为例，在第116历元接收机未能记录该卫星的数据，在其余314个历元中，用LGO解算的坐标反算其双差模糊度为5，由6种方案计算的L1模糊度浮点解如图 4所示。由图 4可知，方法1计算的模糊度浮点解精度最差，偏离模糊度正确值的最大值接近4.4周；方法6偏差最小，最大偏差为0.4周。这说明，通过宽巷组合结合线路约束条件，初始坐标精度得到改善，模糊度浮点解的精度也得到了提高。其他6颗卫星的双差模糊度浮点解也有类似情形。用LGO解算的坐标反算7颗卫星的双差模糊度，与正确值的差值如图 5所示，在第117至172历元之间偏差较大，这主要是由于在此期间道路旁高层建筑物的遮挡，导致观测数据质量较差。
|
| 图 4 L1模糊度浮点解(PRN24-20) Fig. 4 Float ambiguity of L1(PRN24-20) |
|
| 图 5 LGO反算模糊度浮点解与真值之差 Fig. 5 The difference between float Ambiguity resolved by LGO and the true value |
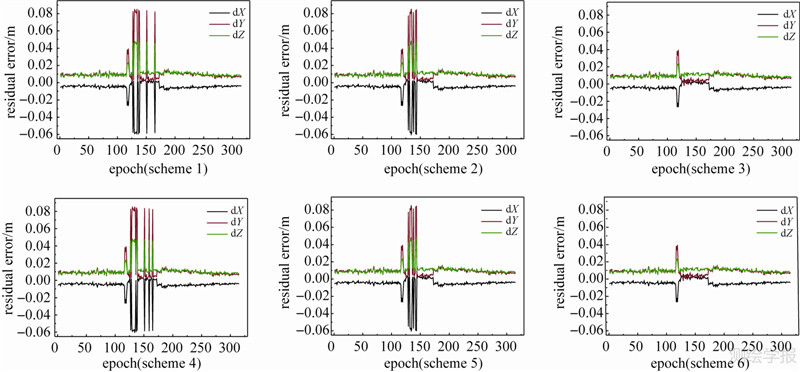
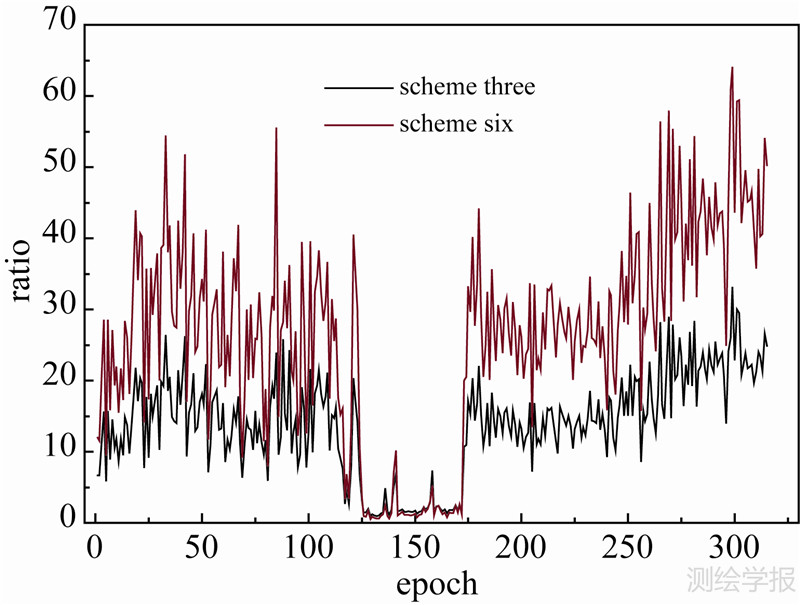
将LGO解算的结果视为真值，将这6种方案解算的坐标与真值求差，得到的真误差如图 7所示，方案1、2、4、5中出现的异常是模糊度解算失败所导致的。由图 7可以看出，从方案1到方案3，从无约束到引入平面约束，再到引入空间直线约束，由于模糊度浮点解得到改善，模糊度分解的成功率得到了提高，方案4到方案6也有类似的情形；方案1和方案4相比，成功率略有下降，这说明即使初始坐标较为精确，但由于多余观测较少、观测质量较差，利用LAMBDA方法得到的最优和次优模糊度难以区分。方案2和方案5、方案3和方案6解算成功率一致，方案3和方案6模糊度解算全部成功，这两种解算方案的Ratio如图 6所示。由图 6可见，方案6的Ratio值得到了提高。
|
| 图 7 6种方案坐标真误差 Fig. 7 The true error of coordinates about six methods |
|
| 图 6 方案3与方案6的ratio 值比较 Fig. 6 The ratios comparison of scheme 3 and scheme 6 |
以上分析表明第6种方案最优，主要有3个原因：① 宽巷模糊度固定后，未知数个数减少，只需固定L1的模糊度及坐标改正数，等价于多余观测数增加，改善了法方程的状态；② 以宽巷模糊度固定后解算的坐标作为坐标初始值，其精度较高，提高了L1模糊度浮点解的精度；③约束条件的加入，进一步改善了法方程的条件数，模糊度可区分性得到进一步提高。
模糊度固定后，将其作为已知值代入误差方程，去掉附加的轨迹约束条件，重新解算出坐标未知数。由于这6种方案只是在固定模糊度的方法上不同，在模糊度固定后，坐标解算都是只采用载波相位观测数据，如果模糊度解算成功，6种方案的坐标也是相同的。计算结果表明X方向的偏差在5mm左右，Y和Z方向偏差在9mm左右，在117到120的4个历元，出现较大偏差，这主要是由于在此期间20号卫星在接收到的8颗卫星中高度角最小，其观测数据质量较差，影响了定位精度，这可以从图 5中看出，用LGO反算模糊度与正确值偏差达0.4周。
需要说明的是，以上的分析结果，是在构造约束条件时，共用17段直线、圆曲线来拟合轨迹，轨迹点偏离拟合线形的平均值是2.9cm，最大值为7.7cm，当用17个平面来拟合轨迹时，轨迹点偏离平面的距离平均值是2.3cm，最大值为6.5cm的情况下得到的。为了检验不同约束强度对解算结果的影响，采用12段直线、圆曲线来拟合，距离偏差的平均值是4.6cm，最大值为11.5cm，当用12个平面来拟合轨迹时，距离偏差平均值是3.9cm，最大值为11.0cm。再次进行解算，两种不同约束强度下的解算成功率如表 1所示。从表中可以看出，随着约束强度的减弱，4种约束方案的解算成功率出现了下降，但方案6仍然保持着很高的成功率。
| 约束强度/cm | 成功历元数 | 成功率/(%) | 约束强度/cm | 成功历元数 | 成功率/(%) | |
| 方案1 | N/A | 304 | 96.51 | N/A | — | — |
| 方案2 | 2.3 | 307 | 97.46 | 3.9 | 263 | 83.49 |
| 方案3 | 2.9 | 315 | 100.00 | 4.6 | 303 | 96.19 |
| 方案4 | N/A | 302 | 95.87 | N/A | — | — |
| 方案5 | 2.3 | 307 | 97.46 | 3.9 | 275 | 87.30 |
| 方案6 | 2.9 | 315 | 100.00 | 4.6 | 311 | 98.73 |
| 注：N/A表示该方案未用约束条件 | ||||||
(1) 根据线路的设计数据、利用较短的直线段逐段地替代圆曲线和缓和曲线，动态地构建轨迹约束条件，计算简便，精度可靠。空间直线约束属于三维约束，其强度高于二维平面约束，但即使附加二维平面轨迹约束后，近似坐标的精度也得到显著改善，模糊度的可区分性得到了提高。
(2) 即使在没有约束条件的动态单历元情况下，宽巷模糊度固定后解算的坐标其精度较高，采用方案4(先宽巷组合按照阻尼LAMBDA方法解算，再固定L1、L2模糊度解算)能获得很高的解算成功率，比方案1(直接采用L1、L2双差观测数据按照阻尼LAMBDA方法解算)的模糊度可区分性要好。
(3) 在短基线情况下，多路径误差和观测噪声成为制约单历元精度的主要因素，如何削弱动态环境下的多路径误差是下一步将要研究的问题。
| [1] | LIU Genyou. A New Method of Determining Attitude with GPS: Damped LAMBDA Algorithm with Coordinates Functional Constraint[J]. Science of Surveying and Mapping, 2003, 28(3):36-38. (刘根友. 一种GPS测定姿态的新方法[J]. 测绘科学, 2003, 28(3): 36-38.) |
| [2] | XIONG Yongliang, HUANG Dingfa, ZHANG Xianzhou. A Reliable GPS Single Epoch Processing Algorithm with Known Deformation Interval Constraints [J]. Geomatics and Information Science of Wuhan University, 2001, 26(1):51-56. (熊永良, 黄丁发, 张献洲. 一种可靠的含有约束条件的GPS变形监测单历元求解方法[J]. 武汉大学学报: 信息科学版, 2001, 26(1): 51-56.) |
| [3] | HAN Baomin, OU Jikun. A GPS Single Epoch Phase Processing Algorithm with Constraints for Single-frequency Receiver[J]. Acta Geodaetica et Cartographica Sinica. 2002, 31(4): 300-304. (韩保民, 欧吉坤. 一种附约束的单频单历元GPS双差相位解算方法[J]. 测绘学报, 2002, 31(4): 300-304.) |
| [4] | MOK E. Reliable Single Epoch GPS Processing Algorithm for Static Deformation Monitoring[J]. Geomatics Research Australia, 1999, 70: 95-117. |
| [5] | CHEN Yongqi, LUTES J. Development of the Methodology for Single Epoch GPS Deformation Monitoring[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1998, 23(4): 324-328. (陈永奇, LUTES J . 单历元GPS变形监测数据处理方法的研究[J]. 武汉测绘科技大学学报, 1998, 23(4): 324-328.) |
| [6] | DAI Wujiao, ZHU Jianjun, DING Xiaoli, et al. Single Epoch Ambiguity Resolution in Structure Monitoring Using GPS[J]. Geomatics and Information Science of Wuhan University, 2007, 32(3): 234-241. (戴吾娇, 朱建军, 丁晓利, 等. GPS建筑物振动变形监测中的单历元算法研究[J]. 武汉大学学报:信息科学版, 2007, 32(3): 234-241. ) |
| [7] | YU Xuexiang, XU Shaoquan, LU Weicai. The Research of Single Epoch Algorithm for the GPS Deformation Monitor Information[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(2): 123-127. (余学祥, 徐绍铨, 吕伟才. GPS变形监测信息的单历元解算方法研究[J]. 测绘学报, 2002, 31(2): 123-127.) |
| [8] | HAN S W, RIZOS C. Single-epoch Ambiguity Resolution for Real-time GPS Attitude Determination with the Aid of One-dimensional Optical Fiber Gyro[J]. GPS Solutions, 1999, 3(1): 5-12. |
| [9] | TEUNISSEN P J G, GIORGI G, BUIST P J. Testing of a New Single-frequency GNSS Carrier Phase Attitude Determination Method: Land, Ship and Aircraft Experiments[J]. GPS Solutions, 2011, (15):15-28. |
| [10] | CHEN W T, QIN H L. New Method for Single Epoch, Single Frequency Land Vehicle Attitude Determination Using Low-end GPS Receiver[J]. GPS Solutions, 2012, (16): 329-338. |
| [11] | TEUNISSEN P J G. The LAMBDA Method for the GNSS Compass[J]. Art Satellites, 2006, 41(3): 89-103. |
| [12] | TEUNISSEN P J G. Integer Least Squares Theory for the GNSS Compass[J]. Journal of Geodesy, 2010, (84): 433-447. |
| [13] | LIU Genyou, OU Jikun. Kinematic Positioning Algorithm with Coordinate Function Constraint[J]. Geomatics and Information Science of Wuhan University, 2004, 29(5): 389-393. (刘根友, 欧吉坤. 具有坐标函数约束的动态定位算法[J]. 武汉大学学报: 信息科学版, 2004, 29(5): 389-393.) |
| [14] | TANG Weiming, SUN Hongxing, LIU Jingnan. Ambiguity Resolution of Single Epoch Single Frequency Data with Baseline Length Constraint Using LAMBDA Algorithm[J]. Geomatics and Information Science of Wuhan University, 2005, 30(5): 444-446. (唐卫明, 孙红星, 刘经南. 附有基线长度约束的单频数据单历元LAMBDA方法整周模糊度确定[J]. 武汉大学学报: 信息科学版, 2005, 30(5): 444-446.) |
| [15] | ZHU Huizhong, GAO Xingwei, XU Aigong, et al. Single-epoch Ambiguity Resolution for Network RTK Rovers[J]. Science of Surveying and Mapping, 2010, 35(2): 77-79. (祝会忠, 高星伟, 徐爱功, 等. 网络RTK流动站整周模糊度的单历元解算[J]. 测绘科学, 2010, 35(2): 77-79.) |
| [16] | LI Quanxin. General Mathematical Model for the Highway Central Line Coordinate Computation[J]. Site Investigation Science and Technology, 2001(5): 43-47. (李全信. 线路中线坐标计算的通用数学模型[J]. 勘察科学技术, 2001(5): 43-47.) |
| [17] | WANG Jiexian, WANG Jun, LU Caiping. Problem of Coordinate Transformation between WGS-84 and BEIJING 54[J]. Journal of Geodesy and Geodynamics, 2003, 23(3): 70-73. (王解先, 王军, 陆彩萍. WGS-84与北京54坐标的转换问题[J]. 大地测量与地球动力学, 2003, 23(3): 70-73.) |
| [18] | TEUNISSEN P J G. The Least-squares Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy, 1995,70(1-2): 65-82. |
| [19] | KUBO N. Advantage of Velocity Measurements on Instantaneous RTK Positioning[J]. GPS Solutions, 2009, 13(4): 271-280. |
| [20] | JI S Y, CHEN W, ZHAO C M, et al. Single Epoch Ambiguity Resolution for Galileo with the CAR and LAMBDA Methods[J]. GPS Solutions, 2007, 11(4): 259-268. |
| [21] | PARKINS A. Increasing GNSS RTK Availability with a New Single-epoch Batch Partial Ambiguity Resolution Algorithm[J]. GPS Solutions, 2011, 15(4): 391-402. |