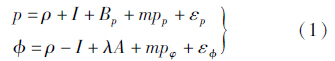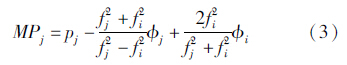2. 武汉大学 测绘学院,湖北 武汉 430079
2. School of Geodesy and Geomatics, Wuhan University, Wuhan, 430079, China
1 引 言
自2000年发射第1颗试验卫星以来,北斗导航系统(BeiDou)就已引起极大的关注;截止本文完成,北斗系统已包含3颗GEO和3颗IGSO卫星。可以预见,当北斗系统正式建成后,将在定位、导航、授时、通讯等多领域发挥重要作用[1, 2, 3, 4]。
目前,基于北斗系统的研究主要集中于信号结构、定位定轨、时频转换等[1, 5, 6, 7, 8, 9, 10];北斗测距信号质量是服务于上述应用的基础,但与之相关的研究却尚未有效深入。
借鉴以往零/短基线分析GPS测距信号质量的思路[11, 12, 13, 14, 15, 16, 17],基于约1 h的实测短基线数据,本文设计不同方案,对比分析了GPS和北斗测距信号,量化了有关的观测噪声和多路径误差,并检验了相关的影响因素;基于不同时长的双差数据,考察了多路径误差对CC模糊度固定的影响。
2 方 法 2.1 观测方程GPS/北斗的伪距和相位方程均可表示为
式中,p和Φ分别为伪距和相位观测;ρ为与频率无关项;Bp为伪距硬件延迟;I为电离层斜延迟;mpp、mpΦ分别为伪距和相位多路径误差;A为含初始相位偏差的模糊度参数,λ为波长因子;εp,εΦ分别表示两类观测值的观测噪声,且满足E{ε}=0。由式(1)可导出如下两类组合观测值,用以分析测距信号质量:
(1) 伪距相位差值组合(Code-minus-phase Combination,CC),具体形式为
式(2)中假定相位观测噪声和多路径误差远小于伪距,等式右侧将主要受伪距噪声和多路径误差支配。
(2) MP组合,可用于单独考察对应于频段j的伪距多路径误差,且表达式为
其中,i,j为相位观测值的频段,且i≠j。 2.2 单测站分析方案为便于分析,式(2)和(3)所含的非零期望值须事先移除。针对单站数据分析,此处采用如下两种方案。
2.2.1 低阶多项式拟合低阶多项式拟合可消除式(2)中随时间缓慢变化的量,如伪距硬件延迟[18]、模糊度、低频多路径误差和电离层延迟等。移去拟合值后,余项将主要包含伪距噪声、高频多路径误差以及残余电离层延迟等,相关期望和方差分别为
其中,p(t)为低阶多项式拟合值;σp为伪距的标准差;dI和dmpp分别对应残余的电离层和伪距多路径误差。针对1 s间隔的观测数据,根据文献[13, 14]建议,本文选用120个数据(即2 min)采用实施多项式拟合,以尽可能降低拟合误差。对应于式(3)的期望和方差分别为
易知,当不存在周跳时,式(5)期望表达式中所含的模糊度和伪距硬件延迟均可通过取平均加以移除,此后的时间序列将主要受伪距多路径误差影响。
2.2.2 历元间差分针对高频采样观测值,对CC组合实施相邻历元间差分,可消除模糊度常数,并大大削弱电离层延迟、多路径误差和伪距硬件延迟,对应的期望和方差分别为
其中,Δ表示相邻历元间的差分;ρΔ是相邻历元伪距的相关系数(|ρΔ|<1),本文合理假定ρΔ在一段时间内(如120 s)保持不变。同样地,相邻历元间的MP组合观测值差分,可消除模糊度,并显著移除伪距硬件延迟的影响,其期望和方差为
需要指出,由于多路径短期内(如1 s)内变化不大,历元间差分还可有效抵消多路径误差,因此,式(6)和(7)的期望值序列将主要反映测距信号的随机性质。
2.3 短基线分析方案 2.3.1 站间单差在短基线测量中,2个测站至同一卫星的大气延迟相等;但所受多路径误差影响却不相同[19]。此处仅分析CC观测值,对应站间单差结果的期望和方差为
其中,ρSD为两测站伪距观测值的相关系数,对于短基线测量,两台接收机观测噪声的相关系数较小,即[ρSD]SB≈0。当不存在周跳时,单差观测值减去平均值可消除模糊度,并削弱站间单差的接收机硬件延迟。类似地,对站间单差CC观测值实施相邻历元间差分,可消除模糊度常数,削弱伪距硬件延迟和多路径误差,对应的期望和方差为
2.3.2 站星双差对不同卫星的站间单差CC观测值作差,可进一步形成双差观测值,且主要含整周模糊度、码观测噪声和伪距多路径误差。不同卫星的观测噪声不相关,因此双差CC观测值的期望和方差为
表 1对前述各类观测值进行了归纳和分类,概括了各自的性质、处理策略等。其中,第1组观测值可直接计算出观测噪声σp2,但仅采用拟合和取平均的方法并不能消除周期性的多路径误差;第2组观测值有效克服了多路径误差的影响,从而可更精确地还原观测噪声σp2。
| 分组 | 试验 | 差分 | 组合 | 期望 | 改正方法 | 方差 |
| 1 | 1Rx | UD | CC | 2I+A+mpp+εp | 拟合 | σp2 |
| 1Rx | UD | MP | mp+Amp+εmp | 取平均 | σp2 | |
| SB | SD | CC | mpSD+ASD+εSD | 取平均 | 2σp2 | |
| SB | DD | CC | λNDD+mpDD | 取平均 | 4σp2 | |
| 2 | 1Rx | △ | CC | 2ΔI+Δmpp | — | 2(1-ρΔ)σp2 |
| 1Rx | △ | MP | Δmpp | — | 2(1-ρΔ)σp2 | |
| SB | △SD | CC | ΔmpSD | — | 4(1-ρΔ)σp2 | |
| SB | △DD | CC | ΔmpDD | — | 8(1-ρΔ)σp2 |
本文选用2010-12-27的短基线(长度约为3.3 m)实测数据,分属于GPS L1/L2、北斗B1/B2 4个频率、3类卫星(GPS为MEO卫星,北斗包括GEO和IGSO卫星),观测时长约1 h,采样间隔为1 s。本节首先分析了各卫星、各频率的观测噪声和多路径误差,并检验了多路径对CC模糊度固定成功率的影响。
3.1 观测噪声以某测站至GPS PRN5的L1 CC观测值为例,图 1中前两幅子图分别为移除多项式拟合值以及历元间差分后的结果(后文分别用CC1和△CC1代称),下图为对应的信噪比。易知在1小时的观测时段中,CC1值存在周期性的变化,主要归因于多项式拟合未完全消除伪距多路径误差。

|
| 图 1 单站GPS PRN05 L1频率上CC值 Fig. 1 Stand alone code-minus-phase combination for GPS PRN05 at L1 |
将观测时间段均匀地划分为30组,每组含120历元,用于计算伪距标准差。图 2首先给出了各类卫星伪距标准差与信噪比的关系。其中,GPS卫星信噪比在42~52 dB-Hz之间,而北斗GEO卫星的信噪比主要集中在42~45 dB-Hz,IGSO卫星的信噪比较GEO卫星高,均分布在46~50 dB-Hz。

|
| 图 2 单站不同卫星的码观测值标准差与信噪比分布图,S/N0=45 (dB-Hz),时间段为120 s Fig. 2 Stand alone receiver code-minus-phase standard deviation verse S/N0 for different kinds of satellites,for S/N0 = 45 (dB-Hz) and with data segments of 120 s |
为定量衡量伪距观测噪声与信噪比的关系,选用曲线拟合不同信噪比下的标准差,曲率表示在信噪比为45 dB-Hz的观测值方差,拟合结果如图 2中实线所示,而标准差的统计信息见表 2。为便于比较,同样基于表 1中的其余观测类型计算伪距标准差,结果见表 2。
| m | ||||||
| 线性 观测值 |
GPS L1 C/A |
GPS L2 P2 |
Compass B1 | Compass B2 | ||
| MEO | MEO | GEO | IGSO | GEO | IGSO | |
| UD CC | 0.058 | 0.017 | 0.033 | 0.099 | 0.034 | 0.111 |
| UD MP | 0.059 | 0.018 | 0.034 | 0.099 | 0.035 | 0.112 |
| SD CC | 0.072 | 0.034 | 0.032 | 0.099 | 0.033 | 0.116 |
| △CC | 0.022 | 0.012 | 0.015 | 0.042 | 0.016 | 0.045 |
| △MP | 0.025 | 0.015 | 0.016 | 0.042 | 0.020 | 0.047 |
| △SD CC | 0.030 | 0.014 | 0.014 | 0.038 | 0.015 | 0.046 |
表 2结果显示,针对所有卫星在4个频率上的测距信号,CC组合与MP组合计算的标准差大致相同,表明本文采用二阶多项式拟合能较好的消除CC组合上的电离层延迟;比较GEO和IGSO的标准差计算值可知,在同一频率上,IGSO的标准差约为GEO的3倍,原因可能为GEO卫星相对于测站是“静止的”,而IGSO卫星是运动的,存在着多普勒效应,且IGSO测距信号的信噪比较高;GPS L2频率的伪距标准差最小,达0.02 m左右,而北斗IGSO卫星B2频率上伪距标准差最大;北斗GEO卫星的观测精度为0.03~0.04 m,北斗IGSO卫星的观测精度约为0.10~0.12 m。
结合表 1可知,第1组中各方法略差,因为多项式拟合或取平均无法保证多路径、电离层、伪距硬件延迟的充分削弱;基于高采样率的数据,如本文中的1 s采样率,历元间差分方法最好(本文中第2组方案),其充分消除了前述各种延迟和多路径误差。因此在选用检验方法时,可根据实验条件,选择短基线方法,如考虑到成本和维护费用,也可选择单站检验。
3.2 多路径误差前文已述,部分系统误差如多路径效应,在单站和短基线观测中均不能完全移除,本节对表 1中不同观测类型的多路径作进一步分析。图 3、图 4分别表示北斗B1/B2的MP1和MP2及对应的信噪比。

|
| 图 3 北斗卫星B1频率的MP12组合与信噪比图 Fig. 3 MP12 combination and S/N0 for BeiDou satellites at B1 |

|
| 图 4 北斗卫星B2频率的MP21组合 Fig. 4 MP12 combinations for BeiDou satellites at B2 |
文献[20, 21, 22]指出了GPS多路径误差与信噪比的负相关性,由表 1知多路径组合取平均后移除了模糊度常数及多路径误差的常数项,仅残余周期性的多路径误差。从图中可看出,北斗多路径组合值与信噪比亦呈负相关的关系;GEO卫星的多路径组合变化范围较大(-1 m~+1.2 m),呈现长期变化的趋势;而IGSO卫星的多路径组合变化范围较小(-0.6 m~+0.6 m),呈现短期变化的趋势。文献[8, 9]报告了类似的实验结果,但与之相关的机制尚未明确。
图 5、图 6分别表示北斗卫星在B1和B2频率上CC组合的站间单差,上下分别表示GEO和IGSO卫星。从图中可知,站间单差值受较小的多路径误差影响(与相应的单站结果相比);GEO卫星呈现长期变化,其在两个频率上的变化均在-0.3 m~+0.3 m间;而IGSO呈现短期变化的趋势,其变化范围从-0.6 m~+0.6 m。

|
| 图 5 北斗卫星B1频率上CC组合的站间单差 Fig. 5 Single difference code-minus-phase observations for BeiDou satellites at B1 |

|
| 图 6 北斗卫星B2频率上CC组合的站间单差 Fig. 6 Single difference code-minus-phase observations for BeiDou satellites at B2 |
为比较北斗系统两类卫星的模糊度特性,分别以GEO卫星和IGSO卫星为基准星,组成双差观测值,进而可确定出GEO和IGSO卫星CC组合的双差模糊度,如图 7、图 8所示。从图中可知,GEO卫星的双差CC值变化缓慢,而IGSO卫星的结果中则存在明显的变化趋势。B2信号的CC模糊度变化范围更小,表明其更易固定到整数。

|
| 图 7 北斗GEO卫星CC组合双差模糊度与信噪比图 Fig. 7 Double Difference code-minus-phase ambiguity and S/N0 for BeiDou GEO satellites |

|
| 图 8 北斗IGSO卫星CC组合双差模糊度与信噪比图 Fig. 8 Double Difference code-minus-phase ambiguity and S/N0 for BeiDou IGSO satellites |
对于图 7、图 8中双差CC值的时间序列,取120 s和600 s数据一组,若每组双差CC值的均值减去真值后小于0.5周,即可认为模糊度可通过四舍五入取整加以准确固定。表 3表示CC组合在GPS L1、L2、北斗B1和B2频率上模糊度固定的成功率,其中,针对600 s时长,4个频率上模糊度固定均能达到90%以上;而对于120 s时长,由于多路径误差不能完全的移除,模糊度固定成功率不高;考虑到IGSO卫星多路径误差短期快速变化的趋势和较差的观测精度,其模糊度固定的成功率最低(均不超过50%),这也与上面的分析一致。
| (%) | |||||||
| 时间段/s | GPS | Compass | |||||
| L1 | L2 | B1- GEO |
B2- GEO |
B1- IGSO |
B2- IGSO |
||
| SB | 120 | 67.2 | 76.0 | 59.2 | 75.7 | 41.4 | 48.8 |
| 600 | 96.8 | 92.9 | 93.2 | 94.3 | 92.7 | 93.8 | |
本文通过实测的GPS/北斗双系统短基线数据,采用非差、单差、双差CC和MP组合观测值,分析北斗系统在B1和B2频率上的观测噪声,并与相应的GPS结果进行比较分析。结果表明:
(1) 北斗系统中,GEO卫星在2个频率上的精度均优于IGSO卫星,两类卫星的观测精度分别为0.03 m~0.04 m、0.10 m~0.12 m。
(2) GEO卫星的多路径组合变化范围较大(-1 m~+1.2 m),呈现长期变化的趋势;而IGSO卫星的多路径组合变化范围较小(-0.6 m~+0.6 m),呈现短期变化的趋势。
(3) 采用较长时间段固定单频CC组合的模糊度,如本文中的600s,4个频率上模糊度固定成功率均能达到90%以上;当采用较短时间观测数据时(如120 s),由于IGSO卫星多路径效应短期变化的趋势和较差的观测精度的影响,其模糊度固定的成功率最低,B1、B2频率均不超过50%。
当然,本文的统计性质只能反映某类接收机的数据质量,不具有普遍性。但对以后分析北斗卫星的数据质量和接收机的观测质量,以及定量的比较GPS系统与北斗系统奠定了理论基础。
| [1] | YANG Yuanxi. Process, Contribution and Challenges of Compass/Beidou Satellite Navigation System [J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1-5. (杨元喜.北斗卫星导航系统的发展、贡献与挑战[J].测绘学报,2010,39(1):1-5.) |
| [2] | TAN Shusen. Engineering for Satellite Navigation Position [M]. Beijing: The National Defense Industry Press, 2007. (谭述森.卫星导航定位工程[M].北京:国防工业出版. 2007.) |
| [3] | DANG Yamin, BI Jinzhong, CHENG Yingyan. Principles and applications of Global Navigation Satellite System [M]. Beijing: Surveying and Mapping Press, 2007. (党亚民,秘金钟,成英燕.全球导航与卫星系统原理与应用[M].北京,测绘出版社,2007.) |
| [4] | CHEN Junyong, ZHANG Peng, WU Junli, et al. On Chinese National Continuous Operating Reference Station System of GNSS [J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(4): 366-369. (陈俊勇,张鹏,武军郦,等.关于在中国构建全球导航卫星国家级连续运行站系统的思考[J].测绘学报,2007,36(4): 366-369.) |
| [5] | WANG Lei, ZHAI Guojun, HUANG Motao, et al. A New Analytic Solution for Beidou Passive Postioning in Sea[J]. Geomatics and Information Science of Wuhan University, 2008, 33(6):635-638. (王磊,翟国君,黄谟涛,等.北斗海上无源定位解析求解新方法[J].武汉大学学报:信息科学版,2008,33(6):635-638). |
| [6] | LIN Xueyuan. Synthetical Error Analysis and Simulation for Double-Star Position System [J]. Geomatics and Information Science of Wuhan University, 2009, 34(9):1110-1112. (林雪原.双星定位系统的综合误差分析与仿真[J].武汉大学学报:信息科学版,2009,34(9):1110-1112.) |
| [7] | WAN Xiang, ZHANG Mengyang. High Dynamics Dual-frequency Relative Positioning with Beidou System [J]. Journal of Spacecraft TT&C Technology, 2010, 29(3):68-73. (万祥,张孟阳.北斗高动态双频相对定位技术[J].飞行器测控学报,2010,29(3):68-73.) |
| [8] | HAUSCHILD A, MONTENBRUCK O, SLEEWAEGEN J M, et. al. Characterization of Compass M-1 signals[J]. GPS Solutions, 2012(16):117-126. |
| [9] | ANSELMO L, PARDINI C. Orbital Evolution of the First Upper Stages Used for the New European and Chinese Navigation Satellite Systems [J]. Acta Astronautica, 2011, 68:2066-2079. |
| [10] | HAN C H, YANG Y X, CAI Z W. Beidou Navigation Satellite System and Its Time Scales [J]. Metrologia, 2011(48):213-218. |
| [11] | TIBERIUS C C J M. KENSELAAR F. Estimation of the Stochastic Model for GPS Code and Phase Observables [J]. Survey Review, 2000(35):441-454. |
| [12] | AMIRI-SIMKOOEI A R, TIBERIUS C C J M. Assessing Receiver Noise Using GPS Short Baseline Time Series [J]. GPS Solutions, 2007,11:21-35. |
| [13] | BAKKER P F DE, MAREL H VAN DER, TIBERIUS CHRISTIAN C C J M. Geometry-free Undifferenced, Single and Double Differenced Analysis of Single Frequency GPS, EGNOS and GIOVE-A/B Measurements [J]. GPS Solutions, 2009, 13:305-314. |
| [14] | BAKKER P F DE, TIBERIUS C C J M, MAREL H VAN DER, et al. Short and Zero Baseline Analysis of GPS L1 C/A, L5Q, GIOVE E1B, and E5aQ Signals [J]. GPS Solutions, 2012,16(1):01-05. |
| [15] | JONKMAN N F. The Geometry-Free Approach to Integer GPS Ambiguity Estimation [C]//Proceedings of ION GPS, [S.l.]: ION GPS, 1998. |
| [16] | LIU J, CANNON M E, ALVES P, et al. A Performance Comparison of Single and Dual Frequency GPS Ambiguity Resolution Strategies [J]. GPS Solutions, 2003, 7:87-100. |
| [17] | TEUNISSEN P J G. The Geometry-free GPS Ambiguity Search Space with a Weighted Ionosphere [J]. Journal of Geodesy, 1997, 71(6):370-383. |
| [18] | LIU X, TIBERIUS C C J M, DE JONG K. Modelling of Differential Single Difference Receiver Clock Bias for Precise Positioning [J]. GPS Solutions, 2004, 7(4):209-221. |
| [19] | ZHANG Baocheng, OU Jiekun, Yuan Yunbin, et al. Calibration of Slant Total Electron Content and Satellite-receiver’s Differential Code Biases with Uncombined Precise Point Positioning Technique [J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 447-453. (张宝成,欧吉坤,袁运斌,等.利用非组合精密单点定位技术确定斜向电离层总电子含量和站星差分码偏差 [J].测绘学报,2011,40(4): 447-453). |
| [20] | AXELRAD P, COMP C J, MACDORAN P F. SNR-based Multipath Error Correction for GPS Differential Phase [J]. IEEE transaction on Aerospace and Electronic Systems, 1996, 32(2): 650-660. |
| [21] | 夏林元. GPS观测值中的多路径效应理论及数值结果 [D].武汉:武汉大学,2001. |
| [22] | WU Yuhang, CHEN Xiuwang, WU Caicong. Mitigation of Multipath Effect using SNR Values [J]. Geomatics and Information Science of Wuhan University, 2008, 33(8): 842-845. (吴雨航,陈秀万,吴才聪.利用信噪比削弱多路径误差的方法研究[J].武汉大学学报:信息科学版,2008,33(8):842-845.) |