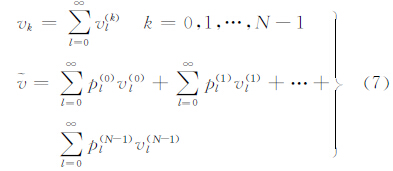2. 武汉大学 地球空间环境与大地测量教育部重点实验室，湖北 武汉 430079
2. Key Laboratory of Geospace Environment and Geodesy of Ministry of Education, Wuhan University, Wuhan 430079, China
1 引 言
欧空局研制的GOCE卫星于2009-03-17成功发射，它联合了高低卫-卫跟踪(SST-hl)和卫星重力梯度测量(SGG)技术，其目标是以100 km 空间分辨率、1～2 cm大地水准面精度测定全球静态地球重力场[1]。在GOCE任务中，SST-hl和SGG观测数据的精度与频谱特性具有明显差异性，它们在恢复重力场方面各有所长并互为补充。其中，SST-hl技术是基于卫星轨道摄动反演地球重力场，由于重力场信号随卫星高度的增加而快速衰减，分析轨道摄动仅能精确获得低频重力场信息；SGG技术直接测定引力位的二阶导数，在一定程度上可补偿重力场信号随卫星高度增加而产生的衰减，有利于高精度测定中高频重力场信号。因此，如何有效利用这两类不同精度和反映重力场不同频谱特性的观测数据来反演高精度、高分辨率地球重力场模型，是GOCE重力场反演中迫切需要解决的问题。
目前欧空局公布的GOCE系列模型主要采用了3种解法[2]：时域法、空域法和直接法。时域法将观测值看成沿卫星轨道的时间序列，采用能量法建立SST-hl观测方程，并基于Kaula轨道摄动分析理论建立SGG观测方程，然后将这两类观测方程进行联合平差求解重力场位系数[3, 4]。空域法将GOCE获得的沿轨扰动位和重力梯度分量数据作为卫星位置的函数，并将其归算至平均轨道球面上形成规则的格网数据，采用最小二乘配置法联合求解重力场位系数[5, 6]。直接法是在卫星位置处直接建立重力梯度观测值与引力位系数的严密数学关系，并将其形成的SGG观测方程和基于动力学法建立的SST-hl观测方程进行联合平差，然后经过多次迭代求解重力场位系数[2, 7]。上述3种解法主要采用最小二乘配置法和最小二乘联合平差法对GOCE SST-hl和SGG数据进行联合求解。其中，配置法是将地球重力异常场视为一球面的平稳随机过程，通过各种重力场参量与扰动位之间的协方差函数求解扰动位的最优估计。配置法的最大特点是能够综合处理多种重力观测数据，但它需要精确估计重力场参量之间的协方差函数，并存在超高阶协方差矩阵的求逆问题，这在海量数据处理中受到了限制。最小二乘联合平差是将各类独立观测值建立的观测方程进行联合平差解算，并采用方差分量估计[8, 9]对观测值进行定权。联合平差处理的关键是对各类观测值进行合理定权，由于方差分量估计是一种迭代定权的过程，因而对海量卫星重力数据的处理极为耗时。例如，直接法仅通过各类观测值求解的验后方差信息进行经验定权[2]。此外，配置法和联合平差法在联合求解过程中难以显式地顾及各类观测数据的频谱差异性。
为了有效顾及各类观测数据的精度和频谱特性进行最优联合求解，本文研究了联合SST-hl和SGG数据恢复地球重力场的最小二乘谱组合法。谱组合法是一种兼顾解析和统计特性的方法，它将各类观测数据对位系数的谱贡献作最小二乘加权组合，已被有效应用于多种重力数据的联合处理[10, 11, 12, 13]。由于通过能量守恒方程可将SST-hl测量提供的卫星精密轨道和非保守力加速度计数据转化为沿轨扰动位[6, 14]，因此本文以卫星平均轨道球面为边界面，基于球谐分析方法推导并建立联合扰动位T和径向重力梯度Tzz、以及扰动位T和重力梯度分量组合{Tzz－Txx－Tyy}恢复重力场的谱组合计算模型与误差估计公式。该计算模型不仅可以显式地顾及各类数据的精度和频谱特性进行最优联合求解，而且具有计算快速的特点。最后，通过数值模拟计算和GOCE实测数据解算，对建立的谱组合计算模型进行了分析和验证。
2 谱组合原理假设利用两种不同类型的重力观测数据分别得到了重力场参量v的无偏估计值，其级数展开式为
式中，vk表示由两类观测数据分别估计得到的重力场参量，vl(k)为其 l 阶谱分量。采用以下线性无偏估计模型确定重力场参量v的最优估值[10] 式中，pl为谱分量vl(0)的权；(1－pl)为谱分量vl(1)的权，它们是与位系数阶数 l 相关的谱权。由误差传播定律可得到线性无偏估值
的误差方差为
式中，
为l阶谱分量vl(k)的误差阶方差，σl,n(j,k)为l阶谱分量vl(j)和n阶谱分量vn(k)的误差互协方差。
根据最小二乘估计原理，要使得σ2=min成立，可采用一般求极小值的方法，将式(3)关于pl求偏导，并令其为0可得
l的估计误差分别为
类似于上述推导，可得到利用N类观测数据估计重力场参量v的谱组合解为
式中，pl(k)为谱分量vl(k)对应的谱权。在pl(0)+pl(1)+…+pl(N－1)=1的条件下，式(7)中各类观测数据的谱权和谱分量
l的估计误差为
根据权与误差方差成反比的关系，从式(7)和式(8)可以看出，谱组合解是将各类观测数据估计重力场参量v的谱分量vl(k)进行加权最小二乘估计的组合值，故又称为最小二乘谱组合。
3 谱组合计算模型
基于球谐分析方法，利用扰动位T和径向扰动重力梯度分量Tzz计算位系数的积分公式分别为
式中，R为地球平均半径；Rs为平均轨道球面半径；GM为地心引力常数；(θ,λ)为地心余纬和经度；
lm为规格化勒让德函数；σ为单位球面；dσ为积分面元。由于利用水平扰动重力梯度分量Txx、Tyy计算位系数的积分公式很难给出，但考虑到地球外部的重力梯度对角线分量满足拉普拉斯方程：Txx+Tyy+Tzz=0，因此，可给出利用扰动重力梯度分量组合{Tzz－Txx－Tyy}计算位系数的积分公式
式中，{Tzz－Txx－Tyy}=2Tzz，而{－Txx－Tyy}可认为是Tzz的“等效观测值”。
以下首先推导扰动位和径向重力梯度的谱组合计算模型。根据式(9)和式(10)可给出联合扰动位T和径向扰动重力梯度Tzz恢复重力场的谱组合公式为
式中，plT和(1-plT)分别是扰动位T和径向扰动重力梯度Tzz对应的谱权。可以看出，谱组合表达式(12)实质上等价于重力场模型位系数的谱组合 式中，{
lm;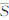
lm}(T)、{lm;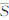lm}(Tzz)分别表示由观测数据T和Tzz确定的位系数；谱权plT可根据两类观测数据分别估计的位系数误差来确定。对于球面规则格网数据T和Tzz，若已知其精度信息(误差方差分别为m2{T}和m2{Tzz})，则根据误差传播定律由球谐分析公式可建立格网数据误差与位系数估计误差的解析关系[15, 16]。
根据误差传播定律，由式(9)可得
式中，m2{
lm;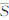lm}(T)表示由格网扰动位T估计位系数的误差方差。假设格网经差和纬差相等(Δθ=Δλ)，则有
，其中s为卫星平均轨道球面上格网方块的边长。顾及以下性质
则由式(14)可得到，利用等精度格网扰动位T估计位系数的误差方差为
同理，根据式(10)可以推导出格网径向扰动重力梯度Tzz与位系数的误差关系为
式中，m2{
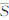lm;lm}(Tzz)表示由格网径向扰动重力梯度Tzz估计位系数的误差方差。根据两类观测数据的谱组合原理，可得到扰动位数据T的谱权为
将式(16)、式(17)代入式(18)，整理可得
最后，将式(19)代入式(13)可得到联合扰动位T和径向扰动重力梯度Tzz恢复重力场的谱组合计算公式为
并且，由式(6)可给上式估计位系数的误差方差为 在以上推导过程中将径向重力梯度分量替换为重力梯度分量组合，可得到联合扰动位T和扰动重力梯度分量组合{Tzz－Txx－Tyy}的谱组合计算模型与误差估计公式 式中，m2{Tzz－Txx－Tyy}表示由格网扰动重力梯度分量组合{Tzz－Txx－Tyy}估计位系数的误差方差。 4 计算与分析 4.1 数值模拟与分析
利用EIGEN-5C模型模拟计算平均轨道高度为250 km球面上分辨率为0.5°×0.5°的格网扰动位T和重力梯度对角线分量Txx、Tyy、Tzz数据，并在扰动位中加入标准差为0.5 m2/s2的白噪声，在重力梯度各分量中加入标准差为8.0 mE的白噪声。基于球谐分析方法，分别采用格网扰动位T、径向重力梯度Tzz和重力梯度分量组合{Tzz－Txx－Tyy}进行重力场恢复计算。根据式(22)联合扰动位和重力梯度分量组合进行重力场恢复计算，并将联合求解模型与EIGEN-5C模型进行比较。图 1和图 2分别给出由扰动位、径向重力梯度、重力梯度分量组合、以及联合扰动位和重力梯度分量组合恢复重力场模型的阶误差RMS与累积大地水准面误差。
|
| 图 1 扰动位、重力梯度及其组合求解模型的阶误差RMS Fig. 1 Degree-error RMS solved from disturbing potential,gravity gradients and their combination |
|
| 图 2 扰动位、重力梯度及其组合解算的大地水准面累积误差 Fig. 2 Cumulative geoid height errors solved from disturbing potential,gravity gradients and their combination |
从图 1可以看出，扰动位T求解模型的位系数精度在低阶部分较高，在本文模拟条件下，大约在23阶以后则低于径向重力梯度Tzz求解模型的精度。重力梯度分量组合{Tzz－Txx－Tyy}比径向重力梯度Tzz求解模型的位系数精度更高，其原因是重力梯度分量组合相比单一分量包含了更丰富的重力场信息。从扰动位T和重力梯度分量组合{Tzz－Txx－Tyy}的联合求解模型阶误差RMS可知，联合模型在低阶部分接近于扰动位求解模型的精度，约在30阶以后密切接近于重力梯度分量组合求解模型的精度，它是介于两类数据求解模型之间的最优组合解。从图 2可以看出，联合求解模型相比径向重力梯度Tzz或重力梯度分量组合{Tzz－Txx－Tyy}求解模型的大地水准面精度在中低阶部分有了明显改善。
以上算例表明，扰动位和重力梯度数据在重力场反演中互为补充，本文推导的谱组合计算模型可以有效顾及各类数据的精度和频谱特性进行最优联合求解。
4.2 GOCE重力场解算利用2009-11-02—2010-01-02共61 d的GOCE实测数据进行重力场恢复计算。采用的数据包括：① L2几何法轨道数据，采样率为1 s，精度为2~3 cm；② L2局部指北坐标系(LNOF)下经过校准和时变改正的重力梯度数据，采样率为1 s；③ L1b重力梯度测量普通模式的加速度计数据和卫星姿态数据，采样率为1 s。其中，LNOF重力梯度数据是由梯度仪坐标系(GRF)下的重力梯度观测值经过坐标转换得到，坐标转换过程中利用高通滤波器处理有色噪声，并采用EIGEN-5C模型恢复低频信号。加速度计数据为仪器坐标系下的观测值，实际使用时需要结合卫星姿态数据将其转换到惯性系。以上数据的详细格式说明和坐标转换关系可参阅GOCE数据使用手册[17, 18]。
对几何法轨道数据采用“3倍标准差”准则剔除粗差后，基于能量守恒原理将几何法轨道和非保守力加速度计数据转化为沿轨扰动位，其中卫星速度采用7点牛顿数值微分公式由卫星位置计算。由于加速度计数据存在漂移，采用EIGEN-5C模型进行校准(每天校准1组参数)，具体方法参见文献[14]。图 3为2009-11-02校准前后得到的GOCE沿轨扰动位与EIGEN-5C模型计算值之差，可以看出对加速度计数据进行重新校准可有效控制扰动位数据的漂移误差。
|
| 图 3 校准前后的扰动位与EIGEN-5C模型计算值之差 Fig. 3 Difference of disturbing potential before and after calibrated compared with that of EIGEN-5C |
以EIGEN-5C模型计算的重力梯度数据为参考，对GOCE重力梯度数据进行粗差剔除，然后基于谱组合法联合GOCE沿轨扰动位和重力梯度数据进行重力场反演。本文采用二阶径向改正公式[19, 20]将沿轨扰动位和重力梯度数据归算至GOCE平均轨道球面(卫星高度为260 km)，采用配置法[19, 20]将平均轨道面上的扰动位和重力梯度数据进行格网化，并以EIGEN-5C模型计算值对两极半径约为6.5°的极空白区进行数据填充，最终形成全球0.5°×0.5°的规则格网数据。由于谱组合计算模型(式(20)或式(22))需要给出各类格网数据的精度信息，但在实际数据处理中很难估计经过归算与格网化处理后得到的格网数据精度。为此，本文将格网数据与高精度的EGM2008模型计算值进行比较，以此近似地估计格网扰动位和重力梯度数据的精度。表 1给出了GOCE平均轨道面上0.5°×0.5°的格网扰动位和格网重力梯度数据与EGM2008模型(取至2159阶次)计算值的差值统计，表中结果显示格网扰动位T、格网径向重力梯度Tzz和格网重力梯度分量组合{Tzz－Txx－Tyy}对应的均方根分别为0.623 m2/s2、8.138 mE和9.998 mE，本文采用该估计值进行谱组合定权计算。
| 格网数据 | 最大值 | 最小值 | 平均值 | 标准差 | 均方根 |
| T/(m2/s2) | 4.301 | -5.976 | -0.012 | 0.622 | 0.623 |
| Tzz/mE | 87.743 | -73.727 | 0.020 | 8.138 | 8.138 |
| {Tzz－Txx －Tyy}/mE |
164.397 | -137.048 | 0.040 | 9.998 | 9.998 |
图 4给出了利用GOCE沿轨扰动位T、径向重力梯度Tzz、重力梯度分量组合{Tzz－Txx－Tyy}、以及联合扰动位和重力梯度分量组合T+{Tzz－Txx－Tyy}恢复重力场模型的阶误差RMS。由信噪比分析可知，扰动位和径向重力梯度可恢复重力场模型的最大阶次分别约为100阶和176阶，而重力梯度分量组合可恢复重力场模型的最大阶次约为184阶。重力梯度分量组合相比径向重力梯度数据求解模型的精度有进一步提高，这与4.1节的数值模拟结果一致。采用谱组合法可以得到扰动位和重力梯度分量组合的最优联合求解模型，并且联合求解模型相比重力梯度分量组合求解模型的精度在低级部分(约30阶前)有进一步改善，体现了SST-hl观测在GOCE重力场恢复中对长波重力场信息的有益补充作用。
|
| 图 4 GOCE扰动位、重力梯度及其组合求解重力场模型的阶误差RMS Fig. 4 Degree-error RMS solved from disturbing potential,gravity gradients and their combination of GOCE |
将扰动位和径向重力梯度、以及扰动位和重力梯度分量组合的谱组合求解模型分别记为WHU_GOCE_SC01S和WHU_GOCE_SC02S，并与欧空局(ESA)首次发布的GOCE系列模型(时域解GO_CONS_GCF_2_TIM_R1、空域解GO_CONS_GCF_2_SPW_R1和直接解GO_CONS_GCF_2_DIR_R1，约71 d GOCE观测数据求解)进行比较，图 5为上述各模型相比EGM2008模型的阶误差RMS。
|
| 图 5 谱组合求解模型和GOCE系列模型相比EGM2008模型的阶误差RMS Fig. 5 Degree-error RMS of spectral combination computing models and three GOCE models compared with EGM2008 |
从图 5可以看出：WHU_GOCE_SC01S和WHU_GOCE_SC02S模型在约90阶前优于GOCE时域解的精度，在约30阶至120阶与GOCE空域解的精度非常接近；WHU_GOCE_SC01S和WHU_GOCE_SC02S模型与公布的GOCE系列模型在90阶至120阶具有一致性，但在120阶以后其精度低于GOCE系列模型。需要说明的是，GOCE时域解在约90阶以下精度较低是与其求解过程中没有采用任何先验重力场模型信息有关，GOCE空域解在30阶以下精度较高是由于其求解过程中采用EGM2008模型作为约束进行了“移去-恢复”处理，而公布的GOCE系列模型在高阶部分精度较高是由于它们在求解过程中做了正则化处理[2]。从图 5还可以看出，WHU_GOCE_SC02S模型精度优于WHU_GOCE_SC01S模型，其原因是前者采用的重力梯度分量组合包含了更为丰富的重力场信息，进而有利于重力场反演精度的提高。
为了进一步评价谱组合求解模型的精度与可靠性，取上述各模型前180阶位系数分别计算全球1°×1°格网大地水准面高，表 2给出了谱组合求解模型、GOCE系列模型与EGM2008模型比较得到的大地水准面差值统计结果。可以看出：WHU_GOCE_SC01S和WHU_GOCE_SC02S模型的大地水准面高度差值均方根分别为0.284 m和0.249 m，明显优于GOCE时域解的精度，而与GOCE空域解的精度更为接近；GOCE直接解的大地水准面高度差值均方根为0.099 m，明显优于其它比较模型的精度，其原因是直接解的求解过程更为严密，并且解算中采用了精度更高的简化动力学轨道数据和先验重力场模型信息[2]。
| m | |||||
| 重力场模型(阶次) | 最大值 | 最小值 | 平均值 | 标准差 | 均方根 |
| GO_CONS_GCF_ 2_TIM_R1(180) |
3.122 | -6.711 | -0.054 | 0.573 | 0.575 |
| GO_CONS_GCF_ 2_SPW_R1 (180) |
3.042 | -2.611 | 0.002 | 0.171 | 0.171 |
| GO_CONS_GCF_ 2_DIR_R1 (180) |
2.406 | -1.876 | -0.001 | 0.099 | 0.099 |
| WHU_GOCE_ SC01S(180) |
2.887 | -2.705 | -0.005 | 0.284 | 0.284 |
| WHU_GOCE_ SC02S(180) |
2.829 | -2.763 | -0.004 | 0.249 | 0.249 |
研究了联合高低卫-卫跟踪和卫星重力梯度数据反演地球重力场的谱组合法，推导并建立卫星轨道面扰动位T和径向重力梯度Tzz、以及扰动位T和重力梯度分量组合{Tzz－Txx－Tyy}的谱组合计算模型。数值模拟结果和GOCE实测数据解算结果表明，谱组合计算模型可以有效顾及各类数据的精度和频谱特性进行最优联合求解，验证谱组合法在卫星重力数据联合求解中的有效性。
基于球谐分析方法建立的谱组合计算模型具有表达简洁、物理意义明显和计算量小等特点，可用于GOCE重力场模型的快速求解。但应用球谐分析方法不可避免地存在积分离散化误差，该误差可通过提高格网数据的分辨率进行削弱。本文采用经验方法对各类格网数据的精度进行估计会引入近似误差，因此如何精确估计球面格网数据的精度，将是后续研究中需要着重考虑的问题。此外，如何将非对角线重力梯度分量有效地纳入谱组合计算模型，也是下一步研究中需要完善的问题。
致 谢：宁津生院士是我国著名大地测量学家，为我国测绘事业发展和人才培养做出了重要贡献。值此宁津生院士80华诞之际，特撰写此文以表达对他的崇高敬意，并感谢他对作者多年的培养。同时，感谢欧空局(ESA)提供了本文计算所需的GOCE卫星精密轨道和重力梯度数据。| [1] | DRINKWATER M, FLOBERGHAGEN R, HAAGMANS R, et al. GOCE: ESA’s first Earth Explorer core mission[J]. Space Science Reviews, 2003, 108(1): 419-432. |
| [2] | PAIL R, BRUINSMA S, MIGLIACCIO F, et al. First GOCE Gravity Field Models Derived by Three Different Approaches[J]. Journal of Geodesy, 2011, 85(11): 819-843. |
| [3] | PAIL R, PLANK G. GOCE Gravity Field Processing Strategy[J]. Studia Geophysica et Geodaetica, 2004, 48(2): 289-309. |
| [4] | PAIL R, GOIGINGER H, MAYRHOFER R, et al. GOCE Gravity Field Model Derived from Orbit and Gradiometry Data Applying the Time-wise Method[C]//Proceedings of the ESA Living Planet Symposium. Bergen:[s.n.], 2010. |
| [5] | REGUZZONI M, TSELFES N. Optimal Multi-step Collocation: Application to the Space-wise Approach for GOCE Data Analysis[J]. Journal of Geodesy, 2009, 83(1): 13-29. |
| [6] | MIGLIACCIO F, REGUZZONI M, SANSò F, et al. GOCE Data Analysis: the Space-wise Approach and the First Space-wise Gravity Field Model[C]//Proceedings of the ESA Living Planet Symposium. Bergen :[s.n.], 2010. |
| [7] | BRUINSMA S, MARTY J, BALMINO G, et al. GOCE Gravity Field Recovery by Means of the Direct Numerical Method[C]//Proceedings of the ESA Living Planet Symposium.Bergen:[s.n.], 2010. |
| [8] | KOCH K R, KUSCHE J. Regularization of Geopotential Determination form Satellite Data by Variance Components[J]. Journal of Geodesy, 2002, 76(5): 259-268. |
| [9] | BROCKMANN J M, KARGOLL B, KRASBUTTER I, et al. GOCE Data Analysis: From Calibrated Measurements to the Global Earth Gravity Field[C]//Proceedings of System Earth via Geodetic-Geophysical Space Techniques, Advanced Technologies in Earth Sciences.[S.l.] :Springer-verlag,2010:213-229. |
| [10] | SJBERG L. Least Squares Combination of Satellite and Terrestrial Data in Physical Geodesy[J]. Ann. Géophys, 1981, 37: 25-30. |
| [11] | SHI Pan. On the Improvement of Gravity Field Model using Regional Gravity Data[J]. Acta Geodaetica et Cartographica Sinica, 1994, 23(4): 276-281.(石磐. 利用局部重力数据改进重力场模型[J]. 测绘学报, 1994, 23(4): 276-281.) |
| [12] | WU Xiaoping, LU Zhonglian. Optimal Spectral Combination Solution with Integral Kernel for the Downward Continuation of Spaceborne Gravity Gradiometrical Data[J]. Acta Geodaetica et Cartographica Sinica, 1992, 21(2): 123-133.(吴晓平, 陆仲连. 卫星重力梯度向下沿拓的最佳积分核谱组合解[J]. 测绘学报, 1992, 21(2): 123-133.) |
| [13] | KERN M, SCHWARZ K P, SNEEUW N. A Study on the Combination of Satellite, Airborne, and Terrestrial Gravity Data[J]. Journal of Geodesy, 2003, 77(3-4): 217-225. |
| [14] | XU Tianhe, YANG Yuanxi. CHAMP Gravity Field Recovery using Energy Conservation Method[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(1): 1-6.(徐天河, 杨元喜. 基于能量守恒法恢复CHAMP重力场模型[J]. 测绘学报, 2005, 34(1): 1-6.) |
| [15] | SHI Pan. Combined Determination of the Earth’s Disturbing Potential[J]. Acta Geodaetica et Cartographica Sinica, 1984, 13(4): 241-248.(石磐. 扰动位的综合确定[J]. 测绘学报, 1984, 13(4): 241-248.) |
| [16] | XU Xi, ZHU Jianjun. Relative Accuracy Estimation for Determining Regional Gravimetric Geoid[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(5): 383-390.(许曦, 朱建军. 区域重力大地水准面确定的相对精度估计[J]. 测绘学报, 2009, 38(5): 383-390.) |
| [17] | SERCO/DATAMAT Consortium. GOCE HPF: GOCE L1B Products User Handbook[R]. Noordwijk :European Space Agency, 2008. |
| [18] | SERCO/DATAMAT Consortium. GOCE HPF: GOCE Level 2 Product Data Handbook[R]. Noordwijk: European Space Agency, 2010. |
| [19] | XU Tianhe, HE Kaifei, WU Xianbing. Comparison of Time-Wise Approach and Space-Wise Approach for CHAMP Gravity Field Recovery[J]. Progress in Geophysics, 2009, 24(2): 456-461.(徐天河, 贺凯飞, 吴显兵. CHAMP重力场恢复时域法和空域法比较研究[J]. 地球物理学进展, 2009, 24(2): 456-461.) |
| [20] | ZHONG Bo, LIU Hualiang, LUO Zhicai, et al. Reduciton and Gridded Processing of Satellite Gravity Gradient Data[J]. Journal of Geodesy and Geodynamics, 2011, 31(3): 79-84.(钟波, 刘华亮, 罗志才, 等. 卫星重力梯度数据的归算与格网化处理[J]. 大地测量与地球动力学, 2011, 31(3): 79-84.) |