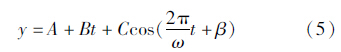2. 国家测绘地理信息局 卫星测绘应用中心,北京 100830
2. Satellite Surveying and Mapping Application Center, National Administration of Surveying, Mapping and Geoinformation, Beijing 100830, China
1 引 言
海平面的监测手段主要有验潮站观测、卫星测高、海洋温盐测量等,利用这些观测数据已得到了许多海平面变化方面的研究成果。20世纪90年代以前,对于海平面变化的监测主要依靠离散的验潮站观测数据,有些验潮站的观测时间甚至长达100多年,为海平面变化的研究提供了长期的观测资料。文献[1]选取超过50年的验潮站数据,估计到20世纪海平面的上升速度为(1.84±0.35) mm/a;文献[2]估计了1950—2000年间海平面上升速度为(1.7±0.4) mm/a,而文献[3]得到的这一时间段内的结果为(1.8±0.3) mm/a,文献[4]估计了1900—2009年间海平面的上升速度为(1.7±0.2) mm/a,而1961—2009年间海平面的上升速度为(1.9±0.4) mm/a,这些研究结果均显示了全球海平面在逐年上升。20世纪70年代末出现的卫星测高技术为研究全球海平面变化提供了非常有效的方法,文献[5]利用1993—2003年的TOPEX/Poseidon和Jason-1卫星测高数据估算的海平面上升速度为(3.1±0.7) mm/a。1992年底到2011年6月间,综合TOPEX/Poseidon、Jason-1、Jason-2等多种卫星测高数据,并扣除季节变化,不同机构估算的海平面上升结果也比较接近,文献[6]给出的结果为(3.2±0.4) mm/a,法国AVISO(Archiving,Validation and Interpretation of Satellite Oceanographic Data)得到的结果为3.2±0.6 mm/a,NOAA(National Oceanic and Atmospheric Administration)得到的结果为3.2±0.4 mm/a(考虑了冰后回弹的影响)。可以看出,卫星测高数据估算的海平面上升速度比验潮站数据得到的结果略大。导致海平面上升的主要因素可以归结为海水膨胀、大陆冰川和冰盖的融化、以及格陵兰和南极冰质量亏损等。海平面变化的比容效应是由于海水温度和盐度的变化而引起的海水膨胀或收缩,但海水的总质量不发生变化。文献[7]利用1995—2003年间的观测数据得到的海水热膨胀引起的海平面上升速度为0.4 mm/a,而根据卫星观测数据得到的海平面上升速度为1.2 mm/a。GRACE卫星提供的时变重力场数据为反演海水质量变化提供了新途径,文献[8]计算结果表明经过500 km的平滑,GRACE能探测2.4 cm等效水高的海平面变化。
Argo海洋观测网可以持续地获取大部分海洋的海水温度和盐度数据,为比容海平面变化研究提供了丰富的数据。文献[9]综合利用Jason-1、GRACE和Argo数据研究了比容海平面变化,估计得到2003—2008年海平面上升速度为(2.5±0.4) mm/a,其中由GRACE估算的海水质量变化引起的海平面变化约为1.99 mm/a。文献[10]利用2002—2009年间的卫星测高、Argo浮标、GRACE等数据研究了海平面的不同分量,即由卫星测高得到的总海平面变化、比容海平面变化以及由海水质量变化引起的海平面变化等,并研究了这些量的区域变化以及年际变化。文献[11]利用EOF分析了TOPEX/Poseidon和ERS-2得到的海面高异常时间序列,文献[12]等利用Jason-1和GRACE数据分析了比容海平面变化。本文根据2004-01—2010-12间的Argo浮标观测数据,估算了全球比容海平面变化,并利用相同时间段内的GRACE月重力场模型估计了由于海水质量变化所引起的海平面变化,并将这两种数据得到的海平面变化与卫星测高数据得到的海平面变化进行了比较。 2 Argo浮标数据计算比容海平面变化 2.1 温盐数据计算比容海平面变化的方法
比容海平面变化是由海水的温度和盐度的变化而引起的,海洋中一点(φ,λ)处的比容海平面异常可通过对垂直方向上的海水密度变化进行积分得到[13]
式中,Δη为比容海平面异常;(φ,λ)分别为点的纬度和经度;ρ0为海水平均密度,通常取ρ0=1028 kg/m3;z为点的深度,通常以平均海面起算,向下为正;T、S分别为温度和盐度;T、S分别为平均温度和平均盐度;ρ(φ,λ,z,T,S)和ρ(φ,λ,z,T,S)分别为积分点的海水密度和平均海水密度;h为积分的最大深度。随着深度的增加,海水温盐的变化减小甚至不发生变化,因此采用式(1)计算时,通常仅积分至某一深度即可。文献[14]的实验结果表明深度大于1000 m的海水密度变化对比容海平面变化影响较小,因此,本文选取1000 m作为最大积分深度。
海水的密度可由海水温度、盐度、压力计算得到
式中,P为压力;T、S分别为海水温度、盐度;ρ(T,S,0)为标准海水密度;K(T,S,P)为海水割线模量;计算公式如下:式中,b0~b3、c0~c3、d0以及A和B等分别为常量,详见文献[15]。 2.2 Argo浮标数据计算比容海平面变化
美国等国家的大气、海洋科学家于1998年提出了“Argo(array for real-time geostrophic oceanography)全球海洋观测网”计划。该计划设计2000—2004年在全球大洋以3°×3°的分辨率布设约3000个Argo浮标,但直至2007年才基本达到了设计的密度[16]。Argo浮标又称自持式剖面自动循环探测仪或中性剖面自动探测漂流浮标,是采用拉格朗日环流法对海洋次表层温度、盐度进行剖面测量的探测器。每个浮标的设计寿命为3~5年,仪器在水中处于自由漂流状态,布放后自动潜入2000 m深处的等密度层,随海流保持中性漂浮,到达预定时间仪器自动上升至水面,在攀升过程进行温度、盐度剖面测量,到达水面后将采集的资料传送给数据中心。Argo浮标主要分布在65°S~65°N,我国自从2001年正式加入该计划以来,在太平洋、印度洋等海域累计投放114个Argo浮标,目前仍有65个在正常工作,图 1显示了2004-01和2010-12 Argo浮标的分布情况。

|
| 图 1 2004-01和2010-12 Argo浮标分布图 Fig. 1 Distribution of Argo floats in Jan.2004 and Dec.2010 |
采用日本海洋科技中心(Japan Agency for Marine-Earth Science and Technology,JAMSTEC)提供的2004-01—2010-12间1°×1°的Argo格网数据。该数据集沿深度0-2000 m分为25层,如表 1所示。该数据集主要以Argo数据为主,由于在Argo全球观测网建立初期,Argo浮标数量较少,所以该数据集还采用了部分三角跨海洋浮标系统(triangle trans-ocean buoy network,TRITON)的数据和CTD(conductivity-temperature-depth profilers)数据。
| 层 | 深度/m | 层 | 深度/m |
| 1 | 10 | 14 | 600 |
| 2 | 20 | 15 | 700 |
| 3 | 30 | 16 | 800 |
| 4 | 50 | 17 | 900 |
| 5 | 75 | 18 | 1000 |
| 6 | 100 | 19 | 1100 |
| 7 | 125 | 20 | 1200 |
| 8 | 150 | 21 | 1300 |
| 9 | 200 | 22 | 1400 |
| 10 | 250 | 23 | 1500 |
| 11 | 300 | 24 | 1750 |
| 12 | 400 | 25 | 2000 |
| 13 | 500 |
利用Argo数据根据式(1)计算了2004-01—2010-12间65°S~65°N内的月比容海平面变化,结果如图 2(a)、2(c)所示。

|
| 图 2 Argo浮标数据和WOA05数据集得到的比容海平面变化 Fig. 2 Comparison of steric sea level derived from Argo floats and that from WOA05 |
为了与Argo浮标数据的计算结果进行比较,采用了WOA05(World Ocean Atlas 2005)海洋数据集。WOA05是由美国海洋数据中心(NODC)发布的海洋客观分析气候性数据集,包含海洋现场温度、盐度、溶解氧含量等海洋学参数。WOA05数据集包含月平均、季度平均和年平均等3种数据,空间分辨率分为1°×1°和5°×5° 2种,WOA05数据集反映的是海洋要素的多年平均分布,不含年际变化,本文采用1°×1°的月平均和年平均的温度和盐度数据。
利用WOA05数据集计算了12个月的比容海平面变化,如图 2(b)、2(d)所示(仅列出2007-03和2007-10的结果)。从图 2可以看出全球比容海平面变化量级在-10 cm~10 cm,其中太平洋的西北部、太平洋中南部、印度洋东北部、大西洋的西北部和西南部等区域内变化幅度较大,利用Argo浮标数据推算的结果与WOA05数据集计算的结果较为接近,特别是在比容海平面变化相对较大的区域内。
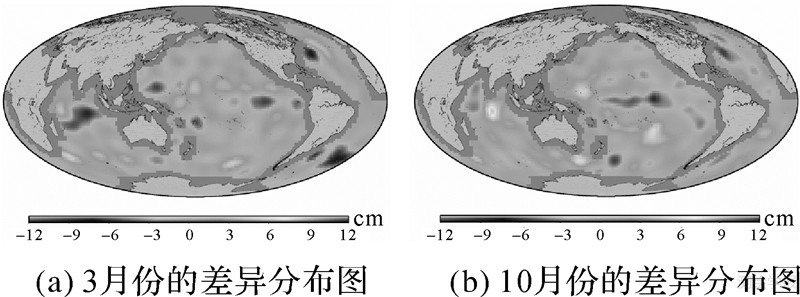
图 3显示了3月和10月Argo浮标数据的计算结果与WOA05数据集得到的结果之间的差异,统计得出90%的格网上两者差异在-3 cm~3 cm内。造成二者差异的原因可能是由于WOA05数据是多年的平均值,不含年际变化。
|
| 图 3 Argo数据与WOA05得到的比容海平面异常的差异 Fig. 3 The difference of steric sea level anomaly derived from Argo and WOA05 |
将Argo浮标数据计算的月比容海平面异常,按cos φ进行加权平均得到月平均比容海平面变化,如图 4所示。

|
| 图 4 全球平均比容海平面变化 Fig. 4 Global mean steric sea level change |
对全球月平均比容海平面变化的时间序列进行最小二乘拟合
式中,y为比容海平面变化;A为常数项;B为长期趋势项;t为时间;C为振幅;ω为周期;β为相位。求得线性项B为(0.63±0.45) mm/a,振幅为(4.3±0.62) mm,相位为(103±5)°。由于只采用了2004-01—2010-12间的数据,估算的线性项的可靠性还不高,但随着Argo数据的不断累积,确定全球比容海平面变化的精度将更加准确。表 2比较了本文计算结果与Llovel(2010年)的结果,可以看出,本文的计算结果与利用SCRIPPS中心的Argo数据所得结果吻合较好。由Llovel的结果可以看出,利用不同中心的Argo数据的计算结果之间存在一定的差异,可能与不同中心Argo数据的编辑准则和处理方法不同有关。
| 中心 | 振幅 /mm |
相位 /(°) |
趋势 /(mm/a) |
时间 | |
| Llovel | SCRIPPS | 4.5±0.3 | 100±2 | 0.35±0.2 | 2004-01—2009-04 |
| IPRC | 4.7±0.4 | 98±3 | 0.19±0.13 | 2005-01—2009-04 | |
| CLS | 3.5±0.34 | 95±2 | 0.9±0.1 | 2004-01—2009-04 | |
| 本文 | JAMSTEC | 4.3±0.62 | 103±5 | 0.63±0.45 | 2004-01—2010-12 |
AVISO中心提供的海面高异常格网数据,融合了T/P、Jason、ERS、Envisat等多种卫星测高数据,采用1993—1999年间的平均海面作为参考。选用2004-01—2010-12间空间分辨率为0.25°×0.25°,时间分辨率为7 d的海面高异常格网数据,估算了海平面变化,结果如图 5所示(仅列出部分月份)。

|
| 图 5 卫星测高计算的海平面异常 Fig. 5 Sea level anomaly derived from satellite altimetry |
对海平面变化按cos φ进行全球加权平均,得到全球海平面变化,结果如图 6所示。利用最小二乘拟合得到海平面变化的长期趋势为(2.22±0.71) mm/a。在计算海平面变化长期变化趋势时应顾及冰川均衡调整(glacial isostatic adjustment,GIA)的影响。GIA在较长时间尺度上会使海盆体积增大,造成全球海平面以约0.3 mm/a的速度下降[17]。经过此项改正后,卫星测高得到的总体海平面长期变化趋势为(2.52±0.71) mm/a。

|
| 图 6 卫星测高估算的全球海平面变化 Fig. 6 Global sea level change from satellite altimetry |
由GRACE时变地球重力场球谐系数残差(ΔClm(t),ΔSlm(t))计算质量变化(以等效水高表示)的公式为[18]
式中,aE为地球平均半径;ρE为地球平均密度(5517 kg/m3);ρW为淡水密度(1000 kg/m3);N为重力场模型的最高阶;kl为负荷勒夫数;Wl为空间平均函数;Plm(sin Φ)是完全正则化缔合勒让德函数。利用GRACE数据反演海水质量变化时,选用文献[19]推荐的地球质心改正模型顾及1阶项的影响,并采用卫星激光测距(SLR)得到的C20项系数[20]来替代GRACE重力场模型的C20项,反演过程中还采用了去相关滤波方法[21]。 3.2.2 GRACE数据反演的海水质量变化结果
选用2004-01—2010-12间美国德克萨斯大学空间研究中心(UTCSR)发布的Level-2 RL04版本的GRACE月重力场模型,最高阶为60,反演得到的海水质量变化如图 7所示(仅列出部分月份结果)。

|
| 图 7 GRACE反演得到的海水质量变化 Fig. 7 The oceanic mass change derived from GRACE |
对每个月的海水质量变化按cos φ进行全球加权平均,得到全球平均海水质量变化,如图 8所示。

|
| 图 8 GRACE计算的全球平均海水质量变化 Fig. 8 Global mean oceanic mass change derived from GRACE |
利用最小二乘拟合得到由海水质量变化引起的海平面长期变化趋势为(-0.16±0.13) mm/a,年周期项的振幅为(8.3±0.34) mm,初相为(266±9)°。表 3为本文计算结果与其他学者计算结果的比较(未经GIA改正)。
GIA改正对海水质量的长期变化趋势有较大的影响,选取不同的GIA改正模型,其对海水质量长期变化趋势的影响也不同,约为1~2 mm/a,如文献[22]采用1 mm/a,文献[23]采用1.7 mm/a;文献[24]建议GIA改正值采用+2.0 mm/a,关于GIA模型的比较,可参阅文献[27]。本文取+2.0 mm/a对GRACE反演的海水质量变化趋势进行改正后为(1.84±0.13) mm/a。
由卫星测高、GRACE及Argo浮标数据计算结果,可以得出总海平面及各分量的长期变化趋势,如表 4所示。可以看出,2004-01-2010-12间总海平面长期变化趋势为(2.52±0.71) mm/a,较1993—2003年间3.1 mm/a的上升速度有所减慢,其中海水质量变化引起的海平面变化占总海平面变化的73%左右,已成为影响海平面变化的主要因素,而比容海平面变化对总海平面变化的贡献则较小。
| 数据源 | 变化趋势 /(mm/a) |
时间 | |
| 总体海平面变化 | 卫星测高 | 2.52±0.71 | 2004-01—2010-12 |
| 海水质量变化 | GRACE | 1.84±0.13 | 2004-01—2010-12 |
| 比容海平面变化 | Argo | 0.63±0.45 | 2004-01—2010-12 |
卫星测高能够精确测量总海平面变化,而利用GRACE时变重力场数据能够反演得到因海水质量变化引起的海平面变化,二者之差即可得到比容海平面变化。
联合上述2种数据计算比容海平面变化时,应考虑两种数据处理过程的一致性,采用高斯平滑消除GRACE重力场模型的高阶项误差,为了保证数据处理过程的一致性,应对卫星测高数据进行类似处理。采用Chambers(2006b)的处理策略,基本过程为:首先对卫星测高得到的海面高异常格网数据进行球谐展开至60阶,然后采用半径为500 km的高斯滤波进行平滑处理,最后再利用球谐综合恢复格网数据,联合以上2种数据得到的比容海平面变化如图 9(a)、9(c)所示。

|
| 图 9 Argo与GRACE和卫星测高的比容海平面变化比较 Fig. 9 The comparison of steric sea level change from Argo and that from GRACE and satellite altimetry |
Argo浮标数据计算得到的比容海平面变化,如图 9(b)、9(d)所示,比较图 9(a)与9(b),以及9(c)与9(d),可以看出联合卫星测高与GRACE得到的比容海平面变化的主要空间分布特征与Argo浮标数据计算的结果较为一致,图 9(a)、9(b)中在太平洋东部海平面变化均呈现明显的下降,图 9(c)、9(d)在太平洋中部都呈现较大的上升趋势。利用GRACE时变重力场数据仅能探测厘米级精度[8]的海水质量变化,因此GRACE卫星较低的反演精度、卫星测高的测量误差以及两者联合求解比容海平面变化过程引入的误差都会使得联合卫星测高、GRACE得到的比容海平面变化与Argo数据的结果存在差异,造成这种差异的部分原因还可能是由于Argo浮标分布的不均匀。如何更好地融合卫星测高、GRACE数据、以及ARGO浮标等数据以得到更高精度的海平面变化还有待进一步深入研究。 5 结束语
利用2004-01—2010-12间的Argo浮标温度、盐度数据,计算得到65°S~65°N间的全球比容海平面变化速度为(0.63±0.45) mm/a,与Llovel根据2002—2009年间的数据所得的计算结果较为一致。利用卫星测高数据得到的该时间段内的总海平面变化速度为(2.52±0.71) mm/a,GRACE地球重力场模型反演得到的由海水质量变化而引起的海平面变化速度为(1.84±0.13) mm/a,比容海平面变化加上海水质量变化引起的海平面变化速度与卫星测高得到的海平面变化速度吻合较好,由结果可以看出,近年来海平面上升趋势较1993—2003年间有所减缓。关于GIA的影响,还有待进一步深入研究。
| [1] | DOUGLAS B,KEARNEY M,LEATHERMAN S.Sea Level Rise[M].New York: Academic Press,2001: 37-64. |
| [2] | HOLGATE S J,WOODWORTH P L.Evidence for Enhanced Coastal Sea Level Rise During the 1990s[J].Geophysical Research Letter,2004,31(L07305):1-4. |
| [3] | CHURCH J,WHITE N,COLEMAN R,et al.Estimates of the Regional Distribution of Sea Level Rise over the 1950 to 2000 Period[J].Journal of Climate,2004,17(13):2609-2625. |
| [4] | CHURCH J,WHITE N.Sea-level Rise from the Late 19th to the Early 21st Century[J].Survey in Geophysics,2011,32(4-5):585-602. |
| [5] | CAZENAVE A,NEREM R S.Present-day Sea Level Change:Observations and Causes[J].Reviews of Geophysics,2004,42(GR3001):1-20. |
| [6] | CU Sea Level Research Group. 2012_Rel3: Global Mean Sea Level Time Series: Seasonal Signals Removed[EB/OL]. Boulder: University of Colorado, (2012-06-28). http://sealevel. colorado.edu/. |
| [7] | ANTONOV J,LEVITUS S,BOYER T.Thermosteric Sea Level Rise,1955-2003[J].Geophysical Reseach Letters,2005,32(L12602):1-4. |
| [8] | CHAMBERS D.Evaluation of New GRACE Time-Variable Gravity Data over the Ocean[J].Geophysical Reseach Letters,2006,33(L17603),doi:10.1029/2006GL027296. |
| [9] | CAZENAVE A,DOMINH K,GUINEHUT S,et al.Sea Level Budget over 2003—2008:a Reevaluation from GRACE Space Gravimetry,Satellite Altimetry and Argo[J].Global and Planetary Change,2009,65(1-2):83-88. |
| [10] | LLOVEL W,GUINEHUT S,CAZENAVE A.Regional and Interannual Variability in Sea Level over 2002-2009 Based on Satellite Altimetry,Argo Float Data and GRACE Ocean Mass[J].Ocean Dynamic,2010,60(5):1193-1204. |
| [11] | WEN Hanjiang,ZHANG Chuanyin.EOF Analysis of Sea Level Anomaly Time Series Derived from ERS-2 and TOPEX Altimeter Data[J].Geomatics and Information Science of Wuhan University,2006,31(3):221-223.(文汉江,章传银.由ERS-2和TOPEX卫星测高数据推算的海面高异常的主成分分析[J].武汉大学学报:信息科学版,2006,31(3):221-223.) |
| [12] | JIANG Tao,LI Jiancheng,WANG Zhengtao,et al.Global Sea Level Variations from Combined Jason-1 and GRACE Data[J].Acta Geodaeticaet Cartograhpica Sinica,2010,39(2):135-140.(蒋涛,李建成,王正涛,等.联合Jason-1与GRACE卫星数据研究全球海平面变化[J].测绘学报,2010,39(2):135-140.) |
| [13] | CHEN J,WILSON C,TAPLEY B,et al.Seasonal Global Mean Sea Level Change from Satellite Altimeter,GRACE and Geophysical Models[J].Journal of Geodesy,2005,79(9):532-539. |
| [14] | DHOMPS A, GUINEHUT S, TRANON P Y, et al. A Global Comparison of Argo and Satellite Altimetry Observations[J]. Ocean Science, 2011, 7(2): 175-183. |
| [15] | FOFONOFF N,MILLARD R.Algorithms for Computation of Fundamental Properties of Seawater[J].New York: UNESCO,1983: 15-19. |
| [16] | XU Jianping,ZHU Bokang. Introduction to Array for Real-Time Geostrophic Oceanography[J].Ocean Technology,2001,20(2):15-17.(许建平,朱伯康.Argo全球海洋观测网与我国海洋监测技术的发展[J].海洋技术,2001,20(2):15-17.) |
| [17] | DOUGLAS B,PELTIER W.The Puzzle of Global Sea-Level Rise[J].Physica Today,2002,55(3):35-40. |
| [18] | CHAMBERS D P.Observing Seasonal Steric Sea Level Variations with GRACE and Satellite Altimetry[J].Journal of Geophysical Research,2006,111(C03010): 1-13. |
| [19] | CHEN J,WILSON C,EANES R,et al.Geophysical Interpretation of Observed Geocenter Variations[J].Journal of Geophysical Research,1999,104(B2):2683-2690. |
| [20] | CHENG M,TAPLEY B.Variations in the Earth’s Oblateness During the Past 28 Years[J].Journal of Geophysical Research,2004,109(B3):3406-3414. |
| [21] | SWENSON S, WAHR J. Post-processing Removal of Correlated Errors in GRACE Data[J].Geophysical Research Letters,2006,33(L08402):1-4. |
| [22] | WILLIS J,CHAMBERS D,NEREM R.Assessing the Globally Averaged Sea Level Budget on Seasonal to Interannual Timescales[J].Journal of Geophysical Research,2008,113(C060015):1-9. |
| [23] | LOMBARD A,GARCIA D,RAMILLIEN G,et al.Estimation of Steric Sea Level Variations from Combined GRACE and Jason-1 Data[J].Earth and Planetary Science Letters,2007,254(1-2):194-202. |
| [24] | PELTIER W.Global Glacial Isostasy and the Surface of the Ice-Age Earth:The ICE-5G(VM2) Model and GRACE[J].Annual Review of Earth Planetary Science,2004,32(1):111-149. |
| [25] | CHAMBERS D,WAHR J,NEREM R.Preliminary Observations of Global Ocean Mass Variations with GRACE[J].Geophysical Research Letters,2004,31(13): 1-4. |
| [26] | JIN Taoyong,LI Jiancheng,WANG Zhengtao,et al. Global Ocean Mass Variation in Recent Four Years and Its Spatial and Temporal Characteristics[J].Chinese Journal Geophysics, 2010,53(1):49-56,(金涛勇,李建成,王正涛,等.近四年全球海水质量变化及其时空特征分析[J].地球物理学报,2010,53(1):49-56. |
| [27] | GUO Junyi, HUANG Zhengwei, SHUM C K, et al. Comparisons among Contemporary Glacial Isostatic Adjustment Models[J]. Journal of Geodynamies,2012, 58(4):1-9. |