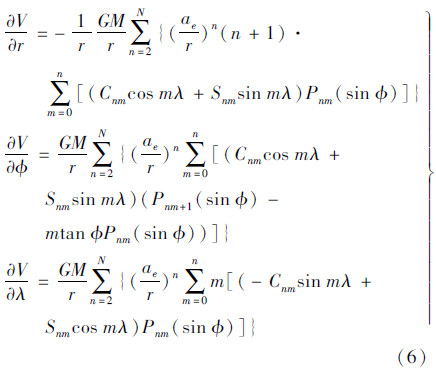2.武汉大学测绘学院,湖北武汉 430079
2.School of Geodesy and Geomatics,Wuhan University,Wuhan 430079,China
1 引言
基于CHAMP (challenging minisatellite payload)和GRACE (gravity recovery and climate experiment)卫星计划,人类以前所未有的精度和分辨率获取了整体地球的重力场稳态及其随时间变化的中长波信息[1, 2, 3]。但因高精度重力卫星平台复杂度高,星载加速度计(ACC),K波段测距仪(KBR)等关键有效载荷制造、测试和安装十分困难等技术原因,类似CHAMP和GRACE的重力卫星探测计划需要较长的研发周期且耗费高昂,难以广泛实施。鉴于此,GRACE卫星的任务期也由原计划的5年延至10年,尽量缩短后续计划和当前计划的空白期。另一方面,多用途的低成本LEO卫星和星座迅速发展为相关行业提供了很好的卫星平台,广泛应用于遥感、气象、空间探测等领域。这些LEO卫星和星座的共同特点是将高精度星载GPS接收机作为标准载荷进行LEO卫星平台精密轨道跟踪。2006-04-14美国和中国台湾省联合研制的COSMIC卫星星座[2]在美国Vandenberg空军基地以“一箭六星”的方式成功发射。该卫星计划的空间部分由6颗倾角为71°,初始轨道高度为400km的COSMIC卫星组成。卫星轨道在系统运行过程中逐步上升,发射一年后稳定运行于800km高度。每颗COSMIC卫星均搭载了3台主要有效荷载:GPS掩星(定轨)观测接收机、微型电离层成像仪和三波段信标发射机。其主要任务是通过对掩星观测数据的处理,由CDAAC(COSMIC Data Analysis and Archive Center)和TACC(Taiwan Analysis Center for COSMIC)提供包括地表至40km高度的湿度、温度、气压、各大气参数的垂直廓线以及上部大气层的电子密度信息的数据产品[4, 5, 6]。同时,该卫星计划为研究地球重力场提供了一种新的模式[7]。相对其他重力卫星系统,COSMIC在某些方面具有显著优势:COSMIC没有搭载制造和安装难度极高的星载加速度计和星载K波段测距系统,成本较低;卫星质量较轻(单颗 < 70kg)可一箭多星发射;体积小外形相对简单易于大气阻力和光压摄动的精确模型化;卫星数多达6颗(CHAMP为1颗,GRACE为2颗),完成一次全球覆盖的时间短且覆盖密度更大。这些优点使其在获取全球时变重力场信息方面具有一定优势。而且伴随更多的LEO卫星和星座计划的发射,所构成的具有GPS定轨能力的LEO星群将以更高的空间分辨率和时间分辨率覆盖全球,并可以作为GRACE和其后续计划之间全球时变重力场探测数据间断期的补充。
目前LEO星群反演地球重力场的方法主要有经典的动力学法[8, 9, 10],基于能量守恒原理的能量法[11]等。由于低成本LEO卫星未搭载加速度计,非保守力的模型化精度将直接影响重力场的反演精度,所以作者引入在重力网数据处理[12]和卫星测高数据处理[13, 14]领域经常使用的“交叠点”概念,提出一种星-星对之间构成所谓的交叠点,针对交叠点处两弧段非保守力之差更易模型化,且精度更高的特点,在交叠点处直接计算加速度差,进而确定重力场时变信息的方法——“交叠点法”。文献[15]对交叠点法应用于低成本COSMIC星座地球重力场恢复的有效覆盖特性进行了分析[15]。分析结果表明低成本LEO星群可以较高的时间分辨率很好地覆盖全球区域,但是对卫星的定轨精度要求较高,需要1cm级的定轨精度。在此基础上,本文开展利用交叠点法反演地球重力场低阶带谐项变化的研究,主要内容包括计算模型、数据的覆盖特性分析、LEO卫星的轨道精度分析和模拟数据计算验证。 2 计算低阶带谐项变化的交叠点法
本文交叠点的定义与卫星测高学相同。如图 1所示,LEO星群的任两颗卫星形成的降弧段(0号)和升弧段(1号)的交叠点。交叠点在0号弧段上的对应位置为A,对应时刻为t0,在1号弧段上的对应位置为B,对应时刻为t1。令A和B点处加速度分别为aA和aB。卫星飞越0弧段和1弧段的时间差即为所求重力场变化的时间跨度。因两卫星在飞跃交叠点位置时高度不一,极难正好重合,因此需要使用延拓的方法将其中一点归算到另一点。本文采用高精度的参考模型进行归算,如果归算到A点,则取A和B点处加速度模型值分别为aAm和aBm,假设
式中,aA0和aB0为t0时刻A和B点的加速度值;aA1和aB1为t1时刻A和B点的加速度值。则在A点处加速度的变化ΔaA可以由公式(2)表达 式中,ΔaA即为交叠点法中的观测量,为了计算低阶带谐系数的变化,还需要给出ΔaA和低阶带谐系数的微分关系式。

|
| 图 1 交叠点示意图 Fig. 1 The sketch map of crossover |
首先,直接给出地球重力场的引力位V的表达式[16]
式中,GM为地心引力常数;ae为地球赤道半径;r为计算点的地心距;λ和为地心经纬度;Cnm和Snm为Stokes系数;Pmn为缔合勒让德函数。 式中, 、
、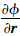 和
和 可由下式计算
另外,由公式(3)可推导
可由下式计算
另外,由公式(3)可推导 、
、 和
和 的表达式
进而可以得出低阶带谐项偏导数
的表达式
进而可以得出低阶带谐项偏导数 、
、 和
和 。在此仅给出2和3阶带谐项的偏导数表达式
。在此仅给出2和3阶带谐项的偏导数表达式将表达式(5)、式(7)和式(8)代入式(4)即得到加速度对2和3阶带谐系数的偏导数公式。实用上,可利用交叠点的加速度差计算观测时刻间低阶带谐系数的随时间变化。 3 交叠点覆盖以及轨道精度分析
交叠点的覆盖特性和LEO的径向轨道精度是交叠点法反演地球重力场时变信息的关键因素。以下将分别就LEO星群交叠点的覆盖特性和交叠点法对精密定轨精度的要求进行分析。 3.1 交叠点覆盖分析
由于地球重力场具有全球性的特点,因此数据的有效覆盖是利用卫星技术反演地球重力场的关键之一。为了评价LEO星群构成交叠点的覆盖特性,以COSMIC星座为例,选取前后相距30d的10对数据:2008.001-2008.010和2008.031-2008.040依次构成日对进行分析。以2008.001和2008.031日对为例,交叠点的配对规则如表 1所示。
| 2008.001
01星 |
2008.001
02星 |
2008.001
03星 |
2008.001
04星 |
2008.001
05星 |
2008.001
06星 |
| 2008.031
01星 |
|||||
| 2008.031
02星 |
2008.031
02星 |
||||
| 2008.031
03星 |
2008.031
03星 |
2008.031
03星 |
|||
| 2008.031
04星 |
2008.031
04星 |
2008.031
04星 |
2008.031
04星 |
||
| 2008.031
05星 |
2008.031
05星 |
2008.031
05星 |
2008.031
05星 |
2008.031
05星 |
|
| 2008.031
06星 |
2008.031
06星 |
2008.031
06星 |
2008.031
06星 |
2008.031
06星 |
2008.031
06星 |
通过配对后计算出1个日对和10个日对的COSMIC星座交叠点的覆盖情况如图 2所示。

|
| 图 2 交叠点地面覆盖 Fig. 2 The coverage of crossover points |
可以看出,1个日对的覆盖对于低阶位系数的计算已有足够的空间分辨率。而10个日对的覆盖可满足更高空间分辨率的要求。当然,由于COSMIC的主要任务是为气象服务的,并非为重力场探测专门设计,所以在一些区域交叠点的覆盖不够理想。这通过引入更多的LEO卫星和星座,形成真正的LEO星群来更好地满足覆盖的要求。 3.2 径向轨道精度分析
交叠点法的观测量是LEO的精密轨道,其轨道精度,特别是径向轨道精度对反演的影响最大,而非保守力模型化误差反而不是最主要的误差源。
表 2给出了800~500km,4种轨道高度,不同径向轨道误差(0.01~0.15m)对重力场观测精度的影响。其中,0.01m的精度在500km高度的配置情况与GRACE类似,而0.15m的精度在800km高度的配置与COSMIC类似。为了直观地分析时变重力场的量级,使用美国喷气动力实验室(Jet Propulsion Laboratory,JPL)公布的2008年1月—2008年2月GRACE Level2数据的单月重力场模型,分别计算了800km和500km轨道高度处,时变信号的大小如图 3所示。在800km轨道高度处,全球重力扰动变化量的绝对值之平均值为3.725×10-4mGal,最小值为-1.5×10-3mGal,最大值为3.5×10-3mGal。在500km轨道高度处,全球重力扰动变化量的绝对值之平均值为6.354×10-4mGal,最小值为-3.3×10-3mGal,最大值为5.7×10-3mGal。而由表 2可知在800km轨道高处,径向轨道误差依次为1cm、5cm、10cm和15cm将依次产生2.15×10-3mGal、10.8×10-3mGal、21.6×10-3mGal和32.3×10-3mGal的误差。
| 轨道高
度/km |
径向误差 | |||
| 0.01 m | 0.05 m | 0.10 m | 0.15 m | |
| 800.00 | 2.15×10 -3 | 10.8×10 -3 | 21.6×10 -3 | 32.3×10 -3 |
| 700.00 | 2.25×10 -3 | 11.2×10 -3 | 22.5×10 -3 | 33.7×10 -3 |
| 600.00 | 2.35×10 -3 | 11.7×10 -3 | 23.5×10 -3 | 35.2×10 -3 |
| 500.00 | 2.45×10 -3 | 12.2×10 -3 | 24.5×10 -3 | 36.7×10 -3 |

|
| 图 3 2008-01—2008-02全球重力扰动的变化 Fig. 3 The time-variable gravity disturbances of 2008-01 to 2008-02 |
综合表 2和图 2给出的信息可知,以目前COSMIC星座10~15 cm的轨道精度不能满足较高空间分辨率时变重力场反演的需要。如果能够将轨道高度降低或提高径向定轨精度将使COSMIC应用于较高分辨率的时变重力场研究。
4 模拟计算结果与分析
为了验证前述地球重力场低阶带谐系数交叠点法计算模型的正确性,进行了模拟计算。模拟方案如表 3所示。
| 项目 | 内容 | 说明 |
| 数值标准 | IERS 2003 | 包括坐标转换,时间系统转换等 |
| 数值
积分器 |
R-K 7(8)单步积分器Cowell 11阶多步积分器 | RK积分器作为起步积分器 |
| 参考重力
场模型 |
EGM 2008 | http://earth-info.nga.mil/ |
| TLE文件 | leoTLE_200 8.001.001 _txt
leoTLE_2008.001.002_txt leoTLE_2008.001.003_txt leoTLE_2008.001.004_txt leoTLE_2008.001.005_txt leoTLE_2008.001.006_txt |
http://www.cosmic.ucar.edu/ |
该方案以EGM2008[17, 18]为参考模型,轨道初始文件为2008.001的COSMIC第1-6号卫星TLE(two-line element)文件[19, 20]。轨道生成采用RK7(8)单步积分器起步,Cowell多步积分器进行精密轨道积分,积分间隔为1s,输出数据的步长为60s。依次生成6颗COSMIC卫星第2008.001和2008.031的模拟轨道。其中2008.001轨道的力模型采用EGM2008。2008.031轨道的力模型采用基于EGM2008的模拟时变模型,C02和C03的系数分别加上了1×10-12和1×10-15的模拟时变量。模拟中所使用的有关坐标变换及相关数值标准均遵循国际地球自转服务提供的IERS 2003标准[21]。
采用本文第2节的模型处理了由高精度数值积分器生成的1个日对(2008.001和2008.031)6颗COSMIC卫星的模拟轨道数据,得出的计算值与模拟时变量的比较如表 4所示。可以看出,本文所给出的计算模型本身的误差很小。
| 带谐系数 | 模拟时变量 | 计算值 |
| C20 | 1×10 -12 | 0.99897×10 -12 |
| C30 | 1×10 -15 | 1.10387×10 -15 |
利用LEO星群数据反演地球重力场低阶带谐项随时间变化的交叠点法需要数据的有效全球均匀覆盖。通过对COSMIC星座的分析,目前COSMIC星座在全球覆盖方面还存在空白区,而其定轨精度也不足以反应较高空间分辨率的地球重力场时变信号,若能在COSMIC Follow-on中进行改进,将定轨精度提高到与GRACE类似的厘米量级,将可以使用交叠点法恢复较高分辨率的地球时变重力场。进一步联合其他搭载了星载GPS接收机的LEO卫星或星座,且精密定轨精度在1cm量级,将可弥补COSMIC交叠点分布和轨道精度方面的不足。LEO星群获取的时变重力场信号将可作为GRACE时变观测资料的补充,甚至可作为可能出现的GRACE和GRACE Follow-on数据间断的替代,为地球科学领域提供连续的地球重力场时变信息。高精度数值积分模拟COSMIC卫星轨道的计算结果表明,本文给出的利用交叠点法反演重力场低阶带谐系数随时间变换的数学模型是正确的。
致谢:宁津生院士是我国著名大地测量学家,为国家测绘事业发展和人才培养作出了重要贡献。值此宁津生院士80华诞之际,特撰写此文以表达对他的崇高敬意,衷心感谢他对笔者10多年的培养。
| [1] | ADAM David. Gravity Measurement: Amazing Grace[J]. Nature, 2002, 416(6876):10-11. |
| [2] | NING Jinsheng. Following the Developments of the World, Devoting to the Study on the Earth Gravity Field[J]. Geomatics and Information Science of Wuhan University, 2001, 26(6):471-474. (宁津生. 跟踪世界发展动态 致力地球重力场研究[J]. 武汉大学学报:信息科学版, 2001, 26(6):471-474.) |
| [3] | CHEN Junyong, WEN Hanjiang, CHENG Pengfei. On the Development of Geodesy in China[J]. Geomatics and Information Science of Wuhan University, 2001, 26(6):475-428. (陈俊勇, 文汉江, 程鹏飞. 中国大地测量学发展的若干问题[J]. 武汉大学学报:信息科学版, 2001, 26(6):475-482.) |
| [4] | CHAO B F, PAVLIS E C, HWANG C H, et al. COSMIC: Geodetic Applications in Improving Earth’s Gravity Model[J]. Terrestrial, Atmospheric and Oceanic Sciences, 2000, 11(1):365-378. |
| [5] | XU Xiaohua, LUO Jia, SHI Chuang. Comparison of COSMIC Radio Occultation Refractivity Profiles with Radiosonde Measurements[J]. Advances in Atmospheric Sciences, 2009, 26(6): 1137-1145. |
| [6] | XU Xiaohua, LUO Jia, ZHANG Kefei. An Analysis of the Structure and Variation of the Tropopause over China with GPS Radio Occultation Data[J]. Journal of Navigation, 2011, 64:103-111. |
| [7] | HWANG C. Gravity Recovery Using COSMIC GPS Data: Application of Orbital Perturbation Theory[J]. Journal of Geodesy, 2001, 75:117-136. |
| [8] | HWANG C, HWANG L. Satellite Orbit Error due to Geopotential Model Error Using Perturbation Theory: Applications to ROCSAT-2 and COSMIC Missions[J]. Computers & Geosciences, 2002, 28: 357-367. |
| [9] | HWANG C, LIN T J, TSENG T P, et al. Modeling Orbit Dynamics of FORMOSAT-3/COSMIC Satellites for Recovery of Temporal Gravity Variations[J]. IEEE Transactions on Geosciences and Remote Sensing, 2008, 46(11):3412-3423. |
| [10] | LIN T J, HWANG C, TSENG T P, et al. Low-degree Gravity Change from GPS Data of COSMIC and GRACE Satellite Missions[J]. Journal of Geodynamics, 2012, 53:34-42. |
| [11] | JEKELI C H. The Determination of Gravitational Potential Differences from Satellite-to-satellite Tracking[J]. Celestial Mechanics and Dynamical Astronomy, 1999, 75:85-101. |
| [12] | HUANG Motao, GUAN Zheng, ZHAI Guojun, et al. The Self-calibrating Adjustment of Marine Gravity Survey Network[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(2):162-171. (黄谟涛, 管铮, 翟国君, 等. 海洋重力测量网自检校平差[J]. 测绘学报, 1999, 28(2):162-171.) |
| [13] | BAO Jingyang, CHAO Dingbo, LI Jiancheng. Tidal Harmonic Analysis near Crossovers of TOPEX/ POSEIDON Ground Track in South China Sea[J]. Acta Geodaetica et Cartographica Sinica, 2000, 29(1):17-23. (暴景阳, 晁定波, 李建成. 南中国海TOPEX/ POSEIDON 轨迹交叉点测高数据的潮汐调和分析[J]. 测绘学报, 2000, 29(1):17-23.) |
| [14] | LI Jiancheng, NING Jinsheng, CHEN Junyong, et al. Determination of Gravity Anomalies over the South China Sea by Combination of TOPEX/ Poseidon, ERS2 and Geosat Altimeter Data[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(3):197-202. (李建成, 宁津生, 陈俊勇, 等. 联合TOPEX/ Poseidon, ERS2 和Geosat卫星测高资料确定中国近海重力异常[J]. 测绘学报, 2001, 30(3):197-202.) |
| [15] | LUO Jia, NING Jinsheng. Analysis of Time-variable Gravity Field Exploring Performance with LEO Cluster[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6): 636-638. (罗佳, 宁津生. LEO星群探测地球重力场的性能分析[J]. 武汉大学学报:信息科学版, 2010, 35(6):636-638.) |
| [16] | HEISKANEN W A, MORITZ H. Physical Geodesy[M]. San Francisco: W H Freeman and Company, 1967. |
| [17] | NGA. Earth Gravity Model(EGM)2008[EB/OL].[2010-09-20]. |
| [18] | PAVLIS N K, HOLMES S A, KENYON S C, et al. An Earth Gravitational Model to Degree2160: EGM2008[R]. Vienna:EGU General Assembly, 2008. |
| [19] | NORAD. NORAD Two-line Element Set Format[EB/OL].[2004-08-30]. |
| [20] | UCAR. COSMIC Homepage[EB/OL]. [2010-09-26] |
| [21] | DENNIS D M, GERARD P. IERS Conventions (2003)[M]. Frankfurt am Main: Verlag des Bundesamts fur Kartographie und Geodasie, 2004. |