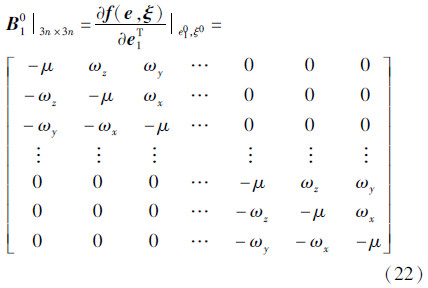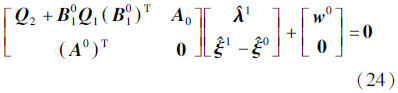2.同济大学现代工程测量国家测绘地理信息局重点实验室，上海200092
2.Key Laboratory of Advanced Surveying Engineering of National Administration of Surveying,Mapping and Geoinformation,Tongji University Shanghai 200092, China
1 引言
观测值中通常不可避免地会含有少量粗差。在平差过程中,若不消除粗差的影响,会使模型扭曲,结果错误,因此需要稳健的方法对粗差进行探测和定位。选权迭代是粗差探测的一种方法,其本质是将粗差归入随机模型中,选择稳健的权函数,通过迭代更新,使含粗差的观测值的权愈来愈小,从而达到粗差的自动定位和改正[1]。对于最小二乘(LS)中的粗差探测,国内外已经有了广泛和深入的研究。文献[2]总结了经典误差理论与抗差估计问题;文献[3]论述了大地测量相关观测抗差估计问题；文献[4]讨论了稳健估计等。
然而,以上这些方法都是在LS的计算过程中对粗差进行探测或剔除。在LS方法中,当有多余观测存在时,为了得到参数的最佳估值,通常采用经典的高斯-马尔科夫(G-M)模型对观测方程式Ax=b进行求解。G-M模型的前提是假设系数矩阵A没有误差,随机误差仅存在于观测向量b中。然而在很多实际情况中,该前提并不成立。总体最小二乘(TLS)方法同时考虑了观测向量和系数矩阵的误差。
TLS方法在求解观测方程时,除了要考虑观测向量b的误差外,还需考虑系数矩阵A的误差[5]。由于系数矩阵A中的变量通常也包含观测值,因此不可避免地存在误差。可见,TLS法相对于LS法而言,更加合理和完整。文献[6—8]对约束、加权的TLS方法进行了深入的研究；文献[9—10]推导了病态TLS的解法；文献[11]研究了附有相对权比的TLS方法。同时总体最小二乘方法也广泛应用于测量的各个方面[12, 13, 14, 15, 16]。
然而,以上对于TLS方法的研究仅限于观测向量和系数矩阵存在随机误差的情况,若观测向量b和系数矩阵A中含有个别粗差,直接采用TLS方法则会使模型歪曲造成参数估计严重失实。鉴于此,针对EIV模型中观测向量b和系数矩阵A中含有个别粗差的情况,本文提出基于选权迭代的稳健TLS方法。文献[17—18]均利用IGG(周江文法)权函数,在基于奇异值分解方法的基础上对混合最小二乘和总体最小二乘(LS-TLS)进行演算。然而此时,观测向量b和系数矩阵A的权必须是相等的。本文提出利用基于非线性高斯-赫尔墨特(G-H)LS平差的TLS解来解算选权迭代的TLS方法,此时观测向量b和系数矩阵A可不等权,并且该计算过程可同时针对TLS或LS-TLS。
本文以三维相似坐标变换为例,针对观测向量和系数矩阵同时存在随机误差和粗差的情况,推导了基于选权迭代的稳健TLS方法。通过模拟数据的计算,证明利用本文提出的基于选权迭代的稳健TLS法能够准确地进行粗差定位,并且较快地收敛于准确的参数解。 2 稳健总体最小二乘估计模型 2.1 基于非线性G-H LS平差的总体最小二乘解
TLS求解主要有奇异值分解法[5]和经典的拉格朗日方法[7, 19],也可以作为非线性G-H模型处理[20, 21],即在非线性观测方程中对未知参数和随机误差进行线性化,应用LS,通过交替迭代,得到非线性G-H模型下由LS平差获得的TLS解,它的计算模型为
设由随机误差向量e和未知参数ξ组成的观测方程为
令随机误差向量和未知参数的近似值分别为e0和ξ0,则式(1)线性化为[20]
式中,
;方程的常数项为
这里,系数矩阵B0既包含了对观测向量误差的导数,也包含了对系数矩阵误差的导数,随机误差e既包含了观测向量的误差eb,也包含了系数矩阵的误差eA,eb和eA满足
eb和eA均服从正态分布,在经典的LS中,EA≡0。vec 是指将矩阵按列拉直所得到的列向量,排列的顺序为从左至右。σ02为方差,Qb和QA为协因数阵。则观测方程[20]为
式中,常数向量w0∈Rn×1；系数矩阵A0∈Rn×m；系数矩阵B0∈Rn×n(m+1)；参数向量ξ∈Rm×1；误差向量e∈Rn(m+1)×1。 TLS的目标函数为
利用拉格朗日乘数λ,构成新的目标函数
要使φ′最小,则φ′关于e和ξ的偏导数应等于零,即
经过整理,可得如下方程[20]
求解式(9),可得未知参数1和拉格朗日乘数1,相应的误差向量为[20]
将1和1作为新的初值,代入式(10)重新计算,直到满足收敛条件。 2.2 基于选权迭代的总体最小二乘方法
以上的解算是在观测向量b和系数矩阵A仅存在随机误差的前提下进行的,若b和A不仅存在随机误差,且存在粗差,则模型会歪曲,造成参数估计严重失实。稳健LS方法,仅可对b中的粗差进行探测和定位；而稳健TLS方法,可同时处理A和b中的粗差。
权函数有各种不同的形式。经试验证明,无论采用何种常用的权函数,如Huber权函数、周江文(IGG)权函数、Hample权函数等,在参数选取合理且粗差大于最小可探测偏差(MDB)时,利用本文的稳健TLS方法均能准确定位粗差。这里以Huber权函数为例[4]
式中,v为迭代次数；c为单位权方差0的函数,c=δ·0,δ为一常数,一般取δ=2。
将Huber法用于TLS方法中,需要对系数矩阵A和观测向量b的权阵分别进行计算。因此,设系数矩阵A和观测向量b的权阵为P1和P2,可表示为
选权迭代的稳健TLS方法的平差过程从加权TLS法开始,在每次平差后,按所选择的权函数计算每个观测值在下次迭代平差中的权。如果权函数选择得当,且粗差大于最小可探测偏差,则无论是存在于系数矩阵A,还是存在于观测向量b中的粗差均可准确定位,且含粗差的观测值的权将愈来愈小。 2.3 三维相似坐标变换的稳健总体最小二乘解
若(x2,y2,z2)和(x1,y1,z1)分别为控制点在目标坐标系和原坐标系下的坐标,(X0,Y0,Z0)为平移量；μ为尺度参数；(ωx,ωy,ωz)分别代表了绕3个轴的旋转角,则三维相似坐标变换的Bursa模型可表示为
假定目标坐标系和原坐标系下,第i点的坐标为(x2i,y2i,z2i)和(x1i,y1i,z1i),相应的随机误差分别为(ex1,i,ey1,i,ez1,i)和(ex2,i,ey2,i,ez2,i),则坐标变化关系式可表示为
因此误差向量e为
若目标坐标系和原坐标系下观测值的协因数阵分别为Q2和Q1,权阵分别为P2和P1,则式(15)所表达的TLS目标函数可表示为
将坐标转换关系式(14)表示为方程
若误差向量和未知参数的初值分别为e0和ξ0,则对式(17)线性化后可得
式中,
常数向量为[20]
由此可组成方程组如下
通过解算,获得未知参数和拉格朗日乘数,相应的改正数为
通过迭代,直到参数向量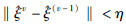
,通常取η=10－10。
加权单位权方差及参数精度为
式(26)计算的单位权方差是有偏的,偏差可以通过数值计算的方法得到[19]。由于偏差较小,对本文的结果没有影响,这里不进行计算。 3 模拟计算分析
本例采用模拟计算的方法,对三维相似坐标变换采用稳健TLS方法予以实现。模拟的数据为：中心处于原坐标系原点,各边与坐标轴平行,边长为2000 m的正立方体, 因此是在原坐标系中均匀分布的27个等精度观测的标准点(如图 1),模拟的坐标转换参数为：(X0,Y0,Z0)=(100.000 0,100.000 0,100.000 0)；μ=1.001；(ωx,ωy,ωz)=(0.002,0.005,0.008)单位为(°)。
|
| 图 1 控制点在原坐标系和目标坐标系下的分布情况 Fig. 1 The distribution of control points in the source and target coordinate system |
(1) 以第4点存在粗差为例。给4号点在目标坐标系和原坐标系下的坐标值加入粗差(0.300 0,0.400 0,0.500 0)和(-0.300 0,-0.400 0,-0.500 0)粗差单位m,其余点坐标仅含σ0=0.01 m,且P1=I81,P2=1∕4P1的服从正态分布的随机误差。分别利用LS、稳健LS、TLS、稳健TLS得到的坐标转换参数与真值的差值及结果的精度如表 1、表 2所示。
| 参数 | LS | 稳健LS | TLS | 稳健TLS |
| dX 0/mm | -26.034 8 | -8.224 5 | -26.034 8 | -5.943 8 |
| dY 0/mm | -20.124 7 | 4.257 4 | -20.124 7 | 6.515 1 |
| dZ 0/mm | -43.099 3 | -13.152 4 | -43.099 3 | 10.872 2 |
| dμ/(×10 -6) | -0.000 015 | -0.000 003 | -0.000 015 | 0.000 002 |
| dω x/(″) | -5.549 612 34 | -0.917 455 39 | -5.549 612 24 | -0.564 770 50 |
| dω y/(″) | -0.226 129 68 | -0.226 649 45 | -0.226 129 90 | -0.226 673 74 |
| dω z/(″) | 4.089 906 89 | 1.334 369 35 | 4.089 906 83 | 0.981 533 73 |
从表 1的结果可知,利用选权迭代的方法计算得到的坐标转换参数与真值的差值比无选权迭代的方法计算的差值小,即通过选权迭代,粗差的影响减小,使得计算结果更接近于真值。而相比于稳健LS,稳健TLS方法计算的参数值与真值最为接近。
表 2的精度结果进一步展示了稳健TLS方法计算结果最为可靠。LS和TLS方法计算的参数结果一致,因此参数精度也相同；相比于经典的方法,稳健LS和稳健TLS精度均更高。
| 参数 | LS | 稳健LS | TLS | 稳健TLS |
| X 0/m | 0.030 729 65 | 0.013 866 14 | 0.030 729 65 | 0.011 018 76 |
| Y 0/m | 0.030 729 65 | 0.013 878 42 | 0.030 729 65 | 0.011 023 70 |
| Z0/m | 0.030 729 65 | 0.013 887 96 | 0.030 729 65 | 0.011 029 03 |
| μ | 0.000 021 73 | 0.000 009 74 | 0.000 021 73 | 0.000 007 73 |
| ωx/(°) | 0.000 026 61 | 0.000 011 98 | 0.000 026 61 | 0.000 009 51 |
| ωy/(°) | 0.000 026 61 | 0.000 011 83 | 0.000 026 61 | 0.000 009 38 |
| ωz/(°) | 0.000 026 61 | 0.000 011 96 | 0.000 026 61 | 0.000 009 50 |
| 0 | 0.159 676 | 0.070 990 | 0.130 371 | 0.039 813 |
而在收敛性方面,稳健LS、稳健TLS的在迭代5次后‖ξ5-ξ4‖ < 10－10,因此,利用稳健TLS方法能够较快地收敛于正确的参数解。
(2) 对一组模拟数据进行分析。此时,4号点在目标坐标系和原坐标系下的粗差值为(0.300 0,0.400 0,0.500 0)和(-0.300 0,-0.400 0,-0.500 0)粗差单位m。对该情况模拟出1000组数据,采用选权迭代的稳健TLS予以计算,得到的4号点在两个坐标系下的残差值如图 2所示。
|
| 图 2 4号点在目标坐标系和原坐标系下的坐标残差图 Fig. 2 Residuals of the 4th point in target and source coordinate system |
由图 2结果可见,4号点的残差值与加入的粗差值相符,即残差分别在(0.300 0,0.400 0,0.500 0)和(-0.300 0,-0.400 0,-0.500 0)附近波动。坐标转换参数与真值的差值如图 3。
|
| 图 3 计算得到的坐标转换参数与真值的差值 Fig. 3 Difference of computed transformation parameters using the robust TLS solution from their true values |
由图 3可知,这1000组数据计算出的坐标转换参数稳定,与真值较为接近。
(3) 当两个坐标系下有一个对应点存在粗差时,共有27种情况。最后对这27种情况进行计算,研究粗差点在不同位置时,利用稳健TLS方法能否计算出准确的残差值。
在第i种情况下,给第i个点在目标和原坐标系下的坐标分别加入(0.300 0,0.400 0,0.500 0),和(-0.300 0,-0.400 0,-0.500 0)粗差,单位m。利用稳健TLS方法计算得到坐标残差值如图 4。
|
| 图 4 两坐标系下有一个对应点坐标值含有粗差的残差图 Fig. 4 Residuals of points in two coordinate systems when there is one point containing gross error |
从图 4的结果可以看到,无论粗差点位于坐标系哪个位置,利用本文的稳健TLS均能准确探测出该粗差点,并且计算的残差值与加入的粗差相符。而不含粗差点的残差值在零附近波动。最后计算出的坐标转换参数与真值相近。 3.2 原坐标系和目标坐标系下有两个对应点坐标值含有粗差
以第4号点和第5号点存在粗差为例。给4号点和5号点在目标坐标系和原坐标系下的坐标值均加入粗差(0.300 0,0.400 0,0.500 0)和(-0.300 0,-0.400 0,-0.500 0)粗差单位m,其余点含随机误差。分别利用LS、稳健LS、TLS、稳健TLS计算的坐标转换参数与真值的差值如表 3。
| 参数 | LS | 稳健LS | TLS | 稳健TLS |
| dX 0/mm | -42.467 6 | -19.236 2 | -42.467 6 | -10.044 4 |
| dY 0/mm | -63.350 4 | -24.294 9 | -63.350 4 | -15.105 3 |
| dZ 0 /mm | -72.644 9 | -20.366 9 | -72.644 9 | -11.177 5 |
| dμ/(×10 -6) | 0.000 000 | 0.000 000 | 0.000 000 | 0.000 000 |
| dω x/(″) | -0.347 093 85 | -0.654 934 02 | -0.347 093 73 | -0.654 902 96 |
| dω y/(″) | -1.841 271 36 | -1.840 675 99 | -1.841 271 81 | -1.840 592 02 |
| dω z/(″) | -0.776 575 68 | -0.782 236 40 | -0.776 575 69 | -0.782 176 07 |
同样的,从表 3和表 4的结果可见,相比于其他3种方法,利用稳健TLS计算结果更接近于真值。而因为粗差点的增加,存在两个粗差点的结果要差于仅存在一个粗差点的结果。
| 参数 | LS | 稳健LS | TLS | 稳健TLS |
| dX 0/mm | -62.146 4 | -44.650 4 | -62.146 4 | -22.989 6 |
| dY 0/mm | -91.587 5 | -53.810 5 | -91.587 5 | -31.976 2 |
| dZ 0/mm | -109.870 1 | -49.056 2 | -109.870 1 | -27.403 5 |
| dμ /(×10 -6) | 0.000 028 | 0.000 015 | 0.000 028 | 0.000 007 |
| dω x/(″) | -3.871 372 77 | -2.158 589 29 | -3.871 372 46 | -0.917 701 06 |
| dω y/(″) | 2.270 319 31 | -0.024 433 42 | 2.270 318 66 | -0.023 819 33 |
| dω z/(″) | 6.071 869 42 | 4.035 900 36 | 6.071 869 33 | 2.795 273 36 |
通过1000组模拟数据,利用基于选权迭代的稳健TLS计算出的4号点和5号点的坐标残差值与加入的粗差值相符,且计算得到的坐标转换参数稳定,与真值较为接近。
27个点中任意两点在两个坐标系下存在粗差共有351种情况。由于数据量较大,这里不对结果进行展示。经过计算证明,无论是哪两点存在粗差,即无论两个粗差点的分布如何,利用本文的基于选权迭代的稳健总体最小二乘方法均能准确探测出该粗差点,并且计算的残差值与加入的粗差相符。两个粗差点的位置及分布对最后计算出的坐标转换参数没有影响。 3.3 原坐标系和目标坐标系下有更多对应点坐标值含有粗差
随着粗差个数的增加,无论利用何种方法计算的坐标转换参数必然与真值相差越来越大。例如,当有3个点(第4、第5和第14号点)和4个点(第4、第5、第14和第15号点)存在与上文相同的粗差时,计算得到的坐标转换参数与真值的差值分别如表 3和表 4。
从表 4和表 5的结果可以看到,虽然相比其他3种方法,本文的稳健TLS方法的计算结果与真值最为接近,且精度较高,但随着粗差点个数的增加,计算结果与真值的差距受到粗差的影响而越来越大。例如当有4个点存在粗差时,利用稳健TLS计算出的坐标转换参数平移量均接近或超过0.5 m。然而从计算结束时的权函数中仍可探测出粗差的位置,因此,当且仅当控制点数量足够多的情况下,若要准确计算出坐标转换参数,可将探测出的粗差点剔除后,再利用余下的点进行计算。
| 参数 | LS | 稳健LS | TLS | 稳健TLS |
| dX 0/mm | -91.418 5 | -90.329 3 | -91.418 5 | -58.566 9 |
| dY 0/mm | -124.563 9 | -96.727 0 | -124.563 9 | -57.594 5 |
| dZ 0/mm | -148.266 0 | -89.742 8 | -148.266 0 | -50.443 6 |
| dμ/(×10 -6) | 0.000 024 | 0.000 028 | 0.000 024 | 0.000 019 |
| dω x/(″) | -1.406 287 54 | -0.827 582 56 | -1.406 287 33 | -0.827 679 85 |
| dω y /(″) | 12.156 897 98 | 7.862 655 71 | 12.156 896 97 | 4.746 913 90 |
| dω z /(″) | 8.887 878 88 | 6.903 567 21 | 8.887 878 63 | 4.178282 30 |
(1) 将稳健估计的原理加入TLS方法中,可以准确地对观测向量和系数矩阵中的粗差进行探测和定位。
(2) 由于TLS方法建立的EIV模型对所有变量中的误差都进行了最小化的约束,因此,将该方法应用于坐标转换中更加符合实际情况,计算的结果也更加合理。
(3) 从结果看,利用稳健TLS方法计算的结果准确度最高；而从迭代中止时点坐标的残差值看,当存在一定量的粗差时,利用稳健TLS方法可以准确地定位粗差的位置,且计算出的坐标残差值与加入的值相符。
(4) 随着粗差点个数的不断增加,计算出的坐标转换参数与真值差距逐步增大。但在一定范围内,利用稳健TLS方法仍可定位粗差的位置。若要准确计算出坐标转换参数,则应将探测出的粗差点剔除后,再利用余下的点进行计算。
(5) 通过对1~4个粗差点在坐标系不同位置的情况进行计算和分析,证明了利用稳健TLS方法计算坐标转换参数的结果与粗差点位分布无关。
| [1] | LI Deren, YUAN Xiuxiao. Error Processing and Reliability Theory[M]. Wuhan, Wuhan University Press, 2002, 240-255. (李德仁, 袁修孝. 误差处理与可靠性理论[M]. 武汉:武汉大学出版社, 2002, 240-255.) |
| [2] | ZHOU Jiangwen. Classical Theory of Errors and Robust Estimation[J]. Acta Geodaetica et Cartographica Sinica, 1989, 18 (2): 116-120. (周江文.经典误差理论与抗差估计[J]. 测绘学报, 1989, 18(2): 116-120.) |
| [3] | YANG Yuanxi. Robust Parameter Estimation for Geodetic Correlated Observations[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31 (2): 95-99. (杨元喜.大地测量相关观测抗差估计理论[J]. 测绘学报, 2002, 31(2): 95-99.) |
| [4] | PETER J H.Robust Statistics[M].Hoboken:John Wiley &Sons, 1981. |
| [5] | GOLUB H G, VAN LOAN F C. An Analysis of the Total Least Squares Problem[J]. SIAM Journal on Numerical Analysis, 1980, 17(6): 883-893. |
| [6] | SCHAFFRIN B. A Note on Constrained Total Least-Squares Estimation[J]. Linear Algebra and Its Applications, 2006(417): 245-258. |
| [7] | SCHAFFRIN B, FELUS Y A. An Algorithmic Approach to the Total Least-Squares Problem with Linear and Quadratic Constraints[J]. Studia Geophysica et Geodaetica, 2009, 53(1):1-16. |
| [8] | SCHAFFRIN B, WIESER A. On Weighted Total Least-Squares Adjustment for Linear Regression[J]. Journal of Geodesy, 2008, 82(7):415-421. |
| [9] | WANG Leyang, XU Caijun, LU Tieding. Ridge Estimation Method in Ill-posed Weighted Total Least Squares Adjustment[J]. Geomatics and Information Science of Wuhan University, 2010, 35 (11): 1346-1350. (王乐洋, 许才军, 鲁铁定. 病态加权总体最小二乘平差的岭估计解法[J]. 武汉大学学报:信息科学版, 2010, 35 (11): 1346-1350.) |
| [10] | GE Xuming, WU Jicang. Generalized Regularization to Ill-posed Total Least Squares Problem[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41 (3): 372-377. (葛旭明, 伍吉仓. 病态总体最小二乘问题的广义正则化[J]. 测绘学报, 2012, 41(3): 372-377.) |
| [11] | WANG Leyang, XU Caijun. Total Least Squares Adjustment with Weight Scaling Factor[J]. Geomatics and Information Science of Wuhan University, 2011, 36 (8), 887-890. (王乐洋, 许才军. 附有相对权比的总体最小二乘平差方法[J]. 武汉大学学报:信息科学版, 2011, 36 (8): 887-890.) |
| [12] | FELUS Y A, SCHAFFRIN B. Performing Similarity Transformations Using the Error-in-Variables Model[C]//Proceedings of ASPRS 2005 Annual Conference. Baltimore:[s.n.], 2005:7-11. |
| [13] | LU Jue, CHEN Yi, ZHENG Bo. Research Study on Three-dimensional Datum Transformation Using Total Least Squares[J]. Journal of Geodesy and Geodynamics, 2008, 28(5), 77-81. (陆珏, 陈义, 郑波. 总体最小二乘方法在三维坐标转换中的应用[J]. 大地测量与地球动力学, 2008, 28(5): 77-81.) |
| [14] | CHEN Yi, LU Jue, ZHENG Bo. Application of Total Least Squares to Space Resection[J]. Geomatics and Information Science of Wuhan University, 2008, 33 (12):1271-1274. (陈义, 陆珏, 郑波. 总体最小二乘方法在空间后方交会中的应用[J]. 武汉大学学报:信息科学版, 2008, 33 (12): 1271-1274.) |
| [15] | YANG Hongsen. Infrared Image Denoise Based on Total Least Squares[J]. Laser and Infrared, 2008, 38 (9): 961-964. (杨鸿森. 基于总体最小二乘的红外图像去噪方法[J]. 激光与红外, 2008, 38 (9): 961-964.) |
| [16] | YUAN Qing, LOU Lizhi, CHEN Weixian. The Application of the Weighted Total Least-squares to Three Dimensional-Datum Transformation[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S1): 115-119. (袁庆, 楼立志, 陈玮娴. 加权总体最小二乘在三维基准转换中的应用[J]. 测绘学报, 2011, 40(S1): 115-119.) |
| [17] | KANG Xiaofeng, ZHANG Huaping A Method of Selecting Weight Iteration Based on LS-TLS[J]. Applied Mechanics and Materials, 2011, 90-93: 2832-2835. |
| [18] | WU W Y, KANG C L. The Theory of Selecting Weight Iteration Based on LS-TLS Applied in Road Line Type Identification[C]//Proceedings of 2011 IEEE International Conference on Computer Science and Automation Engineering.Shanghai: IEEE, 2011:353-356. |
| [19] | SHEN Yunzhong, LI Bofeng, CHEN Yi. An Iterative Solution of Weighted Total Least-Squares Adjustment[J]. Journal of Geodesy, 2011, 85(4):229-238. |
| [20] | NEITZEL F. Generalization of Total Least-Squares on Example of Unweighted and Weighted 2D Similarity Transformation[J]. Journal of Geodesy, 2010, 84(12): 751-762. |
| [21] | WOLF P R, GHILANI C D. Adjustment Computations: Statistics and Least Squares in Surveying and GIS[M]. New York:Wiley-interscience Publication, 1997: 423-440. |