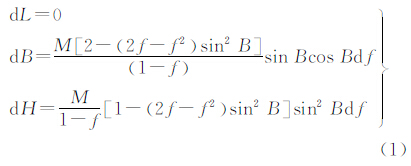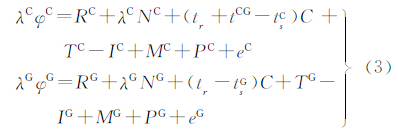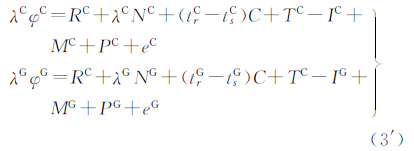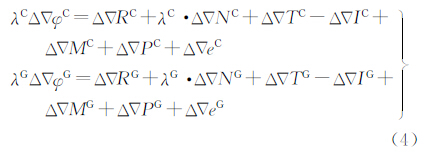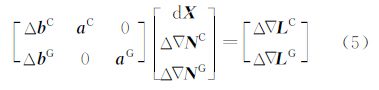2. 清华大学，北京 100084；
3.山东北斗华宸导航技术有限公司，山东 淄博 255088
2. Tsinghua University, Beijing 100084, China;
3. Shandong Compstar Navi-technology Limited Company, Shandong 255088, China
1 引 言
北斗卫星导航系统是中国自主研制开发的、具有自主知识产权的卫星导航定位系统，是继美国的GPS全球定位系统、俄罗斯的GLONASS之后，国际上可定位的第3个卫星导航系统。 北斗卫星导航试验系统(北斗一号)已于2005年建成，正在建设的北斗卫星导航定位系统(北斗二号一期)是由5颗GEO卫星、3颗IGSO卫星和4颗MEO卫星组成，覆盖中国境内及周边地区。其建设与发展将遵循开放性、自主性、兼容性、渐进性原则。为用户提供高质量的定位、导航和授时服务，并具有短报文通信功能[1]。目前已经发射9颗北斗卫星，在轨可工作卫星己有7颗，其中4颗GEO卫星、3颗IGSO卫星。因此，北斗区域卫星导航系统的基本系统已经建立，已经具备我国范围内初步三维定位导航能力。为了测试和验证目前北斗II系统在高精度相对定位方面的定位精度，本文首先对北斗和GPS联合高精度定位的相关问题进行了阐述，然后用清华大学和山东北斗华宸导航技术有限公司联合开发的BeiDou/GPS/GLONASS三系统双频高精度接收机，进行了BeiDou/GPS实测数据的采集与高精度处理，最后对测试结果进行了分析总结。试验结果不但验证了本文方法的正确性，也说明目前的北斗二号一期系统已经基本具备高精度的区域定位导航能力。但由于卫星数量和分布的不均匀，整体能力仍稍逊于GPS系统，随着后期的北斗卫星的不断发射与系统的完善，这些问题将迎刃而解。
2 定位采用的基准不同的卫星定位系统有特定的坐标基准和时间基准。北斗采用的是CSCS2000国家大地坐标系统和北斗时间系统(BeiDouT)；GPS采用的是WGS-84坐标系统和GPS时间系统(GPST)[2,3]。在北斗和GPS联合解算时，应将二者的坐标基准和时间基准进行转换和统一。
(1) CGCS2000与WGS-84坐标系在原点、尺度、定向及定向的定义都是相同的。参考椭球非常相近，在4个椭球常数a、f、GM、ω中，唯有扁率 f 有微小差异(df)
扁率变化对大地经度L、大地纬度B和大地高H的影响为
通过上面的公式，可得出：① df不引起大地经度变化；② df引起大地纬度的变化范围为0～0.105 mm；③ df引起大地高的变化范围为0～0.105 mm。因此，在当前的坐标测量精度(±1 mm)条件下，从理论上来说，由两个坐标系的参考椭球的扁率差异引起同一点在WGS-84和CGCS2000坐标系内的坐标变化，对于短距离的相对定位可以忽略。
(2) BeiDouT和GPST都采用原子时，秒长定义一样，没有闰秒问题。不同的是二者时间系统的起算点不同。GPST是从1980-01-06T00：00开始起算，并且无闰秒。而世界协调时有闰秒问题，到2006年GPST与世界协调时之间的闰秒差异已达到14 s。BeiDouT是从2006-01-01T00：00开始起算，没有闰秒问题[1]。因此，BeiDouT与GPST除了相差1356周外，还始终保持一个14 s的系统差，二者之间的转换关系为
3 定位算法 3.1 广播星历与卫星位置计算
GPS广播星历数据格式采用标准的RINEX格式，目前常用版本有RINEX 2.x和RINEX 3.x。由于北斗系统正在建设中，所以既便是最新的RINEX 3.1中也没有对北斗数据格式明确的规定。但由于北斗二代系统采用与GPS相类似的定位原理和卫星轨道参数，因此通常是参照GPS的相关说明，按RINEX 3.1中GPS的形式，编写北斗广播星历文件，只是在卫星号前分别用字母“G”和“C”区分GPS卫星和北斗卫星。同时，采用BeiDouT表示北斗卫星的参考时刻，采用CGCS 2000坐标基准表示北斗卫星的轨道信息。
北斗卫星星座共包括3类卫星：地球静止轨道(GEO)卫星、倾斜地球同步轨道(IGSO)卫星和中等高度地球轨道(MEO)卫星。其中IGSO和MEO卫星的瞬时位置计算与GPS的类似，GEO卫星稍有不同，主要是轨道倾角对同步轨道带来的影响。
3.2 定位解算模型 3.2.1 北斗和GPS单独定位高精度的卫星定位都是基于载波相位观测值的，北斗和GPS的载波相位观测方程为
式中，λ为载波波长；φ为载波相位观测值；R为卫星到接收机相位中心的几何距离；N为载波模糊度；tr为接收机的钟差；tCG为BeiDouT与GPST之间的同步误差；ts为卫星的钟差；C为光速；T为对流层延迟误差；I为电离层延迟误差；M为多路径误差；P为天线相位中心偏差；e为其他非模型化误差和载波相位观测噪声;上标C和G分别用于区分BeiDou和GPS。不同的载波频率对应不同的载波波长：BeiDou的双频频率分别为B1:1561.098 MHz，B2:1207.140 MHz；GPS的双频频率分别为L1:1575.42 MHz，L2:1227.60 MHz。在实际定位中，公式(3)中的时间系统同步误差项会被接收机钟差项吸收，相当于下面的式子 即含有不同的接收机钟差项trC和trG。
一般情况下，由于式(3)中含有过多的未知数和误差信息，所以造成定位解算的效率和精度并不是很好。为了提高定位精度，实际使用中最常采用的方法是分别用式(3)在2颗卫星和2台接收机间求二次差，得到如下的双差观测方程
式中，各符号含义与式(3)相同，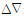
表示双差算子。双差观测方程的优点是消除了接收机钟差和卫星钟差的影响，消除了大部分电离层延迟和对流层延迟误差等系统误差，并且保持了载波模糊度的严格整周特性。
3.2.2 北斗和GPS联合定位
北斗和GPS联合定位时，首先要解决2个系统的基准问题，必须采用统一的时间基准和坐标基准，即可统一采用WGS-84坐标系和GPST基准，也可以采用CGCS2000坐标系和BeiDouT基准。由第2节的说明和分析可知，最新的WGS-84与CGCS2000的系统差异理论上在0～0.105 mm范围内，对于短距离的相对定位来说，完全可以忽略。其次在时间基准同步时，由于BeiDouT与GPST之间还存在微小的同步误差。为了消除不同卫星系统对定位的影响，这里双差组合仅限定在同一系统内部，即对于BeiDou系统可以得到类似式(4)的方程组，对于GPS系统，也可得方程(4)的方程组，然后进行联立可得BeiDou/GPS双差载波相位观测方程。对于相对定位中的双差观测方程，由于彻底消除了卫星钟差和接收机钟差影响，并且在站间距离较近，多路径误差有效抑制或可以忽略的情况下，双差观测方程中只剩下三维相对位置、整周模糊度未知数。另外，需要说明的是天线相位中心偏差，其值由天线厂商提供或者事先精确标定，结合天线定向安置进行影响修正与消除。因此，简化后的BeiDou/GPS双差载波相位观测方程为
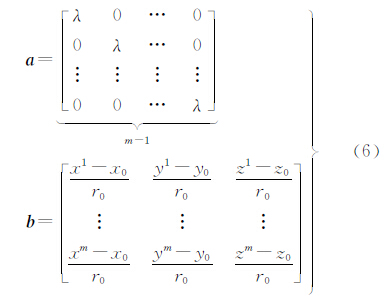
式中 式(5)中，dX表示相对坐标改正向量；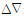
N为双差整周模糊度向量；b为与dX相对应的系数矩阵；a为与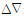N相对应的系数矩阵；L为常数项向量，其中Δ为单差算子。式(6)中，(x0,y0,z0)为用户位置初值；xm,ym,zm为卫星坐标；r0为用户位置初值与卫星之间的几何距离；m为观测到的同一系统卫星数。由于限定于同一系统内部求差，所以m颗GPS卫星可得到m－1个GPS双差观测方程，n颗北斗卫星可得到n－1个北斗双差观测方程，共m+n－2个观测方程。对于式(5)的求解可以采用最小二乘法或卡尔曼滤波的形式，可参考相关文献[4, 5]，这里不再赘述。一般是先求出双差整周模糊度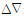N[6, 7, 8, 9]，然后再求出相对坐标改正值，进而得到精确的相对位置信息。
4 实测结果与分析
4.1 数据采集2011-09-29，采用清华大学和山东北斗华宸导航技术有限公司联合开发的BeiDou/GPS/GLONASS三系统双频高精度接收机，在山东潍坊进行了A、B 2点的短基线相对定位试验。基线长度为1031 m，数据采样率为1 Hz，卫星高度截止角为15°。为了将北斗定位结果与GPS进行比较，选择了GPS比较具有代表性的一段观测数据，数据观测时间将近2 h，接收和使用的卫星为：北斗卫星，1、3、4、7、8；GPS卫星，3、6、7、8、11、13、16、19、23、24。
与GPS系统不同的是，北斗系统的卫星由不同类型的卫星组成，其中的1、3、4号卫星属于GEO卫星，7和8号卫星属于IGSO卫星。因本次试验重点分析北斗和GPS卫星的定位情况，故没有对GLONASS数据进行处理。
4.2 数据处理(1) 坐标参考值：为了对目前的北斗系统高精度定位情况进行精确比较，首先对其中的GPS数据及周边国际IGS站数据，采用精密星历和GAMIT软件进行静态基线处理，得到A点和B点的准确的坐标及其基线分量值，作为真值，以便后面的定位结果与此进行比较；
(2) 坐标初值：GPS的坐标初值可以采用单点定位的方式确定，而关于北斗的坐标初值确定有两种方法，一种方法是由GPS提供，另外一种方法是北斗单独进行单点定位提供。需要说明的是北斗的单点定位精度。笔者在2011年5月份进行了的实测数据处理与比较，当时卫星情况与本文的实验情况类似，可以接收到4、5颗有效北斗卫星。由于篇幅所限，这里只给出最终的BeiDou/GPS单点定位结果(如表 1)，此结果采用北斗和GPS等权处理。从表 1可以看出，单独利用北斗进行初值确定也是完全可以的，另外还可以通过伪距差分方式进一步提高初值精度。
| m | |||
| N分量误差 | E分量误差 | U分量误差 | |
| GPS | 1.846 8 | 1.610 1 | 3.927 7 |
| BeiDou | 12.737 8 | 2.429 4 | 20.562 7 |
| BeiDou/GPS | 2.512 7 | 1.403 6 | 8.626 7 |
(3) 整周模糊度：如3.2节所述，整周模糊度的快速准确确定是高精度载波相位定位的首要前提条件，由于北斗系统与GPS系统类似，所以GPS的模糊度搜索方法同样适用于北斗模糊度搜索，如LAMBDA方法、单历元整周模糊度搜索方法等[6, 7, 8]。
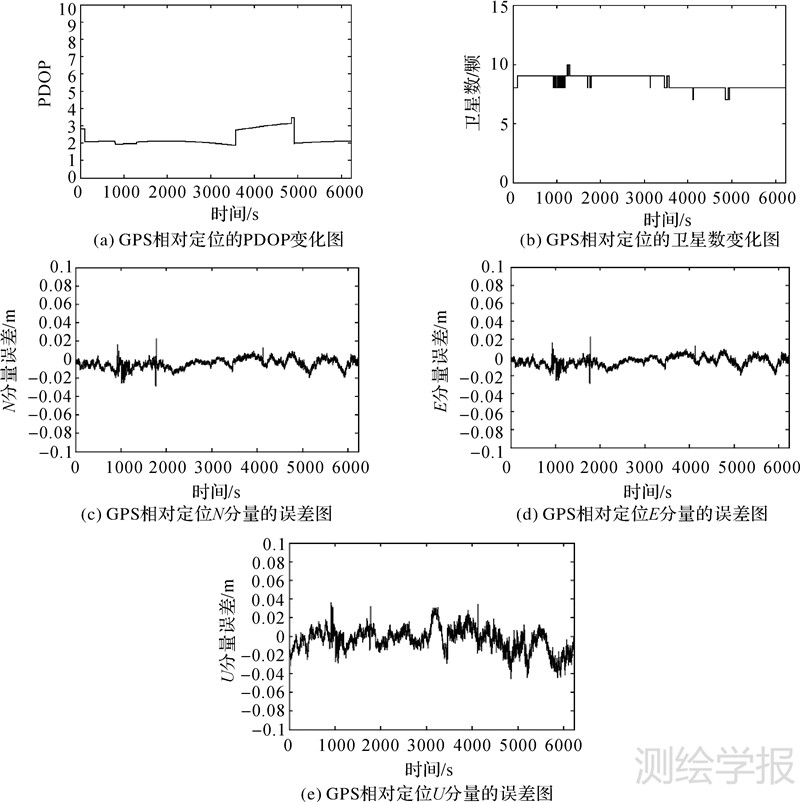
(4) 定位结果：准确固定整周模糊度后，首先对GPS数据进行最小二乘解算，可以得到每历元GPS高精度相对定位结果，与GAMIT定位结果进行比较，可得到AB基线在北(N)、东(E)、天顶(U)3个方向上的误差值，如图 1～图 3。
|
| 图 1 Fig. 1 |
|
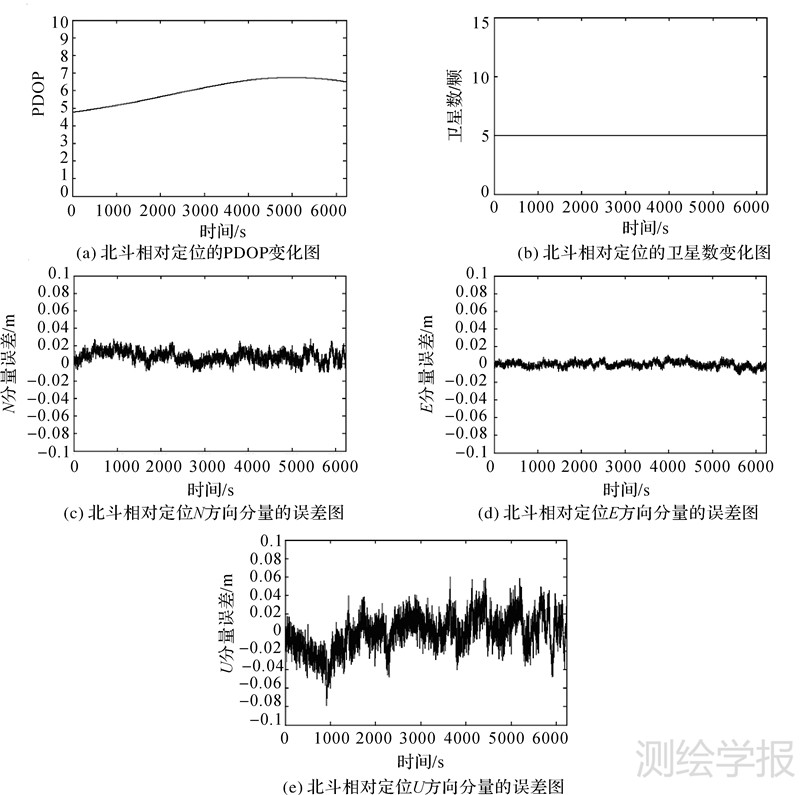
| 图 2 Fig. 2 |
|
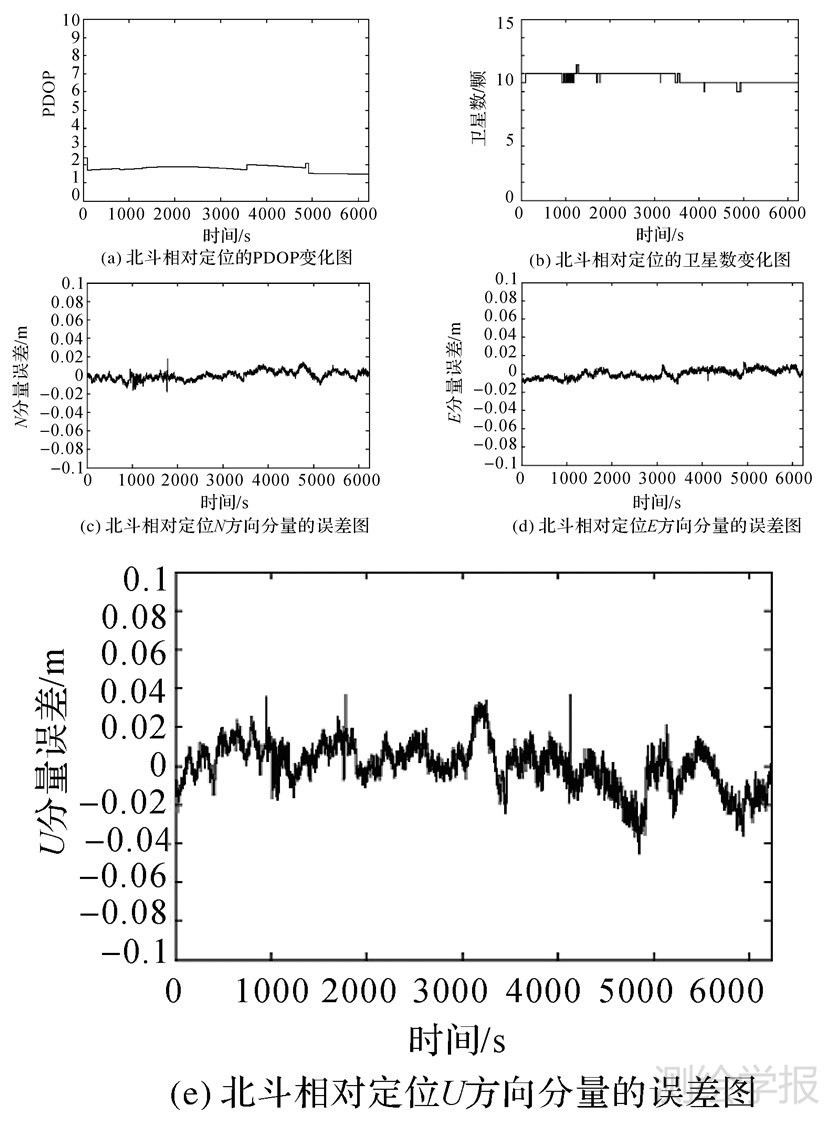
| 图 3 Fig. 3 |
从图 1中可以得出：GPS的PDOP值在2～4之间变化，卫星数在7～10之间，水平方向定位结果一般优于1 cm，垂直方向定位结果一般优于2 cm，在卫星数增加或减少时会出现个别较大的误差，一般为2 cm左右。
然后采用与GPS类似的方法对北斗数据进行处理，可得到北斗的定位结果，如图 2所示。由于北斗卫星数一直为5，所以PDOP变化比较平缓。由于目前北斗卫星数较少，并且分布不均匀，主要集中在东西方向上，所以北斗卫星的PDOP值整体都比较大，并且东西方向的定位精度明显高于其他方向，与GPS处于同一精度。由于卫星数比较稳定，东西方向精度甚至还稍优于GPS的；其他方向由于受卫星数和卫星分布的限制，稍差于GPS的。
最后采用上述方法对北斗和GPS数据进行联合定位解算，得到BeiDou/GPS的定位结果，如图 3所示。需要说明的是，北斗和GPS在联合解算时分配的是相同的权比，并且结果图中各轴含义和误差单位同前。从图 3中可以得出：BeiDou/GPS的卫星数明显多于单一卫星系统，PDOP值也有所下降，特别是GPS卫星数较少，分布较差时(如图中的4800 s附近)，定位精度也较单一系统有所提高。
(3) 为了便于定量分析比较，对上述3种情况下的每个分量误差进行概率统计，求出其均方根误差(RMS)，列于表 2中。| mm | |||
| N分量误差 | E分量误差 | U 分量误差 | |
| GPS | 6.5 | 7.0 | 12.9 |
| BeiDou | 9.9 | 3.1 | 18.5 |
| BeiDou/GPS | 4.5 | 4.5 | 11.7 |
我国的北斗卫星定位导航系统目前处于积极建设中，通过本文的论述与测试分析，可得如下结论：
(1) 北斗卫星导航系统已经具备我国范围内的初步三维高精度定位导航能力；
(2) 由于整个北斗系统尚未布设完成，现有卫星数量较少、几何分布较差，是造成单独北斗定位精度整体偏低的主要原因；
(3) 相同卫星条件下，北斗与GPS在高精度相对定位方面处于同一精度级别，二者联合定位可以明显增加可用卫星资源，改善卫星几何结构，提高卫星定位精度。
(4) 随着我国北斗系统的快速建设与不断完善，北斗定位将更加精确有效。
致 谢：感谢宁津生院士一直以来对笔者的指导与帮助，同时对宁院士的80华诞表示衷心的祝贺！| [1] | YANG Yuanxi. Progress, Contribution and Challenges of Compass/Beidou Satellite Navigation System [J]. Acta Geodaetica et Cartographica Sinica, 2010,39(1):1-6. (杨元喜.北斗卫星导航系统的进展、贡献与挑战[J].测绘学报,2010,39(1):1-6.) |
| [2] | CHEN Junyong, YANG Yuanxi, WANG Min, et al. Establishment of 2000 National Geodetic Control Network of China and It’s Technological Progress[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 1-8. (陈俊勇,杨元喜,王敏, 等.2000 国家大地控制网的构建和它的技术进步[J].测绘学报,2007, 36(1):1-8.) |
| [3] | CHENG Pengfei, WEN Hanjiang, CHENG Yingyan, et al. Parameters of the CGCS2000 Ellipsoid and Comparisons with GRS80 and WGS-84 [J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(3):189-194.(程鹏飞,文汉江,成英燕,等.2000国家大地坐标系椭球参数与GRS80和WGS-84的比较[J]. 测绘学报, 2009,38(3):189-194.) |
| [4] | YU Zhongchou, YU Zhenglin. Principle of Surveying Adjustment [M], Wuhan: Publishing House of Wuhan University of Surveying and Mapping, 1990. (於宗俦, 于正林. 测量平差原理[M]. 武汉: 武汉测绘科技大学出版社, 1990.) |
| [5] | QIN Yongyuan, ZHANG Hongcheng,WANG Shuhua. Principles of Kalman Filtering and Combination Navigation[M]. Xi’an: Northwestern Polytechnical University Press. 1998. (秦永元, 张洪铖,汪叔华. 卡尔曼滤波与组合导航原理[M]. 西安:西北工业大学出版社. 2007.) |
| [6] | GAO Xingwei, LIU Jingnan, GE Maorong. An Ambiguity Searching Method for Network RTK Baselines between Base Stations at Single Epoch [J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(4):305-309. (高星伟,刘经南,葛茂荣. 网络RTK基准站基线的单历元整周模糊度确定方法[J].测绘学报, 2002, 31(4):305-309.) |
| [7] | ZHU Huizhong, GAO Xingwei, XU Aigong, et al. Single Epoch Ambiguity Resolution for Network RTK Rovers [J]. Science of Surveying and Mapping, 2010, 35(2): 77-79. (祝会忠,高星伟,徐爱功,等. 网络RTK流动站整周模糊度的单历元解算[J].测绘科学,2010, 35(2):77-79.) |
| [8] | ZHU Huizhong, GAO Xingwei, BI Jinzhong, et al. An Algorithm of GPS Ambiguity Resolution on Single Epoch [J]. Science of Surveying and Mapping, 2011, 36(4): 9-11. (祝会忠,高星伟,秘金钟,等. 一种GPS整周模糊度单历元解算方法[J].测绘科学,2011, 36(4): 9-11.) |
| [9] | TEUNISSEN P J G. The Least Squares Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy,1995,70(1/2):65-82. |