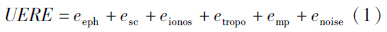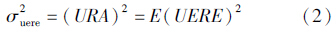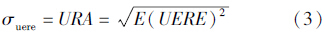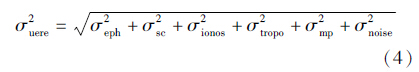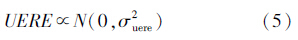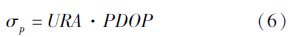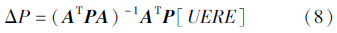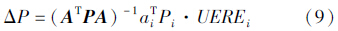2. 西安测绘研究所，陕西 西安 710054
2.Xi’an Institute of Surveying and Mapping，Xi’an 710054， China
1 卫星导航定位中的误差类型
卫星导航存在多种不确定性(误差)，如在时空基准方面，存在坐标系统误差和时间系统误差；在导航定位观测量方面，存在卫星轨道误差、卫星钟误差、电离层误差、对流层误差、多路径和热噪声等；在导航定位结果方面，存在位置误差、速度误差和时间误差等。依据误差的不同统计特性，这些误差可分为偶然误差、系统误差、异常误差、有色噪声等。
偶然误差(random error，又称随机误差)指的是由各类随机性因素引起的误差[1]，这类误差的个体呈现随机性，毫无规律，但统计上服从特定统计规律，如正态分布或重尾分布(Huber分布)等[2]。卫星测距误差、空间信号(signal in space)一般以随机误差为主。
系统误差(systematic error)指的是由某些特定因素的系统性影响而产生的具有某种规律的误差，如常量系统误差、周期性系统误差等。系统误差的影响具有累积性。如动力学模型误差[3, 4]卫星轨道误差、坐标系统误差、电离层延迟误差、对流层延迟误差等属于系统误差。
异常误差(outlier,blunder or gross error，又称粗差)指的是由设备异常、观测条件异常变化而引起的误差，一般以异常值、孤值或野值的形式表现出来。卫星轨道机动、卫星设备故障、接收机故障等引起的卫星测距误差或载波测量误差等超大误差属于异常误差。
有色噪声(colored error or colored noise)指的是随时间变化而有规律变化的误差[5]。有色噪声随时间变化而变化，时间越长有色噪声的影响一般越大。卫星导航一般采用动态模式，卫星本身在运动，用户也在运动，大气、环境也在随时间变化，于是相应随时间变化的大气误差、时钟误差、多路径误差等也可以归类为有色噪声。有色噪声一定是系统误差，而系统误差不一定是有色噪声，只有随时间变化的系统误差才是有色噪声。
卫星导航定位实践中，偶然误差与系统误差经常在不同场合互相转换。如测定卫星轨道时，卫星运行中受到多种摄动力的复杂影响，各种影响本身可能是系统性的，如地球重力场对卫星轨道的影响、大气阻力影响、太阳光压影响等，但这些影响综合在一起则可能削弱其规律性，而呈现出随机性误差特性。各类随机性的误差通过定轨数据处理后，可能剩余部分误差，这类误差对卫星导航定位用户而言则又变成了系统误差。在多卫星体系下，单个卫星轨道的系统误差在多系统融合导航定位时可能呈现出随机性，而变成用户的随机误差。
偶然误差与有色噪声经常发生相互转换。如单个卫星系统或时钟的有色噪声，在多系统融合时的个体规律性往往变成整体的无规律，而呈现随机性。多模卫星导航定位及有望补偿部分有色噪声的影响[6, 7, 8]。单一时刻的伪距随机误差，随着时间的变化也可能呈现出某种规律性，而变成有色噪声的特性。
导航实践中的系统误差与有色噪声之间更加难以区别。大多数系统误差在卫星导航领域均呈现有色噪声特性，即表现出随时间的变化而有规律地变化。如时钟误差本身是系统误差，但随着时间的推移这类误差在缓慢地变化，呈现出有色噪声特性。
2 卫星导航中常用误差度量关于误差度量的描述，不同的学者针对不同的问题可能会有不同的描述。在卫星导航领域常用的误差度量有“精度”(precision)、“精确度”(accuracy)、“可靠性”(reliability)[9]和“不确定性”(uncertainty)等。
2.1 不确定性与不确定度本文将不确定性与不确定度作严格区分。不确定性(uncertainty)是不精确性、模糊性、不明确性等概念总称[10]，不确定度(uncertainty measure)应作为不确定性的度量。导航定位的不确定性指的是各类与卫星动力学、卫星载荷、信号传播、地面接收机等相关的误差，甚至包括卫星导航政策的不确定性；导航定位的不确定度指的是与导航定位结果相联系的指标参数，表征导航定位输出结果的分散性。
不确定性分为A类标准不确定性，B类标准不确定性，合成标准不确定性和扩展不确定性[11]。相应地，也应该有相应的不确定度与之对应。
在导航领域，A类不确定度一般用导航定位参数或其他观测量的离散度的统计值进行度量，用方差或标准差(或中误差)表示。A类不确定度一般只能度量随机误差。
B类不确定度一般基于导航接收机设备、卫星轨道、大气延迟、导航模式、设备检定证书标定指标等信息以及经验进行综合评定，一般也用统计的标准差(或中误差)表示。显然，B类不确定度与A类不确定度只是在评定方法上有差别。当然这种差别有时会带来概念上的差别。如果设备证书或设备检验结果标定某类设备存在系统误差，则在B类不确定性度量时可以估计这些系统误差，而A类不确定度只是基于实际观测本身的离散度，不涉及系统误差的度量。
合成标准不确定度描述的是合成不确定性度量。将合成不确定性构造成特定的函数关系，由误差传播定律求得合成不确定性的不确定度，可以用方差、均方差或中误差表示。
扩展不确定度是指确定导航定位结果的量值区间，即导航定位结果按一定概率落入的特定区间，这类不确定度估计也可称为误差区间估计。如某导航定位值为x，相应的标准差为σx，假设误差服从正态分布，则x的扩展不确定度为[x-kσxx+kσx]，若取k=2，则相应概率为95.45%；若k=3，相应概率为99.73%[12]。扩展不确定度也可用误差椭圆或误差椭球表示[13]，对于多维情形，甚至可以采用超误差椭球表示。
2.2 精度与精确度由于比对基准的不同，精度可分为内部精度和外部符合精度。内部精度以估计的最或然估值为比对基准，主要反映了观测值之间的离散度，即精密度(precision)，一般用中误差(standard deviation)来度量。外部符合精度以外部提供的参考值为比对基准，主要反映了观测值与参考值的偏差程度，即为精确度(accuracy)，一般用误差的均方根(root mean square of errors，RMS)度量。方差(variance)是中误差或均方根的平方。
设有n个观测组成向量L，真误差向量Δ，残差向量V，则均方差σ的估计值一般用中误差m计算[1]，
；若用残差表示，则中误差的最小二乘估计值为
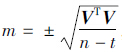，其中，t为模型参数个数;n-t为多余观测个数。上述两种表示形式的平方所表示的方差的估计值均满足无偏性，且可以严格推导出来。
用残差表示的中误差估计式一般只反映观测内部“精度”，不反映观测系统误差，不能作为“精确度”指标。有时尽管存在明显的系统误差，但观测的离散度仍然很低，即中误差依然很小，反映表面精度较高。
精确度(accuracy)反映观测或参数估计的实际可信度，反映导航定位估计值与真值的偏差程度。关于精确度的计算，不同参考值有不同的计算方法。例如，在t1、t2…tn时刻，由精密单点定位解得两IGS站点间的基线长度估计值为S1、S2…Sn，由长期连续观测站解得的基线长度参考值为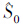
，求得差值(或不符值)
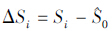，则精确度可用不符值的均方根RMS表示，即RMS=
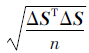，其中，ΔS=[ΔS1 ΔS2 … ΔSn]T。又例如，相同的t维参数向量X，在不同时刻采用相同的手段解得两组参数估计值向量
和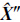
，并求得不符值向量为
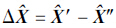，则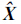
向量的精确度可表示为RMS=
。
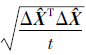精确度能较可靠地反映导航信号或导航解的偶然误差、系统误差及异常误差的总体影响。实际上用真误差表示的中误差与RMS具有相同的特性，都可作为“精确度”指标。注意区别于以残差表示的中误差。
3 用户距离误差与用户距离精度在卫星导航领域，常用的“用户测距误差”(user range error，URE)和用户等价测距误差(user equivalent range error，UERE)[14]是由多种因素影响的综合误差，前者定义为卫星星历拟合误差到用户距离的投影[15]，包括卫星星历误差eeph、卫星钟误差esc；后者除卫星星历误差外，还包括电离层延迟误差eionos、对流层延迟误差etropos、多路径误差emp、接收机噪声enoise等，这类合成误差的集合可以看成是合成不确定性。
用公式表示为
注意式(1)表示的用户等价距离误差(UERE)是各类距离测量不确定性的代数和，在应用GNSS导航进行导航定位过程中，各类信号传播误差对用户距离的影响正是以这种代数和的形式影响最终的用户距离观测。
根据用户距离误差可定义用户距离精度(user range accuracy，URA)
或写成均方差形式 即用户距离精度为用户距离均方差。
假设用户等价距离误差表达式(1)中各不确定性分量的期望值为零且不相关，并令E(e2i)=σ2i，则用户距离不确定度或用户距离精度可表示为
如果用户距离误差服从期望为0的正态分布，则可将其表示成 显然，UERE与σ2uere总是相对应的。
注意，在有些文献上，将式(4)称为用户等价距离误差UERE[15]，笔者认为将式(4)称为UERE是不合适的。
利用URA可以确定定位精度，如点位精度可表示为
式中，PDOP为点位精度衰减因子
而Qx为点位坐标的协因数矩阵。
注意将点位精度或点位误差表示成如下公式都是不正确的
EPE=UERE×GDOP
若讨论点位误差影响ΔP，则有
式中，[UERE]=[UERE1 UERE2 … UEREn]T。若讨论其中一个距离误差对用户定位精度的影响，则有
式(4)表示的是用户等价距离精度的理论表达式，实际估算时还可以根据用户距离观测的离散度进行计算。
用户等价距离误差的另一种表示形式为[11]
这种表示形式是目前大多数GNSS教科书中常见的表示形式，如果各误差分量直交，则式(10)表示的是n维空间误差对点位影响的距离，或称为观测不确定性导致的点位偏差。若各误差轴向不互相直交的话，则式(10)是表示的UERE是不合适的。在三维情形下，如果3个坐标误差分量分别是ex、ey、ez，由于x、y、z轴互相直交，则点位误差ΔP为
将式(10)表示成
等式两端取数学期望，则同样可以得到式(4)表示的用户距离精度。
URA标定特定信号情况下能获得的GNSS用户距离精度统计值。URA提供了保守的UERE的误差均方根RMS(root mean square)估计，URA也是完好性阈值确定的基础。
笔者认为目前卫星导航界采用的URE或UERE定义并不合适，容易将误差与精度指标相混淆。
4 几点注记注记1：不确定性与误差意义相近，但不确定性涵盖内容更广，如属性不确定性、模糊不确定性等。误差一般可以用数值表示，不确定性有时不能用数值表示。
注记2：不确定性与不确定度有区别，不确定度是不确定性的度量。不确定度与测量界的精度度量方式几乎完全一致，所有不确定度均可以用方差、均方差、误差区间、误差椭圆、误差椭球表示。
注记3：A类不确定度与B类不确定度都采用均方差或标准差度量，只是度量方法不同，前者用直接观测的离散度度量，后者采用经验值、设备的标定精度、以往的测量精度、经验分布等信息进行度量。显然，A类不确定度只能估计观测量的离散度，而B类不确定度可估计观测结果的随机误差和系统误差的离散度，只要设备检定、产品说明书、甚至以往观测经验已经表明观测存在可度量的系统误差。
合成不确定度(C类)一般采用方差-协方差传播定律求得随机变量函数的方差或均方差，然后再表示成用户需要的误差区间或误差椭圆等。扩展不确定度与测量界的误差区间估计几乎一致，均基于变量的期望和相应的均方差及其误差分布进行度量。
注记4：导航界与测量界经常把中误差与RMS相混淆，前者反映内部精度，一般由变量的残差表示；后者反映精确度，一般以重复误差或称不符值(真误差)表示。
注记5：导航领域的用户距离误差(URE)和用户等价距离误差(UERE)实际与不确定性概念一致，都属于合成误差，相应的用户距离精度(URA)可以通过方差协方差传播定律求得。
注记6：用户距离精度除可以用误差传播定律得到理论表达式外，也可以用实际用户距离观测的离散度进行估计，如采用RMS或用距离观测残差表示的均方差表达式估计。
注记7：导航界经常将“用户距离误差”与“用户距离精度”相混淆，在表示用户距离误差时可以标定1倍均方差、2倍均方差或3倍均方差，也可以用概率表示误差落入某区间的概率，如标定URE不大于10 m(95%)，这说明95%的用户距离误差都落在[-10 m，10 m]范围内，且观测标准差或用户距离精度为5 m；但在标定用户距离精度时，不应再标定2倍或3倍均方差，也不应再标定概率，因为用户距离精度(均方差)本身就是全部误差的统计值。
| [1] | 隋立芬,宋力杰,柴洪洲.误差理论与测量平差基础[M].北京:测绘出版社,2010.(SUI Lifen,SONG Lijie,CHAI Hongzhou.Error Theory and Surveying Adjustment[M].Beijing:Surveying and Mapping Press,2010.) |
| [2] | 杨元喜.抗差估计理论及其应用[M].北京:八一出版社,1993.(YANG Yuanxi.Robust Estimation Theory and Its Applications[M].Beijing:Bayi Publishing House,1993.) |
| [3] | 杨元喜.动态Kalman滤波模型误差的影响[J].测绘科学,2006,31(1):17-18.(YANG Yuanxi.Model Error Influences on Kalman Filtering[J].Journal of Surveying and Mapping Science,2006,31(1):17-18.) |
| [4] | 高为广,杨元喜,张双成.顾及动力学模型误差影响的GPS/INS组合导航自适应滤波算法[J].武汉大学学报:信息科学版,2008,33(2):191-194.(GAO Weiguang,YANG Yuanxi,ZHANG Suangcheng.GPS/INS Adaptive Filtering Considering the Influences of Kinematic Model Errors[J].Geomatics and Information Science of Wuhan University,2008,33(2):191-194.) |
| [5] | 赵长胜.有色噪声滤波理论与算法[M].北京:测绘出版社,2011.(CHAO Changsheng.Filtering Theory and Algorithms with Colored Noises.Press of Surveying and Mapping[M].Beijing:Surveying and Mapping Press,2011.) |
| [6] | 杨元喜.北斗卫星导航系统的进展、贡献与挑战[J].测绘学报,2010,39(1):1-6.(YANG Yuanxi.Review on Progress,Contribution and Challenges of Beidou Satellite Navigation System[J].Acta Geodaetica et Cartographica Sinica,2010,39(1):1-6.) |
| [7] | YANG Y X,LI J L,XU Y J,et al.Generalized DOPs with Consideration of the Influence Function of Signal-in-Space Errors[J].The Journal of Navigation,2011,64(S):3-18. |
| [8] | YANG Yuanxi,LI Jinlong,XU YiJun,et al.Contribution of the Compass Satellite Navigation System to Global PNT Users.Chinese Science Bulletin,2011,Vol.56 No.26,2813-2819.(杨元喜,李金龙,徐毅君,等.中国北斗卫星导航系统对全球PNT用户的贡献[J].科学通报,2011,56(21):1734-1740.) |
| [9] | 王金铃、陈永奇.论观测的可靠性度量[J].测绘学报,1994,23(4):252-258.(WANG Jinling,CHEN Yongqi.Some Remarks on the Reliability Measures[J].Acta Geodaetica et Cartographica Sinica,23,252-258.) |
| [10] | SHI W Z.Principles of Modeling Uncertainties in Spatial Data and Spatial Analyses[M].Hong Kong:CRC Press,2010. |
| [11] | 许自富、刘东、阮安路.不确定度、准确度、精度辨析[J].计量技术,2007,27(2):37-39.(XU Zifu,LIU Dong,RUAN Anlu.Review on Uncertainty Measure,Accuracy and Precision[J].Measuring Technology,2007,27(2):37-39.) |
| [12] | KOCH K R.Parameter Estimation and Hypothesis Testing in Linear Models[M].2nd ed.Berlin:Springer,1999. |
| [13] | 杨元喜.关于"新的点位误差度量"的讨论[J].测绘学报,2009,38(3):280-282.(YANG Yuanxi.Discussion on "New Measure of Optional Error" [J].(Acta Geodaetica et Cartographica Sinica,2009,38(3):280-282.) |
| [14] | MONHINDER S G,LAWRENCE R W,ANGUS P A.Global Positioning Systems,Inertial Navigation and Integration[M].New York:Wiley&Sons,2001. |
| [15] | KUUSNIEMI H.User-level Reliability and Quality Monitoring in Satellite-based Personal Navigation[R].Tampere:Tampere University of Technology.2005. |
| [16] | 李德仁.误差处理和可靠性理论[M].北京:测绘出版社,1988.(LI Deren.Error Processing and Reliability Theory[M].Beijing:Surveying and Mapping Press,1988.) |
| [17] | 周江文、杨元喜.论余差及杠杆观测[C]//抗差估计论文集,北京:测绘出版社,1992.(ZHOU Jiangwen,YANG Yuanxi.On Residuals and Leverage Observations[C]//Collection of Robust Estimation,Beijing:Surveying and Mapping Press,1992.) |