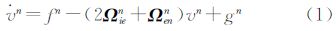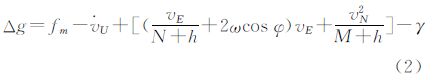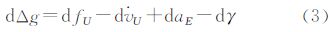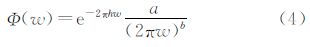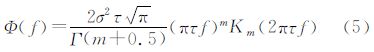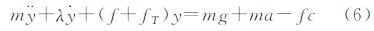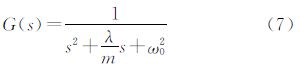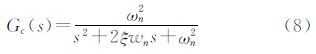2. 中国科学院大学,北京100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
1 引 言
航空重力测量是一种高效经济的重力测量方式,能够在各种地形条件下快速获取高精度、高分辨率以及一致性好的重力场数据,在资源勘探、军事、大地测量与地球物理等领域的应用越来越广泛,我国的航空重力测量也正在不断发展中。由于测量噪声以及重力场随高度衰减的特性,航空重力测量仅能恢复一定频段内的重力场信息。因此,对航空重力测量系统的两大组成部分重力仪及GPS的误差进行时域、频域分析,确定系统工作频带、分析重力仪响应的影响因素,对于重力测量系统研制有着重要意义。文献[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]分别利用误差功率谱密度(power spectral density,PSD)分析了航空矢量重力测量系统、重力梯度测量系统的频域响应;利用重力场阶方差函数结合L&R重力仪分析了航空重力理论恢复阶数;对CHZ重力仪的航空应用进行了初步讨论。
CHZ重力仪由中国科学院测量与地球物理研究所于20世纪80年代末研制成功。该仪器采用轴对称式机械结构,并应用垂直悬挂零长弹簧秤作为重力传感系统,加入硅油阻尼和恒温控制,有效地消除了交叉耦合效应和非线性误差的影响,是目前技术思想先进的海洋重力仪。CHZ型海洋重力仪先后进行了数千海里测线的比对测量,表明其在恶劣海况时的动态测量精度可达到1 mGal(1 mGal=10-5 m/s2)。20世纪90年代,CHZ型海洋重力仪先后两次在国产Z-8直升机上进行了我国早期的航空重力测量试验,表明其动态性能符合航空重力测量要求[12, 13]。由于当时条件限制,该型仪器未能在固定翼飞机上进行测试。因此,有必要分析CHZ重力仪在固定翼条件下的动态性能,为固定翼CHZ航空重力系统的研制提供参数。
本文首先分析航空重力测量系统在不同高度恢复重力场的能力,给出频谱窗口并分析了影响因素。其次,利用实测的空中重力异常数据及机载GPS动态加速度数据作为CHZ重力仪运动方程的输入,对CHZ重力仪的阻尼系数、时间响应等动态性能进行研究。
2 航空重力测量的理论基础航空重力测量的基本原理为牛顿第二运动定律,通常采用其在当地水平坐标系下的形式[1, 2, 6, 7]
式中,v、 n分别为载体速度、加速度,由GPS确定;fn为当地水平坐标系下的比力观测值;Ωie、Ωen分别为ωie、ωen(坐标系的旋转角速度矢量)的反对称矩阵;g为重力加速度矢量。其中,上标n表示当地水平坐标系。
n分别为载体速度、加速度,由GPS确定;fn为当地水平坐标系下的比力观测值;Ωie、Ωen分别为ωie、ωen(坐标系的旋转角速度矢量)的反对称矩阵;g为重力加速度矢量。其中,上标n表示当地水平坐标系。
对于航空标量重力测量而言,其原理为式(1)的垂直分量,即
式中,下标E、N、U分别表示当地水平坐标系的东、北、天方向;ω为地球自转角速度;φ为地理纬度;h为大地高;M、N分别为椭球子午圈、卯酉圈曲率半径;Δg、γ分别为重力异常及飞行高度处的正常重力;括号中为厄特弗斯项,用aE表示;fm为比力测量值。航空标量重力测量中通常采用两轴阻尼平台为传感器提供垂直基准,但是该平台在飞机有水平加速度的情况下会产生倾斜,由此对重力仪观测值产生的影响即为水平加速度改正aH。顾及水平加速度改正,则式(2)中的比力观测值定义为fU。
对式(1)求全微分,则其误差方程
根据文献[1, 14]直接给出dfU=dfm-axα-alβ+g/2(∂α2+β2),其中,dfm为重力传感器测量误差,ax、al为平台水平加速度;α、β分别为两个水平方向的倾斜角。后3项即为平台非水平所引起的重力测量误差,来自于平台倾斜角与加速度值的耦合。考虑到阻尼平台的两个水平轴特性一致,为简化运算,假设α、β,ax、al分别相等,则dfU=dfm-2axα+gα2。
为了分析航空重力测量系统误差功率谱,根据功率谱密度的运算法则,其误差功率谱即为误差方程各误差项功率谱之和,Pdδg=Pdfm+P2axα+Pgα2+Pd u+PdaE+Pdγ,下节将分别计算误差功率谱密度[1, 4, 5, 9, 10, 14]。
u+PdaE+Pdγ,下节将分别计算误差功率谱密度[1, 4, 5, 9, 10, 14]。
航空重力测量恢复重力场的频带范围可以通过比较外空重力场、航空重力测量系统噪声的功率谱密度确定,重力场信号功率谱大于测量噪声功率谱的频带即为可恢复重力场的范围。同时,可以分析影响频带范围误差来源[5, 9, 10]。
3.1 外空重力场的功率谱计算重力场能量通常随高度衰减,外空重力场的频谱特性是分析航空重力测量系统性能的基础之一。国内外的学者曾对外空重力场的频谱特性进行了大量的研究,文献[5]利用3个区域的重力异常数据,采用二维傅里叶变换计算得到了不同地形的重力异常PSD模型。文献[9, 10]利用EGM96模型及部分中等山区的1′×1′的平均重力异常以及30″×30″、1″×1″的地形数据,采用自协方差函数计算得到了相应的重力异常PSD模型。文献[8]利用我国部分重力异常数据得到了重力场高阶的阶方差模型,并分析了不同高度下外空重力场的传播特性。文献[11]利用全球13个不同区域的重力异常数据,采用二维傅里叶变换以及自协方差函数分别计算了这些区域的重力异常PSD,并拟合得到了去除地形影响的重力异常PSD模型。本文采用了该模型并利用向上延拓公式得到不同高度的重力异常PSD模型
式中,a=5.2 mGal2/kmb-2;b=4.09;h、w分别为高度及空间频率。
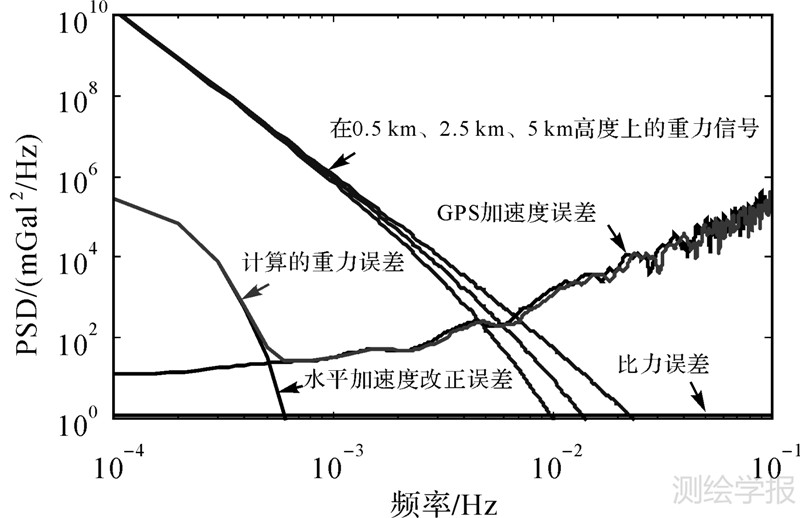
为研究方便,通常将上式中的空间频率乘以飞行速度转换为时间频率Hz,本文计算取飞行速度为300 km/hr,向上延拓高度分别为0.5 km、2.5 km、5 km。图 1中蓝线自上而下分别为0.5 km、2.5 km、5 km情况下的PSD。
|
| 图 1 重力异常以及航空重力测量系统误差功率谱 Fig. 1 The PSD of gravity anomalies and airborne gravimetry errors |
由上节可知,航空重力测量的误差主要来源于载体加速度、重力传感器,其误差功率谱可以由这两部分的误差功率谱相加计算得到。
首先,计算载体加速度误差功率谱。在航空重力测量中,载体加速度可由GPS确定的载体位置经过两次微分计算得到。载体加速度的真值是未知的,因此,其误差只能通过间接方法估计,如通过重复测线或者多地面站分别推求的载体加速度相减得到。本文使用的GPS数据来源于某次航空重力测量[6, 7],包含了两个地面参考站、一个移动站的数据,数据分辨率为1 Hz,分别计算了两个地面站各自差分得到的载体位置,微分计算得到两组加速度值,将两组加速度值相减计算得到载体加速度误差[16, 17, 18, 19, 20, 21, 22]。再利用自相关函数法估计得到加速度误差序列的功率谱,见图 1。
其次,计算重力传感器误差功率谱。文献[9, 10]利用傅里叶变换结合协方差函数给出了根据标准差计算PSD的解析公式,并利用此模型研究了INS矢量重力传感器的误差功率谱。本文采用了该解析式,具体为式(5),该模型需给定传感器误差的标准差
式中,σ为传感器误差的标准差;τ为相关时间,其与数据采样频率有关,本文采用的为1 s;Γ为欧拉伽马函数;Km为第二类贝塞尔函数,m为贝塞尔函数的次,为保证计算的功率谱总是为正,文献[10]给出的m通常取为10。
航空重力测量中比力测量、厄特弗斯改正、正常重力的误差表现为随机白噪声。在本文的计算中,根据目前重力传感器的设计指标,比力测量的标准差取0.2 mGal。厄特弗斯改正的精度主要取决于载体速度的精度,目前测速精度优于0.03 m/s,厄特弗斯的精度可以优于0.5 mGal。而正常重力的计算精度取决于定位精度,计算精度为0.01 mGal。水平加速度改正的量级与水平加速度大小相关,文献[1, 14]分析了平台非水平角与水平加速度的关系,本文采用水平加速度为2000 mGal,相应的平台非水平角为0.002 rad[9, 10, 14],水平加速度改正的误差PSD示于图 1。
由图 1可知,比力测量等误差影响量级非常小;在低频段内,平台非水平角带来的误差占据主要影响,约为2 mGal,对于提高系统精度影响较大,须事后处理改正。GPS加速度误差随着频率的增加而快速的增大,是航空重力误差来源的主要部分。文献[1, 2]从频域分析了影响GPS载体加速度精度的因素,在大于0.005 Hz的频段上,加速度误差主要来源于多路径效应及测量噪声。由图可知,航空标量重力在0.5 km、2.5 km、5 km飞行高度上对应的频谱截止范围分别为0.008 Hz、0.006 Hz、0.005 Hz。由于本文使用了经地形改正后的重力PSD模型,因此重力异常PSD值偏小,如果考虑地形因素则频谱窗口将会相应的增大,约为0.01 Hz,与文献报道一致[5, 9, 10, 16]。另外,根据式(4)也可知,降低飞行速度,频谱范围也会明显增大。由上分析可知,在实际测量中,降低飞行高度及飞行速度,都可以不同程度地提高航空重力测量恢复重力场的能力,制约频谱窗口提高的最重要因素仍然为载体加速度误差。
4 CHZ重力传感器的航空应用分析由于飞机速度较快,重力传感器的航空应用要求系统的时间响应尽可能小,以减小变形和滞后的影响。本节利用航空重力测量的频谱范围作为CHZ重力传感器工作带宽的约束,分析不同阻尼情况下重力传感器的动态性能。
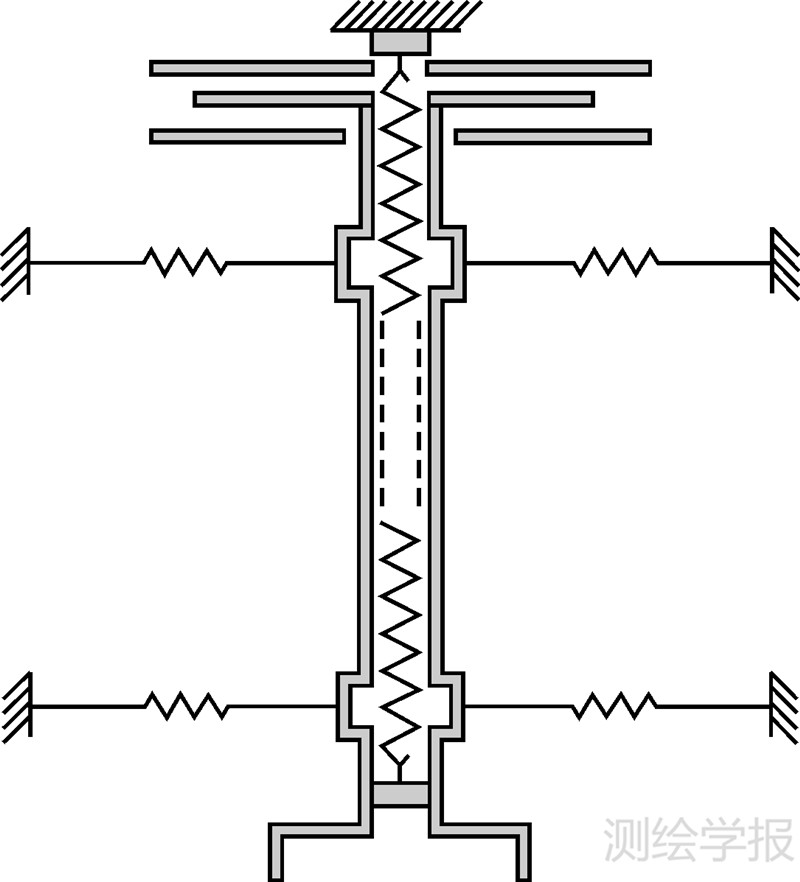
4.1 CHZ重力传感器结构及原理CHZ重力传感器实质是一个垂直弹簧秤,由一根弹性系数为f的垂直主弹簧和一个管状质量组成,其质量为m,并且利用弹性系数为fT的拉丝以及绷紧弹簧使管状质量在垂直方向上作无摩擦运动,整个传感器系统浸泡于阻尼系数为λ的硅油中。重力加速度主要部分由主弹簧拉力fc补偿,悬挂质量在静止时处于零位,c为静止时弹簧伸长。当重力发生变化时,弹簧将产生微小位移y,电容测微器检测后将位移转换为电量并送到比例积分放大器及比例积分线圈以补偿重力变化,利用电磁反馈将悬挂质量回复到零位。积分线圈上的补偿电流即为所测重力变化值[12, 13, 23, 24],如图 2所示。
|
| 图 2 CHZ重力仪原理 Fig. 2 The principal of CHZ gravimeter |
弹性系统动态时的运动方程为
ω02=(f+fT)/m,ω0 称为系统的固有频率。
从式(6)可以看出,动态重力仪不仅敏感重力加速度g而且也敏感载体运动加速度a,因此必须采用一定的手段将重力加速度与载体运动加速度进行分离。在海洋重力测量中,根据海浪产生的垂直加速度周期短的特点,CHZ海洋重力仪利用强硅油阻尼和电磁滤波即可将垂直加速度从重力仪读数中完全排除。而航空重力测量中,飞机所产生的垂直加速度要比海洋重力复杂的多,其噪声的频谱范围较之海洋重力要宽许多,采用强阻尼是无法完全去除垂直加速度影响。同时,强阻尼将会使得重力测量产生严重的幅度衰减与相位滞后,航空重力测量的飞行速度通常在每小时上百公里,这将对重力测量分辨率的提高产生影响。目前的航空重力测量系统中,除使用阻尼消除部分频段的垂直加速度外,另外需使用GPS确定载体加速度并结合滤波后处理去除垂直加速度影响。
CHZ重力传感器是一个典型的二阶系统运动方程,其中弹性系统固有频率ω0是确定的,阻尼系数λ的不同选择是系统性能的关键影响因素。因此,有必要针对航空重力测量的特点,探讨CHZ重力传感器阻尼系数的范围。
一般通过求解微分方程或者传递函数来研究系统性能,本文采用传递函数来进行分析[25]。针对式(6),传递函数为
利用此传递函数可计算得到弹性系统由外部输入信号引起的弹性位移量,其中s为复数变量。
CHZ重力传感器信号处理包含了弹性系统、测微系统、比例反馈、积分平均、积分反馈系统,通过这一系列的系统工作即可得到重力仪输出。重力传感器系统的闭环传递函数为
式中,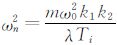 ;
;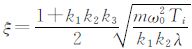 ,对于二阶闭环系统而言,
,对于二阶闭环系统而言,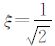 是最佳设计系数,在此情况下,可以确定出系统的积分时间Ti,且ωn即为系统的截止频率(带宽),其与阻尼系数成反比。
是最佳设计系数,在此情况下,可以确定出系统的积分时间Ti,且ωn即为系统的截止频率(带宽),其与阻尼系数成反比。
上述两个传递函数中,m=0.03 kg、ω0=10、k1k2=3.247 2 mV/mGal、k3=10是由CHZ重力传感器及电路设计参数得到,阻尼系数λ是可调整的,以此为基础分析CHZ重力传感器的航空环境下的性能。根据上节中确定的航空重力频谱窗口0.01 Hz,由式(8)计算得到系统最大阻尼系数约为8000。
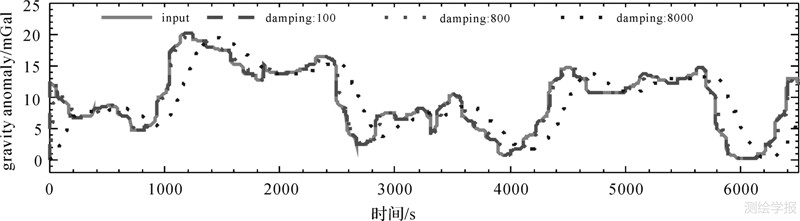
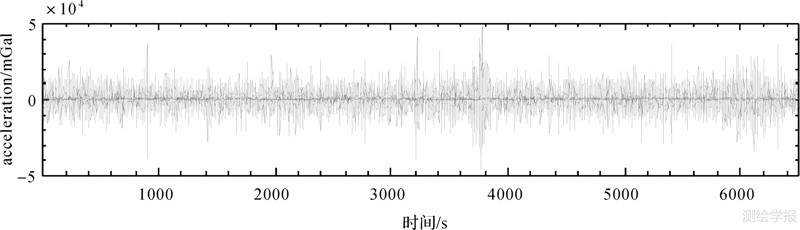
4.2 计算分析本节使用实测的飞机加速度数据以及空中的重力异常数据作为CHZ重力传感器输入,根据重力仪传递函数的输出,分析CHZ重力传感器航空应用的性能。输入数据来源于某航空重力测量,飞机加速度数据由GPS确定,采样率为1 Hz,飞行高度1000 m,空中重力异常数据由地面重力数据经向上延拓获得[1, 19, 20, 21, 22],在图 3、图 4中以灰色标注。
|
| 图 3 CHZ重力测量系统对重力异常的响应 Fig. 3 The response of Gravity anomalies through CHZ gravimeter |
|
| 图 4 CHZ重力测量系统对垂直加速度的响应 Fig. 4 The response of vertical acceleration through CHZ gravimeter |
利用式(8)计算得到不同阻尼情况下的重力仪输出。为了便于分析,将重力异常、垂直加速度的输出响应分别作图 3、图 4。
利用式(7)、式(8)分别计算得到不同阻尼情况下由上述输入所引起的弹性系统的位移及延迟时间,将最大位移、最小位移以及延迟时间统计于表 1。
| 测线 | 结果 | 10 | 100 | 800 | 2000 | 4000 |
| WE | 最大位移/μm | 2 813.5 | 356.64 | 44.65 | 18.212 | 4.524 2 |
| 最小位移/μm | 0.025 29 | 0.007 71 | 0.005 67 | 0.000 60 | 0.000 21 | |
| 延迟时间/s | 0 | 5 | 35 | 80 | 120 | |
| NS | 最大位移/μm | 2 788.3 | 301.53 | 41.769 | 17.667 | 4.899 1 |
| 最小位移/μm | 0.034 986 | 0.006 19 | 0.003 33 | 0.000 39 | 0.000 24 | |
| 延迟时间/s | 0 | 3 | 20 | 70 | 100 |
由图 3、图 4中的原始输入数据可知,垂直加速度幅值是重力异常幅值的上千倍。随着阻尼系数的增大,垂直加速度压缩程度也大幅提高。根据阻尼系数800、2000、8000计算的垂直加速度与原始垂直加速度序列比较后发现,其幅值压缩平均为1/3、1/100、1/1000。随着阻尼系数的增大,重力异常的输出响应有了明显的时间延迟,但是幅值基本没有变化。但当采用阻尼系数8000时,幅值有所压缩,这也表明对应于阻尼系数8000的重力传感器系统带宽0.01 Hz已经接近了航空重力的频谱窗口,也证明了上节中给定的航空重力频谱窗口是有效的。
CHZ重力传感器测微系统设计指标为分辨率为10-3 μm,量程为103 μm。从表 1中可以看出,当阻尼系数采用10时,两条测线分别计算的位移量最大值超出了量程范围,采用阻尼系数2000时,两条测线最小位移值已经接近分辨率极限。另外,从阻尼系数分别对应的时间延迟来看,如果飞机以300 km/h飞行,阻尼系数2000对应的半波长分辨率为6 km,这对于提高航空重力分辨率影响非常大。
另外,本文采用的数据来自于中等湍流飞行环境,考虑到CHZ重力仪需要适应不同的测量环境,阻尼系数也需要适当加大。综合考虑飞行环境、弹性系统位移输出量级以及重力传感器输出的时间偏移,针对航空重力应用的CHZ重力传感器阻尼系数在800左右是适宜的,既能对垂直加速度幅度进行有效压缩,同时时间延迟也满足航空重力测量的要求。
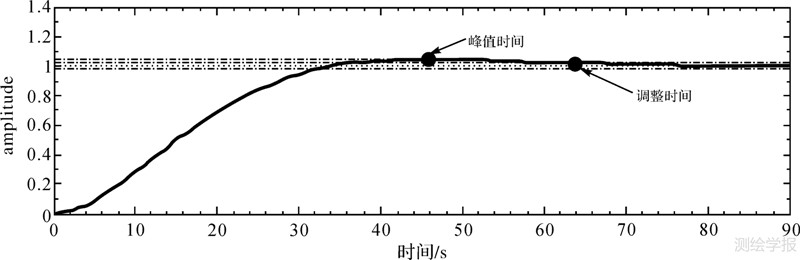
在控制系统理论中,通常利用单位阶跃输入来判断系统的瞬态响应性能,进而判断其稳定性,阻尼系数采用800时,重力传感器系统的单位阶跃响应见图 5。从单位阶跃响应图可知,在阻尼系数为800时,系统调整时间约为63.8 s,CHZ重力传感器系统是稳定的。
|
| 图 5 CHZ重力仪单位阶跃响应 Fig. 5 The step response of CHZ gravimeter |
航空重力测量误差的频域分析表明,航空标量重力的频谱截止范围约为0.01 Hz。稳定平台非水平误差影响集中于低频段,制约了航空重力测量精度的提高,此项须经事后改正。制约频谱窗口提高的最重要因素为载体加速度误差,提高载体加速度确定精度对于改善航空重力测量分辨率仍然有着重要意义。同时,本文介绍的航空重力测量频谱窗口的确定方法及结论也可以应用于其他原理的航空重力仪研制中。
通过分析CHZ重力传感器运动方程在不同阻尼系数条件下对实测空中重力异常与GPS载体加速度数据的输出响应,本文认为综合考虑飞行环境、弹性系统位移输出量级以及重力传感器输出的时间偏移,CHZ重力传感器阻尼系数在800左右是适宜的,既能对垂直加速度幅度进行有效压缩,其时间延迟也满足航空重力测量的要求。这同时表明,CHZ重力仪能够被用于固定翼飞机的航空重力测量。
| [1] | SUN Zhongmiao. Theory, Methods and Applications of Airborne Gravimetry[D]. Zhengzhou: Information Engineering University, 2004. (孙中苗.航空重力测量理论、方法及应用研究[D]. 郑州:信息工程大学, 2004.) |
| [2] | BRUTON A M. Improving the Accuracy and Resolution of SINS/GPS Airborne Gravimetry[D]. Calgary: University of Calgary, 2001. |
| [3] | OLESEN A V. Improved Airborne Scalar Gravimetry for Regional Gravity Field Mapping and Geoid Determination [D]. Copenhagen: University of Copenhagen, 2002. |
| [4] | OLSEN A V, FORSBERG R, KELLER K. Error Sources in Airborne Gravimetry Employing a Spring Type Gravimeter[C]//IAG Symposium 125: Vistas for Geodesy in the New Millennium. Berlin: Springer Verlag, 2002: 205-210. |
| [5] | SCHWARZ K P, LI Y C, WEI M. The Spectral Window for Airborne Gravity and Geoid Determination[C]//Proceedings of the International Symposium on Kinematic Systems in Geodesy, Geomatics and Navigation. Calgary: University of Calgary, 1994: 445-456. |
| [6] | HWANG C, HSIAO Y S, SHIH H C, et al. Geodetic and Geophysical Results from a Taiwan Airborne Gravity Survey: Data Reduction and Accuracy Assessment[J]. Journal of Geophysical Research, 2007, 112(B4): 407-413. |
| [7] | HWANG C, HSIAO Y S, SHIH H C. Data Reduction in Scalar Airborne Gravimetry: Theory, Software and Case Study[J]. Computer & Geoscience, 2006, 32(10):1573-1584. |
| [8] | XIA Zheren, SHENG Zongqi, LI Yingchun. Propagation Properties of Disturbing Gravity Field Outside the Earth[J]. Chinese Journal of Geophysics, 1998, 41(4): 484-493. (夏哲仁, 盛宗琪, 李迎春. 外空扰动引力场的传播特性[J]. 地球物理学报, 1998, 41(4): 484-493.) |
| [9] | JEKELI C. Airborne Gradiometry Error Analysis[J]. Surveys in Geophysics, 2006, 27(2): 257-275. |
| [10] | JEKELI C. Statistical Analysis of Moving-base Gravimetry and Gravity Gradiometry: 466[R]. Athens: Ohio University, 2003. |
| [11] | JAKOB F. Short-wavelength Spectral Properties of the Gravity Field from a Range of Regional Data Sets[J]. Journal of Geodesy, 2006, 79(10): 624-640. |
| [12] | ZHANG Shanyan, ZHOU Dongmin, ZONG Jie, et al. Test of an Airborne Gravimeter[J]. Acta Geophysica Sinica, 1990, 33(1): 70-76. (张善言, 周东明, 宗杰, 等. 航空重力仪的试验[J]. 地球物理学报, 1990, 33(1): 70-76). |
| [13] | ZHANG Shanyan. Several Distinguishing Features of the CHZ Sea Gravimeter[C]//Acta Geodaetica et Geophysica: 12. Beijing: Science Press, 1991: 93-102. (张善言. CHZ海洋重力仪的若干特点[C]// 1990年中国地球物理学会第六届学术年会论文集. 北京:科学出版社, 1991: 93-102.) |
| [14] | PETERS M F, BROZENA J M. Methods for Improving Existing Shipboard Gravimeters for Airborne Gravimetry[C]//Proceedings of the IAG Symposium on Airborne Gravity Field Determination. Athens: University of Calgary ,1995: 39-45. |
| [15] | NEUMEYER J, SCHFER U, KREMER J, et al. Derivation of Gravity Anomalies from Airborne Gravimeter and IMU Recordings Validation with Regional Analytic Models Using Ground and Satellite Gravity Data[J]. Journal of Geodynamics, 2009, 47(4): 191-200. |
| [16] | SUN Zhongmiao, ZHAI Zhenhe, LI Yingchun. Analysis on the Resolution and Accuracy of Airborne Gravity Survey[J]. Progress in Geophysics, 2010, 25(3): 795-798. (孙中苗, 翟振和, 李迎春. 航空重力测量的分辨率和精度分析[J]. .地球物理学进展, 2010, 25(3): 795-798) |
| [17] | SUN Zhongmiao, SHI Pan, XIA Zheren, et al. Determination of the Vertical Acceleration for Airborne Gravimetry Using GPS and Digital Filtering[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(2): 110-115. (孙中苗, 石磐, 夏哲仁, 等. 利用GPS和数字滤波技术确定航空重力测量中的垂直加速度[J]. 测绘学报, 2004, 33(2): 110-115.) |
| [18] | XIA Zheren, SHI Pan, SUN Zhongmiao, et al. Chinese Airborne Gravimetry System CHAGS[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(3): 216-220. (夏哲仁, 石磐, 孙中苗, 等. 航空重力测量系统CHAGS[J]. 测绘学报, 2004, 33(3): 216-220.) |
| [19] | XIAO Yun , XIA Zheren. Determination of Moving Base Acceleration in Airborne Gravimetry[J]. Chinese Journal of Geophysics, 2003, 46(1): 62-67. (肖云, 夏哲仁. 航空重力测量中载体运动加速度的确定[J]. 地球物理学报, 2003, 46(1): 62-67.) |
| [20] | SUN Zhongmiao, XIA Zheren. Design of FIR Lowpass Differentiator and Its Applications in Airborne Gravimetry[J]. Chinese Journal of Geophysics, 2000, 43(6): 850-855. (孙中苗, 夏哲仁. FIR低通差分器的设计及其在航空重力测量中的应用[J]. 地球物理学报, 2000, 43(6): 850-855.) |
| [21] | LIU Lintao, XU Houze. Wavelets in Airborne Gravimetry[J]. Chinese Journal of Geophysics, 2004, 47(3): 490-494 (柳林涛, 许厚泽. 航空重力测量数据的小波滤波处理[J]. 地球物理学报, 2004, 47(3): 490-494.) |
| [22] | LIANG Xinghui, LIU Lintao, YU Shenjie. The Application of B Spline Least Squares in Determining Moving-base Acceleration for Airborne Vector Gravimetry[J]. Geomatics and Information Science of Wuhan University, 2009, 34(8): 979-982. (梁星辉, 柳林涛, 于胜杰. 利用B样条确定航空重力载体加速度的方法研究[J]. 武汉大学学报: 信息科学版, 2009, 34(8): 979-982.) |
| [23] | TORGE W. Gravimetry[M]. New York: Walter de Gruyter,1989. |
| [24] | ZHANG Shanyan, LI Xiqi. New Developed CHZ Sea-gravimetry[J]. Acta Geodaetica et Cartographica Sinica,1987, 16(1): 1-16. (张善言, 李锡其. 新研制的海洋重力仪[J]. 测绘学报, 1987, 16(1): 1-16.) |
| [25] | DONG Xia, CHEN Kangning, LI Tianshi. Mechanical Control Theory[M]. Xi’an: Xi’an Jiaotong University Press, 2005. (董霞, 陈康宁,李天石. 机械控制理论基础[M]. 西安: 西安交通大学出版社, 2005.) |