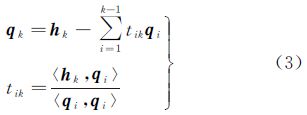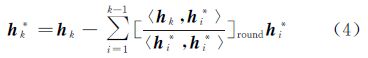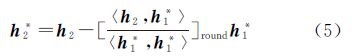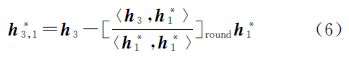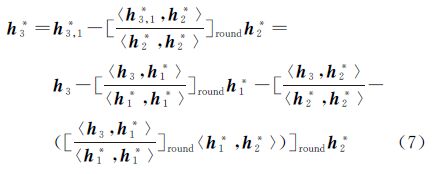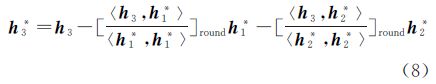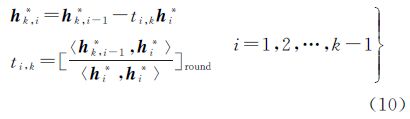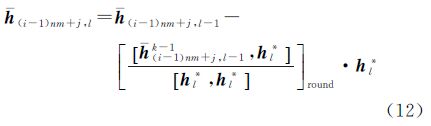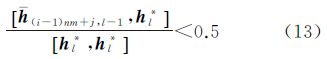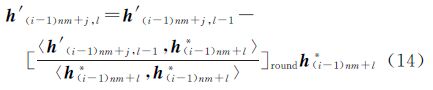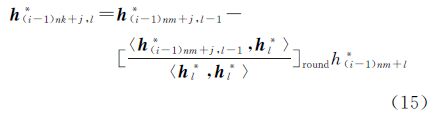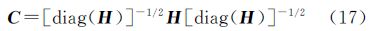2. 信息工程大学 地理空间信息学院,河南 郑州 450052
2. Institute of Geospatial Information,Information Engineering University,Zhengzhou 450052,China
1 引 言
基于模糊度域[1, 2]进行模糊度解算的方法中,由于实数解之间存在较强的相关性,导致构造出搜索空间的形状呈扁长的椭球体,这将会严重影响搜索的效率,并且最终可能导致解算失败。为了改善这种情况,在搜索之前有必要对实数解进行降相关处理。文献[3, 4, 5]提出最小二乘去相关算法(LAMBDA),通过构造整数高斯变换矩阵对实数解进行降相关处理;文献[6]对LAMBDA算法的整个过程进行了详细介绍,并提出系统配对的策略来构造Z变换矩阵; 文献[7, 8]提出基于Cholesky分解的模糊度降相关算法;文献[9]提出多次整数三角分解降相关的方法;文献[10]提出利用递归的方法直接最小化转换矩阵的对角线元素的方法;文献[11]提出对模糊度协方差矩阵的对角线元素进行排序的降相关算法;文献[12]基于格理论的相关应用,设计了著名的LLL规约算法,近年来该算法在格基规约领域得到了深入的研究和广泛的应用;文献[13]对LLL规约算法进行转化,将其应用到模糊度降相关中;文献[14]利用随机模拟的方法计算出模糊度协方差矩阵,对LLL降相关算法进行分析研究,并与整数高斯变换、整数Cholesky分解等算法进行比较;文献[15]针对LLL降相关算法在取整过程中会引入较大的舍入误差的问题,提出基于矩阵整体进行取整的改进的LLL算法。以上几种LLL算法均是基于经典的Gram-Schmidt正交化(CGS)。文献[16]提出基于修正的Gram-Schmidt正交化(MGS)变换[17]的LLL算法。随着GPS的现代化进程、GLONASS的补充更新计划、Galileo和我国北斗系统的逐步建设与应用,GNSS系统呈现出多模式、多频段的发展趋势,有更多的观测信息可供用户使用,进而模糊度实数解协方差矩阵的维数也会随之增大。LLL降相关算法基于低级的基本线性代数子程序(basic linear algebra subprograms,BLAS)运算[18]。算法对向量逐一循环进行整数正交变换,由于取整舍入误差的影响,经过变换后向量之间不能完全正交,在对下一个向量进行处理时,舍入误差也会随着之前经过变换的向量代入正交化的过程中,随着循环的进行,其舍入误差累积的影响越来越严重。高维情况下,可能会导致降相关失败。针对实数解协方差矩阵高维情况下降相关的问题,本文设计了整数分块正交化算法,并将其应用到降相关中,提出基于整数分块正交化的LLL降相关算法(IBGS-LLL)。利用随机模拟的数据,分析了不同维数情况下,不同分块方式对算法降相关效果的影响,利用IBGS-LLL算法在静态和动态情况下,分别选用不同的分块方式与改进的LLL算法[15]进行比较,结果表明IBGS-LLL算法的平均相关系数和条件数的改善程度均优于改进的LLL算法。经过IBGS-LLL算法降相关之后的协方差矩阵更加接近对角阵,进而较好地改善了模糊度的搜索空间。
2 整数分块Gram-Schmidt正交化算法分块Gram-Schmidt正交化算法(BGS)[18, 19, 20]首先将矩阵中所有的列向量分为若干块,而后对每个分块矩阵逐一进行正交化和重正交化变换,保证了高维情况下算法的效果和稳定性。基于模糊度降相关中对变换矩阵的要求,本文设计了整数分块Gram-Schmidt正交化算法(IBGS)。
BGS算法同CGS算法一样,都保证了矩阵中的每个列向量经过正交化变换。不同的是,CGS算法是对每个向量逐一进行变换的一层循环过程,而分块正交化算法是包括对每个矩阵块进行遍历处理和对矩阵块内部所包含的向量逐一进行处理的内外两层循环过程。
首先对每个向量的正交化过程进行分析,对于列满秩矩阵H=[h1 h2…hn],假设其前k-1个向量已经进行了正交变换后得到相互正交的向量q1,q2,…,qk-1,则第k个向量hk首先与q1进行正交化变换
式中,〈,〉为两个向量的内积运算。在得到qk,1的基础上与q2进行正交化变换
由于在之前变换中已保证〈q1,q2〉=0,因此上式可改写为 依次循环直到经过k-1次变换之后即可得到与前k-1个向量正交的qk,其整个变换过程可归纳为
依次循环直到经过k-1次变换之后即可得到与前k-1个向量正交的qk,其整个变换过程可归纳为
为了保证模糊度的整数特性,LLL算法[13, 14, 15]将式中的系数tik直接取整,即
式中,[]round为取整运算符;h1*=h1;h2的正交化向量可表示为
对于第3个向量h3来说,按照式(1)和式(2)中所示的标准正交化过程,首先与h1*进行正交化得
而后在前一步得到的h3,1*的基础上,与h2*进行正交化
由于取整舍入误差的影响,〈h1*,h2*〉≠0,所以 。LLL算法中的整数GS正交变换并未考虑到〈h1*,h2*〉≠0的情况,直接对式中的tik进行取整得到向量h3的正交化向量为
。LLL算法中的整数GS正交变换并未考虑到〈h1*,h2*〉≠0的情况,直接对式中的tik进行取整得到向量h3的正交化向量为
这相当于在取整引入舍入误差的基础上,又引入了新的误差ε3
该误差是由于经过整数GS变换后的向量之间不能完全正交而引起的。随着对其余向量逐一进行正交变换,该误差还会累积,越往后影响越大。依据标准GS正交变换的原理,对于每个向量,应采用如式所示的正交化过程。对于k=2,3,…,n
式中,hk,0*=hk。变换过程中通过利用前一次变换后的向量计算第i个向量对应的正交化变换系数,避免了由于两个向量不能完全正交而在系数计算时产生的误差,仅受到取整舍入误差的影响。
结合以上讨论的对于每个向量的整数正交化过程和分块正交算法[18]即可设计相应的IBGS算法。由于矩阵H=[h1 h2…hn]的n个列向量之间不存在相关性。将H按其列向量分为m个矩阵块,每块由nm个向量组成。
首先展开i=1,2,…,m的外层循环过程。与CGS算法不同的是,当i=1时分块算法对应的是一个矩阵块而不是向量,所以必须对矩阵块H1=[h1 h2…hnm]进行变换处理,以保证其内部向量之间的正交特性和后续正交化过程的顺利进行。利用式(10)所示向量的整数正交化过程进行变换,由于取整运算舍入误差的存在,hk经过一次整数正交化变换之后,其与前k-1个向量之间的正交程度还不满足要求,可以进行多次迭代,直到该向量对应的所有正交化系数的实数值都小于0.5时停止迭代。变换可由矩阵表示为
式中,H1*=[h1* h2*…hnm*]为分块矩阵中向量经过变换后的结果;R1=[Tnm-1][Tnm-1-1]…[T1-1],Ti为第i个向量的变换矩阵,其所有元素均为整数,且满足行列式为1条件。
在保证第1个分块矩阵完成整数正交变换之后,即可对其余m-1个分块矩阵进行遍历处理。本文将每个具体的分块矩阵进行正交化变换的过程分为外变换、内变换两个部分,其中外变换为当前第i个分块矩阵与之前i-1个分块之间的整数正交化变换;内变换包括当前分块内部各向量之间的变换和与之前向量的重正交变换。内层j=1,2,…,nm的循环过程就在这两个部分中分别展开。
(1) 外变换部分:对于第i≥2个分块矩阵Hi=[h(i-1)nm+1 h(i-1)nm+2…hi×nm],为了使其与之前经过整数正交变换的(i-1)×nm个列向量正交,Hi中的各向量需要首先与之进行正交变换,其具体变换过程为
式中,h(i-1)nm+j,0=h(i-1)nm+j;j=1,2,…,nm;l=1,2,…,(i-1)nm+j-1。同样的,为了保证正交化的效果,这个过程也需要迭代直到该向量对应的变换系数全部满足
停止迭代,分块矩阵中所有nm个向量经过变换后可得Hi=[h(i-1)nm+1 h(i-1)nm+2…hi×nm]及变换矩阵Rj。
(2) 内变换部分:此部分的变换是以实现分块矩阵内部各向量之间相互正交为目的。由于h(i-1)nm+1在内变换过程中作为第1个向量,为了保证后面向量能够正确的进行变换,需要依据式(12)所示的变换过程,与之前的(i-1)nm个变换后的向量进行一次整数重正交变换并最终得到h(i-1)nm+1*。对于Hi中的第j≥2个向量,在分块内部进行如下变换
式中,h′(i-1)nm+j,0=h(i-1)nm+1(i-1)nm+j,l=1,2,…,j-1,对这个过程进行多次迭代,当达到与式(13)相同的条件时停止,得到变换后的向量h′(i-1)nm+j。
经过以上过程之后,当前向量已经完成与其之前所有分块矩阵和当前分块中的向量的整数正交变换,为了进一步保证该向量与之前所有向量的正交化程度,再进行一次整数重正交变换
式中,h(i-1)nm+j,0*=h′(i-1)nm+j;l=1,2,…,(i-1)nm+j-1。同样的,这个过程也需要多次迭代,最终得到向量h(i-1)nk+j*。
经过内外层循环过程即可完成对矩阵H的整数正交变换
得到能够满足近似正交的矩阵H*及相应的转换矩阵R,是由若干个满足降相关条件的变换矩阵相乘得到的,因此也满足所有元素为整数且行列式为1的条件。
3 基于整数分块正交化的LLL降相关算法基于第2节提出的算法,本文设计了基于整数分块GS变换的降相关算法(IBGS-LLL),其具体过程如下:
(1) 利用Cholesky分解对模糊度实数解的协方差矩阵进行分解Qâ=HTH,得到上三角矩阵H。
(2) 考虑到降相关变换矩阵整数的特性,为了提高其变换性能,在变换之前需要对矩阵的列向量进行重新排列,使其相应的正交化向量的高斯范数能够尽可能地按照由小到大的顺序,参考文献[21, 22],利用系统旋转变换的方式构造初等变换矩阵U,并对上三角矩阵进行变换H=HU。
(3) 利用IBGS算法对重排列之后的矩阵进行整数正交变换,得到矩阵H*=HR。
经过以上3步变换之后,H*中的列向量之间能够满足近似的正交,但是由于整数变换的特点,其正交变换还不彻底,为了保证变换之后各向量之间的夹角能够尽可能接近90°,需要对整个过程进行迭代,即对H*再进行步骤(2)和步骤(3)的处理。本文引入平均相关系数来判断迭代是否终止。其具体定义为,首先对于一个矩阵H,可定义其相关矩阵为[23]
进而其平均相关系数可定义为所有相关系数的平均值
每一次整体变换之后都计算出一个γ值,通过试验分析,经过一定次数的迭代之后实数解协方差矩阵的平均相关系数不会再发生变化,因此可将判断标准设置为当γi=γi-1时迭代停止。从而步骤(3)可改变为利用IBGS算法对重排列之后的H矩阵进行整数正交变换,得到矩阵H*,计算其相应的平均相关系数,判断其是否等于上次计算的平均相关系数,若相等则停止迭代否则重复步骤(2)和步骤(3)。
经过k次迭代之后得到最终的整数转换矩阵Rall=U1R1…UkRk,由于初等变换矩阵Ui满足所有元素为整数且行列式为1的条件,因此Rall满足降相关变换矩阵的要求。相应的降相关之后的模糊度实数解 =Rall-1â和协方差矩阵为Qâ*=RallTQâ*Rall,利用其即可构建搜索区域对模糊度进行固定,得到整数解向量z,而后再利用整数变换矩阵将其转换最终的整周模糊度解a=Rall。
=Rall-1â和协方差矩阵为Qâ*=RallTQâ*Rall,利用其即可构建搜索区域对模糊度进行固定,得到整数解向量z,而后再利用整数变换矩阵将其转换最终的整周模糊度解a=Rall。
每一组GNSS观测数据都对应着一定的观测模式和特定的卫星与测站之间的几何结构关系,若只用一组数据进行计算分析,不能在普遍意义下说明算法的正确性和有效性。为此,本文采用随机模拟的方法[14],模拟出模糊度实数解的协方差矩阵进行计算分析。
IBGS-LLL算法基于分块正交变换对实数解的协方差矩阵进行处理,算法通常是先将矩阵按其列向量均匀的分成若干子块后,再对其进行变换。对于不同的观测数据,模糊度实数解协方差矩阵的维数并不相同,当矩阵的维数为因数时,可以将其均匀分块;当为素数时,最简单的方法就是将其分成两个子块,同时可以更加细致地将矩阵分为m个子块,其中每个子块包含两个列向量,本文将这两种分块方式分别简称为B-2和B-m2,在矩阵维数不确定的情况下,相比较而言这两种分块方式在形式上是比较均匀的。不同的分块方式,算法的计算结果和效率也不相同,有必要在不同的分块情况下对算法进行分析,从而确定最佳的分块方式以保证降相关的顺利进行。
首先在固定模糊度未知参数个数的情况下,模拟维数分别为n=9、n=25和n=50各200组协方差矩阵,对各维数进行具体分块为[m=5,m=3,m=2]、[m=13,m=5,m=2]和[m=25,m=10,m=2],利用IBGS-LLL算法下进行分析,模拟的固定维数下的3种情况,原始的协方差矩阵的条件数一般在104~108的范围内变化,矩阵维数越小,γ越大,模糊度实数解之间的相关性越强。对固定维数情况下的结果进行了统计,计算出相应的平均降相关系数的平均值γ、条件数的平均值c和算法耗时的平均值t,如表 1所示。
| γ | c | t/s | ||
| 9维 | orginal | 0.816 5 | 4.38e5 | - |
| m=5 | 0.164 1 | 0.64e2 | 0.012 9 | |
| m=3 | 0.163 4 | 0.62e2 | 0.013 1 | |
| m=2 | 0.163 1 | 0.51e2 | 0.013 2 | |
| 25维 | orginal | 0.544 0 | 7.20e5 | - |
| m=13 | 0.107 7 | 3.61e2 | 0.022 0 | |
| m=5 | 0.107 8 | 3.84e2 | 0.024 4 | |
| m=2 | 0.108 4 | 5.60e2 | 0.027 0 | |
| 50维 | orginal | 0.332 2 | 1.28e6 | - |
| m=25 | 0.062 7 | 1.31e3 | 0.122 4 | |
| m=10 | 0.063 0 | 3.35e3 | 0.123 5 | |
| m=2 | 0.062 6 | 0. 89e3 | 0.124 4 |
经过IBGS-LLL算法处理之后,对于不同的分块情况,其平均相关系数和条件数都有明显的改善,都能够成功地实现降相关。由于3种情况下的维数均为因数,都存在除了1和其本身之外可被整除的数,每种维数情况下都采用了B-2和B-m2的分块方式,无论在均匀分块的情况下(如50维),还是在不均匀分块的情况下(如9维、25维),两种分块方式与其他均匀的分块的计算结果一致。由表可知,这3种维数情况下,原始协方差矩阵的γ都大于0.3,c都大于105。
不同分块方式下,其结果较原来都有明显的改善。随着矩阵维数的增大,结果的条件数虽然有所改善,但是却越来越大;而平均相关系数的均值随着维数的增大越来越小,在50维的情况下均明显小于0.1。这是由于原始矩阵的相关程度随着维数的增加而降低,算法迭代的次数比低维的情况少,并且矩阵的条件数仅反映最大和最小特征之间的差距,并不能反映整个矩阵的相关性,从而导致表中所示的结果。在算法的运行时间方面,随着维数的增加算法的耗时也相应增大,不同分块方式的耗用时间基本相同,相差最大也仅为毫秒的量级。由此可知,固定维数的情况下,B-2和B-m2的分块方式无论能否实现均匀的分块,都可成功实现降相关,并且效果与其他均匀分块方式一致。为进一步进行分析,利用B-2和B-m2的分块方式在维数不固定的情况下,分别模拟了低维n∈[4, 20]和高维n∈[21, 100]两种情况下各200组数据进行降相关变换。对结果进行了统计,如表 2所示。
| γ | c | t/s | ||
| n∈[4, 20] | orginal | 0.844 4 | 4.43e5 | - |
| B-m2 | 0.152 2 | 1.02e2 | 0.006 3 | |
| B-2 | 0.152 3 | 1.48e2 | 0.006 8 | |
| n∈[21, 100] | orginal | 0.313 5 | 3.24e5 | - |
| B-m2 | 0.059 1 | 1.33e3 | 0.282 4 | |
| B-2 | 0.059 0 | 1.10e3 | 0.297 5 |
表 2反映了原始矩阵及B-m2和B-2两种分块方式结果的平均相关系数的均值span style="text-decoration:overline">γ、条件数的均值span style="text-decoration:overline">c。由这两个值可知,两种分块方式在维数随机的情况下,降相关的效果明显。低维情况下B-2方式的平均相关系数、条件数及算法的效率与B-m2相比都略差;高维情况下,两种方式的平均降相关系数是很一致的,同时由于B-2分块得到的子块维数比较大,需要经过更多次的迭代,所以耗时比B-m2稍长,但其量级也仅为0.01 s。在条件数的改进方面,B-2明显优于B-m2。这是由于高维情况下细致的分块方式,因分块数的增多,其累计误差对正交化的过程影响明显,而B-2的分块方式,虽然在每个子块内需要经过更多次迭代,但是其受到的累积误差明显小于B-m2,所以其综合效果要好一些。由以上分析可知,低维情况下可以选用B-m2的分块方式,高维情况下可选用B-2的分块方式。
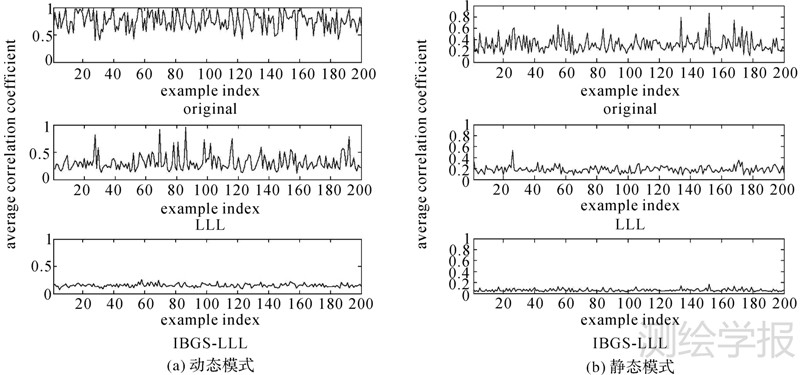
由于文献[14, 15]中提到的LLL降相关算法受到舍入误差的影响非常大,其效果和成功率都比较低,在实际降相关应用中很少被使用。文献[16]通过模拟计算证明了基于矩阵整体变换的改进的LLL降相关算法,对于协方差矩阵的条件数和平均相关系数的改进都明显优于LLL降相关算法,为了说明IBGS-LLL算法的降相关效果,本文采用基于改进的LLL降相关算法[15]代替LLL算法(在后面的图表中以LLL作为其相应的标识)分别在动态和静态两种模式下与IBGS-LLL算法进行分析比较。动态模式下,由于载体状态变化大、观测时间短,从而可观测到的卫星数目少,模糊度未知参数的个数一般在4~10之间变化;静态模式下,由于接收机状态稳定,观测时间长,单系统双频情况下模糊度未知参数在11~50之间变换[14],GNSS多系统下,用户可接收到不同系统多个频段的观测信号,为了充分验证IBGS-LLL算法在GNSS多系统下的有效性和正确性,本文设动态情况下模糊未知个数在4~20之间变化,静态情况下在21~100的范围变化。本文在静态选用基于B-2的分块方式、动态选用基于B-m2的分块方式的IBGS-LLL算法。模拟了两种状态下各200组数据进行计算,结果如图 1、图 2所示。
|
| 图 1 动态和静态模式下的平均降相关系数 Fig. 1 The average correlation coefficient under the kinematic and static mode |

|
| 图 2 动态和静态模式下的条件数 Fig. 2 The condition number under the kinematic and static mode |
图 1、图 2显示了动态和静态两种情况下,200组数据的原始矩阵、改进的LLL降相关算法和IBGS-LLL算法结果的平均相关系数和条件数,其中左侧为动态的情况,右侧为静态的情况。两种方法基本都能完成降相关,IBGS-LLL算法的结果明显优于改进的LLL算法。对结果的平均相关系数和条件数与原始矩阵进行比较,当两个指标均小于随机模拟的原始矩阵,则降相关成功,否则降相关失败。对所有的200组结果进行分析即可计算出降相关的成功率。在动态情况下,由于矩阵维数较低,两种算法都可保证百分之百降相关成功;而静态情况下,随着维数的增加,改进的LLL算法的结果出现了条件数和平均相关系数大于原始矩阵的情况,经过变换后协方差矩阵中元素的量级明显增大,说明降相关失败,静态高维情况下其降相关的成功率为92.5%;而IBGS-LLL算法的两种指标都有明显的改善,其成功率则依然可保证100%。
为了进一步突出本文所提算法在高维情况下的优势,选取了静态情况下的10组数据,详细分析了其相应的平均相关系数和条件数的变化以及算法耗时,见表 3。
| unknown number | original | LLL | IBGS-LLL | |||||||
| condition number | average correlation coefficient | condition number | average correlation coefficient | time/s | condition number | average correlation coefficient | time/s | |||
| 22 | 2.45e4 | 0.338 4 | 1.73e2 | 0.125 8 | 0.016 | 0.96e2 | 0.094 9 | 0.016 | ||
| 39 | 4.10e4 | 0.337 0 | 5.22e2 | 0.129 7 | 0.047 | 2.09e2 | 0.070 2 | 0.062 | ||
| 45 | 8.95e5 | 0.333 0 | 1.09e3 | 0.154 4 | 0.078 | 3.76e2 | 0.066 6 | 0.110 | ||
| 50 | 3.73e5 | 0.427 1 | 3.77e3 | 0.246 9 | 0.093 | 3.13e3 | 0.069 4 | 0.125 | ||
| 64 | 1.73e5 | 0.317 9 | 5.35e4 | 0.306 41 | 0.125 | 6.91e2 | 0.055 5 | 0.296 | ||
| 75 | 6.48e4 | 0.237 9 | 4.42e3 | 0.148 1 | 0.328 | 1.14e3 | 0.043 6 | 0.450 | ||
| 83 | 3.67e5 | 0.215 8 | 3.71e5 | 0.216 2 | 0.234 | 2.15e3 | 0.036 7 | 0.485 | ||
| 88 | 6.02e5 | 0.254 5 | 6.01e5 | 0.263 0 | 0.360 | 1.00e3 | 0.044 5 | 0.657 | ||
| 90 | 1.96e5 | 0.184 8 | 2.04e5 | 0.190 2 | 0.313 | 1.69e3 | 0.031 28 | 0.547 | ||
| 92 | 5.36e4 | 0.190 9 | 5.29e4 | 0.195 5 | 0.359 | 7.26e2 | 0.031 6 | 0.610 | ||
由表 3可以看出静态情况下,随着矩阵维数的不断增加,改进的LLL算法的降相关能力逐渐降低,当高于一定的维数时就出现了降相关失败的情况,而本文提出的IBGS-LLL算法始终保持良好的降相关性能。同时注意到随着维数的增加,两种算法的耗时也随之而增加,由于本文提出的IBGS-LLL算法涉及内外变换以及重正交的过程,所以其耗时略高于改进的LLL算法,但是两种方法的差别在0.5 s以内。
为了进一步分析说明算法在模糊度解算中的作用,选取2012-04-26美国连续运行参考站(http://www.ngs.noaa.gov/CORS)的GPS单系统双频的观测数据进行计算。
方案1:选取了scgp和scgt两个测站24 h的数据,其采样间隔为30 s,共包含78个模糊度未知参数。
方案2:选取了waar和midt两个测站10个历元的数据,其采样间隔为1 s,模糊度未知参数的个数为7。
这两种方案分别是为了验证高维情况下和快速定位情况下,算法的效果。在计算出其模糊度实数解及协方差矩阵之后,分别在未进行降相关、改进的LLL降相关和本文提出的IBGS-LLL降相关的情况下,进行模糊度搜索固定,统计了3种情况下,矩阵的条件数和平均相关系数。由于降相关的目的是为了提高搜索的效率和成功率,为了体现算法在这方面的效果,本文还对经过降相关之后的模糊度搜索的时间和结果进行了分析,计算了不同情况下Bootstrapping算法的成功率[24]
式中, 。结果如表 4所示。
。结果如表 4所示。
| original | LLL | IBGS-LLL | ||
| 方案1 | condition number | 1.26e5 | 1.32e3 | 0.58e2 |
| average correlation coefficient | 0.16 | 0.07 | 0.02 | |
| bootstrapping success rate | 7.68e-39 | 2.63e-38 | 3.29e-38 | |
| time/s | 184.66 | 130.25 | 0.03 | |
| 方案2 | condition number | 1.14e10 | 4.97e4 | 4.39e4 |
| average correlation coefficient | 0.31 | 0.13 | 0.12 | |
| bootstrapping success rate | 0.22 | 0.67 | 0.78 | |
| time/s | 6.21 | 0.34 | 0.01 |
如表 4所示,对于实测数据来说,其协方差矩阵的条件数和平均相关系数与本文模拟的情况大体上是一致的,在低维情况的条件数和平均相关系数都大于高维的情况,两种方案经过IBGS-LLL和改进的LLL降相关处理之后,条件数和平均相关系数两种指标都有所改进,并且IBGS-LLL算法的优化程度优于改进的LLL算法。方案1高维情况下,原始协方差矩阵的Bootstrapping算法的成功率非常低;方案2低维情况下,由于模糊度参数的维数较低,所以原始协方差矩阵的成功率比高维的要高。经过降相关变换之后其成功率都得到了改善,并且本文提出的IBGS-LLL算法的成功率均优于改进的LLL降相关算法。搜索时间方面,方案1基于原始的协方差矩阵的模糊度搜索时间需要3 min多,方案2快速定位情况下也需要6 s,说明原始矩阵的搜索效率较低;而经过改进的LLL降相关之后,虽然两种评价指标得到了改善,但是高维情况下,其计算效率的改善效果并不太明显,在快速定位情况下,由于模糊度维数较低改进的LLL算法受到舍入误差影响不明显,因此还是能够在1之内获得模糊度的解;基于IBGS-LLL降相关的方式,明显提高了搜索的效率,无论针对方案1还是方案2的数据,都能够以很快的速度获得模糊度解,这更加验证了本文算法的有效性,说明IBGS-LLL算法能够较好地优化模糊度的搜索空间,提高搜索效率。为了进一步说明本文算法对于提高模糊度解算效率的作用,列举了方案2中原始的模糊度的浮点解、固定解和经过IBGS-LLL降相关的浮点解及其相应的固定解,如表 5所示。
| â | a |  | z | aIBGS-LLL |
| 0 | 0 | 0 | 0 | 0 |
| -1 517 785.4 | -1 517 629 | 10 672 410.6 | 10 672 411 | -1 517 629 |
| -2 459 601.1 | -2 459 552 | 13 239 829.9 | 13 239 830 | -2 459 552 |
| -2 459 621.8 | -2 459 478 | 6 334 850.9 | 6 334 851 | -2 459 478 |
| -2 459 631.7 | -2 459 451 | -95 192 508.2 | -95 192 508 | -2 459 451 |
| -2 459 604.7 | -2 459 530 | 20 414 401.1 | 20 414 401 | -2 459 530 |
| -2 459 614.1 | -2 459 550 | -39 827 420.9 | -39 827 421 | -2 459 550 |
表 5中,â和a分别表示原始的实数解和固定解; 和z分别表示经过降相关变换之后的实数解和固定解;aIBGS-LLL=Rallz。如表 5所示,未进行处理之前浮点解和固定解之间存在很大的差异,基本都在40以上,此时对浮点解进行搜索固定的过程肯定需要多次的迭代计算;而经过本文提出的IBGS-LLL降相关之后,模糊度的浮点解发生了改变,同时搜索得到的固定解与浮点解之间的差异很小,均小于0.5,通过对浮点解进行直接取整也可获得固定解,这说明经过变换之后,浮点解之间的相关性得到了很大程度的减弱,基于浮点解和协方差矩阵只需要耗费较少的搜索计算步骤即可获得正确的结果。
和z分别表示经过降相关变换之后的实数解和固定解;aIBGS-LLL=Rallz。如表 5所示,未进行处理之前浮点解和固定解之间存在很大的差异,基本都在40以上,此时对浮点解进行搜索固定的过程肯定需要多次的迭代计算;而经过本文提出的IBGS-LLL降相关之后,模糊度的浮点解发生了改变,同时搜索得到的固定解与浮点解之间的差异很小,均小于0.5,通过对浮点解进行直接取整也可获得固定解,这说明经过变换之后,浮点解之间的相关性得到了很大程度的减弱,基于浮点解和协方差矩阵只需要耗费较少的搜索计算步骤即可获得正确的结果。
本文将分块正交的思想引入模糊度降相关中,设计了整数分块正交化算法,与LLL降相关算法相结合,提出了基于整数分块正交化的LLL降相关算法(IBGS-LLL),通过比较分析得出了如下结论:
(1) LLL算法中整数正交变换的向量正交化过程,在取整舍入误差的基础上还会受到向量之间不能完全正交而引起误差的影响,该误差随着正交化的进行会逐渐累积,最终影响降相关的效果。在对该误差分析的基础上,依据标准的向量正交化过程,对向量的整数正交化算法进行了明确,而后结合分块正交算法,设计了IBGS算法。该算法不但避免了由于向量不完全正交而在正交化过程中引起的误差,同时通过分块处理减弱了舍入误差的影响。
(2) 通过在几种固定维数下,对不同分块情况的计算分析发现,无论能否均匀分块,B-2和B-m2的分块方式都能够实现与其他均匀分块方式相当的降相关效果。在维数随机的情况下,B-m2在动态(低维)模式下的降相关效果略优于B-2的分块方式,而静态(高维)模式下,B-2的综合效果略优。
(3) 利用IBGS-LLL降相关在动态和静态模式下,分别选用B-m2和B-2的分块方式与改进的LLL降相关算法进行分析比较,结果表明改进的LLL算法在静态矩阵维数较高的情况下,出现了降相关失败的情况,而经过IBGS-LLL算法变换之后矩阵的平均相关系数、条件数均优于改进的LLL降相关算法,在高维情况下可百分之百实现降相关。同时基于一组实测数据分析了3种情况下搜索的效率,结果表明IBGS-LLL算法的效果非常明显,可有效地改善搜索空间,提高搜索效率。
致谢:感谢美国国家海洋和大气管理局(NOAA)下属的国家大地测量机构(NGS)提供的CORS数据。
| [1] | HATCH R, EULER H J. Comparison of Several AROF Kinematic Techniques[C]//Proceedings of IEEE Symposium on Position, Location and Navigation. Salt Lake City:IEEE, 1994: 363-369. |
| [2] | FREI E, BEUTLER G. Rapid Static Positioning Based on the Fast Ambiguity Resolution Approach “FARA”: Theory and First Results[J]. Manuscripta Geotaetica, 1990, 15(4): 325-356. |
| [3] | TEUNISSEN P J G. The Least-squares Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy, 1995, 70(1-2): 65-82. |
| [4] | TEUNISSEN P J G. The Success Rate and Precision of GPS Ambiguity[J]. Journal of Geodesy, 2000, 74(3-4): 321-326. |
| [5] | TEUNISSEN P J G, JONGE P D, TIBERIUS C C. The Least-squares Ambiguity Decorrelation Adjustment: Its Performance on Short GPS Baselines and Short Observation Spans[J]. Journal of Geodesy, 1997, 71(10): 589-602. |
| [6] | JONGE P D, TIBERIUS C. The LAMBDA Method for Integer Ambiguity Estimation: Implementation Aspects: LGR Series 12 [R]. Delft: Delft University of Technology, 1996. |
| [7] | TEUNISSEN P J G. A New Method for Fast Carrier Phase Ambiguity Estimation[C]//Proceedings of IEEE PLANS’94. Las Vegas: IEEE, 1994: 562-573. |
| [8] | ZHOU Yangmei, LIU Jingnan, LIU Jiyu. Return-calculating LAMBDA Approach and Its Search Space[J]. Acta Geodaetica et Cartographica Sinca, 2005, 34(4): 300-304. (周扬眉, 刘经南, 刘基余. 回代解算的LAMBDA 方法及其搜索空间[J]. 测绘学报, 2005, 34(4): 300-304.) |
| [9] | RIZOS C, HAN S. A New Method for Constraining Multi-satellite Ambiguity Combinations for Improved Ambiguity Resolution[C]//Proceedings of ION: GPS-95. Palm Springs: ION, 1995: 1145-1153. |
| [10] | LI Z, GAO Y. A Method for Construction of High Dimension Transformation Matrices in LAMBDA[J]. Geomatica, 1998, 52: 433-439. |
| [11] | LIU L T, HSU H T, ZHU Y Z, et al. A New Approach to GPS Ambiguity Decorrelation[J]. Journal of Geodesy, 1999, 73(9): 478-490. |
| [12] | LENSTRA A K, LENSTRA H W, LOVASZ L. Factoring Polynomials with Rational Coefficients[J]. Mathematische Annalen , 1982, 261(4): 515-524. |
| [13] | GRAFAREND E. Mixed Integer-real Adjustment(IRA) Problems: GPS Initial Cycle Ambiguity Resolution by Means of the LLL Algorithm[J]. GPS Solution, 2000, 4(2): 31-44. |
| [14] | XU P. Random Simulation and GPS Decorrelation[J]. Journal of Geodesy, 2001, 75(7-8): 408-423. |
| [15] | LIU Zhiping, HE Xiufeng. An Improved LLL Algorithm for GPS Ambiguity Resolution[J]. Acta Geodaetica et Cartographica Sinca, 2007, 36(3): 286-289. (刘志平, 何秀凤. 改进的GPS模糊度降相关LLL算法[J]. 测绘学报, 2007, 36(3): 286-289.) |
| [16] | YANG Ronghua, HUA Xianghong, LI Zhao, et al. An Improves LLL Algorithm for GPS Ambiguity Solution[J]. Geomatics and Information Science of Wuhan University, 2010, 35(1): 21-24. (杨荣华, 花向红,李昭, 等. GPS模糊度降相关LLL算法的一种改进[J]. 武汉大学学报: 信息科学版, 2010, 35(1): 21-24.) |
| [17] | ZHANG Xianda. Matrix Analysis and Applications[M]. Beijing: Tsinghua University Press, 2004.(张贤达. 矩阵分析与应用[M]. 北京: 清华大学出版社, 2004.) |
| [18] | ZHAO Tao, JIANG Jinrong. A Block Gram-Schmidt Algorithm with Its Application[J]. Journal of the Graduate School of the Academy of Sciences, 2009, 26(2): 224-228. (赵韬, 姜金荣. 分块Gram-Schmidt正交化算法及其应用[J]. 中国科学院研究生院学报,2009, 26(2): 224-228.) |
| [19] | JALHY W, PHILIPPE B. Stability Analysis and Improvement of the Block Gram-Schmidt Algorithm[J]. SIAM Journal on Scientific and Statistical Computing, 1991, 12(5): 1058-1073. |
| [20] | STATHOPOULOS A, WU K. A Block Orthogonalization Procedure with Constant Sysnchronization Requirements[J]. S SIAM Journal on Scientific and Statistical Computing, 2002, 23(6): 2165-2182. |
| [21] | LIU Jingnan, YU Xingwang, ZHANG Xiaohong. GNSS Ambiguity Resolution Using the Lattice Theory[J]. Acta Geodaetica et Cartographica Sinca, 2012, 41(5): 636-645. (刘经南, 于兴旺, 张小红. 基于格论的 GNSS 模糊度解算[J]. 测绘学报, 2012, 41(5): 636-645.) |
| [22] | XU P. Parallel Cholesky-based Reduction for the Weighted Integer Least Squares Problem[J]. Journal of Geodesy, 2012, 86(1): 35-52. |
| [23] | LIU Zhiping, HE Xiufeng, GUO Guangli, et al. Decorrelation Algorithms and Its Evaluation Indexes for GNSS Ambiguity Solution[J]. Geomatics and Information Science of Wuhan University, 2011, 36(3): 257-261. (刘志平, 何秀凤, 郭广礼, 等. GNSS降相关算法及其评价性指标研究[J]. 武汉大学学报: 信息科学版, 2011: 36(3): 257-261.) |
| [24] | TEUNISSEN P J G. Success Probability of Integer GPS Ambiguity Rounding and Bootstrapping[J]. Journal of Geodesy, 1998, 72(10): 606-612. |