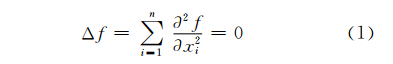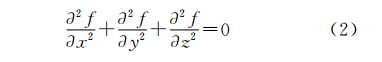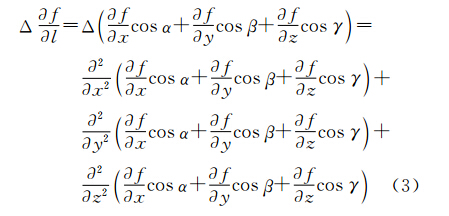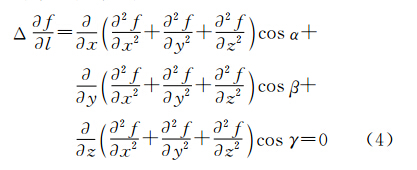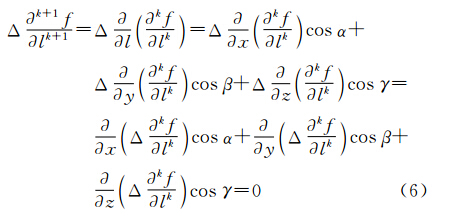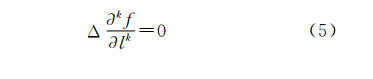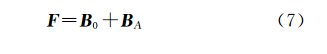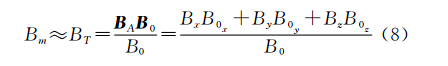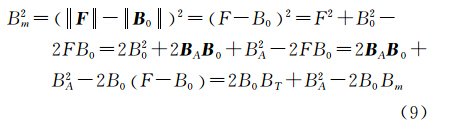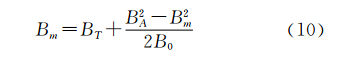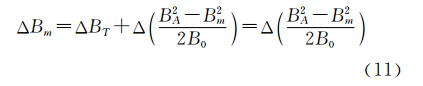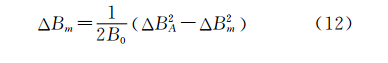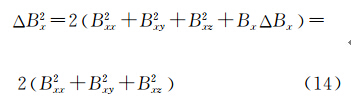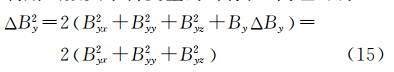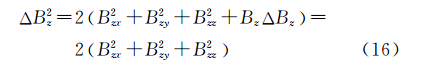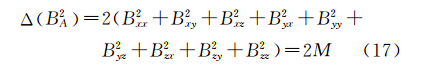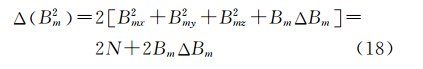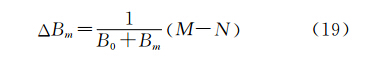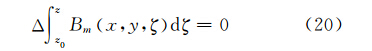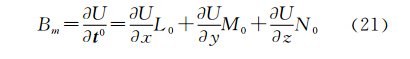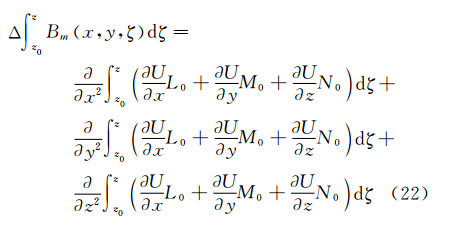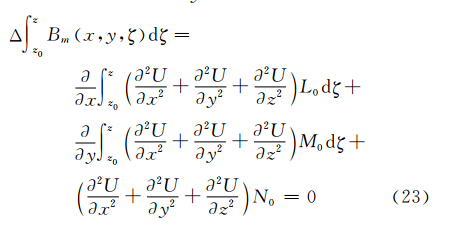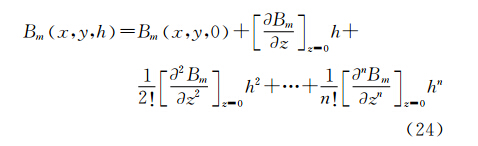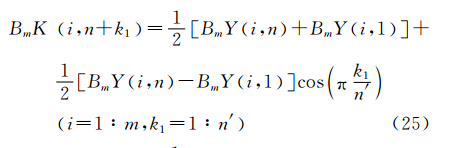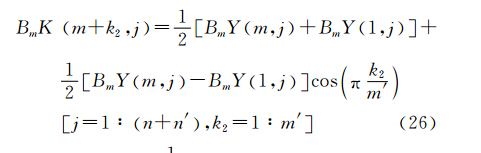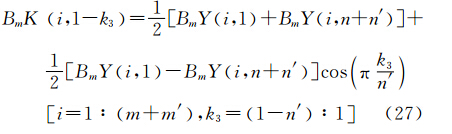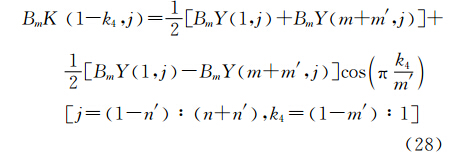2. 国家海洋局 海底科学重点实验室,浙江 杭州 310012;
3. 海军大连舰艇学院 海洋测绘科学与工程系,辽宁 大连 116018;
4. 海军海洋测绘研究所,天津 300061
2. Key lab of Submarine Geosciences, SOA, Hangzhou 310012, China;
3. Department of Hydrography and Cartography, Dalian Naval Academy, Dalian 116018, China;
4. Naval Institute of Hydrographic Surveying and Charting, Tianjin 300061, China
Corresponding author:ZHAI Guojun E-mail:zhaigj@163.com
1 引 言
磁场向下延拓是根据观测曲面或平面上位场数据,通过一定的数据处理手段获取靠近场源体附近磁场信息的过程[1]。通过向下延拓可以增强数据分辨率,反映局部磁场的细节信息,提高数据解释推断的可靠性[2]。由数学物理学可知,向下延拓属于典型的不适定问题[3]。围绕提高向下延拓的稳定性问题,国内外学者提出了诸多向下延拓方法,早期最为常用的向下延拓方法是FFT法,此外,还有正则化方法、Weiner滤波法、多尺度边缘约束法等[4, 5, 6]。然而,这些方法在实际应用中仍存在一定的局限性,如FFT法对噪声放大作用非常明显,会产生明显的Gibbs效应,一般只能向下延拓2~3倍数据点距;而正则化法属于有偏估计,如果正则化参数选择不当,可能引起较大的系统性偏差[7]。近年来,出现了一些关于向下延拓的最新研究成果,其中,文献[8]提出的积分-迭代法具有较好的计算效果和较大的向下延拓深度,文献[9]从数学角度证明了积分-迭代法能收敛到直接下延法理论解,该方法代表了国内向下延拓方面的较高水平,其适用性在航空磁测数据向下延拓中得到了验证。
上述讨论的向下延拓方法大多是利用磁场在无源空间内为调和场这一物理特性,将空间域的褶积关系转换成频率域的乘积关系进行解算。文献[10]从数学角度出发,分析多元泰勒级数法在位场延拓中应用的可行性,该方法应用的关键和难点在于怎样精确获取磁场各阶垂向导数[11]。文献[12]提出联立向上延拓和向下延拓公式来消除表达式中的奇次项,文献[13]根据磁场及其垂向导数在频率域的频谱关系,应用FFT法求解磁场各阶垂向导数。这些方法在理论研究上取得了一定的效果,但一直未能在具体实践中得到普遍应用,主要原因是解算垂向导数的频率响应函数相当于高频放大器,且导数阶数越高,放大作用越显著。针对这些问题,笔者根据总强度磁异常为调和场这一特性,综合利用空域和频域计算,提出一种精确求解磁场各阶垂向导数的新方法,把这些导数代入泰勒级数公式即可实现磁场稳健向下延拓。同时,还给出了基于半余弦函数的扩边处理方案,以降低向下延拓过程中产生的边界效应。文中详细研究了该方法的基本原理和技术措施,通过实测数据检验了方法的有效性,并将其计算结果精度与其他延拓方法进行了对比分析。限于篇幅,文中没有详述其他几种常用方法的算法原理。
2 方法原理
2.1 关于调和函数的一个定理
设函数 f 在定义域 Ω 中任意点都存在连续的一阶、二阶导数,满足拉普拉斯方程式(1),则称函数 f 在域 Ω 中调和
在三维空间直角坐标系中,拉普拉斯方程可写成如下形式
定理:调和函数f 沿l方向的任意阶方向导数也是调和函数。
证明:用数学归纳法进行证明,以m表示方向导数的阶数。
(1) 当m=1时
式中,α、β和γ为方向l的方向角。
由于调和函数对x、y和z无穷阶可微,即其任意阶偏导数在域Ω中都连续,因此,偏导数的求解与求导次序无关,得
故,f 沿l方向的1阶方向导数是调和函数。
(2) 假定当m=k时,f 沿l方向的m阶方向导数是调和函数,即有
成立。
(3) 当m=k+1时
因此,调和函数f 沿l方向的任意阶方向导数仍是调和函数。
2.2 Bm 的准调和性及其性质
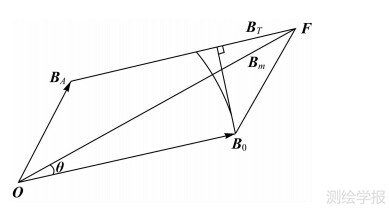
如图 1所示,实际观测的磁场总强度矢量F为地磁背景场矢量B0与磁异常强度矢量BA之和[14],即
|
| 图 1 各物理量关系图 Fig. 1 Relationship between physical symbols |
传统认为,当BAB0(为简化符号表述,以下用F、B0、BA和Bm分别表示F、B0、BA与Bm)时,可将总强度磁异常Bm近似看做是BA在B0方向的投影BT,即
式中,Bv和B0v(v=x、y、z)分别是磁异常强度与地磁场强度沿v方向的分量。
而实际观测得到的总强度磁异常Bm是F与B0的模量差
经整理后,得
对式(10)进行拉普拉斯算子( Δ=Δ 2)运算,并顾及 Δ BT≡0。得
在小尺度磁性目标探测中,可视地磁背景场B0为常数[15],故
由于
式中,Bxx= Bx x。而 Δ Bx≡0,因此
式中,Bxv= Bx v(v=x、y、z)。
利用函数关于自变量的对称性,同理可得
因而
式中,M=B2xx+B2xy+B2xz+B2yx+B2yy+B2yz+B2zx+B2zy+B2zz为全张量梯度模的平方。
同理,还可证明
式中,N=B2mx+B2my+B2mz为解析信号模(也称为总强度磁异常总梯度模)的平方。
将式(17)和式(18)代入式(12),得
文献[16]中对M和N物理性质和空间变化规律进行了详细分析。研究表明:M和N在空间变化规律及数值大小都差异较小,一般情况下,M和N的差值仅为几十 nT/m ,而在我国范围内B0介于35 000 ~50 000 nT 之间,两者比值非常小,因而 Δ Bm在数值上接近于零。笔者采用数值模拟试验对总强度磁异常的这一性质多次进行了验证,得到了相同的结论,即总强度磁异常近似满足拉普拉斯方程,本文称其为准调和函数。下文在求解总强度磁异常一阶垂向导数时,还需要用到如下性质:总强度磁异常沿垂直方向的积分是调和函数,即
下面对这个性质予以证明。
证明:如前所述,Bm可看成是BA沿地磁场方向t0的分量,即
式中,U为磁性目标引起的磁位;L0= cos I0 cos A0;M0= cos I0 sin A0;N0= sin I0;I0和A0分别为地磁场方向倾角和偏角。
将式(21)代入式(20)左端得
利用含参变量积分定理,将上式右端整理后,并顾及 Δ U= 2U x2+ 2U y2+ 2U z2=0,得
证明完毕。
2.3 改进泰勒级数向下延拓步骤
泰勒级数向下延拓公式为
式中,Bmx,y,0和Bmx,y,h分别为观测平面与延拓平面上测点(x,y)处总强度磁异常值;h为向下延拓深度。
在式(24)中,观测面上Bmx,y,0和向下延拓深度h是已知值,若要精确计算向下延拓值,关键是准确获取总强度磁异常沿垂直方向的各阶导数。目前,常规泰勒级数法的做法是利用总强度磁异常和其导数在频率域关系式,求解总强度磁异常沿垂直方向的各阶导数。如求解Bm的第i阶垂向导数时,首先把平面上总强度磁异常格网数据进行傅里叶变换,再将变换后频谱乘以垂向导数因子2 π u2+v21/2i,结合反傅里叶变换得到。这种垂向导数频率域响应相当于高频放大器,且导数的阶次越高,放大作用越明显。文献[17]提出采用加入圆滑因子来压制高频干扰的方法,对于较低阶次垂向导数计算结果取得了一定效果,但较高阶次计算结果仍然趋于发散。为了防止利用常规泰勒级数法向下延拓时出现发散现象,泰勒级数的截断阶数一般不宜过高,且深度越大,阶数应越低,通常只取至2阶左右。
根据上文推导的调和函数Bm物理性质,提出计算总强度磁异常沿垂直方向各阶导数新方法,其具体步骤为:
(1) 把观测平面上总强度磁异常格网数据进行傅里叶变换得到频谱FBmu,v,0,将该频谱乘以垂向积分因子12 π u2+v21/2,再利用反傅里叶变换即可得到总强度磁异常沿垂直方向的积分值Jx,y,0。
(2) 采用双三次样条曲线插值函数计算J(x,y,0)沿x方向和y方向的二阶导数,Jxx(x,y,0)与Jyyx,y,0。前面已证明,总强度磁异常沿垂直方向的积分是调和函数,则Bm一阶垂向导数为 Bm zz=0=Jzzx,y,0=-[Jxxx,y,0+Jyyx,y,0]
(3) 采用双三次样条曲线插值函数计算Bm在水平方向的两个二阶导数 2Bm x2与 2Bm y2,根据拉普拉斯方程得 2Bm z2z=0=- 2Bm x2z=0+ 2Bm y2z=0
(4) 由于调和函数沿l方向的任意阶导数都是调和函数,取l方向与z方向相同,根据拉普拉斯方程,得第j(j=3,4,…,n)阶垂向导数为 jBm zjz=0=- jBm xjz=0+ jBm yjz=0,其中 jBm xjz=0和 jBm yjz=0是采用双三次样条曲线插值函数计算 j-2Bm zj-2z=0沿x和y方向得到的二阶导数。
将总强度磁异常观测值和上述步骤得到的沿垂直方向各阶导数代入泰勒级数公式,即可实现总强度磁异常的向下延拓。需要说明的是,由于垂向积分因子12 π u2+v21/2相当于低通滤波器,起到了压制高频的作用,可以对高频噪声进行滤波。但是,在利用双三次样条函数求解水平方向二阶导数时,对边界处的二阶导数进行了强制置零处理,因而计算结果会存在不同程度的边界效应,且阶数越高,边界效应越明显。
2.4 半余弦函数扩边处理方案
几乎所有向下延拓方法都会产生边界效应,而已有的扩边方法通常会导致在数据接边处产生不光滑,从而导致高阶导数对高频干扰的放大作用更明显,应用效果欠佳。受数字信号处理一维扩边处理方法启发,将其引入并扩展至二维平面数据扩边处理中。用BmY1:m,1:n表示格网化后总强度磁异常数据矩阵,m和n分别为数据矩阵行数和列数。设需将磁场数据在平面四个方向上进行扩边,为简便计,令数据矩阵在行的上下两端扩边数目各为m′;在列的左右两侧扩边数目均为n′。扩边后数据矩阵可表示为BmK1-m′:m+m′,1-n′:n+n′,其中,BmK(i,j)=BmYi,j,(1≤i≤m,1≤j≤n)。采用的半余弦扩边处理方案为
上述半余弦函数扩边方案在接边处是光滑的,且扩边后测点数目无需为2的整数次幂 。
3 实测数据分析
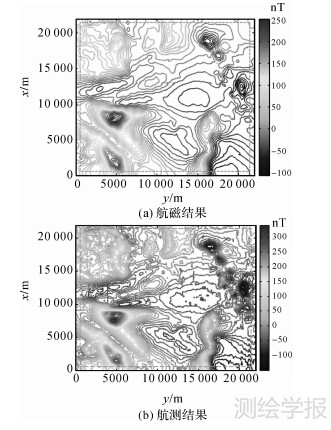
为检验本文方法在实践中的应用情况,采用文献[18—19]中实测资料进行分析。磁测资料是我国某海区船载磁力测量和航空磁力测量数据,选取其中部分重叠测区,面积为21 950×21 950 m2。船载磁力测量时布设的测线间距约100 m,测点间距约6 m;航空磁力测量时测线间距约250 m,测点间距约33 m,平均飞行高度是195 m。为更好地验证向下延拓结果的精度,采用连续曲率张力样条法对船载和航空磁测数据进行格网化,格网化后格网间距均为50 m×50 m。按照《海洋调查规范·海洋地质地球物理调查》[20]中给出的海洋磁测数据处理方法,对原始数据进行了粗差剔除、地磁日变改正、地磁日变基值归算、长期变化改正、船磁校正和正常场校正等数据处理后,航测和船测磁异常等值线如图 2所示,等值线间隔为10 nT。
|
| 图 2 测区航空和船载磁力测量总强度磁异常等值线图 Fig. 2 Contour map of total field magnetic anomaly from an airborne and seaborne magnetic survey |
从图 2(a)可以看出,航空磁力测量得到的总强度磁异常变化相对平缓,最大值为258.32 nT,最小值为-116.71 nT;船载磁力测量较航空磁力测量的观测面更接近于磁性体,能够反映磁场的细节信息,因而得到的总强度磁异常变化也较为剧烈,其最大值为339.15 nT,最小值为-148.21 nT。为了定量比较不同方法向下延拓精度,并排除边界效应对统计结果的影响,同时考虑到向下延拓深度较小(约4倍点距),选取图 2(a)中虚线框内格网点数据,即 D={(x,y )|550 m≤ x ≤21 400 m,550 m≤ x ≤21 400 m},采用的精度评价指标见式(29)
ρ=∑Nxi=1∑Nyj=1mi,j-Bmi,j2Nx×Ny (29)
假定船载磁力测量结果为真值,如果将航空磁力测量值不经过向下延拓,直接作为延拓结果与船载磁力测量值差值中误差为11.03 nT 。积分-迭代法是目前精度很高的向下延拓方法,因此,本文主要比较分析积分-迭代法和本文方法在实测数据处理中的应用效果。
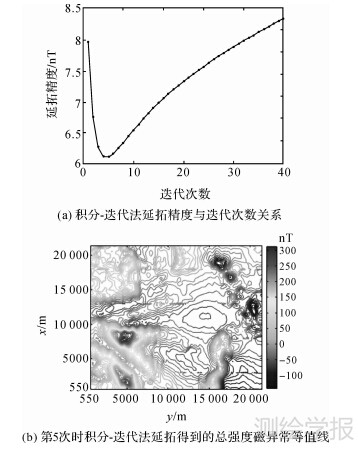
图 3是用积分-迭代法将 z =195 m高度的航空磁力测量总强度磁异常向下延拓至 z =0 m高度的结果,下延的深度约为4倍点距。图 3(a)中给出的是不同迭代次数时(本文取1~40次)积分-迭代法延拓至0 m高度后与船载磁力测量值差值的中误差,选取的迭代步长为0.5。可以看出,由于航空磁力测量成果数据中包含一定的误差,造成积分-迭代法延拓值与船载磁力测量值差值中误差随迭代次数的增加呈现先减小后增大的趋势,且在迭代次数为5次时中误差达到最小,精度最高。图 3(b)是积分-迭代法迭代次数为5次时对应的延拓结果,此时延拓得到的总强度磁异常最大值为318.95 nT,最小值为-145.47 nT,利用式(29)计算得到虚线框内延拓值与船载磁力测量值差值的中误差为6.14 nT (假若延拓方法本身无误差时,延拓值与船载磁力测量值差值中误差应为42 nT),验证了积分-迭代法具有较高的向下延拓精度。
|
| 图 3 积分-迭代法向下延拓结果 Fig. 3 Total field magnetic anomaly downward continuation using integral-iteration method |
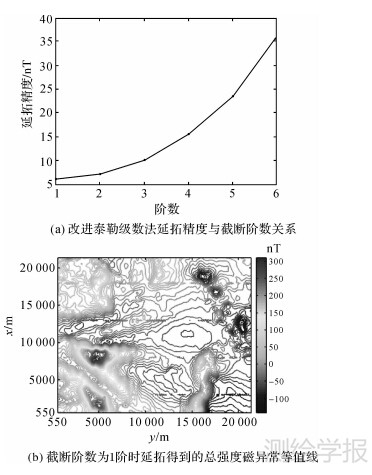
图 4是采用改进泰勒级数法将 z=195m高度的航空磁力测量总强度磁异常向下延拓至 z=0 m高度的结果。图 4(a)是不同截断阶数情况下改进泰勒级数法向下延拓值与船载磁力测量值差值中误差。受磁力测量值中含有误差的影响,改进泰勒级数法延拓精度随着截断阶数的增加而逐渐降低。当截断阶数为1阶时,总强度磁异常最大值为319.46nT,最小值为-146.72nT,利用式(29)计算得到的中误差为6.07nT,可以看到,改进泰勒级数法同样具有较高的向下延拓精度,且略高于积分—迭代法计算精度。当采用半余弦函数在测区4个方向上进行了10%扩边处理后,泰勒级数截断阶数为1阶时延拓值和船载磁力测量值差值中误差可进一步减小为5.98nT。
|
| 图 4 改进泰勒级数法计算结果 Fig. 4 Total field magnetic anomaly downward continuation using improved Taylor series |
4 结 论
(1) 研究表明,总强度磁异常近似满足拉普拉斯方程,其在无源空间内为准调和函数,且沿垂直方向的导数和积分同样为调和函数。
(2)向下延拓方法中的FFT法和常规泰勒级数法都存在较强的边界效应,且向下延拓深度越大,边界效应越明显;而积分-迭代法和提出的改进泰勒级数法同样存在一定程度边界效应。因此,在向下延拓某一测区磁场信息时,应尽可能使用于延拓的原始数据范围大于延拓后测区的范围;当两者范围相同且不能改变时,可采用半余弦扩边处理方案减弱边界效应的影响。
(3)试验数据验证表明,本文提出的方法实现了磁场稳健向下延拓,且计算精度略高于积分-迭代法计算精度。但由于积分-迭代法无法预知待延拓深度处磁场的真值,故其迭代次数无法预先准确确定,因而一定程度上制约了该方法的应用效果。而本文方法的限制性因素较少,具有更强的适用性。如果再结合扩边处理方案,改进泰勒级数向下延拓精度要略高于直接采用积分-迭代法。
(4)本文采用双三次样条函数计算了磁场在水平方向上的二阶导数,该方法对于无噪声或噪声水平较低的观测数据具有很高的精度。而观测数据中包含较强的高斯噪声时,利用三次样条函数得到的二阶导数精度有所降低。此时,可采用二阶中心差分方法计算磁场在水平方向上的二阶导数,经笔者验证效果较好。
| [1] | COOPER G. The Stable Downward Continuation of Potential Field Data[J]. Exploration Geophysics, 2004, 35(4): 260-265. |
| [2] | TROMPAT H, BOSCHETTI F, HORNBY P. Improved Downward Continuation of Potential Field Data[J]. Exploration Geophysics, 2003, 34(4): 249-256. |
| [3] | ROY A. Convergence in Downward Continuation for Some Simple Geometries[J]. Geophysics, 1967, 32(5): 853-866. |
| [4] | NING Jinsheng , WANG Haihong , LUO Zhicai. Downward Continuation of Gravity Signals Based on the Multiscale Edge Constraint[J]. Chinese Journal of Geophysics, 2005, 48(1): 63-68. (宁津生, 汪海洪, 罗志才. 基于多尺度边缘约束的重力场信号的向下延拓[J].地球物理学报, 2005, 48 (1): 63-68.) |
| [5] | PAWLOWSKI R S. Preferential Continuation for Potential-field Anomaly Enhancement[J]. Geophysics, 1995, 60(2): 390-398. |
| [6] | XU Shizhe. A Comparison of Effects between the Iteration Method and FFT for Downward Continuation of Potential Fields[J]. Chinese Journal of Geophysics, 2007, 50(1): 285-289. (徐世浙. 迭代法与FFT法位场向下延拓效果的比较[J]. 地球物理学报,2007, 50(1): 285-289.) |
| [7] | WANG Xingtao, SHI Pan, ZHU Feizhou. Regularization Methods and Spectral Decomposition for the Downward Continuation of Airborne Gravity Data[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(1): 33-38. (王兴涛, 石磐, 朱非洲. 航空重力测量数据向下延拓的正则化算法及其谱分解[J]. 测绘学报, 2004, 33(1): 33-38.) |
| [8] | XU Shizhe. The Integral-iteration Method for Continuation of Potential Fields[J]. Chinese Journal of Geophysics, 2006, 49(4): 1176-1182. (徐世浙. 位场延拓的积分-迭代法[J]. 地球物理学报, 2006, 49(4): 1176-1182.) |
| [9] | ZHANG Hui, CHEN Longwei, REN Zhixing, et al. Analysis on Convergence of Iteration Method for Potential Fields Downward Continuation and Research on Robust Downward Continuation Method[J]. Chinese Journal of Geophysics, 2009, 52(4): 1107-1113. (张辉, 陈龙伟, 任治新, 等. 位场向下延拓迭代法收敛性分析及稳健向下延拓方法研究[J]. 地球物理学报, 2009, 52(4): 1107-1113.). |
| [10] | EVJEN H M. The Place of the Vertical Gradient in Gravitational Interpretations[J]. Geophysics, 1976, 1(1): 127-136. |
| [11] | ZHAI Guojun, BIAN Guanglang, HUANG Motao, et al. A New Method to Calculate the Vertical Derivatives of Total Field Magnetic Anomaly[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 671-678. (翟国君,卞光浪,黄谟涛,等. 总强度磁异常各阶垂向导数换算新方法[J]. 测绘学报, 2011, 40(6):671-678.). |
| [12] | PETERS L J. The Direct Approach to Magnetic Interpretation and Its Practical Application[J]. Geophysics, 1949, 14(3): 290-320. |
| [13] | GUNN P J. Linear Transformations of Gravity and Magnetic Fields[J]. Geophysical Prospecting, 1975, 23(2): 300-312. |
| [14] | BIAN Guanglang, ZHAI Guojun, LIU Yanchun. Components Conversion of Magnetic Anomaly in Detecting Underwater Magnetic Object[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 163-168. (卞光浪, 翟国君, 刘雁春. 水下磁性目标探测中磁异常分量换算方法[J]. 测绘学报, 2011, 40(2): 163-168.). |
| [15] | BIAN Guanglang, ZHAI Guojun, LIU Yanchun, et al. Computation of Spatial Position Parameters of Magnetic Object with Improved Euler Approach[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(3): 386-392. (卞光浪, 翟国君, 刘雁春, 等. 应用改进欧拉算法解算磁性目标空间位置参数[J]. .测绘学报, 2011, 40(3): 386-392.). |
| [16] | GEROVSKA D, ARAúZO-BRAVO M J, STAVREV P. Determination of the Parameters of Compact Ferro-metallic Objects with Transforms of Magnitude Magnetic Anomalies[J]. Journal of Applied Geophysics, 2004, 55(3-4):173-186. |
| [17] | ZHANG Fengxu, MENG Lingshun, ZHANG Fengqin. A Study of Smoothing Filter Operator for Normalized Full Gradient of Gravity Anomaly in Wave Number Domain[J]. Geophysical & Geochemical Exploration, 2005, 29(3): 248-252. (张凤旭, 孟令顺, 张凤琴. 波数域重力归一化总梯度法中的圆滑滤波因子地球物理学报, 2009, 52(8): 2182-2188.) |
| [18] | YU Bo, ZHAI Guojun, LIU Yanchun, et al. Analysis of Noise Effect on the Calculation Error of Downward Continuation with Iteration Method[J]. Chinese Journal of Geophysics, 2009, 52(8): 2182-2188. (于波, 翟国君, 刘雁春, 等.噪声对磁场向下延拓迭代法的计算误差影响分析[J]. 地球物理学报, 2009, 52(8): 2182-2188.) |
| [19] | YU Bo, ZHAI Guojun, LIU Yanchun. The Downward Continuation Method of Aeromagnetic Data to the Sea Level[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(3): 202-209. (于波, 翟国君, 刘雁春. 利用航磁数据向下延拓得到海面磁场的方法[J]. 测绘学报, 2009, 38(3): 202-209.) |
| [20] | State Bureau of Quality and Technical Supervision. GB/T 13909—1992 Specification for Oceanographic Survey: Marine Geology and Geophysics[S]. Beijing: Standards Press of China, 1993. (国家质量监督检疫总局. GB/T 13909—1992 海洋调查规范: 海洋地质地球物理调查[S]. 北京: 标准出版社, 1993.) |