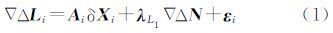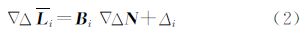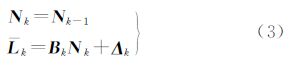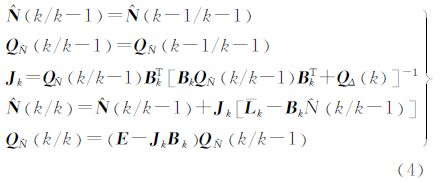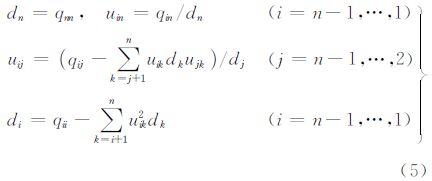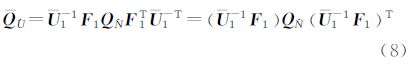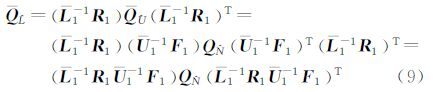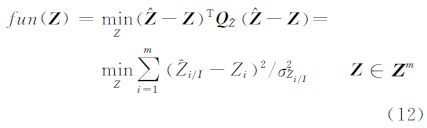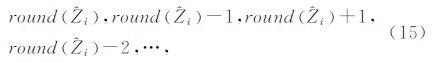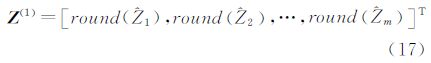1 前 言
利用GPS载波相位进行相对定位是高精度测量的有效手段,而双差相位观测值中模糊度的正确解算是实现厘米级或亚厘米级定位的关键问题,尤其是GPS动态定位中,对整周模糊度的快速解算显得更加重要[1, 2]。目前,国内外相关学者先后提出了多种整周模糊度的求解方法,如常用的快速模糊度确定法(FARA)[3]、模糊度最小二乘搜索法(LSAST)[4]、最小二乘降相关分解法(LAMBDA)[5, 6, 7]、模糊度估计的最优化法(OMEGA)[8]以及综合取整法和搜索法的优点所形成的模糊度动态快速固定方法(PBFAT)[9]等。上述多数算法是基于双频相位观测量提出的,在单频GPS动态定位情况下,这些方法往往需要较多历元的观测数据才能正确固定整周模糊度,并且在模糊度分解之前,需先通过最小二乘或卡尔曼滤波来估计包含坐标参数的实数解,从而使实数解解算所耗费的时间及计算量大大增加,无法满足快速定位的要求。针对这个问题,本文提出了一种适合单频GPS动态定位模糊度快速解算的方法,该方法通过QR分解变换消去观测方程中的坐标参数信息,利用Kalman滤波仅对模糊度参数进行估计,在滤波获取模糊度浮点解的基础上,基于排序和双Cholesky分解进行降相关处理,同时结合收缩搜索空间的思想固定整周模糊度。通过实例计算验证了该方法的正确性和有效性。
2 单频GPS动态定位中模糊度浮点解计算当分别安置在基准站和流动站的两台单频GPS接收机共视n+1颗卫星时,每一历元可组成n个相位双差观测方程,则对不同历元i建立线性化后的双差观测方程为[10]
式中,▽△Li是单频双差观测值向量,为双差实测值减去流动站近似位置求取的卫地距离双差值;Ai为双差方程的系数阵;δXi为坐标分量改正数组成的向量;▽△N为整周模糊度向量;εi为观测误差向量。由式(1)易知,该方程单个历元解算的秩亏数为3,利用最小二乘是无法正常求解的。常规的方法是增加历元数,使方程组个数多于未知量个数后,再进行求解。一般情况下,这种方法不仅需要较多历元(至少200个)的观测数据才能获取精度较优的模糊度浮点解,且利用最小二乘在解算法方程的过程中,会遇到高阶矩阵求逆的问题[11],从而使计算量很大,无法满足动态定位实时处理的要求。由于在动态相对定位整个解算过程的初始阶段,主要目的在于模糊度浮点解及其方差阵的求解,因此,为使解算中模糊度参数与坐标参数达到有效分离,通过对系数矩阵Ai实施QR分解[12],利用Q矩阵存在的特性对式(1)进行变换来消去坐标分量改正数向量δXi。整个分解变换过程按以下两步进行:(1) 利用Householder变换法对Ai进行QR分解,使Ai=QR,其中Q为n×n阶矩阵,R为n×3阶矩阵,并对分解后的Q矩阵进行分块处理,即
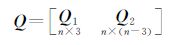
(2) 对分块子矩阵Q2进行转置,并利用转置矩阵Q2T左乘式(1)两边。由于存在关系式:Q2TAi 0,因此可得不含坐标分量改正数向量δXi的定位方程
0,因此可得不含坐标分量改正数向量δXi的定位方程
当每个历元观测相同的卫星时,考虑相位无周跳时整周模糊度存在相等的特性,并根据Kalman滤波器在动态系统数据处理中是无偏的最小方差估计等优点[13],对式(2)采用Kalman滤波进行重新建模。其系统的状态方程和观测方程为
式中Nk、Nk-1分别为tk历元和tk-1历元的模糊度参数向量,由于模糊度不随观测历元而发生变化,因此其动态噪声及其协方差阵都为零;Lk、Bk分别为tk历元的观测向量和观测矩阵;Δk为观测噪声、是均值为零且协方差阵为QΔ(k)的正态白噪声序列,Lk、Bk、Δk等价于式(2)在tk历元的各参数向量。则由式(3)组成的Kalman滤波方程递推公式为 式中,Jk为Kalman增益矩阵;E为单位矩阵。滤波的初始模糊度值 (0/0)由第一个历元的伪距双差方程求解出流动站的点位坐标后,再结合相位观测值反算求得;通常由此估计的模糊度初值含有较大的偏差,为使滤波较快地收敛,因此本文将初始方差
(0/0)由第一个历元的伪距双差方程求解出流动站的点位坐标后,再结合相位观测值反算求得;通常由此估计的模糊度初值含有较大的偏差,为使滤波较快地收敛,因此本文将初始方差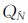 (0/0)取为4000。同时,根据式(3)~式(4)可知,该滤波方程只含有模糊度状态参数向量,不含坐标参数、速度参数等状态信息,因此相比方程式(1)降低了阶次,且减小了计算量,满足在动态定位中对模糊度进行实时估计的要求。
3 模糊度的降相关分解及搜索固定
3.1 基于排序和连续双Cholesky分解的模糊度降相关处理
(0/0)取为4000。同时,根据式(3)~式(4)可知,该滤波方程只含有模糊度状态参数向量,不含坐标参数、速度参数等状态信息,因此相比方程式(1)降低了阶次,且减小了计算量,满足在动态定位中对模糊度进行实时估计的要求。
3 模糊度的降相关分解及搜索固定
3.1 基于排序和连续双Cholesky分解的模糊度降相关处理利用式(3)~式(4)可实现对模糊度浮点解的实时解算。但在实际应用中,因为双差处理模式使模糊度浮点解间产生很大的相关性,所以模糊度的方差阵不为对角阵。同时,基于模糊度方差阵所构造的模糊度搜索空间是一个超椭球区域,其形状因模糊度间的强相关性而被拉得过于扁长,造成整周模糊度解的搜索效果很差,为此需对模糊度浮点解及其方差阵进行空间分解变换运算,以降低模糊度间的相关性。由于下三角Cholesky(即LDTT)分解可将相关矩阵变为不相关矩阵[14, 15],因此也可通过对模糊度方差阵连续进行上三角Cholesky(即UDUT)分解和下三角Cholesky分解来达到降相关的目的[16, 17]。
由矩阵分解理论可知,对n阶(n≥2)对称正定矩阵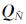 进行UDUT分解是唯一的,其中U是单位上三角阵,D是对角元全为正的对角阵。相应的计算公式为
进行UDUT分解是唯一的,其中U是单位上三角阵,D是对角元全为正的对角阵。相应的计算公式为
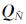 对应的元素;di为对角阵D对应的元素。通过分析式(5)可知,由于di>0,因此
对应的元素;di为对角阵D对应的元素。通过分析式(5)可知,由于di>0,因此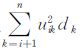 为多个正数求和,且随着i值的减少,其值将不断增大,为此在计算di的过程中,需使qii减小更大的量才能得到全为正值的对角元素。若使式(5)中较大的qii所对应的下标i值较小,或使较小的qii所对应的下标i值较大,再对矩阵
为多个正数求和,且随着i值的减少,其值将不断增大,为此在计算di的过程中,需使qii减小更大的量才能得到全为正值的对角元素。若使式(5)中较大的qii所对应的下标i值较小,或使较小的qii所对应的下标i值较大,再对矩阵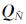 进行上三角Cholesky分解,则分解得到的对角阵D中对应元素di间的差距将减小,从而使矩阵D的条件数变小。因此通过对矩阵
进行上三角Cholesky分解,则分解得到的对角阵D中对应元素di间的差距将减小,从而使矩阵D的条件数变小。因此通过对矩阵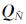 进行降序排列,也就是将矩阵
进行降序排列,也就是将矩阵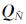 的对角线元素按照从大到小的顺序进行调整后,再进行上三角Cholesky分解来达到改善矩阵分解的效果。设原矩阵
的对角线元素按照从大到小的顺序进行调整后,再进行上三角Cholesky分解来达到改善矩阵分解的效果。设原矩阵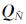 降序调整后得到的新矩阵为QF,则转换前后两矩阵之间存在如下关系式
式中,F为降序调整矩阵。其形成的过程为:记录矩阵
降序调整后得到的新矩阵为QF,则转换前后两矩阵之间存在如下关系式
式中,F为降序调整矩阵。其形成的过程为:记录矩阵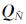 中每个对角元素按降序排列后在原矩阵
中每个对角元素按降序排列后在原矩阵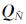 中所对应的位置m,若矩阵F中对应元素fij的下标j存在j=m,则令fij=1,否则令fij=0,依次循环计算便可生成和矩阵
中所对应的位置m,若矩阵F中对应元素fij的下标j存在j=m,则令fij=1,否则令fij=0,依次循环计算便可生成和矩阵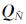 同维大小的n阶降序调整矩阵F。
同维大小的n阶降序调整矩阵F。
此外,在对矩阵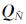 进行上三角Cholesky分解后,需继续对整数可逆变换后的方差阵
进行上三角Cholesky分解后,需继续对整数可逆变换后的方差阵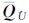 进行下三角Cholesky分解。其计算公式为
进行下三角Cholesky分解。其计算公式为
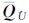 对应的元素;dj为对角阵D对应的元素,且dj>0。通过比较式(5)、式(7)可以发现,对矩阵进行上三角Cholesky分解和下三角Cholesky分解是互为逆向的分解过程,因此,基于与上述上三角Cholesky分解同样的分析原理,为了让下三角Cholesky分解变换后对角阵D的条件数变小,可使
对应的元素;dj为对角阵D对应的元素,且dj>0。通过比较式(5)、式(7)可以发现,对矩阵进行上三角Cholesky分解和下三角Cholesky分解是互为逆向的分解过程,因此,基于与上述上三角Cholesky分解同样的分析原理,为了让下三角Cholesky分解变换后对角阵D的条件数变小,可使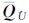 中较大的对角线元素qjj对应较大的j值,或使较小的对角线元素qjj对应较小的j值,也就是利用升序调整矩阵R对矩阵
中较大的对角线元素qjj对应较大的j值,或使较小的对角线元素qjj对应较小的j值,也就是利用升序调整矩阵R对矩阵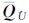 进行调整变换,从而使转换后新矩阵中对角线元素的值满足依次从小到大的规律。
进行调整变换,从而使转换后新矩阵中对角线元素的值满足依次从小到大的规律。
综合以上所述,利用排序和连续双Cholesky分解对模糊度方差阵进行降相关处理的具体步骤为:
(1) 利用降序调整矩阵F1对模糊度方差阵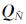 进行变换,即
进行变换,即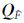 =F1
=F1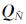 F1T,并对
F1T,并对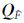 作上三角Cholesky分解,使
作上三角Cholesky分解,使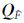 =U1D1U1T;
=U1D1U1T;
(2) 对上三角阵U1取整后,再求逆得到整数变换阵U1-1,利用U1-1可计算整数变换后的方差阵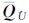 为
为
(3) 采用升序调整矩阵R1对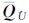 进行重新排序得到矩阵
进行重新排序得到矩阵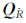 =R1
=R1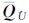 R1T后,再对
R1T后,再对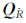 作下三角Cholesky分解,得到
作下三角Cholesky分解,得到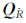 =L1D1L1T;
=L1D1L1T;
(4) 同样对下三角阵L1取整后再求逆,得到变换阵L1-1,然后计算变换后的方差阵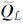 ,其经过恒等变换的表达式为
,其经过恒等变换的表达式为
(5) 检查矩阵L1-1是否为单位矩阵,若是,则结束分解;否则,将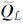 赋值给
赋值给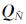 ,继续计算上述(1)~(4)步,直到L1-1为单位阵为止。
,继续计算上述(1)~(4)步,直到L1-1为单位阵为止。
基于以上计算步骤,当进行了k步迭代,且检验L1-1为单位阵时,则最终得到的整数可逆模糊度变换阵为
相应的,通过T矩阵变换可得到降相关后的模糊度方差阵及模糊度浮点解为
3.2 整周模糊度的搜索固定经过上述整数可逆模糊度变换后,整周模糊度的最小二乘估计目标函数可写为
由于在实际的计算当中,解决式(12)的最小二乘问题是通过离散搜索来实现的,因此,基于上式来构造的模糊度搜索空间可表示为
显然,由式(13)所确定的搜索空间是一个m维超椭球,而模糊度的每个整数解就是在这个超椭球区域通过序贯约束条件来搜索获取的,此序贯约束条件如下式所示
综合式(12)~式(14)便形成了LAMBDA法中的整数最小二乘搜索方法,通过对LAMBDA的搜索算法进行分析可知,χ2的取值控制着超椭球区域的体积,且在整个搜索的过程中,超椭球的体积保持不变。文献[18]指出,收缩超椭球体积大大有益于整周模糊度的搜索处理,可改善搜索处理过程[18]。然而,这种搜索思想在LAMBDA的搜索算法中却未得到很好的体现。因此,为了搜索到最优的整数最小二乘解并改善LAMBDA的搜索过程,只要在搜索区域内找到一个候选整数向量Z,就将其相对应的目标函数fun(Z)作为χ2的一个新值,以此来缩小搜索区域[19, 20]。对模糊度应用此思想进行搜索处理的具体过程如下:
首先,假定需得到p个候选整数向量,在初始时刻设置χ2等于无穷大。不同于LAMBDA算法对搜索区间进行从小到大的直接搜索法,而是在第i个搜索区间(由模糊度Zi的上限和下限组成),以距离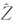 i单调递增的整数值来进行搜索,即如果
i单调递增的整数值来进行搜索,即如果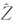 i≤round(
i≤round(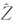 i),使用以下搜索序列
i),使用以下搜索序列
其次,令第2个候选向量Z(2)中的第1个元素取次接近于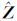 1的整数值,Z(2)的其他元素与Z(1)中的相等,同时,第3个候选向量Z(3)中的第1个元素取第三接近于
1的整数值,Z(2)的其他元素与Z(1)中的相等,同时,第3个候选向量Z(3)中的第1个元素取第三接近于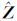 1的整数值,其余元素与Z(1)中的一致,依此类推可得p个候选整数向量Z(1)、Z(2)、…、Z(p),显而易见存在关系式f(Z(1))≤f(Z(2))…≤f(Z(p)),并通过设置χ2=f(Z(p))使椭球区域收缩减小。继续搜索新的有效整数候选向量,直到在第m个搜索区间找到一个新的候选向量,并用这个新的候选向量来代替使f(Z(j))=χ2的候选向量Z(j),进一步缩小椭球区域,且让新的χ2的值满足χ2=
1的整数值,其余元素与Z(1)中的一致,依此类推可得p个候选整数向量Z(1)、Z(2)、…、Z(p),显而易见存在关系式f(Z(1))≤f(Z(2))…≤f(Z(p)),并通过设置χ2=f(Z(p))使椭球区域收缩减小。继续搜索新的有效整数候选向量,直到在第m个搜索区间找到一个新的候选向量,并用这个新的候选向量来代替使f(Z(j))=χ2的候选向量Z(j),进一步缩小椭球区域,且让新的χ2的值满足χ2=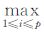 (fZ(i))。
(fZ(i))。
最后,继续上述搜索处理过程,当直到无法再找到一个新的有效整数候选向量时,则停止搜索并最终得到p个最优整数最小二乘估计值。
4 实例分析本文算例中的试验数据是在西南交通大学犀浦校区实测得到的,数据采集时间为2011年7月15日。在获取该数据的试验过程中,采用一台中海达V8 GNSS双频接收机作为基准站,另一台V8 GNSS双频接收机作为流动站进行动态观测,基准站和流动站的采样率都设为1 s,连续跟踪8颗GPS卫星,共计采集动态数据1333个历元。利用GAMIT软件中的动态定位模块TRACK解算这段数据,得到流动站每个历元的三维坐标[X,Y,Z]T,并求得流动站到基准站的最短基线长度为34.904 0 m、最长基线长度为183.458 8 m。其流动站的运动轨迹和基准站的点位如图 1所示。
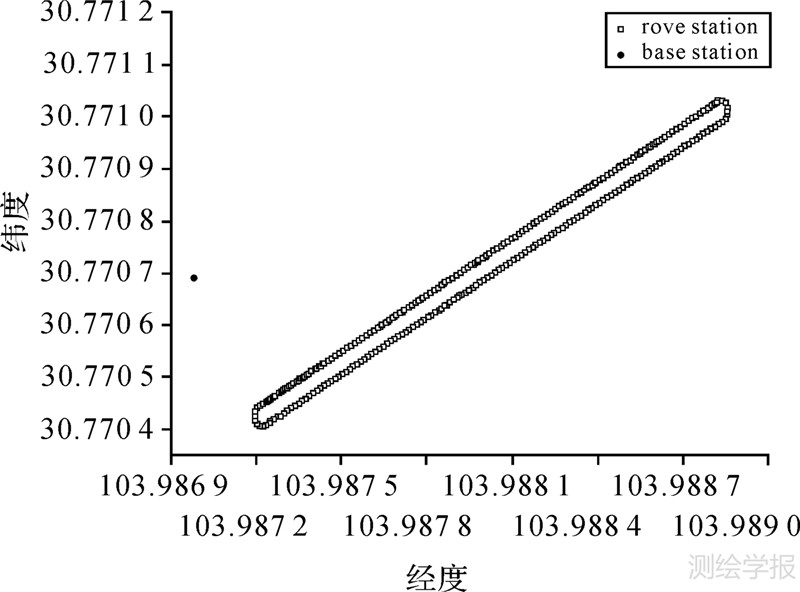
|
| 图 1 流动站的运动轨迹和基准站的点位 Fig. 1 Rove station motion curve and base station point location |
根据文中提出的单频GPS整周模糊度快速解算新方法,仅利用上述动态数据中L1频率的相位观测值逐个历元进行求解,将其所求结果与TRACK解算的标准值求差并作比较,可得流动站各历元X、Y、Z 3个方向的坐标真误差序列如图 2所示。
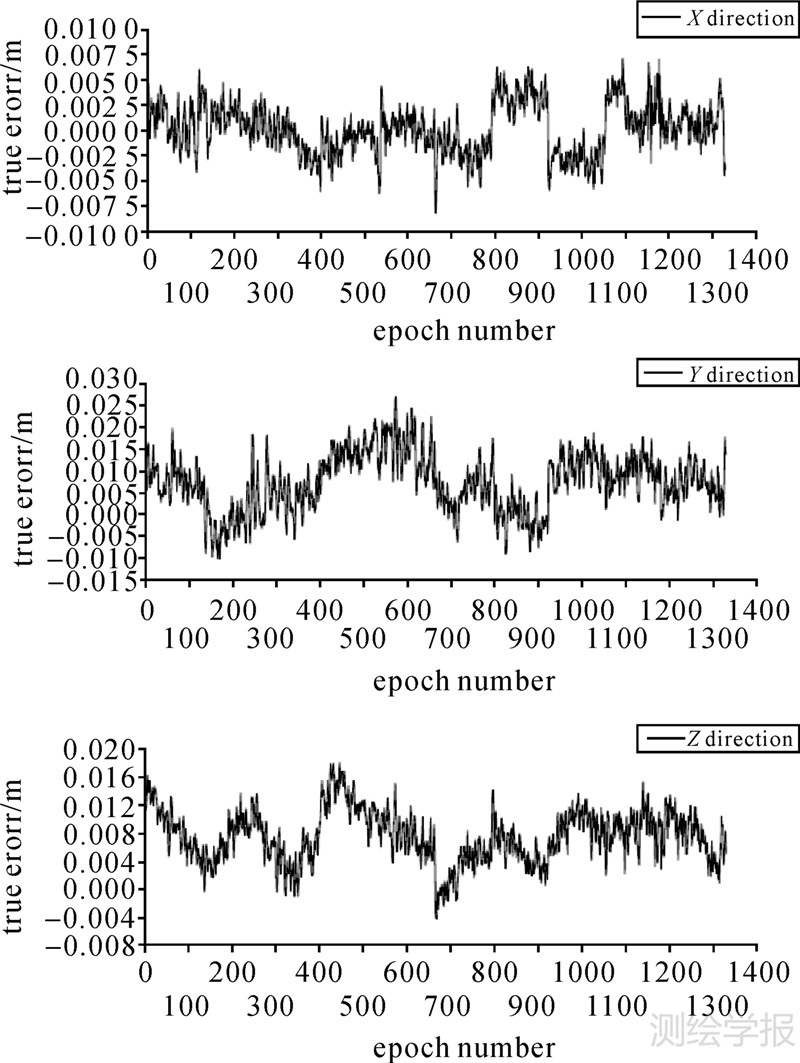
|
| 图 2 流动站X、Y、Z方向的坐标真误差序列 Fig. 2 Coordinates true error of rove station in X,Y,Z direction |
从图 2可以看出,X、Y、Z 3个方向的坐标真误差值最大处历元所对应的值分别小于1 cm、3 cm和2 cm,且所有历元整体的坐标真误差值较小,由此表明模糊度被正确固定。同时,统计了该算法求解流动站坐标的定位精度,3个方向的解算精度分别为:σX=±2.5 mm、σY=±9.2 mm、σZ=±8.3 mm,验证了该算法的正确性和有效性。
另一方面,以试验数据中L1单频相位组成的双差卫星对[14-31,16-31,25-31,29-31,20-31,22-31,32-31]所对应的整周模糊度真值N=[0,-5,4,6,5,2,-1]为参考值,分析该算法利用Kalman滤波器来求解模糊度浮点解的效果。所有卫星对的模糊度浮点解如图 3所示。

|
| 图 3 所有卫星对的模糊度浮点解 Fig. 3 Ambiguity float solution of all satellites |
从图 3中可以看出,所有卫星对的模糊度浮点解在临近历元数为200时呈现近似于真值的趋势,且滤波器开始趋于稳定状态。同时,对不同历元数的数据单元分别采用本文方法与常规Kalman滤波方法进行求解,选取其中以历元数200为临界点、部分连续历元两种方法的计算结果比较列于表 1。
| 历元 | 模糊度浮点解与真值的差 | -N| -N|
| |
| 本文提出的方法 | 常规Kalman滤波方法 | |
| 197 | 0.019,0.466,0.055,0.057,0.249,0.436,0.187 | 0.123,0.636,0.829,1.604,0.332,0.232,1.360 |
| 198 | 0.011,0.456,0.067,0.038,0.243,0.421,0.186 | 0.124,0.637,0.829,1.604,0.333,0.231,1.361 |
| 199 | 0.014,0.454,0.071,0.036,0.232,0.419,0.182 | 0.125,0.637,0.827,1.603,0.334,0.230,1.362 |
| 200 | 0.049,0.456,0.041,0.087,0.213,0.447,0.163 | 0.126,0.638,0.826,1.602,0.335,0.229,1.363 |
| 201 | 0.013,0.431,0.070,0.033,0.220,0.399,0.173 | 0.127,0.639,0.825,1.601,0.336,0.228,1.364 |
| 202 | 0.018,0.420,0.073,0.031,0.201,0.392,0.162 | 0.128,0.640,0.824,1.600,0.336,0.227,1.365 |
| 203 | 0.083,0.417,0.022,0.117,0.151,0.435,0.121 | 0.129,0.641,0.823,1.599,0.337,0.226,1.366 |
由表 1可知,在单频GPS动态定位情况下,利用本文方法求解的模糊度浮点解精度优于常规Kalman滤波方法。此外,分别统计了表 1所列历元两种方法的平均计算时间,本文方法为1004 ms、常规Kalman滤波方法为1440 ms,究其原因在于常规Kalman滤波方法需同时估计坐标参数、速度参数及模糊度参数,而本文方法通过对系数阵QR分解消去坐标参数来改善方程的状态,从而形成仅含模糊度参数的Kalman滤波模型进行求解,这样既提高了计算速度,又改善了模糊度浮点解的精度,有利于整周模糊度的快速准确解算。
随后,对Kalman滤波求解得到的模糊度方差阵作降相关处理分析,以评价该算法的降相关程度。表 2列出了其中连续15个历元模糊度方差阵降相关前后的各参数信息。从表 2可以看出,降相关前基于方差阵的搜索椭球各轴相差悬殊,椭球的扁率e很大,表明模糊度间是强相关的;而降相关后椭球各轴变得较为均匀,椭球的扁率大大减小,且降相关系数r值明显增大,说明该算法在方差阵降相关处理时具有很好的适用性,可获得良好的降相关效果。
| 历元序号 | 降相关前 | 降相关后 | ||||||
| λmax | λmin | e | r | λmax | λmin | e | r | |
| 1 | 434.052 | 0.004 73 | 91 765.751 | 9.738×10-9 | 0.778 | 0.110 | 7.072 | 0.673 |
| 2 | 431.068 | 0.004 72 | 91 327.966 | 9.824×10-9 | 0.772 | 0.109 | 7.082 | 0.674 |
| 3 | 428.108 | 0.004 71 | 90 893.418 | 9.910×10-9 | 0.767 | 0.108 | 7.102 | 0.675 |
| 4 | 425.174 | 0.004 69 | 90 655.437 | 9.997×10-9 | 0.761 | 0.108 | 7.046 | 0.676 |
| 5 | 422.265 | 0.004 68 | 90 227.564 | 1.008×10-8 | 0.756 | 0.107 | 7.065 | 0.677 |
| 6 | 419.381 | 0.004 67 | 89 803.212 | 1.017×10-8 | 0.750 | 0.106 | 7.075 | 0.677 |
| 7 | 416.521 | 0.004 66 | 89 382.189 | 1.026×10-8 | 0.745 | 0.106 | 7.028 | 0.678 |
| 8 | 413.685 | 0.004 65 | 88 964.516 | 1.035×10-8 | 0.740 | 0.105 | 7.048 | 0.679 |
| 9 | 410.873 | 0.004 64 | 88 550.216 | 1.044×10-8 | 0.735 | 0.104 | 7.067 | 0.679 |
| 10 | 408.084 | 0.004 62 | 88 329.870 | 1.053×10-8 | 0.729 | 0.104 | 7.001 | 0.680 |
| 11 | 405.319 | 0.004 61 | 87 921.692 | 1.062×10-8 | 0.724 | 0.103 | 7.029 | 0.681 |
| 12 | 402.578 | 0.004 60 | 87 516.957 | 1.072×10-8 | 0.719 | 0.102 | 7.049 | 0.681 |
| 13 | 399.859 | 0.004 59 | 87 115.251 | 1.081×10-8 | 0.715 | 0.102 | 7.010 | 0.682 |
| 14 | 397.164 | 0.004 58 | 86 717.031 | 1.091×10-8 | 0.710 | 0.101 | 7.030 | 0.682 |
| 15 | 394.490 | 0.004 57 | 86 321.663 | 1.100×10-8 | 0.705 | 0.100 | 7.050 | 0.682 |
(1) 通过对实测的动态数据分析表明,应用本文提出的方法在短基线下来解算单频GPS整周模糊度是正确和有效的。
(2) 对双差定位方程中坐标参数的系数阵实施QR分解并作相应的变换,在消去坐标参数信息的同时改善了方程的状态,建立仅含模糊度未知数的Kalman滤波递推方程进行求解,不但减小了计算量,而且有利于实现整周模糊度的快速解算。
(3) 在模糊度方差阵的连续双Cholesky分解过程中,对模糊度方差阵分别进行降序和升序处理后再作分解变换,可实现模糊度搜索空间的最大不相关,进而有利于提高整周模糊度的搜索效率。
| [1] | HOFMANN-WELLENHOF B, LICHTENEGGER H,COLLINS J. Global Positioning System: Theory and Practice[M]. 5th ed. New York: Springer Wien, 2001. |
| [2] | XU G C. GPS Theory: Algorithms and Applications[M]. 2nd ed. Berlin: Springer-Verlag,2007. |
| [3] | FREI E, BEUTLER G. Rapid Static Positioning Based on the Fast Ambiguity Resolution Approach “FARA”: Theory and First Results[J]. Manuscripta Geodaetica,1990, 15(4): 325-356. |
| [4] | HATCH R. Instantaneous Ambiguity Resolution[C]//IAG Symposia Proceedings of Kinematic Systems in Geodesy, Surveying, and Remote Sensing: 107.New York: Springer,1990: 299-308. |
| [5] | TEUNISSEN P J G. A New Method for Fast Carrier Phase Ambiguity Estimation[C]//Proceedings IEEE Position, Location and Navigation Symposium PLANS’94. Las Vegas: IEEE,1994:562-573. |
| [6] | TEUNISSEN P J G. The Invertible GPS Ambiguity Transformation[J]. Manuscripta Geodaetica, 1995, 20(6): 489-497. |
| [7] | TEUNISSEN P J G.The Least-squares Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy, 1995, 70(1/2): 65-82. |
| [8] | KIM D, LANGLEY R B. An Optimized Least-squares Technique for Improving Ambiguity Resolution and Computational Efficiency[C]// Proceedings of ION GPS-99: 12th International Technical Meeting of the Satellite Division of The Institute of Navigation. Nashville: ION, 1999: 1579-1588. |
| [9] | XIONG Yongliang, HUANG Dingfa, ZHANG Xianzhou, et al. Fast Algorithm for Kinematic GPS Data Processing Based on Invertible Integer Ambiguity Transformation and Probability Computation[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(3): 211-216. (熊永良, 黄丁发, 张献洲, 等. 基于整数可逆模糊度变换和概率计算的GPS动态数据处理快速算法[J]. 测绘学报, 2002, 31(3): 211-216.) |
| [10] | WANG Zhenjie, OU Jikun, LIU Lintao. Investigation on Solutions of Ill-conditioned Problems in Rapid Positioning Using Single Frequency GPS Receivers[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(3): 196-201. (王振杰, 欧吉坤, 柳林涛. 单频GPS快速定位中病态问题的解法研究[J]. 测绘学报, 2005, 34(3): 196-201 |
| [11] | YU Guorong. Full-cycle Ambiguity Resolution of Kinematical-to-Kinematical[J]. China Railway Science, 2003, 24(4): 40-44. (喻国荣. 动对动GPS相对定位系统中整周模糊度求解[J]. 中国铁道科学, 2003, 24(4): 40-44.) |
| [12] | LIU Lilong, LIU Jiyu, LI Guangcheng. Rapid Ambiguity Resolution On-the-fly for Single Frequency Receiver[J]. Geomatics and Information Science of Wuhan University 2005, 30(10): 885-887. (刘立龙, 刘基余, 李光成. 单频GPS整周模糊度动态快速求解的研究[J]. 武汉大学学报: 信息科学版, 2005, 30(10): 885-887.) |
| [13] | CUI Xizhang, YU Zongchou, LIU Dajie, et al. Generalized Surveying Adjustment[M]. Wuhan: Wuhan University Press, 2006. (崔希璋, 於宗俦, 刘大杰, 等. 广义测量平差[M]. 武汉: 武汉大学出版社, 2006.) |
| [14] | XU P L. Random Simulation and GPS Decorrelation[J]. Journal of Geodesy, 2001, 75(7/8): 408-423. |
| [15] | CHEN S X, WANG Y S, DENG Y. A Rapid Algorithm for GPS Ambiguity Decorrelation[C]// Proceedings of the IEEE 5th International Conference on Intelligent Transportation Systems. Singapore: IEEE, 2002: 904-909. |
| [16] | MOHAMED A H, SCHWARZ K P. A Simple and Economical Algorithm for GPS Ambiguity Resolution on the Fly Using a Whitening Filter[J]. Navigation,1998, 45(3): 221-231. |
| [17] | HUANG Zhangyu, CHEN Sujuan. Modified GPS Ambiguity White-filtering Algorithm[J]. Journal of Southwest Jiaotong University, 2010, 45(1): 150-155. (黄张裕, 陈苏娟. 一种改进的GPS模糊度白化滤波算法[J]. 西南交通大学学报, 2010, 45(1): 150-155.) |
| [18] | JONGE P de,TIBERIUS C.The LAMBDA Method for Integer Ambiguity Estimation: Implementation Aspects[C]// Delft Geodetic Computing Center LGR-Series:12. Delft: Delft University of Technology, 1996:1-49. |
| [19] | CHANG X W, YANG X, ZHOU T. MLAMBDA: A Modified LAMBDA Method for Integer Least-squares Estimation[J]. Journal of Geodesy, 2005, 9(9): 552-565. |
| [20] | HUANG Zhangyu, LIU Shengnan, CHEN Sujuan. Modified Space Searching Algorithm for GPS Ambiguity[J]. Journal of Hehai University: Natural Sciences, 2011, 39(1): 89-94. (黄张裕, 刘胜男, 陈苏娟. 一种改进的GPS模糊度空间搜索算法[J]. 河海大学学报: 自然科学版, 2011, 39(1): 89-94.) |