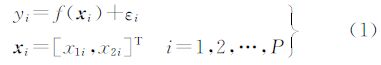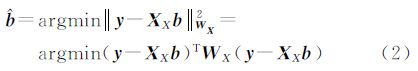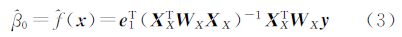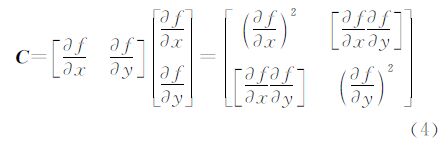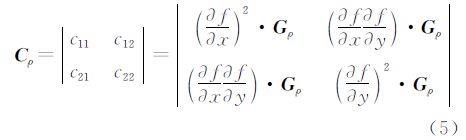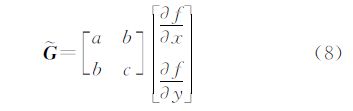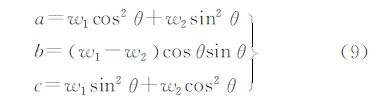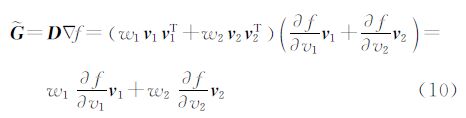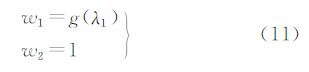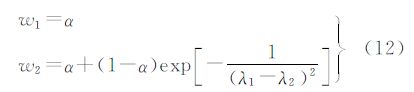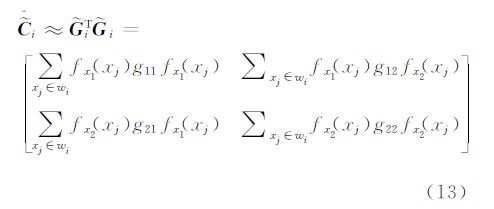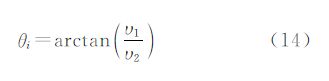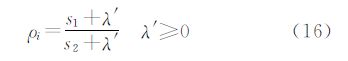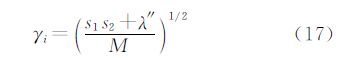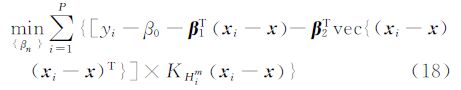2. 信息工程大学 理学院,河南 郑州 450001
2. Institute of Science, Information and Engineering University, Zhengzhou 450001, China
1 引 言
SAR系统是一种相干成像系统[1, 2]。在一定条件下,大量散射点的相干回波随机干涉,将在图像上出现相干斑。相干斑降低了系统对目标的分辨能力,减少了边缘检测、图像分割、目标分类等信息扩展技术的有效性,使SAR图像解译工作复杂化。因此,相干斑抑制是SAR图像处理的重要环节。
核方法已经广泛地应用于计算机领域,并且频繁地出现在解决模式检测和模式识别问题上[3, 4]。相比于其他参数估计方法,核回归作为一种非参数估计方法[5],它基于数据本身来定义模型的结构,这一优点从机理上保证了核回归方法的适用范围的广泛性。核回归在图像和视频处理中也有一定的应用[6, 7],但是并没有得到广泛的认可。事实上,图像处理技术中的二次卷积[8]、双边滤波器[9]、边缘插值[10]以及移动最小平方[11]等方法与核回归理论都紧密相关。
SAR图像相干斑抑制技术可以分为两大类:成像前的多视平滑预处理技术和成像后的滤波处理技术。其中,成像后的滤波技术包括空间滤波技术[12, 13, 14]和变换域滤波技术[15, 16]。虽然现有的相干斑抑制方法已有很多[17],并且针对某类图像也取得较好的处理效果,但由于核回归方法特有的性质,使得利用该方法进行图像去噪仍是值得关注的,在理论和应用上都具有很大的研究意义。
2 核回归方法假设二维SAR图像信号的数据测量模型如下
式中,f(xi)是回归函数;yi表示坐标点xi处的像素值;εi是独立同分布零均值白噪声;P表示邻域中采样点的个数。
对于大多数满足稀疏性的SAR图像而言,占其主要成分的背景中包含的大都是相干斑,而且由于SAR图像处理中主要关心的是目标特征,对背景部分只需保留其阴影和边缘特征,可用分片阶跃平面来逼近背景部分,因此,可用分片Taylor级数来表示图像[18]。假设xi是x附近的采样点,则有相应的2阶Taylor级数为
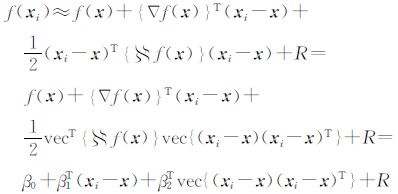
式中,▽和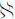 是梯度2×1和Hessian 2×2算子;β0=f(x);β1=▽ f(x)=
是梯度2×1和Hessian 2×2算子;β0=f(x);β1=▽ f(x)=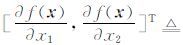 [β11,β12]T;β2=
[β11,β12]T;β2=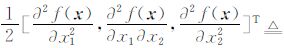 1/2[β21,β22,β23]T;vec是向量化算子,定义为一个对称矩阵的“下三角”部分的半向量化算子[5](它按一定顺序将一个矩形转换为一个向量);R为Taylor余项。从而可知β0正是需要估计的图像像素值,参数β1、β2给出了回归函数1阶和2阶微分估计。
1/2[β21,β22,β23]T;vec是向量化算子,定义为一个对称矩阵的“下三角”部分的半向量化算子[5](它按一定顺序将一个矩形转换为一个向量);R为Taylor余项。从而可知β0正是需要估计的图像像素值,参数β1、β2给出了回归函数1阶和2阶微分估计。
由于这个方法是基于局部近似的,相应的,需要为各个采样点对给定点的影响定义不同的权,相比于距离远的采样点,对与给定点距离近的采样点给以更高的权重,从而建立最优问题
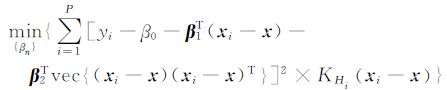
式中,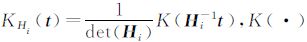 是关于y轴对称并在零点取最大值的二维高斯核函数,用来控制各个采样点的权重。Hi是2×2平滑矩阵,用来控制核函数的尺寸[10]。并且优化问题进一步写成加权最小二乘法的矩阵形式[14]
是关于y轴对称并在零点取最大值的二维高斯核函数,用来控制各个采样点的权重。Hi是2×2平滑矩阵,用来控制核函数的尺寸[10]。并且优化问题进一步写成加权最小二乘法的矩阵形式[14]
式中,
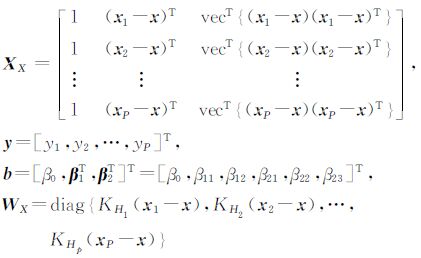
其最小平方估计为
这里,e1=[1 0 0 0 0 0]T。由式(3)可以看出,图像像素估计值本质上就是一个局部线性滤波器。
文献[15]中总结出以下3种类型的核函数。
(1) 经典核函数
KHi(xi-x),其中,Hi=hI
式中,h为全局平滑参数,此时得到的就是经典局部线性核回归算法。这种方法仅仅利用了空间信息,在图像平滑区域可以获得近似最佳的滤波效果,但对图像边缘继续估计时,容易造成边缘模糊。因此,有必要对经典的核回归算法进行改进,以达到更好的去噪效果。
(2)双边核函数
KHi(xi-x)Khr(yi-y),其中,Hi=hI
式中,h和hr分别是空间平滑参数和灰度平滑参数。将像素灰度值也引入核函数,即核函数分解为空间核及灰度核。但是对噪声比较严重的数据,由于灰度差别都很大,导致灰度权趋于0,达不到引入灰度核的效果。
(3)自适应核函数
KHisteer(xi-x),其中,Histeer=hCi1/2
式中,Histeer称为引导核,而对协方差矩阵Ci的估计为
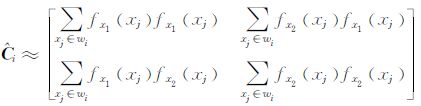
fx1(·)和fx2(·)分别为沿着x1和x2方向的梯度;wi为兴趣点附近的局部分析窗。自适应核的优点在于利用了图像局部结构信息,而不是仅仅利用灰度值。与此同时,引入正则化局部方向估计,使得自适应核回归方法较前两种方法去噪能力更强。
3 SAR图像先验信息SAR图像处理的前提是,对其成像过程中所蕴含的先验信息进行合理利用,所以对成像背景的研究和对先验信息的开采直接决定了模型的构建[18]。因此,在研究噪声抑制之前,对SAR图像所蕴含的先验信息进行挖掘。
3.1 针对点目标的先验信息利用自适应核回归方法抑制噪声时[5],其自适应核是以SAR图像的梯度特征为依据的,这虽然能在大体上区分图像的边缘区域和背景区域,但是除了边缘与背景外,SAR图像更需要区分目标点与背景。而这种基于梯度值的方法在目标区域内部不具有识别性。当点目标密集分布时,该方法就不能正确地区分图像的目标区域与背景区域。
根据SAR成像背景,在背景处图像幅值很小,几乎接近于0;同时,在目标处的幅值却很大[18],因此考虑将SAR图像的幅度信息引入核函数。
图 1(a)给出了某坦克的MSTAR图像,图 1(b)给出了幅度经过排序后的曲线图,从中可以看出,阴影区的图像幅度值最小,背景区其次,目标区最大,并且在阴影区与背景区之间和背景区与目标区之间分别存在一个明显的分界点。因此利用图像的幅度信息可以很好地标记图像的各种不同特征[18]。
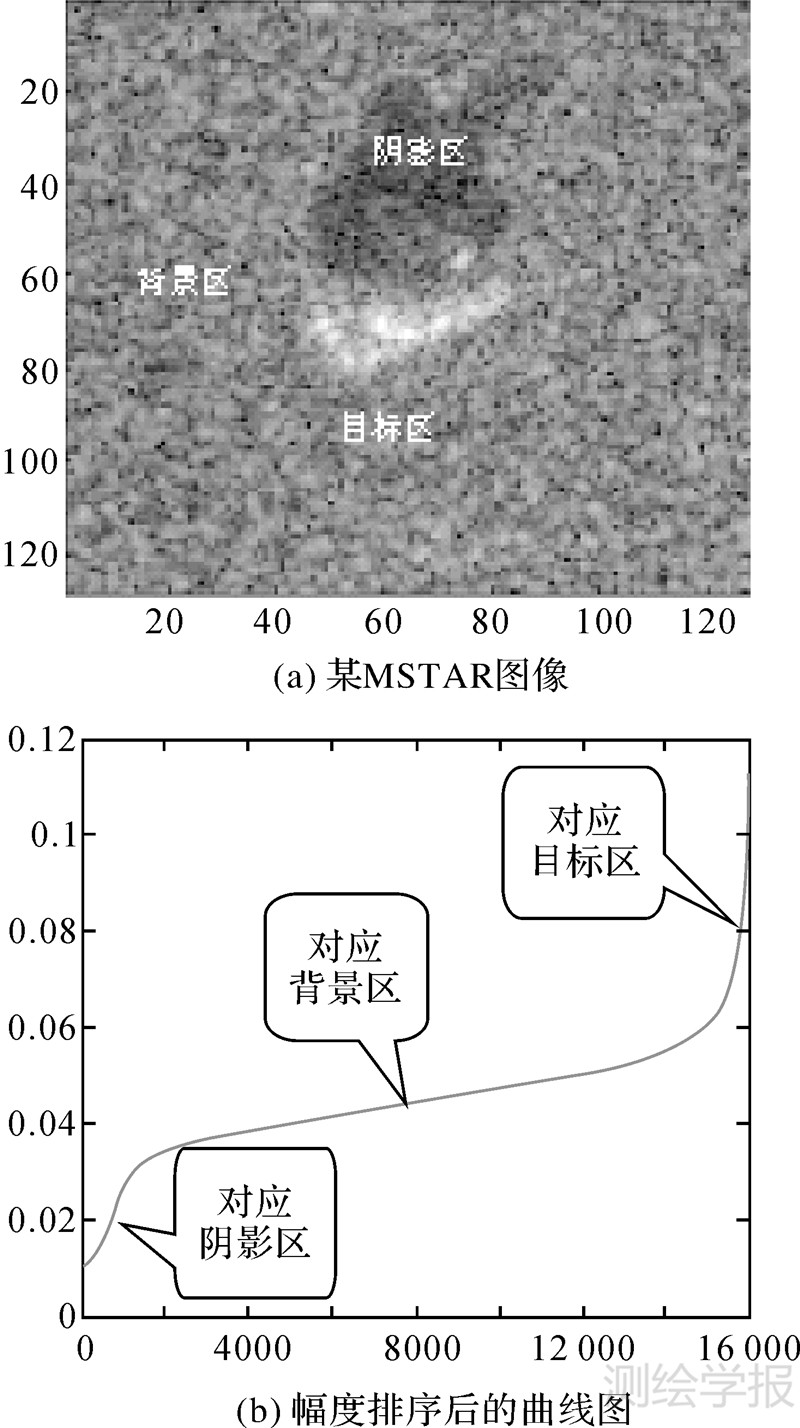
|
| 图 1 某MSTAR图像及其幅度排序后的曲线图 Fig. 1 The MSTAR image and its Sorted amplitude distribution |
所以,在构建模型时,将图像的幅度值引入核函数,也就是说,选择的自适应核函数是包含了图像幅度值变量和梯度值变量。
3.2 针对边缘目标的先验信息利用自适应核回归方法抑制噪声时[5],其自适应核的协方差矩阵为
式中,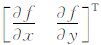 为梯度向量,可知协方差矩阵只有一个非零特征值λ1=(∂f/∂x)2+(∂f/∂y)2=|▽f|2,它对应的特征向量就是归一化的梯度矢量,即v1=▽f/|▽f|=η。由此可知,从协方差矩阵中得到的图像局部结构信息只有图像梯度。
为梯度向量,可知协方差矩阵只有一个非零特征值λ1=(∂f/∂x)2+(∂f/∂y)2=|▽f|2,它对应的特征向量就是归一化的梯度矢量,即v1=▽f/|▽f|=η。由此可知,从协方差矩阵中得到的图像局部结构信息只有图像梯度。
然而,图像的局部结构信息并不仅仅表现为图像的梯度。考虑利用如下定义的散射矩阵 (scatter matrix),可以获取更丰富的局部结构信息[19, 20]
式中,Gρ表示以ρ为参数的高斯核,Cρ的两个特征值分别为
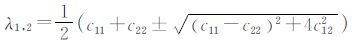
约定λ1>λ2。它们对应的特征向量分别为v1、v2,有
vi=(cosθi sinθi) i=1,2
且θ1=1/2arctan(2c12/c11-c22),θ2=θ1+π/2。
分析其特征值和特征向量的意义[19]。一个二维函数与二维高斯核卷积相当于在其每一点的一个尺度为ρ的邻域内加权平均。所以散射矩阵Cρ的特征值的意义是,在尺度为ρ的邻域内,灰度变化最快的方向为v1,且变化率为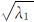 ;而在同一点的同一邻域内,变化最慢的方向为v2,且变化率为
;而在同一点的同一邻域内,变化最慢的方向为v2,且变化率为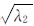 。以下分3种情况来讨论图像的局部特征。
。以下分3种情况来讨论图像的局部特征。
(1) λ1≈λ2≈0。图像在该点附近沿任何方向的灰度变化都很小,即对应于图像的平坦区。
(2) λ1»λ2≈0。图像沿某一方向的变化率远大于沿垂直于此方向的变化率。这时,图像具有明显的边缘或流线状结构。即在这一局部的灰度值表现出很强的相干性。定义
T=(λ1-λ2)2=(c11-c22)2+4c122
为图像局部相干性的量度。显然,平坦区的相干性为T≈0,边缘区的相干性很大。
(3) λ1≈λ2»0。图像在两个相互垂直的方向上灰度变化都很快。即图像存在拐角或T形局部结构。这时,图像的相干性也很小,T≈0。
所以,在构建模型时,将散射矩阵引入核函数,即自适应核中的梯度协方差矩阵修正为散射矩阵。
4 基于核回归的SAR图像自适应相干斑抑制方法通过对SAR图像点目标和散射矩阵特征的分析,为了在抑制相干斑的同时,获得更丰富的图像细节信息,能更好地区分出目标点与背景,笔者将图像幅度值和散射矩阵引入核函数中,进而给出本文的主要方法--基于核回归的SAR图像自适应相干斑抑制方法。
4.1 平滑参数的改进在核回归方法中,平滑参数h是控制着平滑程度的重要参数,对平滑结果有着至关重要的作用。为此,首先对其进行敏感度分析,以决定如何将图像幅度值引入到核函数中。
对式(3)进一步演算,得到
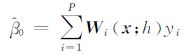
式中
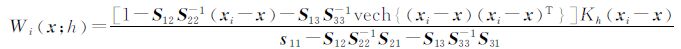
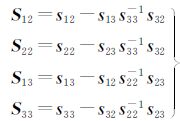
直接计算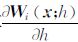 可得到
可得到 ,该方法理论上可行,但由于sij(i,j=1,2,3)中都包含h,其复杂度可见一斑。为了降低计算的复杂度,笔者采用数值模拟,得到敏感度的曲线直观图,发现其整体变化趋势。
,该方法理论上可行,但由于sij(i,j=1,2,3)中都包含h,其复杂度可见一斑。为了降低计算的复杂度,笔者采用数值模拟,得到敏感度的曲线直观图,发现其整体变化趋势。
图 2给出了光滑参数h的敏感性示意图,从图中可以看出,当h小于10时,每个数据点对应的核值变化比较剧烈,随着h的增大,核函数取值变化幅度下降,且估计值对h变化越来越不敏感。
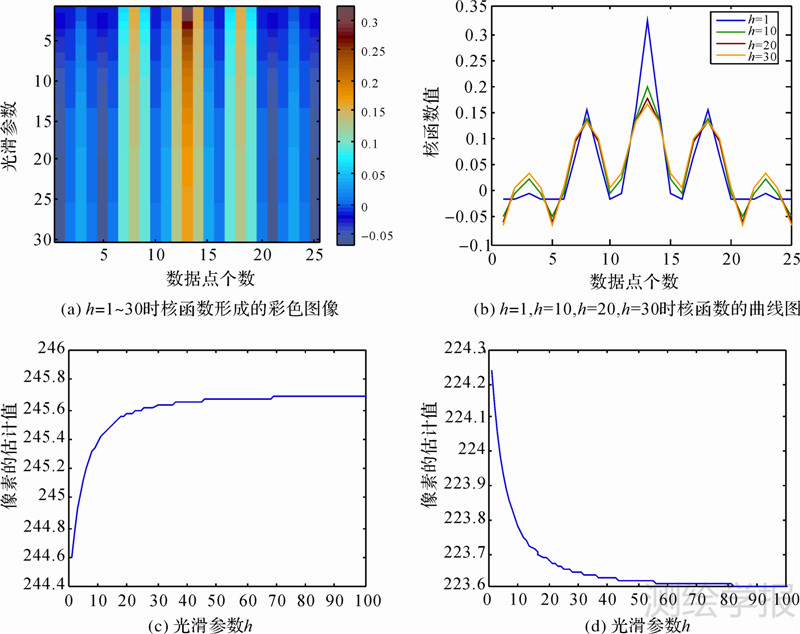
|
| 图 2 P=25时核函数随h的敏感性示意图 Fig. 2 The sensitivity analysis on kernel function with h when P=25 |
因此,在对平滑参数h的改进时,对背景区域,设计其参数取值在敏感范围之外;而对目标区域,为了减少背景对目标的影响,设计其参数取值在敏感范围之内。
对平滑参数h进行加权,即
选取μ1(yi)=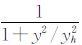 ,yh是目标与背景分界点处的灰度值,ρ是控制图像幅度值对平滑参数的衰减率。式(6)的含义是在图像幅度值小的地方(对应图像的背景区域)多平滑,而在图像幅度值大的地方(对应图像的目标区域)则少平滑。因此,这种平滑最终的作用是抑制背景区域噪声,而目标点的幅值基本不变。
,yh是目标与背景分界点处的灰度值,ρ是控制图像幅度值对平滑参数的衰减率。式(6)的含义是在图像幅度值小的地方(对应图像的背景区域)多平滑,而在图像幅度值大的地方(对应图像的目标区域)则少平滑。因此,这种平滑最终的作用是抑制背景区域噪声,而目标点的幅值基本不变。
按从小到大的顺序将图像的幅度重新排列,记为v。假定目标点在图像中所占的比例为r,记i0=[N(1-r)-0.5],其中N为图像的像素点总数,[·]表示取整。则yh的取值应为[19]为
试验验证,ρ的取值一般在6~10之间,否则衰减太慢或太快都影响处理效果。
4.2 控制核的改进 4.2.1 扩散张量的设计
考虑扩散张量D=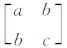 ,它是一个正定对称矩阵,用以调整梯度协方差矩阵以得到更丰富的图像局部信息。记
,它是一个正定对称矩阵,用以调整梯度协方差矩阵以得到更丰富的图像局部信息。记
记w1、w2为D的特征值(w1>w2),v1、v2是与之对应的特征向量。则有v2=[-sinθ cosθ],且
从而设计扩散张量D的问题等价于设计特征值w1,w2和方向角θ的问题。
根据矩阵特征分解定理,则D= wiviviT,且▽f=∂f/∂v1v1+∂f/∂v2v2,则
wiviviT,且▽f=∂f/∂v1v1+∂f/∂v2v2,则
相比于梯度向量,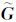 在灰度下降的不同方向给予了不同的权重。
在灰度下降的不同方向给予了不同的权重。
如果将扩散张量的特征向量确定为散射矩阵Cρ的两个特征向量v1、v2,这样θ也就确定了。即设计扩散张量D的问题进一步简化为设计特征值w1,w2的问题。
利用式(10),可以分别独立地控制在v1、v2方向的系数。这就从机制上保证了基于扩散张量的自适应核回归方法有更优的性能。根据图像滤波的要求不同,下面给出两种设计w1、w2的具体方法。
4.2.1.1 边缘增强张量扩散当ρ=0时,散布矩阵为J0,它只有一个非零特征值λ1=▽f2,且对应的特征向量为v1=▽f/|▽f|=η。另一特征向量为v2=ξ(即图像水平集的单位切矢量)。设计w1、w2为
式中,函数g(·)可选用任何一种边缘函数(如g(λ1)=1/[1+(λ1/K)2])。可以看出,沿η方向的滤波随梯度模而变化,沿ξ方向总是以μ2=1进行。它克服了对靠近“边缘”的噪声不能有效清除的缺点。
4.2.1.2 相干增强张量扩散对图像的转角或T形结构而言,上述边缘增强张量扩散方法不能有效的保护其结构。相干性测度Hc不仅能检测边缘(Hc»0),也能检测转角或T形结构(Hc≈0),所以利用它来构造张量扩散矩阵就有可能同时保护边缘和转角或T形等局部结构。为此,利用ρ>0的散射矩阵Cρ来提取相干性Hc,然后令D的特征值为
式中,α为一很小的数(如α=0.001)。沿Cρ的主方向v1(即图像变化最快的方向),扩散率保持为一个很小的正常数,从而保护边缘。另一方面,沿v2方向(即图像变化最慢的方向),根据相干性的强弱自动调节扩散率μ2,当(λ1-λ2)2很大时,指数exp[-1/λ1-λ22]接近于1,从而使w2≈1。当图像的局部没有显著的相干性时,这可能是图像有转角或T形结构等地方。按照式(12),w2≈α,即沿v2方向的扩散也将十分缓慢。这样就保护了“转角”、T形等局部结构不被模糊化。
4.2.2 模型建立考虑控制核矩阵为
式中
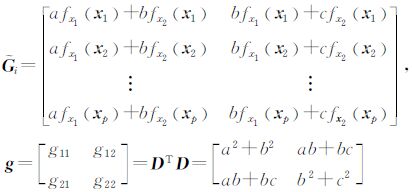
对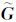 i做奇异值分解
i做奇异值分解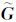 i=UiSiViT,其中,Si是2×2对角矩阵,表示主方向上的能量(
i=UiSiViT,其中,Si是2×2对角矩阵,表示主方向上的能量(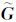 i的主方向为其最小(非零)奇异值对应的奇异向量[20])。正交2×2矩阵Vi的第2列v2=[υ1 υ2]定义了主方向角度θi
i的主方向为其最小(非零)奇异值对应的奇异向量[20])。正交2×2矩阵Vi的第2列v2=[υ1 υ2]定义了主方向角度θi
从形式上看,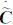 i中g的元素是不随i的变化而变化,但在g的构造中(其特征向量、特征值均是由Cρ确定),它的元素也是随着i的变化而变化。
i中g的元素是不随i的变化而变化,但在g的构造中(其特征向量、特征值均是由Cρ确定),它的元素也是随着i的变化而变化。
由于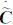 i可能是秩亏或不稳定的,因此在这种情况下不能直接求矩阵的逆,需要利用对角化或正则方法获得比较稳建的估计。将
i可能是秩亏或不稳定的,因此在这种情况下不能直接求矩阵的逆,需要利用对角化或正则方法获得比较稳建的估计。将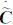 i分解为3个部分[5, 10]
i分解为3个部分[5, 10]
式中,Uθi=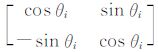 是旋转矩阵;Λi=
是旋转矩阵;Λi=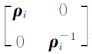 是伸缩矩阵;γi,θi,ρi分别是尺度、旋转和伸缩参数。
是伸缩矩阵;γi,θi,ρi分别是尺度、旋转和伸缩参数。
根据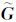 i的主方向的能量计算伸缩参数ρi为
i的主方向的能量计算伸缩参数ρi为
式中,λ′是正则参数,使分母不会为0。定义尺度参数γi为
式中,λ″也是正则参数,使γi不会为0,M是局部分析窗中的样本数。
5 数值实现与试验验证利用改进的平滑参数和控制核建立新的核函数,从而形成基于核回归的SAR图像自适应相干斑抑制方法。
基于此,建立最优化模型为
式中,Him=hi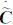 i-1/2,hi和
i-1/2,hi和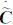 i的意义与式(6)、式(13)中意义相同。
i的意义与式(6)、式(13)中意义相同。
首先给出方法的实现步骤,然后对实测SAR图像进行相干斑抑制,并与增强Lee滤波方法[12]、增强Frost滤波方法[13]、经典核回归方法[6]、自适应核回归方法[7]、PM扩散方法[14]进行比较,验证方法的有效性。
5.1 实现步骤为了实现基于核回归的SAR图像自适应相干斑抑制方法,笔者将方法的实现步骤总结如下。
步骤1:确定初始参数P、h,逐点得到经典核回归方法估计结果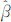 0、
0、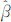 1。
1。
步骤2:根据图像梯度向量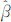 1,给定高斯核参数ρ,确定计算每一像素点的散射矩阵Ĉρ,并求其特征值λ1、λ2及特征向量v1、v2,得到角度θ。
1,给定高斯核参数ρ,确定计算每一像素点的散射矩阵Ĉρ,并求其特征值λ1、λ2及特征向量v1、v2,得到角度θ。
步骤3:根据图像处理目的,利用取值公式(11)或(12) 得到w1、w2,进而根据式(9)得到扩散张量的元素a、b、c。
步骤4:计算局部梯度矩阵Ĝi,求其奇异值s1、s2及奇异向量υ1、υ2,利用式(16)和式(17)得到图像的尺度、旋转和伸缩参数估计γi、θi、ρi。
步骤5:通过步骤4估计的γi、θi、ρi,利用式(15)得到高斯核的协方差矩阵估计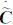 i。
i。
步骤6:利用式(6)对平滑参数进行修正,同时Him=hi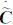 i1/2,进而得到自适应核KHim(xi-x),相应地得到权矩阵WX=diag{KH1m(x1-x),KH2m(x2-x),…,KHpm(xP-x)};
i1/2,进而得到自适应核KHim(xi-x),相应地得到权矩阵WX=diag{KH1m(x1-x),KH2m(x2-x),…,KHpm(xP-x)};
步骤7:利用式(3)得到像素点的估计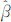 0,逐点估计像素,得到去噪后的图像。
0,逐点估计像素,得到去噪后的图像。
对一幅实测SAR图像(图 3(a))进行相干斑抑制。其中图 3(a)的滤波效果见图 3(b)~(g)。其中图 3(b)为增强Lee滤波方法处理后的图像,窗口尺寸为7;图 3(c)为增强Frost滤波方法处理后的图像,窗口尺寸为7;图 3(d)为经典核回归方法处理后的图像,窗口尺寸为17,初始平滑参数为10;图 3(e)为自适应核回归方法处理后的图像,其中参数λ′=0.1,λ″=0.001,α=0.01;图 3(f)为PM扩散方法处理后的图像;图 3(g)为本文提出的方法处理后的图像(利用式(12)),其中参数λ′、λ″、α与图 3(e)处理时取值相同。

|
| 图 3 SAR图像以及相干斑处理效果图像 Fig. 3 The SAR image and its resultant image by different methods |
图 3中的结果显示,增强Lee滤波方法处理后的图像中仍然包含较多噪声点,点目标也存在一定程度的模糊。 增强Frost滤波方法滤波以后图像中的点目标明显被模糊了。经典核回归方法滤波后的图像的目标点被模糊程度较增强Lee滤波和增强Frost滤波更严重。自适应核回归方法滤波后的图像强化了边缘,但点目标被模糊的程度强于经典核回归方法。PM扩散方法能比较好地同时保护了点目标和边缘目标,处理效果比较理想。本文提出的方法能充分起到保护点目标的作用,图中的红色圆圈内的点目标清晰可见,同时绿色框内的边缘目标体现地也比较好。
采用等效视数和目标杂波比对各种方法处理效果进行比较。等效视数是评价相干斑抑制效果的主要指标[21]
ENL=μ2/δ2
式中,μ为图像均匀区域的像素强度的均值;δ为相应区域的标准差。等效视数越大,说明相干斑抑制效果越好,反之越差。目标杂波比[21](target clutter ratio,TCR)是定量度量图像目标和背景杂波对比度、背景抑制的指标,它定义为图像中目标区域内幅度最强的像素幅度与其周围杂波强度之比,具体如下
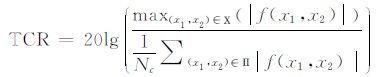
式中,Ⅱ为杂波区域;Χ为目标区域;NC为杂波区域的像素数。目标杂波比的值越大,则表明目标对背景杂波的对比度越强、背景抑制越充分。
各种方法的等效视数与目标杂波比见表 1。从表 1中可以看出,文中提出的方法在抑制噪声和保护目标方面的优势。
| 评价标准 | ||
| 等效视数 | 目标杂波比 | |
| 原图 | 26.139 0 | 14.356 9 |
| 增强Lee滤波 | 105.535 4 | 8.285 3 |
| 增强Frost滤波 | 105.650 3 | 7.331 8 |
| 经典核回归 | 69.916 6 | 4.448 1 |
| 自适应核回归 | 283.859 4 | 1.959 3 |
| PM扩散 | 291.033 1 | 12.636 4 |
| 本文的方法 | 300.488 5 | 13.294 3 |
本文针对SAR图像的相干斑抑制问题,在经典核回归方法的基础上,从平滑参数和控制核两个角度入手,提出了基于核回归的SAR图像自适应相干斑抑制方法,采用幅度信息和散布矩阵来修正核函数来达到抑制相干斑的同时保护点目标的效果。该方法具有以下特点:
(1) 核回归作为一种非参数估计方法,在图像处理领域中,有较强的理论和应用价值,尤其在SAR图像相干斑抑制中还未见相关文献涉及。本文结合SAR图像的幅度分布特性,提出了基于核回归的SAR图像自适应相干斑抑制方法。
(2) SAR图像幅度分布特性指导了相干斑抑制方法的改进方向,在相干斑抑制的基础上,充分保护了点目标。
(3) 为了更好地利用图像局部信息,提出了基于散射矩阵的核修正方法,在抑制噪声的同时能更好地保持边缘细节。其中,方法的关键技术是扩散张量的特征值的选取方案,根据不同的图像处理目的,可以设计不同的特征值构造方法。其方案选取的灵活性也是该方法的一个主要优点,能适用于不同的图像处理应用中。
(4) 由于本文涉及的参数比较多,方法的自适应性需要进一步研究。同时鉴于方法的完善性,将进一步研究该方法的统计性质。
| [1] | CHRIS O, SHAUN Q. Understanding Synthetic Aperture Radar Images[M]. Beijing: Publishing House of Electronics Industry,2009. |
| [2] | IAN G, FRANK H. Digital Processing of Synthetic Aperture Radar Data: Algorithm and Implementation[M]. Boston: Artech House, 2007. |
| [3] | QIU P. The Local Piecewisely Linear Kernel Smoothing Procedure for Fitting Jump Regression Surfaces[J]. Techno Metrics, 2004, 46: 87-99. |
| [4] | XU Yong, ZHANG Dapeng. Kernel Method and Its Application for Model Classification[M]. Beijing: National Industry Press, 2010.(徐勇,张大鹏,杨健.模式识别中的核方法及其应用[M].北京:国防工业出版社,2010.) |
| [5] | EUBANK R. Nonparametric Regression and Spline Smoothing[M]. New York: Marcel Dekker, 1999, 157. |
| [6] | HIROYUKI T,SINA F, PEYMAN M. Kernel Regression for Image Processing and Reconstruction[J]. IEEE Transactions on Image Processing, 2007, 16 (2):349-366. |
| [7] | HIROYUKI T. Locally Adaptive Kernel Regression Methods for Multi-dimensional Signal Processing[D]. California: UC Santa Cruz, 2010. |
| [8] | ELAD M, HEL Y. A Fast Super-resolution Reconstruction Algorithm for Pure Translational Motion and Common Space-invariant Blur[J]. IEEE Transactions on Image Processing, 2001, 10(8):1187-1193. |
| [9] | ELAD M. On the Origin of the Bilateral Filter and Ways to Improve It[J]. IEEE Transactions on Image Processing, 2002, 11(10): 1141-1150. |
| [10] | FARSIV S, ROBINSON D, ELAD M. Robust Shift-and-add Approach to Super-resolution [C]//Proceedings of the SPIE Annual Meeting.San Diego: [s. n.], 2003. |
| [11] | WAN Qing. The Kernel Regression Image Denoise Method Based on Nonparameter Estimation[D]. Wuhan: South Central University for Nationalities,2008.(万青.基于非参数估计的核回归图像去噪[D].武汉:中南民族大学,2008.) |
| [12] | LEE S J. Digital Image Enhancement and Noise Filtering by Use of Local Statistics [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1980,2(2):165-168. |
| [13] | FROST V S, STILES J A, SHANMUGAN K S, et al, A Model for Radar Images and Its Application to Adaptive Digital Filtering of Multiplicative Noise[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1982, 4(2): 157-166. |
| [14] | PERONA P, MALIK J. Scale Space and Edge Detection Using Anisotropic Diffusion [J]. IEEE PAMI, 1990,12: 629-639. |
| [15] | GIUSTO D D. SAR Image Filtering Using Wavelet Transform[C]// IEEE International Geoscience and Remote Sensing Symposium Proceedings.Washington: IEEE Publications, 1995: 2153-2155. |
| [16] | ZHANG Jun, LIU Jian. A Speckle Reduction Algorithm by Soft-thresholding Based on Wavelet Filters for SAR Images [J]. Acta Geodaetica et Cartographica Sinica, 1998, 27 (2):119-124. (张俊, 柳健. SAR图像斑点噪声的小波软门限滤除算法[J]. 测绘学报, 1998,27 (2): 119-124.) |
| [17] | HUANG Shiqi, LIU Daizhi. Research on Method and Application of Speckle Noise Reduction of SAR Image[J].Acta Geodaetica et Cartographica Sinica, 2006,35 (3): 245-249.(黄世奇,刘代志. SAR图像斑点噪声抑制方法与应用研究[J]. 测绘学报,2006,35 (3): 245-249.) |
| [18] | XIE Meihua, WANG Zhengming. Nonlinear Diffusion Equation for Image Denoising Based on SAR Amplitude and Gradient Information[J].Journal of Astronautics,2006, 27(2): 233-237(谢美华,王正明.基于幅度与梯度综合信息的SAR图像非线性扩散去噪方法 [J].宇航学报,2006,27(2):233-237.) |
| [19] | WEICKERT J. Application of Nonlinear Diffusion in Image Processing and Computer Vision[J]. Acta Mathematica Universitatis.Comenianae, 2001, LXX(1):33-50. |
| [20] | FENG X, MILIANFA P. Multiscale Principal Components Analysis for Image Local Orientation Estimation[C]//The 36th Asilomar Conference Signals, Systems and Computers.Pacific Grove:[s.n.],2002:478-482. |
| [21] | WEI Zhongquan. Synthetic Aperture Radar Satellite [M]. Beijing: Science Press, 2001 (魏钟铨, 合成孔径雷达卫星 [M], 北京: 科学出版社, 2001) |