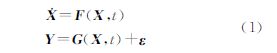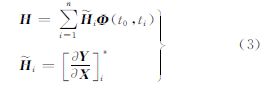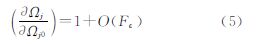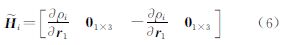2. 中国科学院 上海天文台,上海 200030;
3. 61363部队,陕西 西安710054
2.Shanghai Astronomical Observatory,the Chinese Academy of Sciences,Shanghai 200030,China;
3. 61363 Troops,Xi’an 710054,China
1 引 言
目前卫星星座的主流是单中心天体下的受摄二体轨道[1]。利用星间测距测速的多星联合定轨能够自治地提供星座自身的导航,最大限度地降低多传感器、多数据源带来的系统复杂性,因此成为GPS等导航系统的星座自主定轨的首选技术手段[2]。但是,传统星座的整体旋转一直是 SST 自主定轨的一个技术上的难题。单纯利用星间距离及其变化能够完全确定星座中各卫星的大小、形状和轨道面内运动,以及星座的相对定向,但是对星座绝对定向参数的变化不敏感[3, 4]。目前常用的改进方法主要用来解决秩亏问题,最为简便有效的方法是充分利用卫星的先验轨道信息(如固定轨道的升交点赤经)以消除秩亏[5],其不足是随着系统误差的累积,导航精度有一定的时效限制。为此也有人提出利用地面锚固点的单点定位方法定期消除星座整体旋转的误差累积[6, 7, 8, 9],但是如此一来,在一定程度上降低了系统的自主性。另一种方法是利用星载光学传感器(如星敏感器)获取至其他卫星的视向方向,从而实现星座的绝对定向[6, 10]。研究表明,该方法的测角观测量不如距离观测量的几何强度,并且增加了系统的复杂性。
限制性三体问题下的平动点轨道因其独特的动力学特性使其具备潜在的工程应用背景。目前国际上的平动点飞行任务计划有上升趋势,我国的嫦娥二号也已在月球探测任务结束后进入了日地系L2平动点轨道。但是利用平动点轨道的导航研究尚不多见,早在2002年,文献[11]就建议利用SST自主导航以缓解深空网的测控任务压力;文献[12, 13]提出名为“Liaison Navigation”的自主导航系统方案,用于支持月球南极探测并最终实现月球全球10 m精度的导航[12]。
引进圆型限制性三体问题(以下采用CRTBP)下的平动点轨道,将是解决传统星座SST自主定轨绝对定向的一种有效途径。在地-月-飞行器组成的CRTBP中,飞行器的空间轨道可以拓展到以地球为中心、半径超过40万km的地月大尺度空间。受地月两大天体的共同影响,地月连线的某些特殊位置(即共线平动点)附近区域,引力场表现出强非对称性[12, 13, 14, 15],使得CRTBP模型下的一类简单对称轨道类型——Halo轨道族在平动点附近特定空间具有独特的分布单值性,这一点是二体问题轨道所不具备的。因此,利用Halo轨道与二体问题轨道组成扩展星座,在SST获得扩展星座的大小形状和相对定向信息的同时,还能够唯一确定Halo轨道的绝对位置信息,从而保证整体星座的空间绝对定向。由于Halo轨道的运动空间范围广,原则上仅需要附加一个Halo轨道飞行器即可实现基于星间链路的星座自主定轨。
本文从系数矩阵的相关性出发,指出引进Halo轨道在改进定轨法矩阵正定性中的积极作用;以LMO-Halo星座为例,分析并数值验证了CRTBP意义下SST星座自主定轨的可行性。
2 CRTBP下Halo轨道的特性 2.1 CRTBP与LL1/LL2 Halo轨道CRTBP是深空探测器轨道力学中常用的一种力学模型,是天体力学中二体问题之外最基本的力学模型之一[16]。它讨论的是质量可以忽略的小质点在两个以圆轨道相互绕转的大质点天体引力作用下的运动情况,是某些天体力学和宇航动力学问题的一种近似。
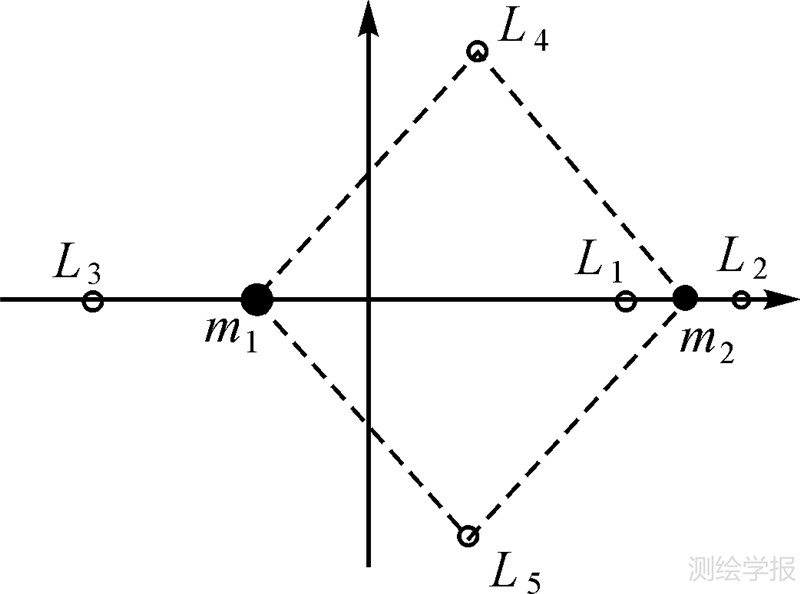
如图 1所示,通常在随两个大天体一起绕转的质心旋转坐标系中研究小质点的运动。此模型下存在5个动平衡点,即平动点L1、…、L5,它们与两个大天体组成不变的空间构形(见图 1)。其中3个共线平动点(即L1、L2、L3点)附近存在着大量的周期和拟周期轨道,特别是应用最为广泛的Halo周期轨道族[16]。图 2展现了地月系质心旋转坐标系中L1和L2点(记为LL1和LL2)附近的某些Halo轨道。
|
| 图 1 CRTBP常用的质心旋转坐标系及5个平动点 Fig. 1 Jacobi coordinate system and the five libration points of CRTBP |
|
| 图 2 地月系L1和L2点附近某些Halo轨道示意图 Fig. 2 Some sample Halo orbits around LL1 and LL2 |
地月空间中,飞行器在CRTBP意义下的轨道受地月两大天体的共同影响,由于受力特点差异其轨道性态显著不同。
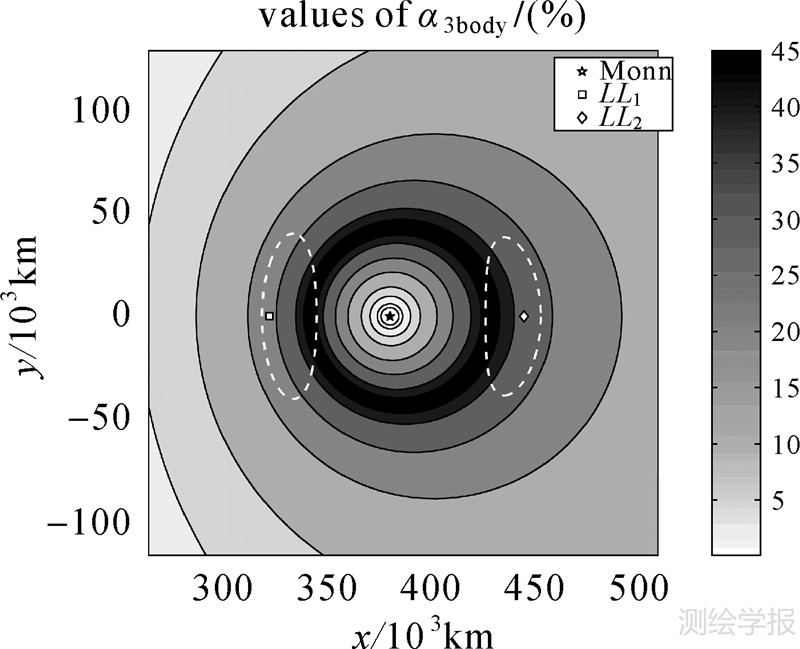
(1) 地球和月球附近的飞行器轨道(如低轨地球卫星LEO和低轨月球卫星LMO)是典型的受摄二体问题轨道。与地球(或月球)中心引力相比,月球(或地球)第三体引力摄动的影响因素十分微弱,量级分别约为10-3和10-4以下,因此,引力场关于单中心天体具有近似球对称性,轨道本质为单中心天体引力作用为主的稳定轨道,基本性态表现为空间分布上的近似各向同性。这一点由图 3可以看出,图中给出了地球的第三体引力摄动所占合力的百分比分布,图中心的月球附近区域的引力场表现出:① 月球中心引力占主导地位;② 空间球对称性强。
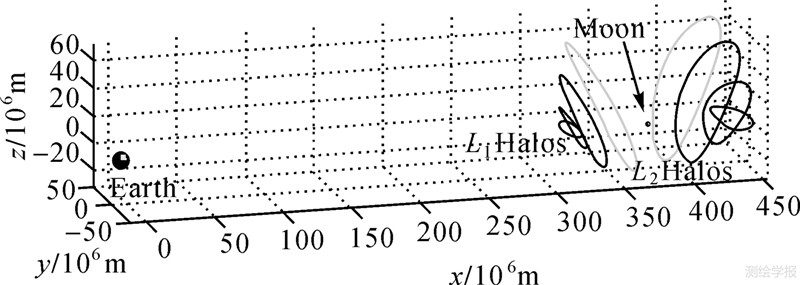
(2) 地月连线上距离月心6~7万km远的LL1和LL2平动点附近(如图 3的两处虚线标注区域),除了位置特殊外更有丰富动力学信息和轨道性态。在地月两大天体引力的共同作用下,共线平动点附近的引力场除了关于白道XY平面的镜面对称外,表现出强非对称性。① 共线平动点轨道本质上是不稳定的;② 就Halo轨道运动的局部空间细节来看,引力场变化较为明显,表明这类特殊的条件周期轨道的自身存在就已具有某种程度上的空间绝对定位定向信息。事实上,作为简单对称的周期轨道类型,Halo轨道要求满足关于XZ平面对称(如图 4所示),因此其三维轨道相对于XZ平面为正交穿刺,即穿刺点在质心旋转坐标系下的状态量为[x0 0 z0 0 ý0 0]T,表明只有在特定区域并且满足一定的初始条件,才会存在周期轨道。这些特点都是受摄二体问题轨道所不具备的,也正是其能够介入传统星座改善绝对定向的动力学依据。
|
| 图 4 地-月系L2点附近的一条Halo轨道(质心旋转坐标系) Fig. 4 One Halo orbit around L2 point in the Earth-Moon system |
以两星星座为例,在月心惯性系下运动微分方程和测量方程可表示为
分别对运动方程和观测方程进行线性化,得到关于初始状态改正数向量x0的线性化误差方程
式中,Y和y分别为观测向量及其残差向量;ε是测量噪声;且有扩展系数矩阵
式中,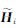 和Φ(t0,ti)分别表示观测方程的系数矩阵和状态转移矩阵。
和Φ(t0,ti)分别表示观测方程的系数矩阵和状态转移矩阵。
若要满足参数估计的法矩阵正定,要求扩展系数矩阵H的各列之间无线性或复共线性关系。
3.1 受摄二体问题星座在传统受摄二体问题中,轨道状态量可采用轨道根数σ=[a e i Ω w M]T或位置速度向量[r v]表示。若采用轨道根数形式,有
XT=[σ1Tσ2T]
对于星间测距观测量ρi=|r1-r2|,有
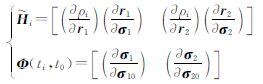
对升交点赤经Ω计算偏导数,已知ΔΩ的旋转轴方向为k=[0 0 1]T,有
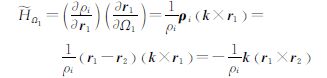
同理可得
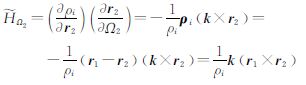
因此,有
另一方面,由根数摄动公式[16],有Ωj(j=1,2)的状态转移关系
式中,一阶小量通常与中心天体的扁率摄动量级相当。将式(4)和式(5)代入式(3),则扩展系数矩阵H中与Ωjj=1,2对应的两列之间有显著的复共线性关系,SST星座自主定轨有秩亏问题(严格的说是严重的病态性),表现为星座整体旋转[3, 18]。
3.2 LMO-Halo星座与(受摄)二体问题轨道相不同,CRTBP模型下的Halo轨道无法用轨道根数表达,只能用位置和速度向量表示轨道状态
XT=[r1Tv1Tr2Tv2T]
基于星间测距观测量的偏导数矩阵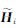 具有线性相关性[17],因为
具有线性相关性[17],因为
因此,若要满足参数估计的法矩阵正定,要求两飞行器的状态转移矩阵Φ(ti,t0)应具有足够的差异性,从而去除或减弱扩展系数矩阵H的线性或复共线性。
由状态转移矩阵的变分方程
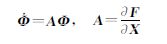
可知,状态转移矩阵可表示为
Φ=Φ0eA(t-t0)
显然,状态转移矩阵的特性完全由变分方程系数矩阵A的特征值决定,而矩阵A是力F对状态的偏导数,因此仍是与力学特性紧密相关的。
前面已对两类轨道的力学特性差异进行了对比分析,它既导致了两类轨道性态的差异,同样也导致了状态转移矩阵Φ(ti,t0)的差异。这种差异有可能打破传统二体轨道星座的系统相关性,加强定轨法矩阵的正定性,从而保证星座全部轨道状态参量的唯一确定性。
由于Halo轨道仅在质心旋转坐标系下表现出其条件周期特征,且其精确数值轨道必须在坐标系下进行构造,因此难以给出传统月心惯性系下的一般性解析分析结果,下面给出数值仿真予以验证。
4 定轨仿真验证及分析为验证平动点轨道对传统星座SST自主定轨的贡献,在地月系CRTBP模型下构造LMO-Halo星座并进行SST测定轨仿真。其中,Halo轨道的构造方法是先采用Richardson三阶解析解确定轨道初值,然后用微分改正算法精化轨道[19, 20, 21]。
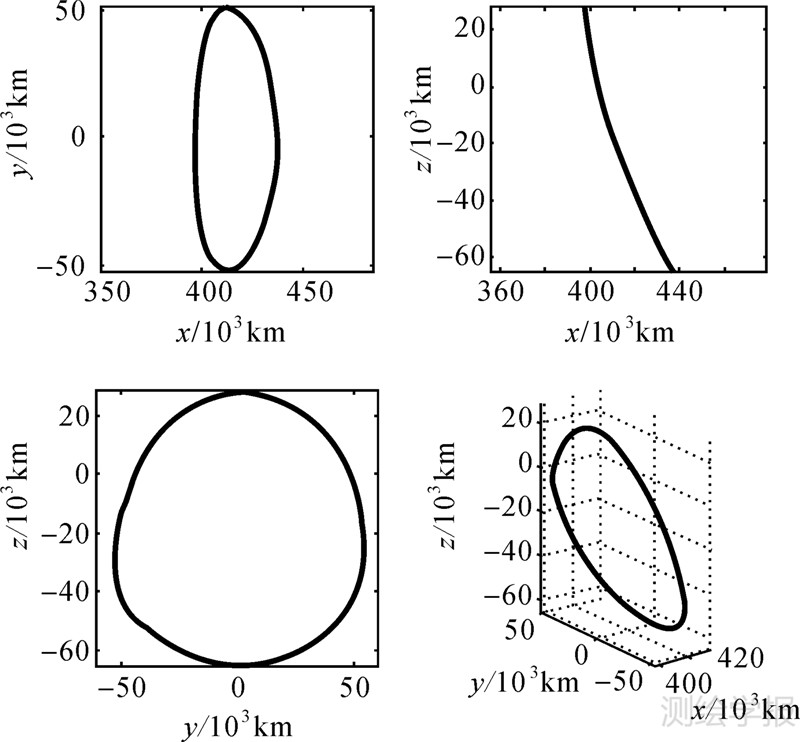
为反映不同性态的Halo轨道对定轨的影响,在地月系L1点附近的Halo轨道族内相隔较远选取了2条Halo轨道,图 5给出了质心旋转坐标系下相对月球的轨道构型,其中Halo1轨道的稳定性优于Halo2,轨道周期分别约为10 d和15 d。
|
| 图 5 地-月系L1点的两条Halo轨道(质心旋转坐标系) Fig. 5 Two Halo orbits around L1 point in the Earth-Moon system |
需要说明的是,Halo的数值轨道首先在CRTBP模型下构造,进而转换至月心惯性系进行定轨。这里的月心惯性系定义为:XY平面为白道面,且令X轴与仿真初始时刻的地月连线一致,以体现Halo轨道特征。
LMO为100 km高的月球圆极轨卫星,3个飞行器的初轨状态见表 1。
| X/ km | Y/ km | Z/ km | Vx/ (km/s) | Vy/ (km/s) | Vz/ (km/s) | |
| LMO | -1 838.0 | 0 | 0 | 0 | 0 | 1.63 |
| Halo1 | -22 652.2 | 0 | -112 498.6 | 0 | 0.023 45 | 0 |
| Halo2 | -63 253.7 | 0 | -12 411.4 | 0 | -0.023 00 | 0 |
| *注:见文中定义 | ||||||
其他仿真条件为:观测弧长以Halo轨道周期T为单位,分别取0.5 T、0.75 T和1 T;星间测距观测量采样率60 s,噪声3 m,系统偏差10 m;LMO初轨偏差的位置和速度为100 m和5 mm/s,Halo取500 m和5 cm/s并随机生成;LMO和Halo先验轨道约束分别为3 km和5 km位置、0.3 m/s和5 m/s速度约束;批处理估计LMO和Halo轨道的初始状态参量和全弧段的测距偏差b。
4.1 仿真方案首先分别组成LMO-Halo1和LMO-Halo2两星星座,设计定轨仿真方案如下:
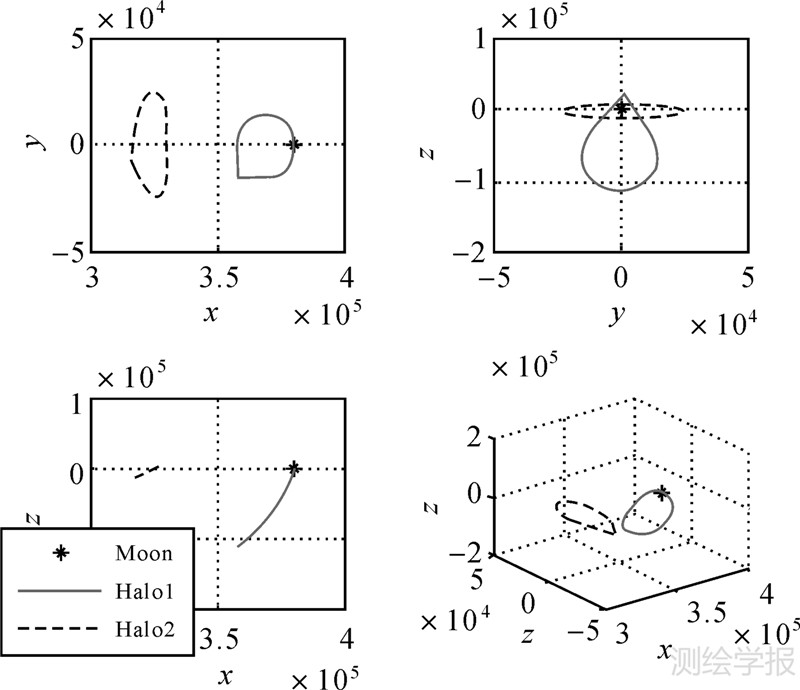
方案1:观测弧长内,星间通视即为有观测数据。由于Halo轨道的空间构型大,对LMO的覆盖性达到甚至超过60%,月球遮挡时段较短且均匀分布,图 6给出了第一天的星间通视分布。
|
| 图 6 LMO与两条Halo轨道的通视性 Fig. 6 Visibility between LMO and two Halo orbits |
方案2:考虑到星间链路用于测轨数据的时段限制,观测数据设计为方案1中每隔1 h取出1 h观测数据,即测轨数据均匀分布,但数据使用率减至方案1的50%左右。
其次,为进一步表明Halo轨道对星座绝对定向的贡献,组合两条星间链路测量数据进行联合定轨。观测弧长取Halo2轨道的0.5 T,解算3个飞行器的初轨和2个测距偏差。
4.2 仿真结果与分析表 2和表 3分别给出了LMO-Halo1、LMO-Halo2的方案1和方案2仿真结果。仅列出了估计参数中位置和测距偏差的误差统计值。
| m |
| 方案 | 定轨弧长 | LMO | Halo1 | b | ||||
| X | Y | Z | X | Y | Z | |||
| 1 | 1T | 0.22 | -0.20 | 0.38 | -3.14 | 14.25 | 0.83 | -0.14 |
| 0.75T | 0.02 | -1.34 | -1.09 | 67.40 | -213.10 | -13.54 | 0.16 | |
| 0.5T | -0.23 | -7.99 | -1.78 | 102.26 | 10.52 | -20.63 | 0.36 | |
| 2 | 1T | 0.14 | 1.51 | -0.65 | 78.31 | -347.66 | -16.37 | -0.93 |
| 0.75T | 0.09 | 64.55 | 1.62 | -49.12 | 545.72 | 11.56 | 1.15 | |
| 0.5T | — | — | — | — | — | — | — | |
| m |
| 方案 | 定轨弧长 | LMO | Halo2 | b | ||||
| X | Y | Z | X | Y | Z | |||
| 1 | 1T | -0.10 | -0.07 | -0.21 | -0.82 | -0.55 | 1.34 | -0.06 |
| 0.75T | 0.08 | 0.07 | 0.08 | 0.97 | 0.61 | -2.27 | 0.13 | |
| 0.5T | -0.21 | -0.30 | 0.14 | 1.03 | 6.19 | 6.27 | 2.72 | |
| 2 | 1T | -0.01 | -0.35 | 0.13 | 1.02 | 14.81 | 25.98 | 6.47 |
| 0.75T | -0.15 | -0.21 | -0.48 | 0.10 | -13.33 | -21.45 | -4.12 | |
| 0.5T | -0.27 | 6.91 | -1.35 | 4.39 | 304.77 | -57.39 | -6.34 | |
定轨仿真的统计结果表明,平动点轨道的介入能够满足SST自主定轨的系统可观性要求。尽管单链路定轨法矩阵的条件数达到1e16以上,但是其谱分解的最小特征值可以保证远离零值。通过增加观测弧长或双链路数据组合,最小特征值迅速增加,从而保证法矩阵的正定性。此外,链路定轨的同时还能够对测距偏差进行自校准标定,这也表明参数估计过程无秩亏问题。
表 2~表 4的结果对比表明:
| m |
| 方案 | X | Y | Z | |
| 1 | LMO | -0.04 | 0.01 | 0.17 |
| Halo1 | -1.13 | 5.27 | 0.08 | |
| Halo2 | -1.15 | 1.05 | 7.93 | |
| b1/b2 | -0.23 | 0.54 | ||
| 2 | LMO | -0.15 | 0.54 | 0.15 |
| Halo1 | -24.51 | 111.54 | 5.14 | |
| Halo2 | -0.53 | 7.42 | 10.48 | |
| b1/b2 | 0.007 | 1.95 |
(1) 传统环月轨道一定的条件下,平动点轨道的选取对两星星座自主定轨精度的影响显著。算例中,LMO的定轨精度可以相差1个数量级,Halo轨道甚至有2个数量级的差异。因此,Halo轨道的优化选取还有待深入分析。
(2) Halo轨道与传统二体轨道的轨道周期差异大,定轨弧长较长。Halo轨道的周期可以接近月球公转周期的一半,需要在定轨弧长上有所平衡。一方面,长弧段使得传统二体问题轨道的初轨误差和力模型误差累积作用显著,影响迭代收敛速度,并且收敛次数对这些误差的量级较为敏感。另一方面,当减小弧长,如由1 T减至0.75 T和0.5 T时,对Halo轨道的数据覆盖下降显著,同样影响定轨精度,甚至迭代不收敛。
(3) 多个平动点轨道介入的联合定轨,能够增强法矩阵的正定性,加快收敛速度,大幅提高星座的整体轨道精度。算例中,双链路定轨的迭代次数在7次左右,而相同条件下的单链路定轨则高达13次。在方案1的条件下,双链路定轨的星座整体轨道精度优于10 m,即使采用方案2也有百米左右的整体定轨精度。
5 结 语引进限制性三体问题下的平动点周期轨道组成扩展星座,能够有效解决传统星座SST自主定轨绝对定向差的困难。结合两种轨道的特点,由SST数据可以获得星座轨道的大小、形状和星座相对定向信息,同时利用Halo轨道在其特定轨道族内的空间分布单值性,可以确定其绝对位置和空间定向,从而保证星座全部轨道状态参量的唯一确定。
平动点轨道的介入,也为常规定轨策略带来了若干新问题,需要进一步的理论探讨和数值验证分析。包括:① 确定平动点周期轨道选取和优化的原则;② Halo轨道的定轨精度评定方法需要做针对性研究;③ 在线处理平动点轨道维持的轨控;④ 复杂力学环境下的星座联合定轨等。
| [1] | YANG Yuanxi. Progress, Contribution and Challenges of Compass/Beidou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1-6. (杨元喜.北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1-6.) |
| [2] | LU Zhenzhu, LI Zhenghang, LIU Wanke, et al. Inspection and Correction of the Revolution Round the Earth of Navigation Satellite Constellation[J]. Journal of Astronautics, 2006, 27(6): 1397-1400. (卢珍珠,李征航,刘万科,等. 导航卫星星座整体旋转的检测与校正[J]. 宇航学报,2006,27(6):1397-1400.) |
| [3] | LIU Yingchun, LIU Lin. Orbit Determination Using Satellite-to-satellite Tracking Data[J]. Chinese Journal of Astronomy and Astrophysics, 2001, 1(3):281-286. |
| [4] | YIM J R, CRASSIDIS J L, JUNKINS J L. Autonomous Orbit Navigation of Two Spacecraft System Using Relative Line of Sight Measurements[C]// Proceedings of the AAS Space Flight Mechanics Meeting. [S.l.]: The American Astronautical Society, 2004. |
| [5] | LI Zhenghang, LU Zhenzhu, LIU Wanke, et al. Method for Eliminating Systematic Error ΔΩ and Δt in Autonomous Orbit Determination of Navigation Satellites[J]. Geomatics and Information Science of Wuhan University, 2007, 32(1): 27-30. (李征航, 卢珍珠, 刘万科, 等. 导航卫星自主定轨中系统误差ΔΩ和Δt的消除方法[J]. 武汉大学学报: 信息科学版. 2007, 32(1): 27-30.) |
| [6] | NIU Fei. Design and Simulation for Satellite Autonomous Integrity Monitoring Based on Inter-satellite-links[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(sup): 73-79. (牛飞. 利用星间链路组合观测量的导航卫星自主完好性监测设计仿真[J]. 测绘学报, 2011, 40(增刊): 73-79.) |
| [7] | CHEN Jinping, JIAO Wenhai, MA Jun, et al. Autonav of Navigation Satellite Constellation Based on Crosslink Range and Orientation Parameters Constraining[J]. Geomatics and Information Science of Wuhan University, 2005, 30(5): 439-443. (陈金平, 焦文海, 马骏, 等. 基于星间测距/轨道定向参数约束的导航卫星自主定轨研究[J]. 武汉大学学报: 信息科学版, 2005, 30(5): 439-443. |
| [8] | ZHU Jun, LIAO Ying, WEN Yuanlan. The Integrated Autonomous Orbit Determination of the Navigation Constellation Based on Crosslink Range and Ground-based Emitter[J]. Journal of National University of Defense Technology, 2009, 31(2): 15-19, 30. (朱俊, 廖瑛, 文援兰. 基于星间测距和地面发射源的导航星座整网自主定轨[J]. 国防科技大学学报, 2009, 31(2): 15-19, 30.) |
| [9] | GENG Tao, LIU Jingnan, ZHAO Qile, et al. Compass Precise Orbit Determination Based on Space-ground Monitoring Network[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(sup): 73-79. (耿涛, 刘经南,赵齐乐, 等. 星地监测网下北斗导航卫星轨道确定[J]. 测绘学报, 2011, 40(增刊): 46-51.) |
| [10] | CAI Zhiwu, HAN Chunhao, CHEN Jinping, et al. Constellation Rotation Error Analysis and Control in Long-term Autonomous Orbit Determination for Navigation Satellites[J]. Journal of Astronautics, 2008, 29(2): 522-528. (蔡志武, 韩春好, 陈金平, 等. 导航卫星长期自主定轨的星座旋转误差分析与控制[J]. 宇航学报, 2008, 29(2): 522-528.) |
| [11] | BECKMAN M. Orbit Determination Issues for Libration Point Orbits[C]//International Conference on Libration Point Orbits and Applications. Girona: NASA, 2002. |
| [12] | HILL K. Autonomous Navigation in Libration Point Orbits[D]. Boulder: University of Colorado, 2007:22-27. |
| [13] | HILL K, BORN G. Autonomous Interplanetary Orbit Determination Using Satellite-to-satellite Tracking[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(3): 679-686. |
| [14] | HICKS K D, WIESEL W E. Autonomous Orbit Determination System for Earth Satellites[J]. Journal of Guidance, Control, and Dynamics, 1992, 15(3): 562-566. |
| [15] | PARKER J S. Low-energy Ballistic Lunar Transfers[D]. Boulder: University of Colorado, 2007. |
| [16] | LIU lin, WANG Xin. An Orbital Dynamics of Lunar Probe[M]. Beijing: National Defense Industry Press, 2006. (刘林,王歆. 月球探测器轨道力学[M]. 北京:国防工业出版社, 2006) |
| [17] | TAPLEY B D, SCHUTZ B E, BORN G H. Statistical Orbit Determination[M]. San Diego: Elsevier Academic Press, 2004. |
| [18] | ZHAO Deyong, PAN Xiaogang, ZHOU Haiyin, et al. Improvement of Satellite-to-satellite Relative Measurement Autonomous Orbit Determination Deficient-rank Based on Combined Orbit Determination Strategy[J]. Journal of Astronautics, 2006, 27(2): 181-186. (赵德勇, 潘晓刚, 周海银, 等. 基于联合定轨策略的星间相对测量自主定轨亏秩问题的改进[J]. 宇航学报, 2006, 27(2): 181-186.) |
| [19] | HOU Xiyun, LIU Lin. The Dynamics and Applications of the Collinear Libration Points in Deep Space Exploration[J]. Journal of Astronautics, 2008, 29(3): 736-747, 771.(侯锡云, 刘林. 共线平动点的动力学特征及其在深空探测中的应用[J]. 宇航学报, 2008, 29(3): 736-747,771. |
| [20] | ZHANG Shouyu, DU Lan. Analyzing the Periodic Orbits Around the Collinear Liberation Points[J]. Science of Surveying and Mapping, 2009, 34(3): 61-63. (张守余, 杜兰. 共线平动点附近周期轨道的分析研究方法[J]. 测绘科学, 2009, 34(3): 61-63.) |
| [21] | WANG Dandan, ZHANG Shouyu, DU Lan, et al. Stability Researching of Halo Families Surrounding Libration Points in Earth-Moon System[J]. Journal of Information Engineering University. 2010,11(4): 508-512. (王丹丹, 张守余, 杜兰, 等. 地月系共线平动点Halo轨道族的运动稳定性研究[J]. 信息工程大学学报, 2010, 11(4): 508-512.) |