立体测量设备使用之前需要进行设备系统参数的标定[1, 2],其中,立体相机是一种常用的立体量测设备,它采用两个或者两个以上的相对几何关系固定的相机以不同视角获取被测目标的影像,并根据交会测量的原理实现三维场景高精度的快速重建[3]。由于立体相机系统中两个相机的内方位元素和相对关系可以事先标定好,当获取了立体影像后,即可以直接进行前方交会,获取绝对的物体三维形状,从而避免了空中三角测量等复杂的摄影测量处理过程,因此具有简便、快速的特点。目前,立体相机已被广泛应用于文物保护、工业测量以及机器人导航等领域[4, 5, 6]。为获取目标点位的精确位置,需要对立体相机进行高精度标定,确定相机的内方位元素(主点、主距以及畸变参数等)以及相机的外方位元素(相机相对于世界坐标系的位置和方位,或者相机间的相对关系)。因此,立体相机的标定是近景摄影测量和计算机视觉领域的一个重要研究课题。
目前常用的立体相机标定方法是重复利用单个相机标定的方法(计算机视觉方法[7, 8, 9]或者摄影测量方法[10, 11, 12]),首先在同一个参考坐标系下对每个相机内外参数分别标定,必要时才利用各自的外参数间接地计算相机间的相对关系。该方法曾被应用于火星探测车[2, 13]、结构光量测系统[1]和模型三维重建[14]等的立体相机的标定过程。这一类方法较为简单、方便,但是标定过程中没有充分利用两相机之间存在的固定的相对关系,因而会影响到标定结果的精度和可靠性。
为了考虑相机间的联系,立体相机标定的另一类方法是将相机之间满足的固定相对关系与相机的成像关系结合起来,直接进行相机参数的解算。文献[15]简单地通过矩阵分解的形式获取相机的焦距以及相对关系,虽然其方法无须迭代计算,可以用于立体相机的标定,但是其标定的精度无法得到保证。文献[16]通过左右相机的核线约束先计算相机的外参数和主距,然后通过最小化一个给定的代价函数计算主点,从而达到立体相机标定的目的。该方法不需已知控制点的坐标,只需要提供一个距离以便计算比例系数,但是不能计算相机的畸变参数,因而其标定精度会受到影响。文献[17—18]等则利用摄影几何的无穷远平面等约束,提出了立体相机标定的线性方法。该方法虽然直接、简单,但是同样也不能计算相机的畸变参数,无法达到非线性方法的精度。文献[19]在立体相机系统安装之前,首先标定内参数,系统安装之后再利用本质矩阵进行立体相机相对关系的标定。该方法虽然兼具较高精度和较好的灵活性,但是内外参数分开标定,并且采用本质矩阵分解形式,因而其过程和精度都还有进一步改进的必要。文献[20]则采用摄影测量中的自检校光束法平差进行立体相机的标定,并且在平差中引入了立体相机的固定基线长度约束,从而在可见光和热红外相机组成的系统标定中获得了较好的标定结果。然而相机之间的固定相对关系除了固定基线长度之外,还表现在固定的相对位置和姿态等6个相互独立的约束上,因而该方法仍然可以通过更全面的约束关系进行改进。
此外,随着人工智能的迅速发展,人工神经网络也被应用到立体相机的标定中[21]。与传统的考虑相机具体模型的方法不同,该方法只通过训练,直接获得立体相机上像点坐标和物方空间点坐标的函数关系,能够满足通常的机器视觉要求。该方法由于不涉及具体的相机模型,能够用于各种类型相机的标定。但该算法容易受到噪声的影响,稳定性有待检验,也无法在空中三角测量中得到应用。
为了充分利用相机间固定的相对关系实现立体相机标定,本文以共线方程为基础,首先推导了立体相机系统中两个相机之间的固定相对关系,然后采用附有条件约束的间接平差模型,将推导出来的固定相对关系约束条件引入自检校光束法平差,实现立体相机系统的标定,在提高稳健性的同时,能够获得较高的相机标定精度。
1 立体相机模型及其固定的相对关系 1.1 立体相机的基本结构本文所研究的立体相机专指两个相机组成的立体相机系统,相机间的相对关系固定。图 1(a)为含有一对立体相机的结构光三维量测设备,固定导杆左右两端各安装一个摄像机,在左右相机之间安装的是一个用于配合立体相机进行量测任务的光栅投影仪。利用该设备进行立体量测任务时,除了需要对左右相机的内参数进行标定之外,还需要对左右相机之间的相对关系进行精密地标定。

|
| 图 1 立体相机的基本结构 Fig. 1 Basic structure of stereo-camera |
图 1(b)为简化的立体相机几何结构图,其中,Cl(Xsl,Ysl,Zsl)和Cr(Xsr,Ysr,Zsr)分别为左右相机的摄影中心在物方空间直角坐标系OXYZ下的坐标;Ol(x0l,y0l)和Or(x0r,y0r)分别为左右两张影像对应的像主点坐标;(X,Y,Z)为物方空间P点在物方空间直角坐标系下的坐标;pl和pr为P点分别在左右影像上的投影,它们在像空间直角坐标系[22]下的坐标分别为pl(xl,yl)和pr(xr,yr)。
右相机相对于左相机的空间关系可用旋转矩阵Rc和平移量[Xc Yc Zc]T来描述(Rc由3个旋转角φc、ωc和κc按照文献[22]或者[23]的方法构造)。假设三维空间中的点P在左右相机的像空间直角坐标系的坐标分别为(Xl,Yl,Zl)和(Xr,Yr,Zr),则左右相机坐标系之间的转换关系表达式为
1.2 相机间的固定相对关系表达式本文采用的相机模型是各参数都具有明确几何意义的共线方程模型。在共线方程模型中,外方位元素指的是相机在世界坐标系中的位置和姿态,通常由外方位线元素和角元素来表示。外方位线元素指的是摄影中心在世界坐标系中的坐标,记为C(Xs,Ys,Zs),而外方位角元素指的是相机在世界坐标中的姿态角,分别记为φ、ω和κ,由这些姿态角构造的旋转矩阵记为R。由姿态角构造的由像空间直角坐标系到世界坐标系的旋转矩阵的方法参考文献[22—23]。
根据式(1)可以进一步得到左右相机外方位元素的关系
式中,下标l和r分别表示的是左右相机,例如Rl和Rr分别表示左相机和右相机相应的姿态角构造的旋转矩阵。 2 引入固定相对关系约束的立体相机系统标定方法 2.1 像点观测值的误差方程采用自检校光束法平差进行相机标定是摄影测量常用的方法[22, 23],为了引入1.2节中所推导的约束条件,采用附有限制条件的间接平差方法[24],其核心是在间接平差中加入强制约束条件,提高平差系统的多余观测数,从而提高相机标定的精度和可靠性。平差观测误差方程是考虑了相机非线性畸变的共线方程。具体见式(4)[22]
式中 Δx和Δy分别表示影像的径向畸变和切向畸变;k1和k2为影像的径向畸变参数;p1和p2为影像的切向畸变参数;a1、a2、a3、b1、b2、b3、c1、c2和c2是旋转矩阵R的元素;x0和y0为像主点坐标;f为主距,影像畸变参数需要在相机标定的过程中同时进行求解。将式(4)按照一阶泰勒级数展开,可以得到线性的间接平差观测误差方程
式中,Vx,y=[vx vy]T为像点观测值[x y]T的残差向量;t=[ΔXs ΔYs ΔZs Δφ Δω Δκ]T为影像外方位元素的改正数;ΔP=[ΔXΔYΔZ]T三维空间点坐标的改正数;Δc=[Δx0Δy0Δf0]T为像主点和主距(线性内参数)的改正数;k=[Δk1Δk2Δp1Δp2]T为相机畸变参数(非线性内参数)的改正数;Ax,y、Bx,y、Cx,y和Dx,y分别为像点坐标[x y]T对外方位元素、空间点三维坐标、相机线性内参数以及非线性内参数的偏导数;Lx,y则为误差方程的常数项。在相机标定中,控制点坐标比较精确,其误差可以忽略,因此,控制点的三维坐标可以视为真值,此时,像点坐标对空间点坐标的偏导数视为零。 2.2 立体相机固定相对关系约束方程本文将式(2)和式(3)所描述几何关系作为强制约束条件加入立体相机标定的平差系统中。假设利用立体相机获取了n对立体影像,对于第i对影像和第j对影像都存在式(3)和式(4)所描述的几何约束关系,对于这两组几何约束关系,利用Rc的正交性从中消去Xc、Yc、Zc和Rc,则可以得到如下的两组约束关系
式中,下标i和j表示的分别是第i和第j个像对,Cl=[XslYslZsl]T和Cr=[XsrYsrZsr]T分别表示左右相机的外方位线元素。由旋转矩阵的正交性可知,式(6)中的9个方程只有3个是相互独立的,因此本文取3×3旋转矩阵对角线元素下方的3个独立元素所决定的3个方程和式(7)表达的3个方程共同作为立体相机标定的约束条件方程,并将它们记为
式中,数字表示行列号,例如式中第1行的21表示式(6)左边矩阵的第2行第1列。式(8)只包括与两个立体像对相关联的4张影像的外方位元素,按照一阶泰勒级数展开得到的线性化形式记为
式中,til、tir、tjl和tjr为影像外方位元素的改正数;Hil、Hir、Hjl和Hjr为Fij对影像外方位元素的偏导数;Fij0为将各个相关的外方位元素初值代入Fij所得到的常数项。在立体相机标定过程中,如果有n个立体像对,则需要选取其中n-1个形如式(8)或者式(9)的相互独立的约束方程作为标定系统的约束条件。例如可以取像对1和2、像对2和3、···、像对n-1和n作为平差的约束条件方程。
2.3 相机标定的参数及其后验方差估计根据2.1节的式(5)和2.2节的式(9),可以将本文的立体相机标定方法总结为如下的优化模型
式中,V为误差方程的残差向量;ΔX为式(5)所有未知数改正数构成的向量;A为对应的误差方程的系数矩阵;L为误差方程的常数项系数;H和T分别为条件约束方程的系数矩阵和常数项向量;P为像点观测值的权矩阵。该模型为附有限制条件的间接平差模型。采用最小二乘法[24]求解该模型,可以得到如下的参数估计表达式
式中,N=ATPA,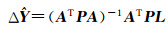 。
。
在对未知数进行估计以后,可以计算出各个观测值的残差,并通过式(12)计算出单位权中误差[24]
式中,n为观测方程的个数;u为未知参数的个数;s为约束条件的个数。这里不直接求解两个相机之间的相对关系参数,但是两个相机之间的相对关系可以通过式(2)和(3)获取,其具体表达式如式(13)所示。
由于立体相机标定模型是非线性模型,因而需要在给定初值的条件下,利用式(11)计算各个未知参数的改正量,并将改正之后的各个参数当作初值,然后重新计算各个参数的改正量,迭代计算,直到各个参数改正量均很小或者单位权中误差无变化为止。另外,为了进一步提高相机标定的稳健性,还利用单位权中误差以及观测值的残差采用选权迭代法进行迭代求解,即通过经验权函数在每一次的迭代中更新观测值的权值[25]
3 试验结果与分析采用平面标定场分别进行了模拟数据和实际数据两组试验。为表述方便,简称本文方法(即引入相机固定相对关系的立体相机标定方法)为方法Ⅰ,而简称常规的标定方法(即通过自检校光束法平差分别对左右相机实现立体相机标定的方法[10])为方法Ⅱ。由于方法Ⅰ在相机标定中强制约束左右相机的固定相对关系,因而最终从不同的立体像对计算的固定相对关系参数都一样。而对于方法Ⅱ,虽然理论上由不同立体像对计算出来的相对关系参数是一致的,但是由于误差的存在,实际得到的参数存在差别。
方法Ⅰ和方法Ⅱ都必须提供相机内外参数的初值,试验均采用二维DLT变换解法[10]进行参数初值的线性估计。此外,虽然本文试验均只针对平面标定场进行设计,但对于三维控制场,除参数初值的估计方法存在区别外,该标定方法仍然适用。
3.1 模拟数据试验首先给定一组具有固定相对关系参数的立体相机参数和一组平面控制点数据,然后根据共线方程分别计算出左右相机的像点坐标,生成立体相机标定的模拟数据。其中,立体相机参数包括左右相机的主距f;像主点坐标x0和y0;畸变参数k1、k2、p1和p2;以及8个立体像对的左相机外方位元素Xs、Ys、Zs、φ、ω和κ。这8个立体像对都满足的左右相机固定的相对参数Xc、Yc、Zc、φc,ωc和κc的大小分别为730.783 mm、2.442 mm、-190.171 mm、-0.494 311 rad、-0.014 348 rad和-0.034 307 rad。此外,模拟的平面控制点位于均匀分布的15×15的平面控制格网交点,格网的间距为60 mm,平面控制格网在X方向和Y方向的坐标范围均为0~840 mm;模拟像平面的大小为1280像素×1024像素,像素大小为0.005 2 mm。
为了模拟实际含有误差的数据,本文对模拟数据中的控制点和影像点坐标均加入均值为零的服从正态分布的随机误差。对于像点坐标,本文加入8种不同的误差,方差分别为0.0像素、0.05像素、0.10像素、0.20像素、0.50像素、1.00像素、1.50像素 和2.00像素,分别记为I1~I8。对于控制点坐标,本文也加入4种不同的误差,方差分别为0.0 mm、0.1 mm、0.2 mm和0.5 mm,分别记为C1~C4。这些含有不同误差的像点数据和控制点数据两两组合,可以生成32组不同的模拟数据。
对生成的32组模拟数据,分别利用方法Ⅰ和方法Ⅱ进行立体相机标定试验。将标定结果与模拟数据的真实参数进行比较。表 1和表 2分别表示在控制点没有误差(控制点误差为C1),像点误差为I1~I8时,采用方法Ⅰ和方法Ⅱ估计的立体相机固定相对关系参数的误差大小。
| 噪声 | X c/mm | Y c/mm | Z c/mm | φ c/rad | ω c/rad | κ c/rad |
| I 1 | 0.000 038 | 0.000 109 | 0.000 145 | 0.000 000 | 0.000 000 | 0.000 001 |
| I 2 | 0.006 321 | 0.011 051 | 0.177 980 | 0.000 194 | 0.000 189 | 0.000 004 |
| I 3 | 0.112 990 | 0.058 307 | 0.444 340 | 0.000 159 | 0.000 282 | 0.000 113 |
| I 4 | 0.046 778 | 0.173 810 | 0.239 350 | 0.000 038 | 0.001 361 | 0.000 244 |
| I 5 | 0.241 730 | 0.318 080 | 0.996 660 | 0.000 181 | 0.000 807 | 0.000 110 |
| I 6 | 0.764 340 | 0.275 620 | 3.679 900 | 0.004 050 | 0.000 350 | 0.000 003 |
| I 7 | 0.645 130 | 0.637 970 | 6.293 000 | 0.010 900 | 0.006 951 | 0.001 714 |
| I 8 | 0.239 810 | 0.452 560 | 3.354 400 | 0.004 457 | 0.002 826 | 0.000 501 |
| 噪声 | X c/mm | Y c/mm | Z c/mm | φ c/rad | ω c/rad | κ c/rad |
| I 1 | 0.000 653 | 0.001 349 | 0.000 997 | 7.5E-07 | 5E-07 | 5E-07 |
| I 2 | 0.177 888 | 0.080 036 | 0.961 041 | 9.85E-05 | 0.000 304 | 4.58E-05 |
| I 3 | 0.356 906 | 0.225 673 | 1.068 464 | 0.000 125 | 0.000 149 | 7.59E-05 |
| I 4 | 0.404 063 | 0.753 035 | 0.905 811 | 0.000 484 | 0.001 464 | 0.000 232 |
| I 5 | 1.208 289 | 0.706 923 | 1.288 03 | 0.001 441 | 0.000 884 | 0.000 291 |
| I 6 | 4.475 248 | 1.865 947 | 7.284 798 | 0.002 63 | 0.002 688 | 0.000 496 |
| I 7 | 4.649 405 | 4.492 502 | 11.044 39 | 0.004 742 | 0.007 192 | 0.001 582 |
| I 8 | 3.823 082 | 4.660 487 | 6.928 167 | 0.006 06 | 0.003 07 | 0.001 003 |
表 2给出了方法Ⅱ估计的固定相对关系参数的误差大小的均值,反映了方法Ⅱ的标定误差。对比表 1和表 2可以看出,在不同大小的像点误差下,方法Ⅰ的误差在整体上远小于方法Ⅱ的误差(均值),并且随着像点误差的增大,两者的差异逐渐增大。此外,表 2给出的是误差的均值,所以方法Ⅱ的个别误差在具体情况下会远远大于表中所给的值。因此方法Ⅰ比方法Ⅱ具有更高的精度和更强的稳健性。
图 2表示控制点和像点坐标分别在不同的误差下,由方法Ⅰ和方法Ⅱ估计得到的Xc和主距f的误差。参数误差指的是参数的估计值与真值之间的差。对于方法Ⅱ,只将其中一组参数的误差在图中显示。不同的线代表控制点的不同误差,即C1~C4,其方差依次是0.0 mm、0.1 mm、0.2 mm、0.5 mm。

|
| 图 2 相机标定参数误差 Fig. 2 Errors of the stereo-camera calibration |
对比图 2的左边和右边,可以看出虽然在像点误差和控制点误差都很小的条件下,方法Ⅰ和方法Ⅱ差别不显著。这是因为:方法Ⅰ将相机间的固定相对关系作为强制约束条件加到相机标定的平差系统中,从而增加了平差的多余观测数,使平差系统的可靠性增强,但同时也导致平差系统的自由度减少,平差未知数被限制在一个较低维的空间中。
图 2同时也表明,随着像点误差的增大,方法Ⅱ的误差逐渐比方法Ⅰ大,因而方法Ⅰ的精度整体上高于方法Ⅱ,且稳健性更强。
本文在模拟数据生成的225个控制点中,保留其中均匀分布的71个点作为检查点。表 3表示控制点没有误差,像点误差分别为I1~I8时的检查点中误差以及反投影像点中误差(检查点真值直接投影到影像上)。表 3还说明当控制点误差为零,像点误差水平为I1~ I3时,两种方法结果都有很高的检查点精度,没有显著差别。但是随着像点坐标误差的增大,方法Ⅰ的检查点和反投影像点中误差逐渐小于方法Ⅱ。
| 噪声 | 方法Ⅰ | 方法Ⅱ | ||||||
| RMS_I /像素 |
RMS_X /mm |
RMS_Y /mm |
RMS_Z /mm |
RMS_I /像素 |
RMS_X /mm |
RMS_Y /mm |
RMS_Z /mm |
|
| I 1 | 0.004 | 0.000 | 0.000 | 0.000 | 0.002 | 0.000 | 0.000 | 0.000 |
| I 2 | 0.382 | 0.067 | 0.032 | 0.081 | 0.382 | 0.067 | 0.032 | 0.080 |
| I 3 | 0.377 | 0.053 | 0.029 | 0.068 | 0.376 | 0.053 | 0.029 | 0.068 |
| I 4 | 0.261 | 0.073 | 0.036 | 0.096 | 0.263 | 0.075 | 0.036 | 0.097 |
| I 5 | 0.553 | 0.123 | 0.052 | 0.159 | 0.560 | 0.125 | 0.053 | 0.162 |
| I 6 | 1.013 | 0.138 | 0.075 | 0.182 | 1.018 | 0.137 | 0.076 | 0.180 |
| I 7 | 1.489 | 0.159 | 0.089 | 0.215 | 1.521 | 0.172 | 0.093 | 0.232 |
| I 8 | 1.893 | 0.195 | 0.097 | 0.257 | 1.927 | 0.200 | 0.098 | 0.262 |
采用了1.1节图 1(a)所示的双目视觉设备,从不同的位置和方向,获取了关于平面标定板8个立体像对,然后对标定板上的控制点影像进行精密提取和识别,其结果用于立体相机标定试验。其中立体相机左右相机的焦距均约为12 mm;获取的影像大小为1280像素×1024像素;像素大小为0.005 2 mm;拍摄距离约为500 mm;标定板的有效范围约为180 mm×220 mm;标定板上相邻两个标志点的距离为20 mm。
共提取并识别出均匀分布的99个标志点的影像坐标,其中均匀分布的33个作为检查点,其余的作为控制点。试验结果表明本文方法检查点反投影像点中误差为0.27像素,而方法Ⅱ为0.18像素;方法Ⅰ的检查点在X、Y和Z 3个方向上的中误差分别为0.021 1 mm、0.046 3 mm和0.031 3 mm,而方法Ⅱ则分别为0.022 2 mm、0.034 5 mm和0.034 4 mm。
首先,相机地面分辨率约为0.22 mm,因此两种方法都能达到子像素的精度,但是方法Ⅰ的反投影像点中误差要大于方法Ⅱ。其原因跟模拟数据试验一样,也是固定相对关系元素约束条件的引入导致平差系统自由度减小的缘故。
其次,方法Ⅰ检查点中误差只在X和Z方向上略小于方法Ⅱ,而在Y方向上略大于方法Ⅱ,其主要的原因是标定板的标志点事先没有进行精密地量测,检查点的误差本身比较大。此外,注意到两种方法的检查点中误差差别在几个微米以内,因此要使检查点中误差能够反映出两种方法的精度差别,就要求检查点的精度在微米以内,要进行如此精密的测量是比较困难的。
为了对方法Ⅰ的性能进行进一步检验,表 4分别列出了两种方法的固定相对关系参数估计值。
| 方法 | X c /mm | Y c /mm | Z c /mm | φ c /rad | ω c /rad | κ c/rad | |
| Ⅱ | |||||||
| Ⅰ | 317.82 | -0.37 | -97.29 | -0.562 720 | -0.003 766 | 0.009 110 | |
| Pair1 | 317.65 | -1.24 | -99.73 | -0.565 456 | -0.003 274 | 0.009 578 | |
| Pair 2 | 318.64 | 1.44 | -100.54 | -0.567 675 | -0.007 939 | 0.009 716 | |
| Pair 3 | 316.37 | -4.65 | -98.28 | -0.562 619 | 0.002 724 | 0.012 974 | |
| Pair 4 | 318.67 | -2.49 | -99.35 | -0.567 693 | -0.000 798 | 0.010 796 | |
| Pair 5 | 320.15 | 1.84 | -101.40 | -0.571 580 | -0.008 821 | 0.007 820 | |
| Pair 6 | 317.58 | -0.66 | -98.78 | -0.565 270 | -0.004 275 | 0.008 448 | |
| Pair 7 | 316.49 | 0.16 | -99.03 | -0.563 694 | -0.005 715 | 0.008 753 | |
| Pair 8 | 318.46 | -1.49 | -100.02 | -0.567 008 | -0.002 904 | 0.010 573 |
表 4表明方法Ⅱ在同一次标定平差结束后,利用不同立体像对估计出来的8组固定相对关系参数具有较大的波动,例如Yc的波动幅度达到6.5 mm;ωc的波动幅度达到0.01 rad(约为0.6°);基线长度波动幅度则达到4.5 mm。方法Ⅰ由于固定相对关系的引入,由不同像对估计的固定相对关系参数是一致的,因而不存在参数波动问题。因此这进一步验证方法Ⅰ能够有效地进行立体相机的精密标定,且稳健性比方法Ⅱ强。
4 结 论试验表明固定相对关系约束条件的引入使本文方法具有更强的稳健性,并在一定程度上具有更高的标定精度。在实际应用中,为了达到较好的标定精度,需要根据实际的情况,选择合适的标定板,使其成像尽可能充满整个画幅。而为了进一步提高标定精度,可以通过进一步考虑增拍照的像对数实现,也可以通过考虑增加畸变参数以更准确地反映相机的畸变模型(满足大像幅相机的标定需要)实现。
此外,由于采用附有约束条件的间接法平差模型,所以本文的约束条件表达式以及标定方法可以在不改变像点观测误差方程形式的条件下,通过增加一类形式统一的约束条件方程,很方便地推广到由多个相机组成的立体相机测量系统的标定中。
| [1] | BRUNO F, BIANCO G, MUZZUPAPPA M, et al. Experi-mentation of Structured Light and Stereo Vision for Underwater 3D Reconstruction[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2011, 66 (4): 508-518. |
| [2] | DI K, XU F, WANG J, et al. Photogrammetric Processing of Rover Imagery of the 2003 Mars Exploration Rover Mission[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2008, 63 (2): 181-201. |
| [3] | ZHENG Shunyi, WANG Ruirui, CHEN Changjun, et al. 3D Measurement and Modeling Based on Stereo-camera[C]//The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Beijing:[s.n.], 2008. |
| [4] | SALONIA P, SCOLASTICO S, POZZ A, et al. Multi-scale Cultural Heritage Survey: Quick Digital Photogrammetric Systems[J]. Journal of Cultural Heritage, 2009, 10(1): 59-64. |
| [5] | ERGUN B. An Expert Measurement System for Photogrammetric Industrial Application[J]. Measurement, 2006, 39(5): 415-419. |
| [6] | MAIMONE M, JOHNSON A, CHENG Y, et al. Autonomous Navigation Results from the Mars Exploration Rover (MER) Mission[C]//Proceedings of the 9th International Symposium on Experimental Robotics. Singapore:[s.n.],2006. |
| [7] | TSAI R Y. A Versatile Camera Calibration Technique for High-accuracy 3D Machine Vision Metrology Using Off-the-shelf TV Cameras and Lenses [J]. IEEE Journal of Robotics and Automation, 1987, 3(4):323-344. |
| [8] | ZHANG Zhengyou. A Flexible New Technique for Camera Calibration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330-1334. |
| [9] | XIE Wenhan, ZHANG Zuxun. Camera Calibration Based on Vanishing Points of Multi-image [J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(4): 335-340. (谢文寒,张祖勋. 基于多像灭点的相机定标[J]. 测绘学报, 2004, 33(4): 335-340.) |
| [10] | ZHANG Yongjun, ZHANG Zuxun, ZHANG Jianqing. Camera Calibration Using 2D-DLT and Bundle Adjustment with Planar Scenes[J]. Geomatics and Information Science of Wuhan University, 2002, 27(6): 566-571.(张永军, 张祖勋, 张剑清. 利用二维DLT及光束法平差进行数字摄像机标定[J]. 武汉大学报: 信息科学版,2002, 27(6): 566-571. ) |
| [11] | LIGHT D L. New Camera Calibration System at the U.S. Geological Survey[J]. Photogrammetric Engineering and Remote Sensing, 1992, 58(2): 185-188. |
| [12] | BROWN D C. Close-range Camera Calibration[J]. Photogrammetric Engineering and Remote Sensing, 1971, 37(8): 855-866. |
| [13] | KIM, W S, ANSAR A I, STEELE R D. Rover Mast Calibration, Exact Camera Pointing, and Camera Handoff for Visual Target Tracking[C]//Proceedings of 12th International Conference on Advanced Robotics.Seattle:[s.n.], 2005: 384-391. |
| [14] | ZHENG Shunyi, GUO Baoyun, LI Cailin. 3D Reconstruction and Inspection of Cylinder Based on Geometric Model and Generalized Point Photogrammetry[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 477-482.(郑顺义, 郭宝云, 李彩林. 基于模型和广义点摄影测量的圆柱体自动三维重建与检测[J]. 测绘学报, 2011, 40(4):477-482. ) |
| [15] | HARTLEY R. Estimation of Relative Camera Positions for Uncalibrated Cameras [C] // Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. [S.l.]:Springer,1992: 761-764. |
| [16] | CERVERI P, BORGHESE N A, PEDOTTI A. Complete Calibration of a Stereo Photogrammetric System through Control Points of Unknown Coordinates[J]. Journal of Biomechanics, 1998, 31(10): 935-940. |
| [17] | DAVID D, ANDREW Z, RADU H. Stereo Autocalibration from One Plane[C]//Proceedings European Conference Computer Vision. Dublin:[s.n.], 2000. |
| [18] | MALM H, HEYDEN A. Stereo Head Calibration from a Planar Object[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition,Miami:[s.n.],2001: 657-662. |
| [19] | TAN Xiaojun, YU Zhi, LI Jun. An Improved Method of Stereo Camera Calibration[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(2): 138-142. (谭晓军, 余志, 李军. 一种改进的立体摄像机标定方法[J]. 测绘学报, 2006, 35(2): 138-142.) |
| [20] | LERMA J L, NAVARRO S, CABRELLES M, et al. Camera Calibration with Baseline Distance Constraints[J]. Photogrammetric Record, 2010, 25(130): 140-158. |
| [21] | MEMONY Q, KHAN S. Camera Calibration and Three-dimensional World Reconstruction of Stereo-vision Using Neural Networks[J]. International Journal of Systems Science, 2001, 32(9):1155-1159. |
| [22] | ZHANG Jianqing, PAN Li, WANG Shugen. Photogrammetry[M]. Wuhan: Wuhan University Press, 2003. (张剑清, 潘励, 王树根. 摄影测量学[M]. 武汉: 武汉大学出版社, 2003. ) |
| [23] | FENG Wenhao. Close-range Photogrametry[M]. Wuhan: Wuhan University Press, 2002. (冯文灏. 近景摄影测量学[M]. 武汉: 武汉大学出版社, 2002. ) |
| [24] | Wuhan Technical University of Surveying and Mapping. Error Theory and Foundation of Surveying Adjustment[M]. Wuhan: Wuhan University Press, 2003. (武汉大学测绘学院测量平差科学组. 误差理论与测量平差基础[M]. 武汉: 武汉大学出版社,2003. ) |
| [25] | LI Deren, YUAN Xiuxiao. Error Processing and Reliability Theory[M]. Wuhan: Wuhan University Press, 2002. (李德仁, 袁修孝. 误差处理与可靠性理论[M]. 武汉: 武汉大学出版社, 2002.) |













