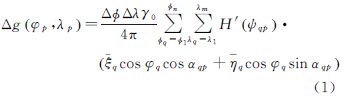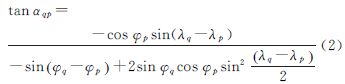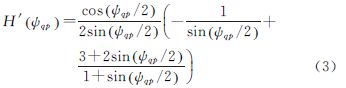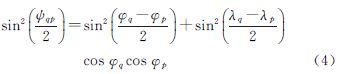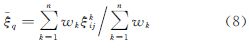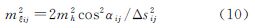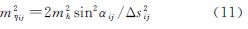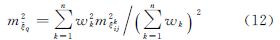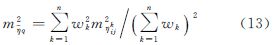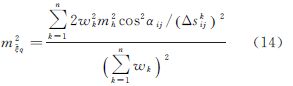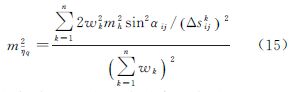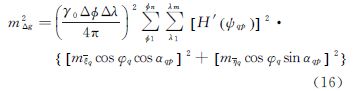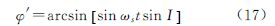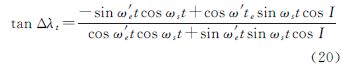2. 地理信息工程国家重点实验室,陕西 西安 710054;
3. 信息工程大学 地理空间信息学院,河南 郑州 450052
2. National Key Laboratory of Geo-information Engineering,Xi’an 710054,China;
3. Geo-information Institute,Information Engineering University,Zhengzhou 450052,China
1 引 言
卫星测高是20世纪后期发展起来的新型空间对地观测技术,它利用星载雷达测高仪测量卫星到海面的距离、有效波高和后向散射,从宇宙空间大规模探测海洋重力场、海洋潮汐、海洋环流、海面地形、海洋深度、海洋风场等海洋环境信息,是近几十年来海洋环境信息最主要、最有价值的观测手段。随着经济技术水平的提高,我国已启动HY-2等卫星测高计划,亟需分析卫星测高误差对海洋重力场反演、海洋环流预报等卫星测高应用成果的影响,从而为我国卫星测高系统论证设计提供技术支撑。
卫星测高探测海洋重力场的精度主要受两大因素的影响,分别是海面高测量误差和海洋重力场反演方法。当前,国际上利用卫星测高数据反演海洋重力场的方法主要有5种[1]:① 最小二乘配置法[2];② Stokes公式逆运算法[3];③ Hotine公式逆运算法[4];④ 直接求解法[5];⑤ 垂线偏差方法[6, 7]等。其中,最小二乘配置法需要预先确定各参量之间的协方差阵并解算大型矩阵,Stokes、Hotine公式的逆运算法易受动力海面地形模型误差的影响,而直接求解法在理论上存在一些近似。由于海面高的一次差分技术可以有效减弱动力海面地形、测高卫星径向轨道等系统误差的影响,精确计算大地水准面在经、纬度方向的梯度,从而精确确定海洋大地水准面上的测高垂线偏差。另一方面,根据物理大地测量的边值理论,各扰动场元之间存在固定的函数关系[8, 9]。因此,可以利用大地水准面上高精度的测高垂线偏差计算海洋上高精度的大地水准面、重力异常等扰动场元。上述理论即为卫星测高中的“垂线偏差法”,它为利用卫星测高资料反演高精度、高分辨率的海洋重力场提供了理论依据,标志着卫星测高技术在大地测量中的应用逐步趋于成熟。本文将采用“垂线偏差法”,根据逆Vening-Meinesz公式反演海洋重力场理论,定量分析卫星测高误差对重力场反演的影响。
卫星测高误差可分为3类[10, 11, 12]:仪器误差、环境改正误差和径向轨道误差。它们都是由系统误差和偶然随机误差组成,而依据海面高计算方法可知,上述误差将直接传递为海面高误差。当根据逆Vening-Meinesz公式反演海洋重力场时,是利用海面高差而非海面高直接推估海洋重力场,它有效减弱海面高观测值中系统误差的影响,这也是逆Vening-Meinesz公式的先进性所在。但逆Vening-Meinesz公式不能消除随机误差的影响,因此,定量分析卫星测高中的随机误差对海洋重力场反演的影响显得非常必要。
2 误差传播逆Vening-Meinesz公式反演海洋重力场的离散解析公式[13]为
式中,(φp,λp)是重力异常反演值Δg(φp,λp)所在格网中心p的球面坐标;(φq,λq)为平均垂线偏差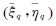 所在格网中心q的球面坐标;Δφ、Δλ为格网间隔;γ0为正常重力; αqp为从q到p的方位角,其计算方法如下
H′(Δψqp)为核函数,其大小仅同p、q的空间位置有关,其计算方法为
而格网上的平均垂线偏差可根据以下方法计算得到:假设hi、hj为测高卫星沿轨迹相邻的两观测点的海面高;Δsij为两观测点之间的距离;αij为从采样点i到采样点j的方位角,可根据公式(2)计算得到; εij是沿迹方向从采样点i到采样点j的垂线偏差或海面坡度,则
然后,将离散的垂线偏差(ξij,ηij)作格网化处理就可以得到流动格网上的平均垂线偏差(ξq,ηq)
式中,wk为观测点的权函数,该权函数是测量点相对于格网中心的空间方位的函数;n为格网p内离散的垂线偏差数目。根据卫星测高原理,卫星测高误差将直接转化为海面高误差。假设卫星测高误差中的随机误差为mh,且这些随机误差之间相互独立,则根据误差传播定律[14, 15]并综合式(5)—式(9)可得
所在格网中心q的球面坐标;Δφ、Δλ为格网间隔;γ0为正常重力; αqp为从q到p的方位角,其计算方法如下
H′(Δψqp)为核函数,其大小仅同p、q的空间位置有关,其计算方法为
而格网上的平均垂线偏差可根据以下方法计算得到:假设hi、hj为测高卫星沿轨迹相邻的两观测点的海面高;Δsij为两观测点之间的距离;αij为从采样点i到采样点j的方位角,可根据公式(2)计算得到; εij是沿迹方向从采样点i到采样点j的垂线偏差或海面坡度,则
然后,将离散的垂线偏差(ξij,ηij)作格网化处理就可以得到流动格网上的平均垂线偏差(ξq,ηq)
式中,wk为观测点的权函数,该权函数是测量点相对于格网中心的空间方位的函数;n为格网p内离散的垂线偏差数目。根据卫星测高原理,卫星测高误差将直接转化为海面高误差。假设卫星测高误差中的随机误差为mh,且这些随机误差之间相互独立,则根据误差传播定律[14, 15]并综合式(5)—式(9)可得
将式(10)、式(11)分别代入式(12)、式(13)可得
而根据式(1)可得重力异常反演误差mΔg的计算方法为
在离散垂线偏差作格网化处理的过程中,鉴于测高卫星的轨道参数确定了垂线偏差的位置,测量环境决定了测量数据是否有效,使得各格网中离散垂线偏差的数目、空间位置仅同测高卫星的轨道参数和测量环境有关。故在轨道参数和测量环境不变的情况下,式(14)、式(15)中的离散垂线偏差数目n、权函数wk、方位角αij和采样间距Δsijk不会随其他因素而改变;海洋重力异常反演误差mΔg与格网上的平均垂线偏差误差(mξq,mηq)或离散点上海面坡度εij的误差成正比,而离散点上海面坡度εij的误差是由海面高误差和采样差分的间隔联合决定的。
3 试验分析高精度、高分辨率是卫星测高探测海洋重力场的主要发展方向,测高资料的精度和分辨率限定了海洋重力场反演的精度和分辨率。当前,国际测高卫星的仪器误差约±2cm,环境误差约±4cm,轨道径向误差约±5cm;卫星测高资料及其反演海洋重力场的最高分辨率达2′×2′,精度为±(7~14)mGal[16, 17, 18, 19](1Gal=10-2 m/s2)。为了定量分析卫星测高随机误差对重力场反演的影响,本文根据测高卫星升(降)弧段沿赤道方向的间距与测高资料分辨率之间的对应关系,模拟了轨道倾角为98.5°,测高资料覆盖81.5°S—81.5°N、0°E—360°E且分辨率为1′×1′、2′×2′、3′×3′、5′×5′时测高卫星的轨道特征,分别推估了2cm、8cm卫星测高随机误差引发的海洋重力异常反演误差。
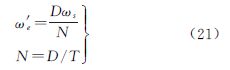
3.1 计算测高卫星星下点轨迹假设轨道升交点的经度为λ0、轨道倾角为I、交点周期为T、覆盖周期为D、卫星平均角速度为ωs、轨道升交点相对于经度零点的进动率为ω′e、N为一覆盖周期内卫星运行的圈数、时刻t0=0,根据卫星大地测量知识[20]可知,t时刻(由t0起算)卫星的地心纬度φ′由下式计算
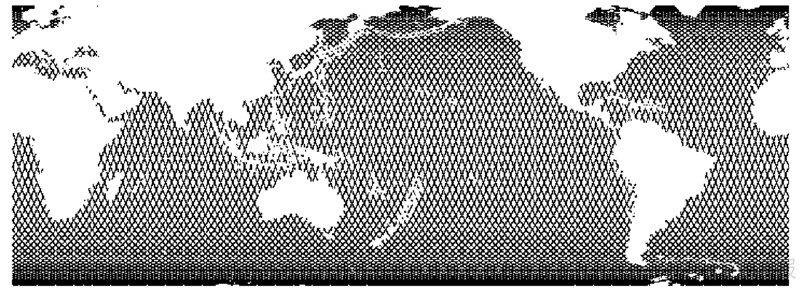
而t时刻卫星的经度λ由下式算得根据式(17)—式(21),本文计算了轨道倾角为98.5°,轨道间距为1′、2′、3′、5′时,测高卫星的星下点轨迹(如图 1所示)。
|
| 图 1 测高卫星正常点轨迹示意图 Fig. 1 The sketch map of atimetry satellite orbit tracks on the ground |
在相同的观测条件下,测高卫星的轨道根数不仅决定了卫星测高的空间分辨率,也决定了式(14)中权函数wk、方位角αij和采样间距Δsijk。本文根据式(10)—式(16),逐一计算了2cm、8cm测高随机误差在分辨率为1′×1′、2′×2′、3′×3′、5′×5′时引发的重力异常推估误差。鉴于式(16)理论上要求全球积分,而测高卫星的轨道倾角为98.5°,其星下点轨迹覆盖范围为全球81.5°S—81.5°N海域,为此,本文将全球其他区域的测高误差约定为零,详细的计算结果见表 1。
| 重力场参数 | 分辨率 | 海面高误差
/cm |
海面坡度误差
/μrad |
反演误差
/mGal |
| 重力异常 | 1′×1′ | 2 | 15.8 | 3.9 |
| 2′×2′ | 7.9 | 2.0 | ||
| 3′×3′ | 5.2 | 1.3 | ||
| 5′×5′ | 3.2 | 0.8 | ||
| 1′×1′ | 8 | 62.9 | 15.9 | |
| 2′×2′ | 31.4 | 8.0 | ||
| 3′×3′ | 21.0 | 5.2 | ||
| 5′×5′ | 12.6 | 3.2 |
本文研究了卫星测高误差对海洋重力场反演的影响,导出了卫星测高随机误差在海洋重力异常推估中的误差传播公式,定量分析了测高随机误差引发的海洋重力异常误差。研究结果表明,当测高卫星轨道倾角为98.5°,采用逆Vening-Meinesz公式反演海洋重力场时:
(1) 2cm测高随机误差引发的1′×1′海洋重力异常反演误差为±3.9mGal。
(2) 海洋重力异常反演误差与测高随机误差呈正比变化,与海洋重力异常的空间分辨率成反比变化。
上述技术理论成果可为我国卫星测高系统论证设计过程中的误差指标分配提供技术参考。需要说明的是,本文对卫星测高随机误差仅作简要建模,通过深入开展测高误差分析建模有望更精确评估其对海洋重力场反演的影响。
| [1] | WANG Haiying, WANG Guangyun. Inversion of Gravity Anomalies from Along-track Vertical Deflections with Satellite Altimeter Data and Its Applications[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(1): 21-26. (王海瑛,王广运. 卫星测高数据的沿轨迹重力异常反演法及其应用[J]. 测绘学报,2001,30(1): 21-26.) |
| [2] | BASIC T, RAPP R H. Ocean Wide Prediction of Gravity Anomalies and Sea Surface Heights Using Geos-3 Seasat, Geosat Altimeter Data and ETOPO5U Bathymetric Data[R]. Columbus: Ohio State University, 1992. |
| [3] | HUANG Motao, ZHAI Guojun, GUAN Zheng, et al. On the Recovery of Gravity Anomalies from Altimeter Data[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(2): 179-184. (黄谟涛,翟国君,管铮, 等. 利用卫星测高数据反演海洋重力异常研究[J]. 测绘学报,2001,30(2): 179-184.) |
| [4] | ZHANG C, SIDERIS M G.Oceanic Gravity by Analytical Inversion of Hotines Formula[J]. Marine Geodesy, 1996, 19(2): 115-36. |
| [5] | ZHANG Changyou, BLAIS J. Recovery of Gravity Disturbances from Satellite Altimetry by FFT Techniques: A Synthetic Study[J]. Manuscripta Geodaetica, 1993, 18(3): 158-170. |
| [6] | HWANG C, KAO E C, PARSONS B. Global Derivation of Marine Gravity Anomalies from Seasat, Geosat, ERS-1 and TOPEX/Poseidon Altimeter Data[J]. Geophysical Jounal International, 1998, 134(2): 449-459. |
| [7] | LI Jiancheng, NING Jinsheng, CHEN Junyong, et al. Determination of Gravity Anomalies over the South China Sea by Combination of TOPEX/Poseidon ERS2 and Geosat Altimeter Data[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(3): 197-202. (李建成, 宁津生, 陈俊勇, 等. 联合TOPEX/Poseidon ERS2 和Geosat卫星测高资料确定中国近海重力异常[J]. 测绘学报,2001, 30(3): 197-202.) |
| [8] | HEISKANEN W A, MORITZ H. Physical Geodesy[M]. San Francisco: Freeman W H and Company, 1967. |
| [9] | YU Jinhai, ZHANG Chuanding. A Solution Method for the Satellite Altimetry Problem with the Spherical Harmonic Series[J]. Chinese Journal of Geophysics, 2005, 48(3): 561-566. (于锦海,张传定. 卫星测高混合边值问题的球谐级数解法[J]. 地球物理学报, 2005, 48(3): 561-566.) |
| [10] | AVISO. AVISO and PODAAC User Handbook: IGDR and GDR Jason Products[M]. 2nd ed. [S.l.]: AVISO, 2004. |
| [11] | DONG Xiaojun, HUANG Cheng. Monitoring Global Mean Sea Level Variation with TOPEX/Poseidon Altimetry[J]. Acta Geodaetica et Cartographica Sinica, 2000, 29(3): 266-272. (董晓军,黄珹. 利用TOPEX/Poseidon卫星测高资料监测全球海平面变化[J]. 测绘学报, 2000, 29(3): 266-272.) |
| [12] | HU Jianguo, LI Jiancheng, DONG Xiaojun. Using Satellite Altimetry Technique for Monitoring the Sea Level Change[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(4): 316-321. (胡建国,李建成,董晓军. 利用卫星测高技术监测海平面变化[J]. 测绘学报, 2001, 30(4): 316-321.) |
| [13] | HWANG C. Inverse Vening Meinesz Formula and Deflection-geoid Formula: Applications to the Predictions of Gravity and Geoid over the South China Sea[J]. Journal of Geodesy, 1998, 72(3): 304-312. |
| [14] | YANG Y. Robust Bayesian Estimation[J]. Bulletin Geodesique, 1991, 65(3): 145-150. |
| [15] | YANG Y. Robust Estimation for Dependent Observations[J]. Manuscripta Geodeatica, 1994, 19(1): 10-17. |
| [16] | LI Jiancheng, NING Jinsheng, CHEN Junyong, et al. Geoid Determination in China Sea Areas[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(2): 114-119. (李建成, 宁津生, 陈俊勇, 等. 中国海域大地水准面和重力异常的确定[J]. 测绘学报, 2003, 32(2): 114-119.) |
| [17] | PENG Fuqing, ZHANG Ruihua, SHI Pan, et al. Marine Geoid from Satellite Altimeter Data[J]. Chinese Journal of Geophysics, 2003, 46(4): 462-466. (彭富清,张瑞华,石磐,等. 基于卫星测高的海域大地水准面[J]. 地球物理学报, 2003, 46(4): 462-466.) |
| [18] | ANDERSON O B,KNUDSEN P.Global Marine Gravity Field from the ERS-1 and Geosat Geodetic Mission Altimetry[J]. Journal of Geophysical Research: Ocean, 1998, 103(C4): 8129-8137. |
| [19] | SANDWELL D T. Marine Gravity Anomly from Geosat and ERS 1 Satellite Altimetry[J]. Journal of Geophysical Research, 1997, 102(B5): 10039-10054. |
| [20] | KAULA W K. Theory of Satellite Geodesy: Applications of Satellites to Geodesy[M]. New York: Dove Publication Inc, 1966. |