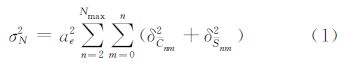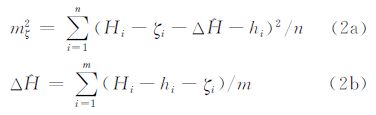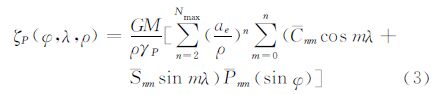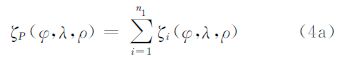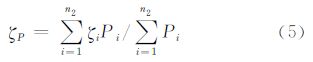2.同济大学 测绘与地理信息学院,上海 200092;
3.铁道第三勘察设计院集团有限公司 测绘分院,天津 300251
2.College of Surveying and Geo-informatics, Tongji University, Shanghai 200092,China;
3.Department of Surveying and Mapping, The Third Surveying and Design Institute Ltd C, Tianjin 300251, China
高分辨率、高精度的地球重力场模型在利用GPS技术快速确定正常高过程中发挥重要的作用[1, 2],随着CHAMP、GRACE和GOCE等重力卫星的成功实施,全球重力场模型的中低阶位系数的精度提高了约两个量级甚至更高[3, 4, 5, 6, 7, 8, 9, 10]。因此,如何综合利用由不同反演方法及数据源求得的具有不同精度及分辨率的地球重力场模型并分析其用于GPS正常高测量的精度,具有重要的现实意义。2008年EGM2008模型的公布,使得重力场模型所表示的全球大地水准面的精度和分辨率均达到了前所未有的水平,其分辨率约5′[11, 12, 13, 14, 15]。文献[16]分析表明,该模型在我国区域的整体精度约20 cm,华北地区高达9 cm[16],而EGM2008模型仅采用了由不足5年GRACE卫星数据获得的ITG-GRACE03S模型的有关信息。
近年来,国际相关科研机构发布了利用CHAMP、GRACE、GOCE、Lageos、SLR及地面重力测量等数据获得的一系列高精度的地球重力场模型。本文重点探讨ITG-GRACE2010S、AIUB-GRACE03S、EIGEN-6C、GOCO02S、DIR_R3、TIM_R3、SPW_R2、gif48以及EGM2008模型中低阶位系数的精度,特别是利用长时间GRACE和GOCE观测数据以及最新DTU10全球重力异常数据[17]对重力场模型精度的改进情况。通过分析不同模型不同频域所对应的位系数精度,探讨不同模型组合应用,提高区域模型高程异常精度的方法。
2 原理与方法2.1 地球重力场模型的精度评定方法
评价地球重力场模型精度的常用方法有两种:① 通过地球重力场位系数方差计算大地水准面的阶误差及其累积误差,该精度称为内符合精度;② 通过与已有高精度重力场模型比较,计算模型间位系数差值所对应的大地水准面差或通过已有的GPS/水准及地面重力等数据对其进行检核,该精度称为外符合精度。
若将地球重力场位系数方差或不同位系数间的差值表示成大地水准面累积误差的形式,则精度评定公式为
采用已有的GPS/水准数据评定模型精度的公式为
式中,Hi、ζi和hi分别为第i个点的大地高、模型高程异常和正常高;n为用于评价模型精度的GPS/水准点个数;Δ 为模型对应的似大地水准面和我国正常高基准的系统偏差;m为用于计算该偏差的GPS/水准点个数。值得注意的是,若采用相同的GPS/水准点计算Δ
为模型对应的似大地水准面和我国正常高基准的系统偏差;m为用于计算该偏差的GPS/水准点个数。值得注意的是,若采用相同的GPS/水准点计算Δ 和mζ,则公式(2a)中分母应取n-1(此时m=n);若不考虑偏差影响,则取Δ
和mζ,则公式(2a)中分母应取n-1(此时m=n);若不考虑偏差影响,则取Δ =0。
2.2 模型尺度参数ae对模型高程异常计算的影响
=0。
2.2 模型尺度参数ae对模型高程异常计算的影响不同地球重力场模型,如EGM2008、EIGEN-6C等,其尺度参数GM通常取GM=0.398 600 441 5E+15(引力常数与地球质量的乘积,本文所有模型GM均为此值),而尺度参数ae的取值不同,如EGM2008模型取ae=6 378 136.3 m,EIGEN-6C模型取ae=6 378 136.46 m等。为分析模型尺度参数ae的不同取值对模型高程异常计算的影响,现选择EGM2008模型作为参考模型,阶次取2160,沿经度113°从纬度-90°~90°每隔1°选取一个计算点,将ae=6 378 136.3 m作为参考值,其他几个常用取值的计算结果与参考值对应的结果比较,差值统计结果见表 1。结果表明,目前几个常用的ae数值对应的模型高程异常与参考值对应的模型高程异常的差异最大为3.0 mm,标准差为1.5 mm。值得说明的是,本文仅有AIUB-GRACE03S模型取ae=6 378 137 m,故不同模型间ae的差异对模型高程异常的影响值绝大部分不超过1 mm,因此,下文分析中可忽略不同模型尺度参数ae对结果的影响。
| mm | ||||
| ae取值/m | 最小值 | 最大值 | 平均值 | 标准差 |
| 6 378 136.46 | -1.0 | 1.0 | -0.2 | 0.5 |
| 6 378 136.60 | -2.0 | 1.0 | -0.3 | 0.7 |
| 6 378 137.00 | -3.0 | 2.0 | -0.6 | 1.5 |
根据Bruns公式,GPS点的模型高程异常可利用一定阶次的地球重力场模型计算[1, 16, 18]
式中,ρ、φ和λ分别为计算点P的地心向径、地心纬度和经度;γP为点P的正常重力;Cnm、Snm为完全规格化位系数,其中偶次带谐系数代表实际引力位与正常引力位的系数之差;Pnm(sin ψ)为完全规格化Legendre函数。目前诸多重力场模型的分辨率各不相同,特别是仅利用卫星跟踪数据(如GRACE卫星)只能获得中低阶重力场位系数,且一般都具有较高的精度,但其最高阶次一般不超过180阶,即使联合GOCE卫星跟踪数据,其最高阶次也不超过250。因此可考虑采用谱组合技术来确定GPS点的模型高程异常,即任意GPS点全频域的高程异常可表示为如下形式
式中,n1为全频域高程异常分解的频域数,一般取n1=3,即将全频域高程异常分为3部分: ζ1、ζ2和ζ3,其分别表示模型中低阶位系数、高阶和超高阶位系数以及模型截断误差对应的高程异常,模型截断误差可采用SRTM/DTM2006.0剩余地形模型计算[19, 20],该项在地形起伏大的地区影响较大,在平坦地区影响很小;另外两部分均可采用不同模型的不同阶次计算 式中,Nmin和Nmax分别为所采用模型的最低阶和最高阶;其他参数含义与式(3)相同。用式(4)计算任意点模型高程异常的方法称为简单谱组合方法,虽然采用简单谱组合方法可获得任意点的全频域的高程异常,但在不同区域,每个简单谱组合模型得到的高程异常的精度也会不同,因此,可采用对多个简单谱组合模型求得的高程异常进行加权处理,以提高高程异常计算的精度和稳定性 式中,取权Pi=C/σi2,σi可利用若干个GPS/水准数据按式(2)计算,C为常数;n2为计算所采用简单谱组合模型的个数;ζi为每个简单谱组合模型的计算结果。用式(5)计算GPS点高程异常的方法称为加权谱组合方法。 3 9种地球重力场模型的精度分析与比较截至2011年12月,国际相关科研机构先后发布了多达几十个高精度的地球重力场模型,最具代表性的模型有:ITG-GRACE2010S、AIUB-GRACE03S、EIGEN-6C、GOCO02S、DIR_R3、TIM_R3、SPW_R2、gif48以及EGM2008等。其中EGM2008及EIGEN-6C属于超高阶地球重力场模型,模型阶分别高达2190和1420。下文将分析这9个典型重力场模型的精度。
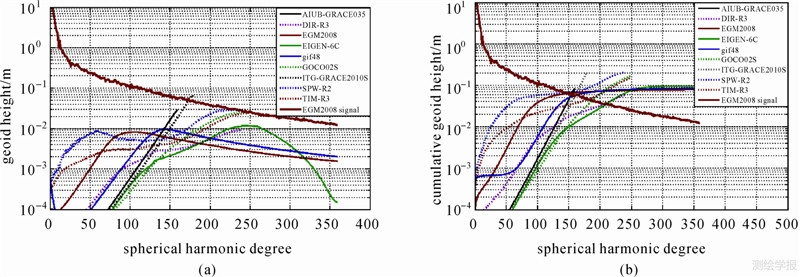
3.1 各重力场模型大地水准面精度分析图 1为由各重力场模型位系数方差按式(1)求得的大地水准面的阶误差和累积误差,即为各模型的内符合精度。ITG-GRACE2010S、AIUB-GRACE03S、EIGEN-6C、GOCO02S及DIR_R3模型中低阶位系数与EGM2008模型相比。各模型大地水准面阶误差小于EGM2008模型所对应的阶次分别为:143、137、188、165和187,各模型大地水准面累积误差小于EGM2008模型所对应的阶次分别为:163、156、252、207和240。而TIM_R3和SPW_R2模型分别在65~165、83~150阶范围内的大地水准面阶误差小于EGM2008模型,SPW_R2模型大地水准面累积误差均大于EGM2008模型,TIM_R3模型大地水准面累积误差在79~210阶范围内小于EGM2008模型,主要因为这两个重力场模型都是仅利用短时间的GOCE观测数据求得。gif48模型大地水准面阶误差以及累积误差小于EGM2008模型的阶范围分别为9~128、28~202。由于EIGEN-6C、GOCO02S及DIR_R3模型是联合了GRACE卫星以及GOCE卫星重力梯度等数据获得的,100阶后,EIGEN-6C和GOCO02S模型的精度要优于ITG-GRACE2010S模型,DIR_R3模型精度也优于同阶次的gif48模型,说明GOCE卫星重力梯度数据能有效改善100阶后的重力位系数的精度。
|
| 图 1 各模型大地水准面阶误差(a)和大地水准面累积误差(b) Fig. 1 The degree error (a) and accumulative error (b) of geoid height for all models |
为了对上文给出的9种地球重力场模型不同阶次精度作进一步分析,选择我国东北某4条客运专线的高精度GPS/水准数据作试验,线路平均长度约200 km。共收集GPS/水准点430个,其中GPS为客运专线的CPI和CPII控制点,坐标基准为2000国家大地坐标系,水准测量为二等,高程基准为1985国家高程基准。分析过程分两步:第1步利用实测GPS数据分析各模型与EGM2008模型间的差异;第2步用实测GPS/水准数据分析各模型高程异常精度及可靠阶次。
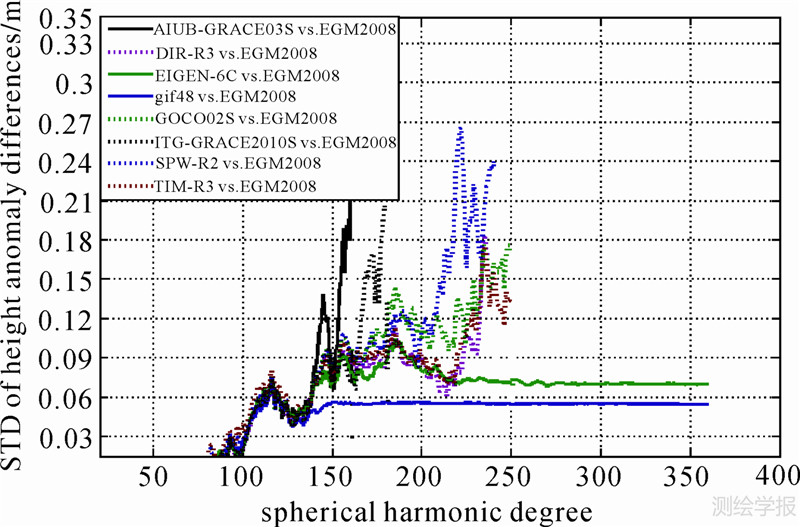
第1步是利用各模型不同阶次的位系数计算430个GPS点的模型高程异常,所有模型均与EGM2008模型对应值进行比较,差值的标准差见图 2。结果表明:① 前70阶各模型与EGM2008模型高程异常差异很小;② 在70~135阶内,各模型与EGM2008模型的差异几乎是一致的,意味这些模型精度相当,135阶后,gif48模型与EGM2008模型的差异及其变化较其他模型要小;③ 在135~220阶内,当模型阶次超过150阶后,AIUB-GRACE03S模型与EGM2008模型的差异迅速变大,而gif48模型与EGM2008模型的差异近乎常数,当模型阶次超过160阶后,ITG-GRACE2010S模型与EGM2008模型的差异迅速变大,当模型阶次超过180阶后,GOCO02S和SPW-R2模型与EGM2008模型的差异逐渐变大,且这两个模型与其他模型的差异也逐渐变大,其他模型与EGM2008模型的差异基本是一致的;④ 当模型阶次超过220阶后,EIGEN-6C模型与EGM2008模型的差异近乎常数,而DIR-R3和TIM-R3模型与EGM2008模型的差异逐渐变大;⑤ 虽然gif48和EIGEN-6C模型均使用了DTU10全球重力异常数据,但EIGEN-6C模型还增加了约6.7个月GOCE数据,这可能是在135~220阶范围内,两模型与EGM2008模型的差异不同的主要原因。
|
| 图 2 各模型不同阶次对应的模型高程异常与EGM2008对应结果差值的标准差 Fig. 2 STDs of height anomaly differences between all 9 GGMs and EGM2008 for different degrees |
第2步具体分析过程为:① 使用实测GPS/水准数据对各模型不同阶次的精度进行分析,为避免各模型的谱泄露,采用谱组合技术,即被分析模型所选择阶次以外的位系数均用EGM2008模型扩充到2160阶次,并忽略这些补充位系数对结果的影响,如被分析模型选择阶次为N,则N+1阶至2160阶用EGM2008位系数补充;② 由于测区地势起伏相对平坦,可不考虑RTM的影响;③ 各模型从60阶开始计算分析,每条线路均独立计算模型所对应的似大地水准面与我国高程基准的系统偏差,综合4条线路数据计算各模型不同阶次的精度,结果见图 3。

|
| 图 3 各模型从60阶到最高阶的模型高程异常与GPS/水准点高程异常差值的标准差 Fig. 3 TSTDs of height anomaly differences between model height anomaly from degree 60 to max degree and GPS/leveling height anomaly |
图 3结果表明:① AIUB-GRACE03S、DIR_R3、GOCO02S、ITG-GRACE2010S、SPW_R2以及TIM_R3模型可靠阶次分别为150、220、170、160、180以及210,判定的依据是当被评价模型达到一定阶次后其精度迅速变差,则该阶次即为模型可靠阶次(或信号丢失的阶次);② 当模型阶次为2~100阶时,所有模型与EGM2008模型精度相当;③ 当模型阶次为201~360阶时,EIGEN-6C和gif48模型精度与EGM2008模型相当,而当模型阶次为101~200阶时,两模型整体精度优于EGM2008模型;④ DIR_R3模型在101~210阶范围内整体精度优于EGM2008模型;⑤ GOCO02S、SPW_R2以及TIM_R3模型在101~170阶范围内与EGM2008模型精度相差不大,部分阶次精度要优于EGM2008模型。由于用于本文分析的模型来自不同的科研机构,计算方法也不尽相同,且在全球范围内EGM2008模型具有公认的较高精度,因此通过实测GPS数据或GPS/水准数据可基本判定一个模型的可靠阶次,且模型间可相互检核。
4 多类重力场模型联合确定GPS点正常高的精度分析本文所分析的9种地球重力场模型的分辨率及精度各不相同,为了充分挖掘各模型所蕴涵的重力场信息,在上文分析各重力场模型精度的基础上,本节将采用简单谱组合方法(获得的模型命名为组合模型)和加权谱组合方法(获得的模型命名为综合模型)求解任意GPS点的全频域高程异常并分析其精度。
4.1 简单谱组合方法精度分析简单谱组合方法是利用各模型精度较高的谱域位系数或可靠谱域位系数,其余谱域位系数用EGM2008模型补充至2160阶次,通过该简单组合模型从而获得任意GPS点全频域高程异常。
表 2给出了各模型确定的模型高程异常与430个GPS/水准实测高程异常的比较结果,其中“EIGEN-6C(1420)/EGM2008”表示EIGEN-6C与EGM2008模型进行简单谱组合,“1420”为EIGEN-6C所采用的阶次,“2160”为组合模型的最高阶次,其他情况依次类推。表 2结果表明:① 4条线路独立计算各模型对应的似大地水准面与我国高程基准的系统偏差(以下简称为高程系统偏差,即各模型所确定的模型高程异常与GPS/水准点确定的高程异常差值的平均值,见2.1节)后的精度比4条线路整体计算高程系统偏差的精度均有不同程度的提高,精度最高约提高34%,说明各模型对应的高程系统偏差在不同区域有所差异,消除这种差异可提高各GPS点模型高程异常精度;② EIGEN-6C模型比同阶次的EGM2008模型的整体精度要高,对应360、720、1420阶的模型精度分别为0.106 m、0.056 m和0.052 m,而与同阶次的gif48模型差异不大;③ 当各模型的阶次为2160时,EGM2008模型精度为0.059 m、EIGEN-6C(1420)/EGM2008模型的精度为0.052 m、gif48(360)/EGM2008模型的精度为0.051 m,其余组合模型的精度均优于0.050 m,但它们相互间的差异不大,组合模型比EGM2008模型精度提高至少12%,特别是各模型135阶与EGM2008模型的组合结果更好,说明各模型的中低阶位系数比EGM2008模型精度高,原因是这些模型均采用了更长时间的GRACE卫星观测数据或联合了GOCE卫星观测数据或采用了最新的DTU10全球重力异常数据。| m | ||||||||
| 所有线路计算一个整体偏差 | 每条线路独立计算偏差 | 精度提高/(%) | ||||||
| 地球重力场模型 | 阶次 | 最小值 | 最大值 | 标准差 | 最小值 | 最大值 | 标准差 | |
| EIGEN-6C | 360 | -0.404 | 0.312 | 0.118 | -0.366 | 0.312 | 0.106 | 10.2 |
| EGM2008 | 360 | -0.310 | 0.408 | 0.126 | -0.310 | 0.381 | 0.116 | 7.9 |
| gif48 | 360 | -0.327 | 0.290 | 0.123 | -0.327 | 0.282 | 0.113 | 8.1 |
| EIGEN-6C | 720 | -0.217 | 0.188 | 0.067 | -0.171 | 0.146 | 0.056 | 16.4 |
| EGM2008 | 720 | -0.194 | 0.254 | 0.077 | -0.158 | 0.199 | 0.065 | 15.6 |
| EIGEN-6C | 1420 | -0.163 | 0.165 | 0.063 | -0.127 | 0.131 | 0.052 | 17.5 |
| EGM2008 | 1420 | -0.165 | 0.274 | 0.074 | -0.165 | 0.219 | 0.059 | 20.3 |
| EIGEN-6C(1420)/EGM2008 | 2160 | -0.159 | 0.164 | 0.061 | -0.123 | 0.133 | 0.052 | 14.8 |
| EGM2008 | 2160 | -0.174 | 0.272 | 0.073 | -0.174 | 0.202 | 0.059 | 19.2 |
| gif48(360) /EGM2008 | 2160 | -0.168 | 0.155 | 0.065 | -0.138 | 0.124 | 0.051 | 21.5 |
| gif48(135) /EGM2008 | 2160 | -0.169 | 0.193 | 0.064 | -0.118 | 0.137 | 0.048 | 25.0 |
| EIGEN-6C(135) /EGM2008 | 2160 | -0.182 | 0.180 | 0.069 | -0.134 | 0.123 | 0.047 | 31.9 |
| AIUB_GRACE03S(135)/EGM2008 | 2160 | -0.174 | 0.187 | 0.073 | -0.115 | 0.148 | 0.048 | 34.2 |
| GOCO02S(135) /EGM2008 | 2160 | -0.179 | 0.186 | 0.069 | -0.124 | 0.128 | 0.047 | 31.9 |
| ITG_GRACE2010S(135)/EGM2008 | 2160 | -0.174 | 0.183 | 0.067 | -0.130 | 0.125 | 0.047 | 29.9 |
| DIR_R3(135) /EGM2008 | 2160 | -0.175 | 0.181 | 0.067 | -0.122 | 0.129 | 0.045 | 32.8 |
| TIM_R3(135) /EGM2008 | 2160 | -0.168 | 0.165 | 0.062 | -0.124 | 0.126 | 0.047 | 24.2 |
| SPW_R2(135) /EGM2008 | 2160 | -0.178 | 0.174 | 0.067 | -0.132 | 0.123 | 0.046 | 31.3 |
上文采用所有430个GPS/水准点对简单谱组合方法的精度进行了分析,但在实际应用中,若能实现综合各类重力场模型信息,用尽量少的GPS/水准点获取待求GPS点稳定的、高精度的高程异常才更具有现实意义,故本文探讨采用加权谱组合方法实现该目的。其过程是先利用所有GPS点数据大致判定各模型的可靠阶次(图 2或图 3),然后确定各简单谱组合模型的组合阶次,再选择一定量的GPS/水准点作为已知点,统计各组合模型的精度,最后对待求GPS点的所有简单谱组合模型结果加权得到该GPS点的全频域高程异常。
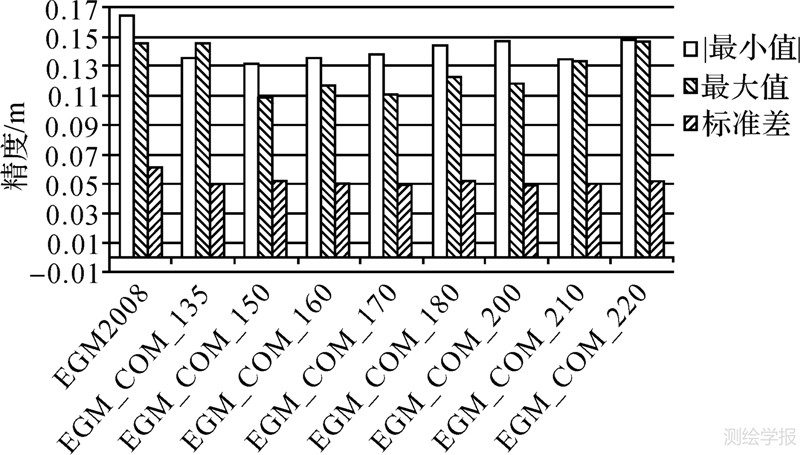
现从每条线路中均匀选择6个GPS/水准点作为已知点,其余406个GPS/水准点作为检核点进行精度评定,已知GPS/水准点平均间距约40 km,利用选择的已知GPS/水准点独立确定每条线路高程系统偏差,并统计各综合模型精度,结果见图 4。图中,最小值为其绝对值,“EGM2008”表示EGM2008模型的精度统计信息,“EGM_COM_135”表示综合模型,即由每个简单谱组合模型(见4.1节)加权求得(见2.3节);每个简单谱组合模型前135阶利用各自模型计算,135阶后利用EGM2008模型补充,其他情况依次类推。另外,综合模型在确保每个简单谱组合模型的中低阶位系数不超出其可靠阶次或最高阶次的前提下,尽可能地利用所有9种模型的信息。图 4结果表明:① EGM2008模型的精度为0.061 m,比表 2中的结果(0.059 m)稍差一些,主要是由于两次计算所采用的已知GPS/水准点数量不同造成的;② 其他8种综合模型的精度介于0.049 m和0.052 m之间,平均精度为0.051 m,比仅利用EGM2008模型精度平均提高了16.4%,无论是“EGM_COM_135”还是“EGM_COM_180”综合模型结果都较为稳定,模型高程异常与实测高程异常的差值均在±15 cm内。
|
| 图 4 综合模型精度统计结果 Fig. 4 The statistic results from combination models |
(1) 数值分析结果表明各地球重力场模型的不同尺度因子ae对模型高程异常计算的影响可以忽略。本文分析的9种地球重力场模型中,AIUB-GRACE03S等8种模型的中低阶位系数(约135阶)整体精度要比同阶次的EGM2008模型高,所有模型精度提高阶次主要集中在100~135阶,部分模型如EIGEN-6C精度提高的阶次更高。
(2) 在CGCS2000大地坐标基准下,通过GPS点的大地坐标以及EGM2008模型或GPS/水准数据可基本确定各模型的可靠阶次。每一种模型(包括组合或综合模型)对应的似大地水准面和我国1985国家高程基准存在系统偏差,且不同区域系统偏差不同,独立确定区域高程系统偏差能提高精度,提高量为7.9%~34.2%。
(3) 简单谱组合方法(组合模型)能充分利用各模型的高精度中低阶位系数,组合模型比EGM2008模型精度提高至少12%。加权谱组合方法(综合模型)能综合利用各类重力场模型信息,求得稳定、高精度的模型高程异常,本文算例得到的高程异常的平均精度为0.051 m,且精度稳定,模型高程异常与实测高程异常的差值均在±15 cm内。值得说明的是,使用该方法时,每个简单谱组合模型对应的高程系统偏差可能不同,加权处理前需要先校正该偏差,加权处理后,也需要利用已知GPS/水准点重新计算该高程系统偏差,从而确定有无必要重新进行系统偏差校正。
(4) 综合各类重力场模型实现区域GPS高程转换具有很好的应用价值,利用少量的GPS/水准点即可获得稳定的、高精度的模型高程异常。本文方法结合GPS测量技术可应用于数字化、信息化成图、土木工程建设等方面,实现低成本、快速高程测量,同时也可用于不稳定地区原有水准点的稳定性检测(如在该区域探测超过15 cm的水准点沉降)。
| [1] | WEI Ziqing ,WANG Gang. Determination of Quasi-geoid Model in Mainland China Using Geopotential and GPS/ Leveling Data[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(1): 1-5. (魏子卿, 王刚. 用地球位模型和GPS/水准数据确定我国大陆似大地水准面[J]. 测绘学报, 2003, 32(1): 1-5.) |
| [2] | WEI Ziqing. GPS Gravity-potential Leveling[J]. Journal of Geodesy and Geodynamics, 2007, 27(4): 1-7. (魏子卿. GPS重力位水准[J]. 大地测量与地球动力学, 2007, 27(4): 1-7.) |
| [3] | HUANG J, VERONNEAU M. Evaluation of the GRACE-based Global Gravity Models in Canada[J]. Newton’s Bulletin, 2009(4): 66-72. |
| [4] | ARABELOS D N, TSCHERNING C C. A Comparison of Recent Earth Gravitational Models with Emphasis on Their Contribution in Refining the Gravity and Geoid at Continental or Regional Scale[J]. Journal of Geodesy, 2010, 84(11): 643-660. |
| [5] | GRUBER T, VISSER P N A M, ACKERMANN C, et al. Validation of GOCE Gravity Field Models by Means of Orbit Residuals and Geoid Comparisons[J]. Journal of Geodesy, 2011, 85(11): 845-860. |
| [6] | HIRT C, GRUBER T, FEATHERSTONE W E. Evaluation of the First GOCE Static Gravity Field Models Using Terrestrial Gravity, Vertical Deflections and EGM2008 Quasigeoid Heights[J]. Journal of Geodesy, 2011, 85(10): 723-740. |
| [7] | PAIL R, BRUINSMA S, MIGLIACCIO F, et al. First GOCE Gravity Field Models Derived by Three Different Approaches[J]. Journal of Geodesy, 2011, 85(11): 819-843. |
| [8] | FöRSTE F, BRUINSMA S, SHAKO R, et al. EIGEN-6-A New Combined Global Gravity Field Model Including GOCE Data from the Collaboration of GFZ-Potsdam and GRGS-Toulouse[R]. EGU General Assembly 2011. Vienna: EGU, 2011. |
| [9] | RIES J C, BETTADPUR S, POOLE S, et al. Mean Background Gravity Fields for GRACE Processing[R]. GRACE Science Team Meeting. Austin: [s.n.], 2011. |
| [10] | GOIGINGER H, HOECK E, RIESER D, et al. The Satellite-only Global Gravity Field Model GOCO02S[R]. General Assembly of the European Geosciences Union. Vienna: European Geosciences Union, 2011. |
| [11] | PAVLIS N K, HOLMES S A, KENYON S C, et al. An Earth Gravitational Model to Degree 2160: EGM2008[R]. Vienna: EGU General Assembly 2008, 2008. |
| [12] | GRUBER T. Evaluation of the EGM2008 Gravity Field by Means of GPS Leveling and Sea Surface Topography Solutions[J]. Newton’s Bulletin, 2009(4): 3-17. |
| [13] | JEKELI C, YANG H J, KWON J H. Evaluation of EGM08-globally and Locally in South Korea[J]. Newton’s Bulletin, 2009(4): 38-49. |
| [14] | CHENG M K, RIES J C, CHAMBERS D P. Evaluation of the EGM2008 Gravity Model[J]. Newton’s Bulletin, 2009(4): 18-25. |
| [15] | FöRSTE C, STUBENVOLL R, KöNIG R, et al. Evaluation of EGM2008 by Comparison with Other Recent Global Gravity Field Models[J]. Newton’s Bulletin, 2009(4): 26-37. |
| [16] | ZHANG Chuanyin, GUO Chunxi, CHEN Junyong, et al. EGM2008 and Its Application Analysis in Chinese Mainland[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 283-289. (章传银, 郭春喜, 陈俊勇, 等. EGM2008地球重力场模型在中国大陆适用性分析[J]. 测绘学报, 2009, 38(4): 283-289.) |
| [17] | ANDERSEN O B. The DTU10 Global Gravity Field and Mean Sea Surface: Improvements in the Arctic[R]. IGFS-2, Fairbanks: Technical University of Denmark, 2010. |
| [18] | HEISKANEN W A, MORITZ H. Physical Geodesy[M]. San Francisco: Freeman W H and Company, 1967. |
| [19] | HIRT C, FEATHERSTONE W E, MARTI U. Combining EGM2008 and SRTM/DTM2006.0 Residual Terrain Model Data to Improve Quasigeoid Computations in Mountainous Areas Devoid of Gravity Data[J]. Journal of Geodesy, 2010, 84(9): 557-567. |
| [20] | ZHANG Xingfu, LIU Cheng. The Approach of GPS Height Transformation Based on EGM2008 and SRTM/DTM2006.0 Residual Terrain Model[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 25-32. (张兴福,刘成. 综合EGM2008模型和SRTM/DTM2006.0剩余地形模型的GPS高程转换方法[J]. 测绘学报, 2012, 41(1): 25-32.) |