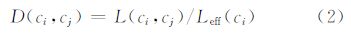2. 武汉大学 遥感信息工程学院,湖北 武汉 430079;
3. 南京师范大学 虚拟地理环境教育部重点实验室,江苏 南京 210046
2. School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, China;
3. Key Laboratory of Virtual Geographic Environment of Ministry of Education, Nanjing Normal University, Nanjing 210046, China
1 引 言
地图综合是一种顾及地图要素地理特征的智能推理行为,尽管最底层的操作是通过坐标点的删除、移动等几何操作过程来实现的,但操作的决策分析是在地理特征层次上产生的[1]。面向地理特征的地图综合,要从空间认识意义上分析出地图要素蕴含的空间知识,是一种结构化的综合行为[2]。在传统地图和地理信息系统的地貌表达中,等高线占有很重要的地位[3],其所蕴含的结构化信息,在地图制图、地貌形态识别、水文分析、DEM建立等领域具有重要的支持作用[4]。
等高线簇的结构化综合实质上是对其所表示的地貌进行结构化综合。地貌的结构化主要包含地性线的提取及组织[5, 6, 7, 8, 9, 10],山脊或山谷的提取[4, 11, 12, 13, 14],汇水区域的划分[15]等方面。现有的研究方法中,利用DEM数据提取地性线及谷地的方法较成熟[5, 6, 7],其应用有文献[11]提出基于次要谷地特征识别与填充的DEM数据结构化综合。近年来基于等高线的地形特征提取及结构化的研究成果不少[8, 9, 10],应用包括文献[12, 13]在曲线弯曲识别的基础上,提取出谷地及河系,并在两者相互约束下实现了基于成组弯曲化简的等高线综合方法;文献[16]利用约束D-TIN构建等高线簇与河网间的空间关系,在两者协同作用下进行综合,有效地避免了要素间的相互冲突;文献[14]利用D-TIN对等高线进行弯曲分析提取出地形特征,实现了等高线与水系数据集成的一致性改正。无论基于谷地还是与水系协同,上述利用等高线对地形进行综合的方法均主要针对地形起伏中的凹陷,但实际情形中,地形起伏中的凹陷与凸起相互依存,综合时,不仅要确定所填充的山谷或洼地,同时还要确定削平的山脊。
本研究在对基于D-TIN的曲线弯曲识别方法改进的基础上,首先识别出单条曲线上的弯曲,再利用等高线的约束D-TIN,提取出成组的弯曲,对等高线中的山谷(或洼地)及山脊进行结构化,作为地貌结构化综合的前提。
2 单条曲线的结构化近年来的研究表明,曲线所蕴含在地理特征上的结构化信息主要通过弯曲特征表现[1, 17, 18]。弯曲识别方法主要分为基于D-TIN的整体识别法[1, 18];基于拐点、极值点等局部特征点的分割法[17, 19]。一方面,受曲线自身形态及曲线上点的分布影响,基于D-TIN的方法存在产生了不符合Gestalt原则的小弯曲[1],弯曲的起始点不为分界点[18],某些弯曲无法识别等问题;另一方面,基于特征点的方法虽然较好地避免了上述问题,但未建立弯曲间的层次及平行关系[18]。因此,结合两种方法的优点识别弯曲,是一种改进其准确率的有效途径。
本研究采取的主要思路是利用D-TIN识别出弯曲并建立其空间关系后,依次进行如下操作:首先结合弯曲间的空间关系判断出伪弯曲并进行合并;然后根据弯曲的骨架特征点[18]以及曲线的形态对弯曲的基点即起始点进行调整;最后删除不符合Gestalt原则的小弯曲并调整弯曲间的空间关系,实现曲线弯曲的结构化表达。
2.1 基于弯曲间空间关系的伪弯曲合并设曲线C由有序点列V={v0,v1,…,vn}组成,任意线段ei满足ei={vi,vi+1}(0≤i≤n-1),则曲线C同时由有序线段列E={e0,e1,…,en-1}组成。
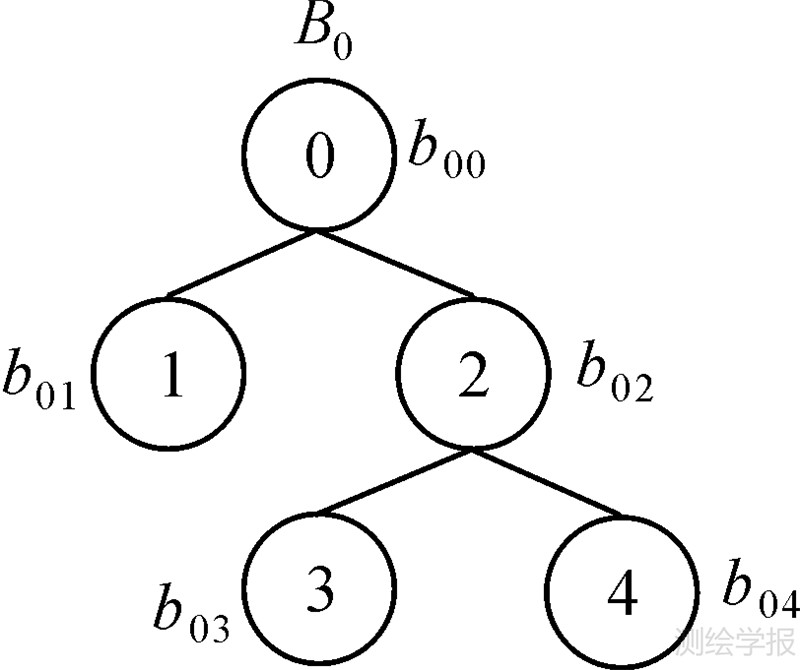
对于曲线C,利用D-TIN建立了m棵相互独立的弯曲层次二叉树C={B0,B1,…,Bm},如图 1所示,其中的一棵树B0,将其中的弯曲按层次优先的顺序表达为B0={b00{b01{b02{b03,b04}}}}。任意弯曲brs满足brs={vi,vi+1,…,vi+j}={ei,ei+1,…,ei+j-1}(0≤i<i+j-1≤n-1),r表示弯曲所在的树编号,s表示弯曲在其所在树中的编号。
|
| 图 1 弯曲层次二叉树 Fig. 1 Hierarchical binary tree of bends |
对于弯曲,有如下概念:
(1) 基点 弯曲起始点与终止点的统称。
(2) 基线 弯曲基点的连线。
(3) 基本弯曲 弯曲层次二叉树中无下级子节点的弯曲。
(4) 复合弯曲 弯曲层次二叉树中包含下级子节点的弯曲。
设bpq、brs为曲线C={v0,v1,…,vn}中的任意两个弯曲,且满足bpq={vi,vi+1,…,vi+j}(0≤i<i+j-1≤n-1),brs={vk,vk+1,…,vk+l}(0≤k<k+l-1≤n-1),则有如下概念:
(1) 异侧相邻弯曲如果(i<k)∧(k<i+j)∧(i+j<k+l)∧(p≠r)则bpq与brs互为异侧相邻弯曲。
(2) 异侧子弯曲如果(i≤k)∧(k+l≤i+j)∧(p≠r)则brs为bpq的异侧子弯曲,也称凹子弯曲。
(3) 同侧子弯曲如果(i≤k)∧(k+l≤i+j)∧(p=r)则brs为bpq的同侧子弯曲,也称凸子弯曲。
(4) 兄弟弯曲如果((i=k+l)∨(i+j=k))∧(bpq与brs具有相同的上一级父弯曲)则bpq与brs互为兄弟弯曲。
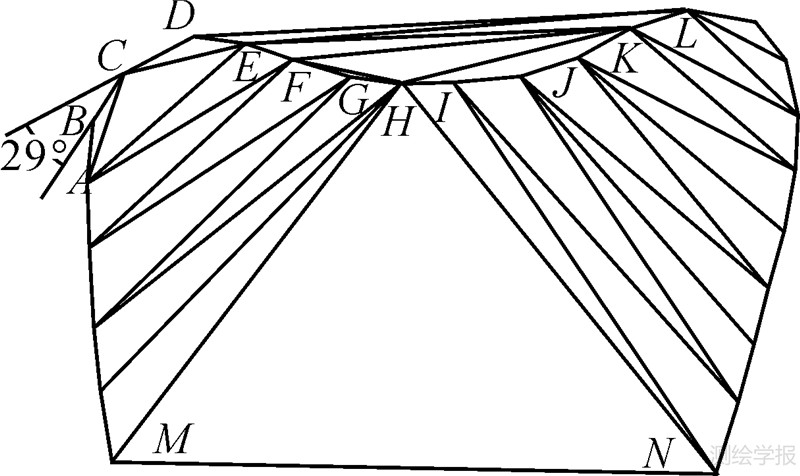
为方便叙述,下文以弯曲的基线表示弯曲,如bvivj指以边vivj为基线的弯曲。文献[1]分析了伪弯曲的形成原因,并给出伪弯曲的判定规则:对于互为兄弟弯曲的两个基本弯曲bpq={vi,vi+1,…,vi+j}及brs={vi+j,vi+j+1,…,vi+j+k},其中(0≤i<i+j-1<ii+j+k-2≤n-2,p=r),若∠vi+j-1vi+jvi+j+1接近180°,则认为该处连续,合并bpq及brs。但这种方法并不严密,它以局部顶角来判断两个基本弯曲是否连续,与局部点分布的关联很强,容易造成误判。如图 2,∠BCD=151°,若bAC与bCE判定为伪弯曲,说明∠BCD接近于180°,但同时,若确定∠GHI接近于180°,应合并bMH及bHN,显然,从整体分析,这两个基本弯曲相互独立,但若确定∠GHI不接近于180°,则bFH及bHK相互独立,这明显不符合视觉感受,因此,无论确定∠GHI是否接近180°,都会产生矛盾。
|
| 图 2 伪弯曲的合并 Fig. 2 Mergence of bogus bends |
针对该问题,本研究提出根据弯曲间的空间关系来判断伪弯曲。连续性是弯曲的一个重要特性,即从曲线的一个方向来看,凹弯曲和凸弯曲交替出现,凹弯曲的相邻弯曲必然是凸弯曲[18]。根据这一特性,对伪弯曲作如下定义:若互为兄弟节点的两个基本弯曲bpq及brs不存在公共的异侧相邻弯曲,则定义bpq及brs为伪弯曲。
伪弯曲合并是将其合并到上一层次的公共父弯曲中使父弯曲成为基本弯曲。对于图 2,依次可以确定,bAC与bCE为伪弯曲,bFH与bHK为伪弯曲。显然本方法从整体上考虑弯曲间的空间关系并确定弯曲是否为伪弯曲,受局部点分布的影响较小。
由有序点列V={v0,v1,…,vn}组成的曲线C,进行约束D-TIN剖分后,对于任意三角形Δ(vi,vj,vk),(i<j<k)可划分为3类[18]:
(1) Ⅰ类三角形 如果(i+1=j)∧(j+1=k),则Δ(vi,vj,vk),为Ⅰ类三角形,记为ΔI(vi,vj,vk)。
(2) Ⅱ类三角形 如果((i+1=j)∨(j+1=k))∧(i+2≠k),则Δ(vi,vj,vk)为Ⅱ类三角形,记为ΔI(vi,vj,vk)。
(3) Ⅲ类三角形 如果(i+1≠j)∧(j+1≠k),则Δ(vi,vj,vk)为Ⅲ类三角形,记为ΔⅢ(vi,vj,vk)。
同时,文献[18]在三角形分类的基础上,给出了如下定义:
(1) 骨架特征点ΔI(vi,vj,vk)中的点vj。
(2) 分叉边ΔⅢ(vi,vj,vk)中的边vivj及vjvk。
文献[18]基于这些定义,根据弯曲间的空间关系,对弯曲的基点进行了调整,包含两种情况:
(1) 如果ΔⅢ(vi,vj,vk)中的点vj不是骨架特征点,则移动vj至bvivj及bvjvk的公共异侧相邻弯曲的骨架特征点处。
(2) 如果(ΔⅢ(vi,vj,vk)中的点vj是骨架特征点)∧(bvivj或bvjvk内存在异侧相邻弯曲的骨架特征点),则移动vi或vk至bvivj或bvjvk对应的异侧相邻弯曲的骨架特征点处。
事实上,文献[18]所提到的两种情况并不完全,例如图 3中的bBD的BC侧相邻弯曲的骨架特征点均未包含在BC之间,因此B点无需调整,但B的位置并不符合视觉感受。本研究对弯曲基点存在的一般形式进行分析并调整。首先明确一点,所有基点的调整均是针对基本弯曲进行操作,复合弯曲基点的调整待基本弯曲调整完后根据基本弯曲的基点进行调整。
|
| 图 3 弯曲基点的类型 Fig. 3 Types of bends’ endpoints |
由弯曲的二叉树结构可知,除树深度为1外(即根节点同时为叶节点),其他情况下,弯曲均成对存在。如图 3所示,某复合弯曲的局部,合并伪弯曲后,bAH包括子弯曲bBF、bFG;bBF包括基本弯曲bBD、bDF;基本弯曲bBD、bDF有公共的相邻弯曲bCE。对于任意基本弯曲bpq={vi,vi+1,…,vi+j},设其兄弟弯曲brs={vi+j,vi+j+1,…,vi+j+k},其中(0≤i<i+j-1<i+j+k-2≤n-2,p=r)。总结起来,基本弯曲的基点可分为以下两类:
(1) 公共点 如果brs为基本弯曲,则点vi+j为公共点。
(2) 自由点 如果brs为基本弯曲,则点vi为自由点;如果(brs为非基本弯曲)∨(brs不存在),则点vi及vi+j均为自由点。
图 3中,点D为公共点,点B及点F为自由点。自由点在不延伸至其他基本弯曲的范围内,或不收缩至自身另一基点的情况下,可自由移动。显然,公共点的调整即为文献[18]所述的第1种情况,而文献[18]的第2种情况则包含在自由点的调整中。
依据公共点及自由点的定义,所有基本弯曲可以分为两类:
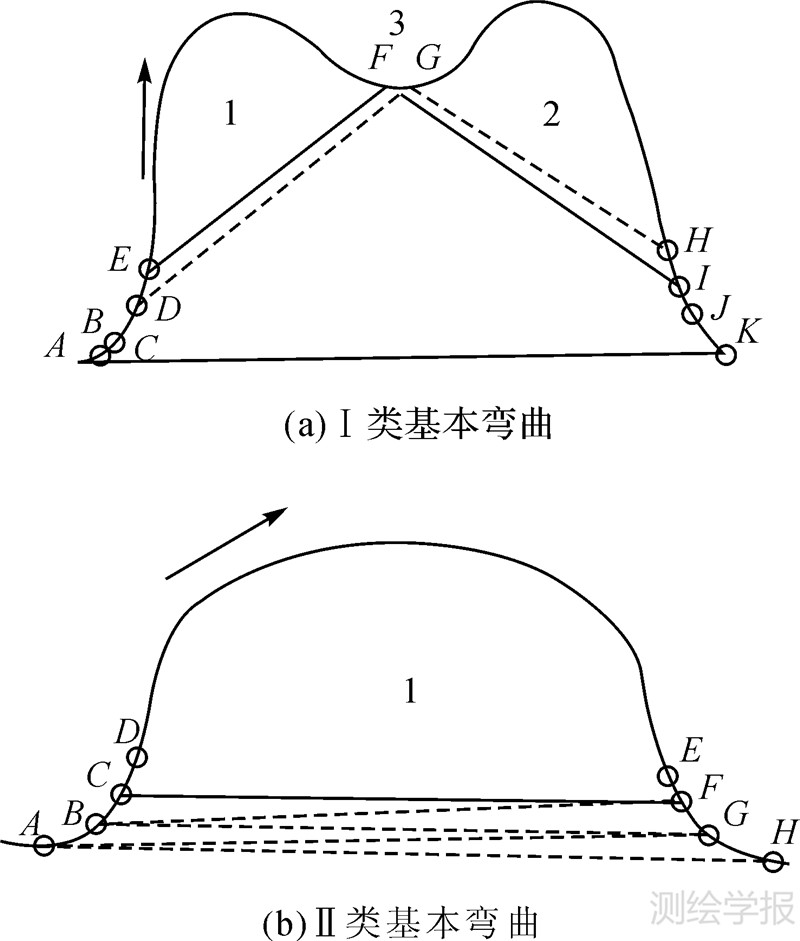
(1) Ⅰ类基本弯曲 两个基点分别为公共点及自由点的基本弯曲。
(2) Ⅱ类基本弯曲 两个基点均为自由点的基本弯曲。
弯曲基点的调整过程,是将当前基点逐点调整至合适的点,使弯曲基本符合视觉感受。首先给出点是否可移动的准则。对于任意基本弯曲brs={vi,vi+1,…,vi+j}(0<i<i+j-1<n-1),定义以下点移动准则:点移动准则,如果vi+j-1与vi+j+1在有向线段e(vi,vi+j)异侧,则点vi+j可延伸至点vi+j+1或收缩至点vi+j-1;同理如果vi+1与vi-1在有向线段e(vi,vi+j)异侧,则点vi可延伸至点vi-1或收缩至点vi+1。
确定这一准则的思想是连续基本弯曲的分界点一般为局部极值点,其切线存在,局部点均在切线一侧。这里,以基线作为近似切线,当前基点作为近似分界点。
对于Ⅰ类基本弯曲bpq={vi,vi+1,…,vi+j},其兄弟弯曲为基本弯曲brs={vi+j,vi+j+1,…,vi+j+k},其中(0≤i<i+j-1<i+j+k-2≤n-2,p=r),基点调整流程为:
(1) 找到bpq及brs的公共异侧相邻基本弯曲的骨架特征点vl。
(2) 若vl=vi+j或vl不存在,则结束。
(3) 逐点向vl移动公共点vi+j,直至不满足点移动准则或移动至点vl,记录移动步距t。
(4) 考虑弯曲的对称性,若bpq公共点向外延伸(向内收缩),则逐点向外延伸(向内收缩)bpq另一侧的自由点,直至不满足点移动准则或移动步距等于t,同理移动brs的自由点。
(5) 结束。
对于Ⅱ类基本弯曲brs={vi,vi+1,…,vi+j}(0<i<i+j-1<n-1),由于受曲线自身形态的影响,识别出来的弯曲往往不符合Gestalt原则,需要将基点向外延伸,其调整流程如下:
(1) 找到brs中vi及vi+j两侧的异侧相邻基本弯曲的骨架特征点vl及vm。
(2) 若vi=vl或vi+j=vm,结束。
(3) 考虑弯曲对称性,交错向外延伸vi及vi+j,每次移动步距为1,直至符合以下条件之一:① 基点调整不满足点移动准则;② vi=vl或vi+j=vm;③ vi或vi+j为其他基本弯曲的基点。
(4) 结束。
如图 4所示的两类基本弯曲的基点调整过程,对于Ⅰ类基本弯曲,按流程依次调整公共点F至G,自由点E及I至点D及H,确定两个基本弯曲为bDG及bGH;对于Ⅱ类基本弯曲,分别逐点调整两个自由点C及F至点A及H,最后弯曲调整为bAH。
|
| 图 4 弯曲基点的调整 Fig. 4 Adjustment of bends’ endpoints |
在弯曲基点调整过程中,之所以较严格地考虑弯曲的对称性,其目的是防止如图 5所示的不符合Gestalt原则的基点调整情况。对图中原始弯曲bAB、bBC的基点进行调整,若不考虑弯曲的对称特性,则最终点A、C将调整至相邻弯曲的骨架特征点M、N,显然,在对曲线进行化简的过程中,针对bAB比针对bMB进行化简更合理(曲线所围面积的改变更小)。因此,在调整基点的过程中,兼顾了弯曲的对称性特征。

|
| 图 5 不符合Gestalt原则的基点调整 Fig. 5 Illegal adjustments of bends’ endpoints |
过于平坦的弯曲不符合视觉感知,综合时,也不能将其视做山谷或山脊,且小弯曲会影响成组弯曲的提取,干扰地形识别。因此,需确定表达弯曲坦陡度的参数来判断是否保留该弯曲。在衡量圆拱的坦陡度时,一般采取矢跨比(又称矢度)来表示,即计算拱圈的矢高与跨径之比,一般矢跨比小于1/5的拱圈称为坦拱,大于或等于1/5的称陡拱。
对于弯曲,矢高定义为骨架特征点到基点所确定直线的距离,跨径定义为两基点之间的距离。但多数情况下,即使是基本弯曲也并不十分对称、平滑,且由于伪弯曲的合并,骨架特征点存在多义性而较难准确确定。因此,计算弯曲的坦陡度时,需要对矢跨比稍做修正,如式
式中,S为弯曲与其基线所围成的面积;L为基线的长度;H为弯曲的矢高,近似为2S/L。
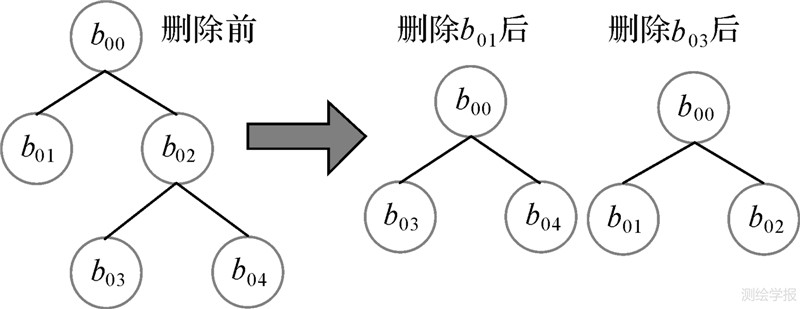
求出所有弯曲的坦陡度后,设定弯曲删除的阈值,将小于该阈值的弯曲删除,其过程如图 6所示,删除b01时,将其与兄弟弯曲b02(复合弯曲)直接合并到父弯曲b00中,并使b02的两个子弯曲成为b00的子弯曲。删除b03时,直接将其与兄弟弯曲b04(基本弯曲)删除。删除小弯曲不改变曲线形态,只影响弯曲识别结果。
|
| 图 6 弯曲的删除过程 Fig. 6 Deletion process of bends |
小弯曲删除后,根据伪弯曲的定义及判断准则对所有基本弯曲进行判断,合并伪弯曲并调整弯曲的基点。重复此过程,直至所有基本弯曲坦陡度均大于删除阈值。弯曲的坦陡度同时也应用到伪弯曲合并时骨架特征点的判定中:两伪弯曲合并后,若其弯曲坦陡度相差较大,则以坦陡度大的弯曲骨架特征点作为合并后新弯曲骨架特征点;当两弯曲坦陡度相差不大时,则以公共点作为新骨架特征点。
3 等高线簇的结构化为了将等高线上识别后的弯曲成组化,需要确定弯曲的类型,即该弯曲表示山脊或是山谷,同时还要确定相邻等高线中的弯曲的邻近关系[20]。为实现这两个目的,首先对等高线进行方向化,使其满足譬如“左高右低”的准则[3],其次,找出衡量等高线之间空间邻近度[20]的参数。现有邻近度表示主要有基于D-TIN及基于Voronoi图两种方法[3, 20]。本研究借助等高线的约束D-TIN来实现,先根据文献[3]所述过程约束的方法,动态插入点生成处处满足Delaunay准则的三角网,并将等高线按“左高右低”准则方向化。
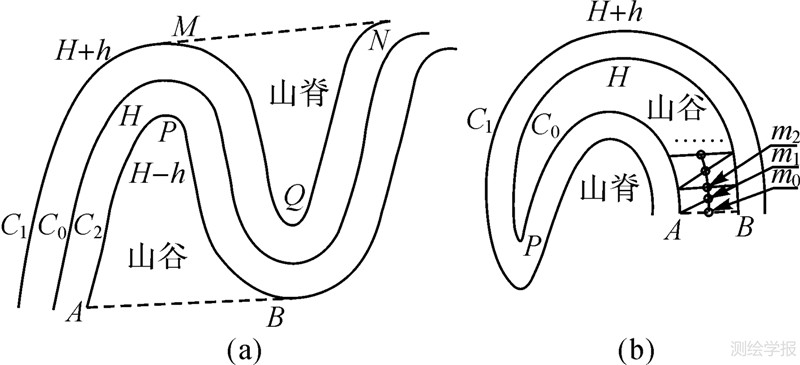
3.1 弯曲类型的确定如图 7所示,曲线C0、C1及C2的高程分别为H、H+h及H-h;bAB的顶点为P;bMN的顶点为Q。
|
| 图 7 基本弯曲类型的确定 Fig. 7 Type determined of elementary bends |
从图 7(a)中基线与顶点之间的关系可以判断:当P在有向线段AB左侧时,该弯曲代表山谷;当Q在有向线段MN右侧时,该弯曲代表山脊。若弯曲的中轴线[21]较平直,利用顶点相对于基线的方向来判断弯曲的类型,所得结果正确,但如图 7(b)所示的弯曲,其中轴线方向变化较大,P在AB右侧,判断该弯曲代表山脊,与实际所示不符,鉴于此,本研究采取根据弯曲中轴线的走势判断弯曲类型。取中轴线与利用弯曲构建的D-TIN中的三角形边的交点依次为{m0,m1,…,mn},其中m0为线段AB中点,mn为顶点P,要确定弯曲的类型,只需判断m1相对于AB的方向,图中m1在AB左侧,则该弯曲代表山谷,与图示一致,或者直接判断A点下一点或B的上一点相对于AB的方向。
3.2 曲线的邻近度文献[3]利用D-TIN对等高线间邻近度的定义为:等高线c1相对于c2的邻近度等于两等高线间第3类边[1]的数量与c1相对于c2的有效点[3]的比值,即D(c1,c2)=Ne12/Nv12,相应D(c2,c1)=Ne12/Nv21,同时记等高线对(c1,c2)的邻近度为=max(D(c1,c2),D(c2,c1))。由定义可得出该邻近度并不归一化,不同等高线对之间的邻近度无法比较。
文献[20]利用Voronoi图得出邻近系数的概念:等高线的Voronoi图中,相邻等高线的邻接系数是Voronoi公共边的总长度与两个Voronoi多边形之较小周长之比,即邻接系数=∑Voronoi公共边长度/min(左、右Voronoi多边形周长)。该邻接系数的取值范围为[0,1],其值越小,邻接程度越低。
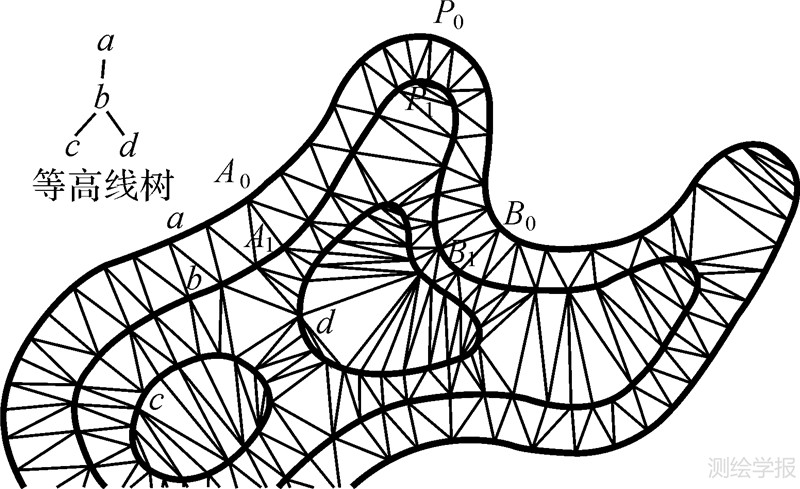
本研究中,实际要求得的邻近度为弯曲间的邻近度,即等高线簇中任意曲线段间的邻近度。如图 8所示的等高线示意图及其对应的树结构。定义等高线ci相对于cj的邻近度为
式中,L(ci,cj)为在等高线ci上且与cj之间有三角形相连的线段的总长度;Leff(ci)为等高线的有效长度,即除去那些与自身有三角形相连的部分的长度。有效长度提出的基础是:在构建等高线的Voronoi图时,等高线间Voronoi图的公共边穿过那些与有效部分相连的三角形。
|
| 图 8 曲线邻近度计算 Fig. 8 Calculation of curve proximity |
由定义可知,该邻近度具有以下性质:
(1) D(ci,cj)的取值范围为[0,1]。
(2) D(ci,cj)不一定等于D(cj,ci)。
(3) 设{cj,cj+1,…,cj+n}为所有与ci邻近且在ci同侧的等高线集合,则有 (ci,ck)=1 。
(ci,ck)=1 。
根据等高线间邻近度的定义,能求得等高线中所包含的任意一段弯曲与其他弯曲的邻近度,例如图中等高线a上弯曲bA0,B0(记为b0),与等高线b上的弯曲bA1,B1(记为b1)之间的邻近度有D(b0,b1)=D(b1,b0)=1。
3.3 成组弯曲的提取成组弯曲提取的关键是找出每个弯曲在相差一个高差的等高线上的邻近弯曲,并根据邻近关系顺次查找出地形结构中的山谷或山脊。当比例尺变小时,地形细节需简化,最直接的影响是基本弯曲所表达的简单地形的简化,若比例尺进一步缩小,原本的复合弯曲由于子弯曲的删除变为基本弯曲,此时,再重新建立基本弯曲间的邻近关系。因此,这里仅以基本弯曲为对象查找邻近弯曲。
以查找高一个高差的邻近弯曲为例,设基本弯曲brs={vi,vi+1,…,vi+j}(0<i<i+j-1<n-1),其高程为H,等高线间高差为h,邻近弯曲的查找过程分两步。
(1) 找出所有与brs邻近且类型相同高程为H+h的基本弯曲集B={b1,b2,…,bm}:① 初始化k=i;② 若k=m,结束;③ 获取约束边e(vk,vk+1)所关联的三角形,找出除约束边端点外且高程为H+h的第3点vp;④ 若vp为空,令k=k+1,转②;⑤ 获取vp的下一点vp+1,若vp+1为空,令k=k+1,转②;⑥ 找到与边e(vp,vp+1)关联的基本弯曲,若类型与brs相同,加入到弯曲集B中,令k=k+1,转②。
(2) 从弯曲集B中筛选出邻近的弯曲:① 依次计算brs与B中弯曲的邻近度Dl=D(brs,bl)(l=0,1,…,m),若Dl≥d(d为阈值,例如取0.7),则返回该弯曲,即找到高一个高差的邻近基本弯曲;② 若无法找到满足阈值要求的邻近基本弯曲,则依次计算D′l=D(bl,brs)(l=0,1,…,m),返回所有D′l≥d的弯曲。
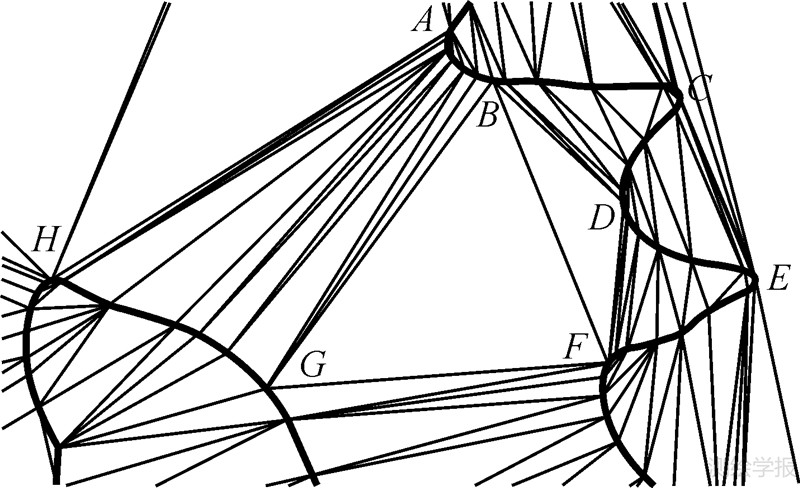
如图 9所示,查找到bAB的邻近弯曲集为{bCD,bDE},但D(bAB,bCD)及D(bAB,bDE)的值均很小。因此,计算D(bCD,bAB)及D(bDE,bAB)的值,最终查找到bAB的邻近弯曲为bCD及bDE,这刚好对应地性线的树形结构,图中为河流的分支结构。

|
| 图 9 成组弯曲提取 Fig. 9 Extraction of bends set |
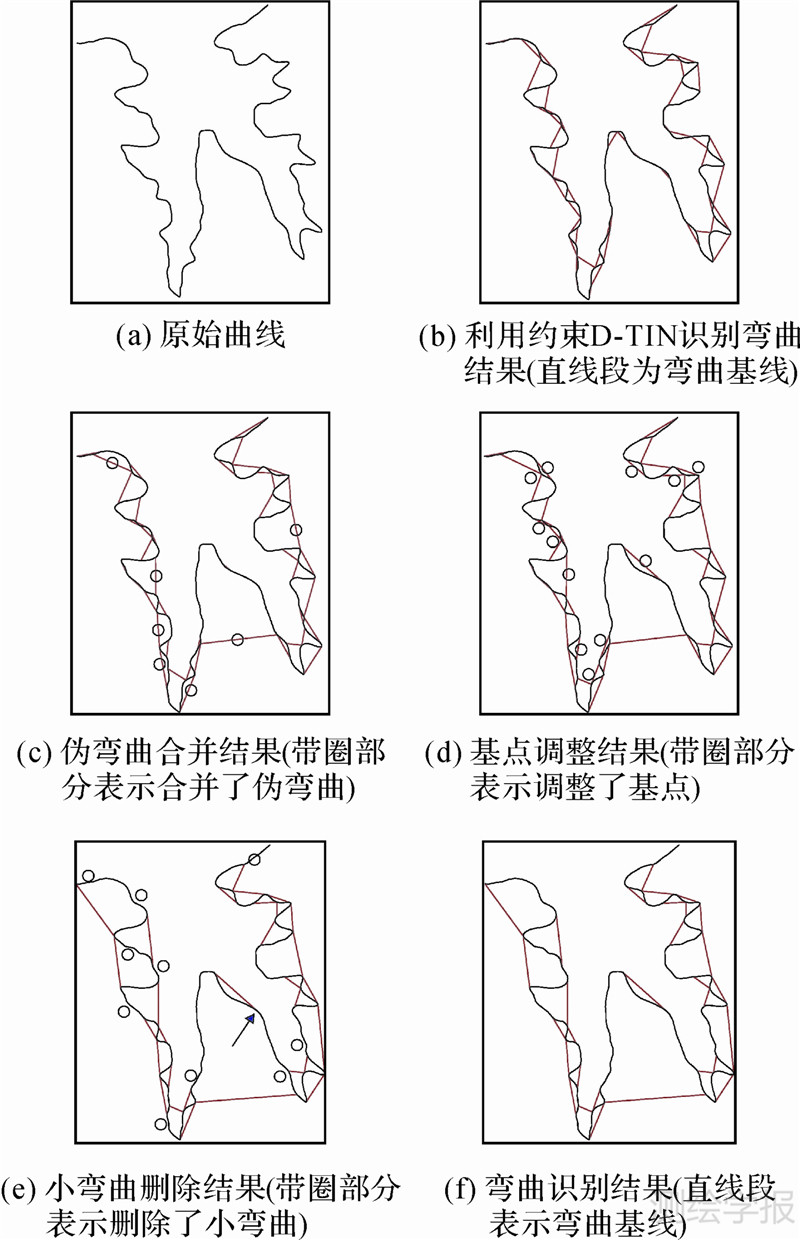
首先验证曲线弯曲识别的方法,如图 10(a)所示的原始曲线,按文中所述流程识别出弯曲,结果如图 10(f)所示,其中,取弯曲坦陡度的阈值为1/6。图 10(e)中箭头所指之处的弯曲并未正确识别,其原因是基于D-TIN的弯曲识别受曲线自身形态的影响。从最终结果看,弯曲识别基本合理。
|
| 图 10 曲线弯曲识别过程图 Fig. 10 Process of curve bends recognition |
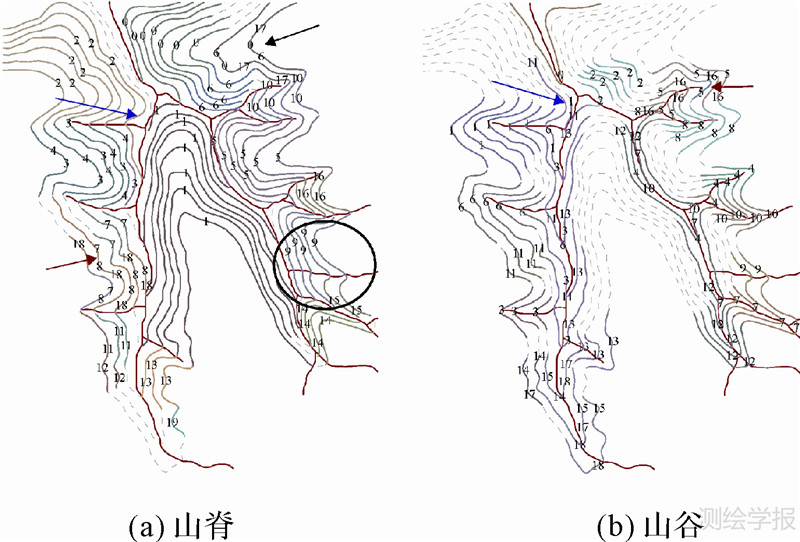
在曲线弯曲识别的基础上,按上文所述方法,对图 11所示的等高线簇进行结构化,取弯曲的邻近度阈值为0.7,提取出成组的弯曲。图中利用不同的颜色表示不同组的弯曲,数字标号表示弯曲的组号,有多个标号的弯曲(如图 11(a)中黑色箭头所指部分)表示对应地形上的分叉结构。从等高线与河流的叠加来看,山脊部分在河流分支之间,山谷部分与河流重合,结果基本合理。
|
| 图 11 等高线簇结构化 Fig. 11 Structuralization of contour cluster |
在提取成组弯曲的过程中,参考两个相邻弯曲bpq及brs之间的邻近度D(bpq,brs)及D(brs,bpq)来判断两者是否表达同一山谷或山脊,邻近度阈值的取值对计算结果影响不大,图 11(a)山脊识别结果中,仅当邻近度阈值取0.5时,圆圈标记处所示结果与取值大于0.5时的结果有所不同,而其他的山脊与山谷识别结果在不同取值时均一致。为防止邻近度较小的两个弯曲被认为表达同一山脊或山谷,本例中取阈值为0.7。
在图 11(a)中,红色箭头所指之处并不十分合理,其原因是相邻等高线之间具有一定的相似性,使得其弯曲分布保持一定的相关性,但本文基于单条等高线的弯曲识别暂未考虑这种相关性,图 11(b)红色箭头亦如是。两幅子图蓝色箭头所指部分的弯曲识别结果同样不甚合理,其原因是受曲线自身形态影响,箭头所指之处弯曲未被识别。从图中可以看出,所识别的弯曲组中(例如图(a)中弯曲组2、5)存在着小起伏,这是在弯曲识别过程中删除了小弯曲所引起的结果,其目的是识别出地形整体结构中的大起伏,反映分水线、集水线等决定性因素对地形的影响作用,而将小起伏视作大起伏中的随机噪声,反映其他因素对地形的局部影响。相应的,在基于弯曲的地形综合过程中,可以采取两步走的综合策略,即先对成组弯曲中小的起伏进行光滑,再确定成组弯曲的取舍,来体现小弯曲与大弯曲在地形综合中各自的作用。
5 结 论本研究对基于D-TIN的曲线弯曲识别方法进行了改进,并利用等高线簇的约束D-TIN,提取出等高线簇中的成组弯曲。试验表明,曲线弯曲识别及等高线簇成组弯曲的提取方法是合理有效的。
根据试验过程及结果,基于弯曲识别的等高线簇结构化方法中需要进一步研究的内容包含:① 消除曲线自身形态对弯曲识别结果的影响;② 考虑相邻等高线之间的相关性以改进弯曲的识别结果;③ 对封闭曲线进行结构化并将其应用到成组弯曲的提取中;④ 提取成组弯曲时,考虑复合弯曲其他弯曲之间的邻近关系,建立完整的地形结构间的空间关系。最后,在解决上述问题的基础上,实现基于地形结构识别的地形多尺度表达。
| [1] | AI Tinghua, GUO Renzhong, LIU Yaolin. A Binary Tree Representation of Curve Hierarchical Structure in Depth[J]. Acta Geodaetica et Cartographica Sinica, 2001,30(4):343-348.(艾廷华, 郭仁忠, 刘耀林. 曲线弯曲深度层次结构的二叉树表达[J]. 测绘学报, 2001,30(4):343-348.) |
| [2] | WU Hehai. Structured Approach to Implementing Automatic Cartographic Generalization [C]// Proceedings of the 18th ICC. Stockholm:[s.n.], 1997. |
| [3] | WANG Tao, WU Hehai. Construction and Applications of Topological Relation among Contour Lines[J]. Geomatics and Information Science of Wuhan University, 2004,29(5):438-442.(王涛, 毋河海. 等高线拓扑关系的构建以及应用[J]. 武汉大学学报:信息科学版, 2004,29(5):438-442.) |
| [4] | AI Tinghua, ZHU Guorui, ZHANG Genshou. Extraction of Landform Features and Organization of Valley Tree Structure Based on Delaunay Triangulation Model[J]. Journal of Remote Sensing, 2003,7(4):292-298.(艾廷华, 祝国瑞, 张根寿. 基于Delaunay三角网模型的等高线地形特征提取及谷地树结构化组织[J]. 遥感学报, 2003,7(4):292-298.) |
| [5] | LIU Xuejun, WANG Yongjun, GONG Jianya, et al. Error Analysis of Drainage Network Algorithms Based on Digital Elevation Model(DEM)[J]. Acta Geodaetica et Cartographica Sinica,2007,36(2):224-230.(刘学军, 王永君, 龚健雅, 等. DEM流域网络提取算法的误差特性分析[J]. 测绘学报, 2007,36(2):224-230.) |
| [6] | YANG Zuqiao, GUO Qingsheng, NIU Jiping, et al. A Study on Multi-scale DEM Representation and Topographic Feature Line Extraction[J]. Acta Geodaetica et Cartographica Sinica,2005,34(2):134-137.(杨族桥, 郭庆胜, 牛冀平, 等. DEM多尺度表达与地形结构线提取研究[J]. 测绘学报, 2005,34(2):134-137.) |
| [7] | HUANG Peizhi, LIU Zehui. Extraction of Ridge and Valley from DEM Based on Gradient[J].Geomatics and Information Science of Wuhan University,2005,30(5):396-399.(黄培之, 刘泽慧. 基于地形梯度方向的山脊线和山谷线的提取[J]. 武汉大学学报:信息科学版, 2005,30(5):396-399.) |
| [8] | GUO Qingsheng, YANG Zuqiao, FENG Ke. Extracting Topographic Characteristic Line from Contours[J]. Geomatics and Information Science of Wuhan University, 2008,33(3):253-256, 304.(郭庆胜, 杨族桥, 冯科. 基于等高线提取地形特征线的研究[J]. 武汉大学学报:信息科学版, 2008,33(3):253-256, 304.) |
| [9] | WU Fan, SU Weimin, YANG Yingwei, et al. Extracting Terrain Features from Contour Maps Based on United-Delaunay-Triangulation Model[J]. Journal of China University of Mining & Technology, 2007,36(2):172-176.(吴凡, 粟卫民, 杨英伟, 等. 基于联合Delaunay三角网的等高线地形特征提取研究[J]. 中国矿业大学学报, 2007,36(2):172-176.) |
| [10] | JIN Hailiang, KANG Jianrong, GAO Jingxiang. Research on the Algorithm of Extracting Ridge and Valley Lines Using Contour Data[J]. Geomatics and Information Science of Wuhan University,2005,30(9):809-812.(靳海亮, 康建荣, 高井祥. 利用等高线数据提取山脊(谷)线算法研究[J]. 武汉大学学报:信息科学版, 2005,30(9):809-812.) |
| [11] | AI Tinghua, LI Jingzhong. A DEM Generalization by Minor Valley Branch Detection and Grid Filling[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2010,65(2):198-207. |
| [12] | AI Tinghua. The Drainage Network Extraction from Contour Lines for Contour Line Generalization[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2007,62(2):93-103. |
| [13] | AI Tinghua. A Generalization of Contour Line Based on the Extraction and Analysis of Drainage System [C]// Proceedings of 20th ISPRS Congress.Istanbul:[s.n.], 2004. |
| [14] | YANG Min, AI Tinghua, LIU Pengcheng, et al. The Matching and Consistency Correcting in the Integration of Contour and River Network[J]. Acta Geodaetica et Cartographica Sinica,2012,41(1):152-158.(杨敏, 艾廷华, 刘鹏程, 等. 等高线与水网数据集成中的匹配及一致性改正[J]. 测绘学报, 2012,41(1):152-158.) |
| [15] | ZHU Qing, TIAN Yixiang, ZHANG Yeting. The Extraction of Catchment and Subcatchment from Regular Grid DEMs[J]. Acta Geodaetica et Cartographica Sinica, 2005,34(2):129-133.(朱庆, 田一翔, 张叶廷. 从规则格网DEM自动提取汇水区域及其子区域的方法[J]. 测绘学报, 2005,34(2):129-133.) |
| [16] | LONG Yi, CAO Yang, SHEN Jie, et al. Cooperative Generalization Method of Contour Cluster and River Network Based on Constrained D-TIN[J]. Acta Geodaetica et Cartographica Sinica,2011,40(3): 379-385.(龙毅, 曹阳, 沈婕, 等. 基于约束D-TIN的等高线簇与河网协同综合方法[J]. 测绘学报, 2011,40(3):379-385.) |
| [17] | QIAN Haizhong, WU Fang, CHEN Bo, et al. Simplifying Line with Oblique Dividing Curve Method[J]. Acta Geodaetica et Cartographica Sinica,2007,36(4):443-449, 456.(钱海忠, 武芳, 陈波, 等. 采用斜拉式弯曲划分的曲线化简方法[J]. 测绘学报, 2007,36(4):443-449, 456.) |
| [18] | ZHAI Renjian, WU Fang, ZHU Li, et al. Structured Representation of Curve Shape[J]. Acta Geodaetica et Cartographica Sinica,2009,38(2):175-182.(翟仁健, 武芳, 朱丽, 等. 曲线形态的结构化表达[J]. 测绘学报, 2009,38(2):175-182.) |
| [19] | GUO Qingsheng, HUANG Yuanlin, ZHANG Liping. The Method of Curve Bend Recognition[J]. Geomatics and Information Science of Wuhan University, 2008,33(6):596-599.(郭庆胜, 黄远林, 章莉萍. 曲线的弯曲识别方法研究[J]. 武汉大学学报:信息科学版, 2008,33(6):596-599.) |
| [20] | LIU Jianjun, CHEN Jun, WANG Donghua, et al. The Study of Description and Application of Contour Adjacency Relationship[J]. Acta Geodaetica et Cartographica Sinica,2004,33(2):174-178.(刘建军, 陈军, 王东华, 等. 等高线邻接关系的表达及应用研究[J]. 测绘学报, 2004,33(2):174-178.) |
| [21] | WU Hehai. Automatic Generalization of Relief Form[J]. Geomatics and Information Science of Wuhan University, 1995,20(S1):1-6.(毋河海. 地貌形态的自动综合问题[J]. 武汉测绘科技大学学报, 1995,20(S1):1-6.) |