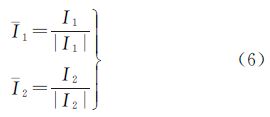
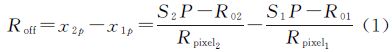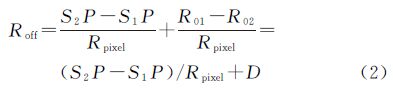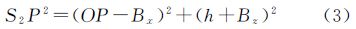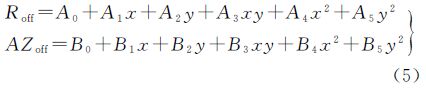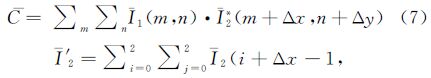2. 中国测绘科学研究院,北京 100830
2. Chinese Academy of Surveying and Mapping,Beijing 100830,China
1 引 言
机载重复轨道干涉合成孔径雷达(synthetic aperture radar,SAR)数据的配准精度直接影响后续的数据处理。由于每一次获取数据时的飞行速度、方向、姿态都不完全相同,因此影像对之间产生平移、缩放、旋转、甚至不规则的局部变形。影像间较大的相对变形使得现有算法很难满足整幅影像的高精度配准。
目前广泛应用的配准方法有:相关函数方法[1]、频谱极大值法[2]、平均波动函数法[3]及其改进算法[4, 5, 6, 7]。这些配准方法都是在主影像上等间隔选取一定数量的点,对副影像过采样并以一定的配准测度函数为评价标准获取所选点的偏移量,用多项式拟合出整幅影像的偏移量,从而完成干涉影像对的配准。这些方法存在的问题有:① 选点时没有考虑有效性,搜索窗口大小难以选择,对误匹配的检测不够。对于机载数据而言,近距和远距的变化较大,且存在一定的局部变形,搜索窗口设置过小,窗口内没有同名点,造成误匹配,窗口过大,窗口内可能存在多个极值点,同样会产生误匹配,且计算量较大。在完成匹配点对的计算之后,仅剔除信噪比较低的点,并不能完全消除错误匹配的点;② 使用多项式拟合引入了新的误差,对于星载重轨和机载双天线的干涉数据而言,对多项式拟合后的残差值很小,可以忽略,但是对机载重复轨道数据而言,多项式拟合后的残差值可以达到数个像元,因此必须采取一定的措施消除影响。因此,对于机载重复轨道干涉数据,传统方法获取的结果:有效匹配点数少、误匹配多、多项式拟合后残差值较大、无法满足机载重轨干涉SAR要求的配准精度。
近些年,一些新的配准算法被提出。文献[8, 9, 10]提出的SIFT 算法具有尺度不变、稳健的特性,得到了广泛的关注[11, 12, 13]。文献[14]将SIFT算法引入全极化数据的配准处理中,对全功率图(total power image)使用SIFT方法进行配准。文献[15]讨论了在DEM辅助下的配准结果的改善情况,利用大量不同空间基线的COSMO-SkyMed和TerraSAR-X数据进行试验,得出在地形起伏较大的区域空间基线越长改善效果越明显的结论。文献[16, 17]提出解析搜索的方法,可以在精度达到1个像元的粗配准基础上,逐点计算精确匹配值,较好地解决局部相对变形。文献[18, 19]在传统配准方法的基础上增加奇异点(singular points,SPs)的数目作为评价标准,并引入SFS(shape-from-shading)技术提高信噪比。文献[20]将SAR影像看做分形布朗运动模型(fractional Brownian motion,fBm),将配准过程等价为求解两个fBm信号的偏移量。
本文结合SIFT匹配算法和解析搜索算法的技术特点,对SIFT算法加以改进作为粗配准,以解析搜索算法为精配准,提出了一种针对机载重复轨道干涉SAR数据的配准方法,以解决机载重复轨道干涉SAR的配准问题。并采用国产CASMSAR系统获取的P波段重复轨道干涉数据进行配准试验,获取了清晰的干涉条纹图。
2 针对机载重复轨道干涉SAR数据的配准方法针对机载重复轨道干涉SAR数据的特点,本文结合SIFT算法比较稳健的特性和解析搜索算法精度高的优势,提出了一种针对机载重轨干涉SAR的配准算法。算法分为两步:基于改进的SIFT算法的粗配准和基于解析搜索算法的精配准。整个算法流程如图 1所示。
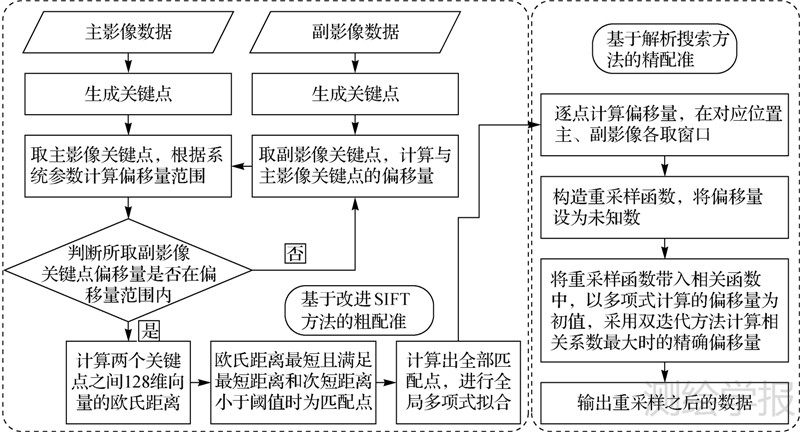
|
| 图 1 算法流程示意图 Fig. 1 Algorithm flowchart |
SIFT算法可以提取大量有效的特征点,且近似均匀分布,因此选用SIFT方法提取特征点。但是,两幅影像间的特征点进行匹配时,由于是对整景影像的特征点进行搜索,不但效率低下且误匹配严重。考虑到轨道数据与影像间偏移量存在一定关系,可以通过轨道参数计算出影像间的偏移量范围。在特征点匹配时,首先判断特征点偏移量是否在偏移量区间范围内,若在范围内则计算其欧氏距离,若不在范围内则跳过,最后认为欧式距离最短且满足一定约束的点对为匹配点。这样既避免了对每一点都计算距离,降低了计算量和误匹配,由此完成粗配准。
SIFT匹配后进行多项式拟合,残差值虽然较其他方法小,但仍有1~3个像元,远大于干涉要求的1/8像元的精度。这是由较大的相对变形造成的,影像间的相对变形不能完全由多项式描述。若要获得较高的配准精度,必须逐点进行配准。如果使用传统的配准方法进行逐点的搜索,由于需要过采样和在窗口内进行全面的搜索,计算量十分巨大,且精度与过采样系数相关,因此需要一种既能够保证精度并且计算量适中的算法。解析搜索的方法具有配准精度高、适用于较大变形、计算量适中的特点,符合逐点计算的要求。解析搜索方法的主要思想是:将包含未知偏移量的重采样函数代入相关函数中,通过数学方法求解相关函数最大值,实现了在连续域内的搜索,使配准精度在插值意义上达到最优。
3 基于改进SIFT算法的粗配准SIFT算法在尺度空间寻找并描述关键点,并对影像间的关键点进行匹配。算法分为3步:生成尺度空间、检测并描述关键点、关键点匹配。
(1) 高斯卷积核是实现尺度变换的唯一线性变换核[21],通过影像与具有可变核的高斯滤波器进行卷积,建立高斯金字塔LoG(Laplacian of Gaussian),再利用DoG(difference of Gaussian)算子形成高斯差分尺度空间。
(2) 寻找在尺度空间为极值的点作为关键点,确定关键点的主方向和梯度幅值,在关键点的邻域内统计梯度直方图,并计算特征向量。关键点即为特征点,由影像坐标、主方向、梯度幅值和特征向量描述。
(3) 取主、副影像关键点,计算特征向量间的欧氏距离d|Vm-Vs|作为相似程度的判断标准,为了减少误匹配,取最短距离d1与次短距离d2的比值小于某一阈值时,认为距离最短的两个关键点是匹配点[11]。当阈值取0.8时,损失了5%的正确匹配点,同时也减少了90%的错误匹配点[11]。
实际试验发现,按照上述方法匹配,对主影像上每一个关键点,都与副影像上所有点计算欧氏距离,计算量十分巨大,结果也不理想,存在大量明显的误匹配,多项式拟合后的残差值高达数百像元。
由于干涉数据的特殊性,可由系统参数和轨道数据计算出影像偏移量的分布区间。如图 2所示,X轴为距离向;Z轴为天顶方向;S1、S2分别为天线1和天线2的位置;h为天线1的相对高程;Bx、Bz分别是基线在X、Z轴的投影;P点为地面点,其在主副影像上的影像坐标分别为(x1p,y1p)、(x2p,y2p),其中,x为距离向;y为方位向。
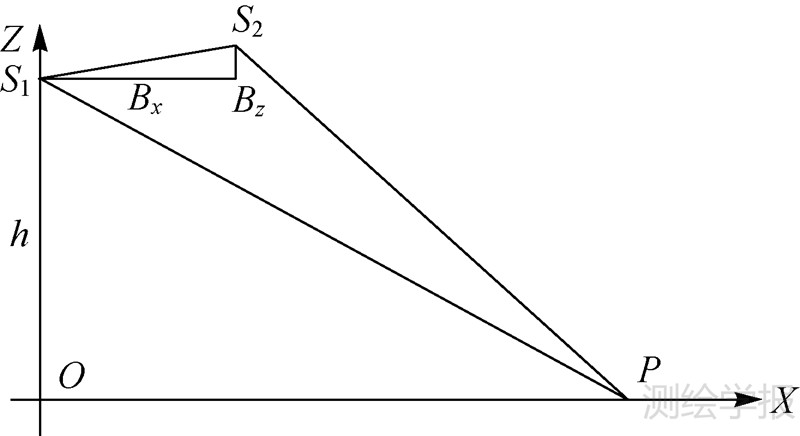
|
| 图 2 基于基线计算距离向偏移量示意图 Fig. 2 Calculation offset in range direction based on the baseline |
考虑距离向上的影像坐标关系,x2p=x1p+Roff,可得距离向上的偏移量为
式中,S1P和S2P分别为天线1和天线2到目标点P的距离;R01和R02分别为主影像和副影像的初始斜距;Rpixel1和Rpixel2分别为主影像和副影像距离向上的采样间隔。一般而言,Rpixel1=Rpixel2=Rpixel,式(1)可简化为 式(2)中,D=(R01-R02)/Rpixel。为了便于计算,取平地模型 将式(3)代入式(2),距离向偏移量公式可以写为 式(4)中的未知参数为目标点P的斜距S1P,将主影像的近距端斜距和远距端斜距分别代入式(4),可计算出距离向上偏移量的最小值和最大值。考虑到采用平地模型、轨道不平行误差、地形变化、影像内部变形等诸多因素的影响,实际应用时应对区间扩大5~10个像元。在上述步骤(3)计算欧氏距离之前,首先判断这两个关键点之间的偏移量是否在偏移量区间范围内,若不在范围内,则不必计算欧氏距离。仅考虑距离向上偏移量已经能够大大降低运算量,满足配准要求,因此本文没有考虑方位向上的偏移量。在获取匹配点后,按照式(5)进行多项式拟合,并剔除残差值较大的点
4 基于解析搜索的精配准由于SIFT算法的精度仅有1~3个像元,而解析搜索算法需要首先达到像元级的精度,因此需要增加一步,使配准精度优于一个像元。本文采用相关函数法,对主影像上每一点,通过多项式计算到副影像上对应点,以残差值的最大值为搜索窗口的半径进行搜索,使配准精度达到解析搜索算法的要求。
在精配准时,为避免幅度的影响,需要对幅度进行归一化处理;同时考虑到计算的可行性,用二次B样条函数[22]代替理想的sinc函数作为重采样的权函数。
精配准的处理步骤如下:
(1) 将主、副影像进行归一化处理
(2) 在SIFT匹配的基础上,采用相关函数法,使配准精度优于一个像元。
(3) 构造相关函数,将包含未知偏移量的重采样函数带入相关函数内
式中,I′2为重采样后副影像的值;Fx,2为距离向的权函数;Fy,2为方位向的权函数;重采样窗口大小为3像元×3像元。(4) 对方位向和距离向的偏移量求偏导函数,并令为0,假定二者是可分离的,采用双迭代的方法交替求解方位向和距离向的偏移量
每一个偏导函数都是一个一元三次方程,利用盛金公式[23]求解三次方程,避免了文献[17]中在求解方程时利用弦割法迭代求解,降低了运算量。(5)输出偏移量和重采样后的数据。
(6)对每一个点重复(2)—(5)步,完成精配准。为了减小计算量,相邻像元使用上一像元的偏移量计算结果作为初值进行迭代计算。
5 试验分析CASMSAR是中国测绘科学研究院联合多家单位研制的机载SAR系统,安装有X波段HH极化双天线和P波段全极化单天线系统。本次试验采用2011-06-23两次飞临河南登封地区的P波段数据,其飞行航线间隔约56 m。
影像参数见表 1。
| 主副影像相同的参数 | |||
| 波长/m | 0.5 | PRF/Hz | 800 |
| 极化方式 | VV | 影像时间间隔/min | 约25 |
| 方位向采样点数 | 8192 | 基线水平分量/m | 约54.9 |
| 距离向采样点数 | 6144 | 基线竖直分量/m | 约7 .6 |
| 主副影像不同的参数 | |||||
| 参数 | 主影像 | 副影像 | 参数 | 主影像 | 副影像 |
| 飞行高度/m | 3152 | 3150 | 飞行速度/(m/s) | 120.8 | 120.7 |
| 场景中心视角/(°) | 60.09 | 60.15 | 方位向间隔/m | 0.604 | 0.603 |
| 多普勒中心频率/Hz | -34.2 | -25.6 | 距离向间隔/m | 0.625 | 0.625 |
分别使用相关函数法、频谱极大值法、SIFT算法和本文提出的方法对上述影像进行粗配准。提取一定数目的匹配点,利用最小二乘方法,按照式(4)形式拟合多项式系数。令A=[a0 a1 a2 a3 a4 a5],B=[b0 b1 b2 b3 b4 b5]分别为距离向和方位向上多项式拟合系数。由相关函数法求得的多项式系数为
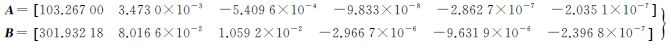
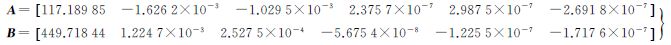


各方法拟合多项式后的残差值如表 2所示。
| 配准方法 | 相关函数法 | 频谱极大值法 | SFIT方法 | 本文方法 |
| 距离向残差 | 0.27 | 4.22 | 549.699 1 | 0.60 |
| 方位向残差 | 23.79 | 5.01 | 741.736 5 | 0.99 |
| 匹配点数 | 3155 | 433 | 2025 | 7484 |
各方法拟合多项式后的残差值直方图如图 3所示。
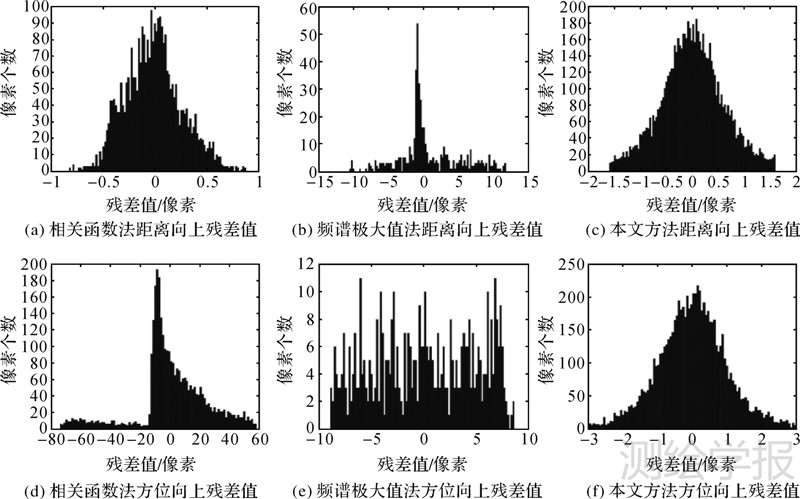
|
| 图 3 残差值统计 Fig. 3 Statistics of residuals |
按照计算出的多项式系数对辅影像进行重采样,重采样结果如图 4所示。

|
| 图 4 原始主影像与重采样后的辅影像 Fig. 4 Original master image and resampled slave images |
图 3是各方法的残差值统计直方图,图 4为主影像和通过各方法配准后重采样的副影像,其中图 4(a)—(d)是整幅影像,图 4(e)—(h)为对应的左上角局部图。由多项式系数和表 2的残差值可以看出,SIFT算法存在大量误匹配,拟合出的多项式错误明显,因此在图 3、图 4中没有将SIFT算法与其他方法作比较。
虽然相关函数法和频谱极大值法原本是精配准的方法,但是由于机载重复轨道数据相对变形比较大,这两种方法没有达到干涉所需的精度。因此在本试验中,将这两种方法与粗配准的方法作比较。在距离向和方位向分别均匀选取60个和80个采样点,理想情况下会计算出4800个精确匹配点。
相关函数方法提取出3155个有效匹配点。从残差值的统计来看,在距离向上具有较高的精度,而方位向上的残差值很大,达到了23.79个像元。这是由于受到轨道不平行和飞行速度不一致的影响,影像在方位向上相对变化较大,从而导致相关函数方法在方位向上获取了相当数量的错误匹配点。
最大频谱法有效匹配点数比较少,仅匹配433个点,且残差值比较大,在方位向和距离向分别达到了5像元和4.22像元。从直方图分配来看,方位向上残差值分布比较均匀,方位向上的匹配精度略低于距离向。
SFIT方法可以选取相当数量的匹配点,但是其中一部分存在明显错误。由于在匹配过程中进行全局的搜索,误匹配点没有规律,而且偏移量很大,与正常值的差异可以达到数千像元。大量误匹配点的存在,使得计算得出的多项式系数明显是错误的,残差值也很大。
本文提出的方法,在计算欧式距离之前,先利用式(4)进行判断,当两关键点满足条件时,计算欧式距离,否则认为两点不是同名点,不计算欧氏距离。该方法大大降低了匹配过程中的运算量,同时提高了有效匹配点数,残差值比较小。该方法也存在方位向残差值大于距离向残差值的现象。
距离向上偏移量的分布,对配准结果进行统计,相关函数法为[86.99,113.98],频谱极大值法为[88.76,123.67],SIFT算法为[-2 430.31,2 514.38],本文方法为[92.33,113.66],通过式(4)计算得出的区间为[78.73,113.69]。可见通过式(4)计算得出的距离向上偏移量的分布区间与实际情况比较吻合,而SIFT算法存在明显的错误匹配。
5.2 精配准结果解析搜索的方法由于是逐点迭代运算、同时完成了副影像重采样,因此运算量十分巨大。在本试验中,相邻像元使用上一像元的偏移量结果作为初值进行迭代计算,同时利用盛金公式求解一元三次方程,有效减小运算量。正是由于是逐点计算,因此可以保证在整幅影像范围内配准精度比较均匀,不会受到内部局部变形的影响。
由于相关函数法和频谱极大值方法在本试验中配准精度未达到干涉要求,按照粗配准中拟合多项式系数无法生成干涉条纹图,因此在精配准过程中没有与本文方法作比较。
从精配准的结果看出,干涉条纹清晰,如图 5(a)所示;相干性较粗配准结果有了明显提高,如图 5(b)所示。解析搜索的方法很好地完成了影像的精配准。由于本试验中干涉影像对的基线较长,且飞行轨道存在一定夹角,多普勒值也不相同,导致方位向上出现比较密集的条纹。
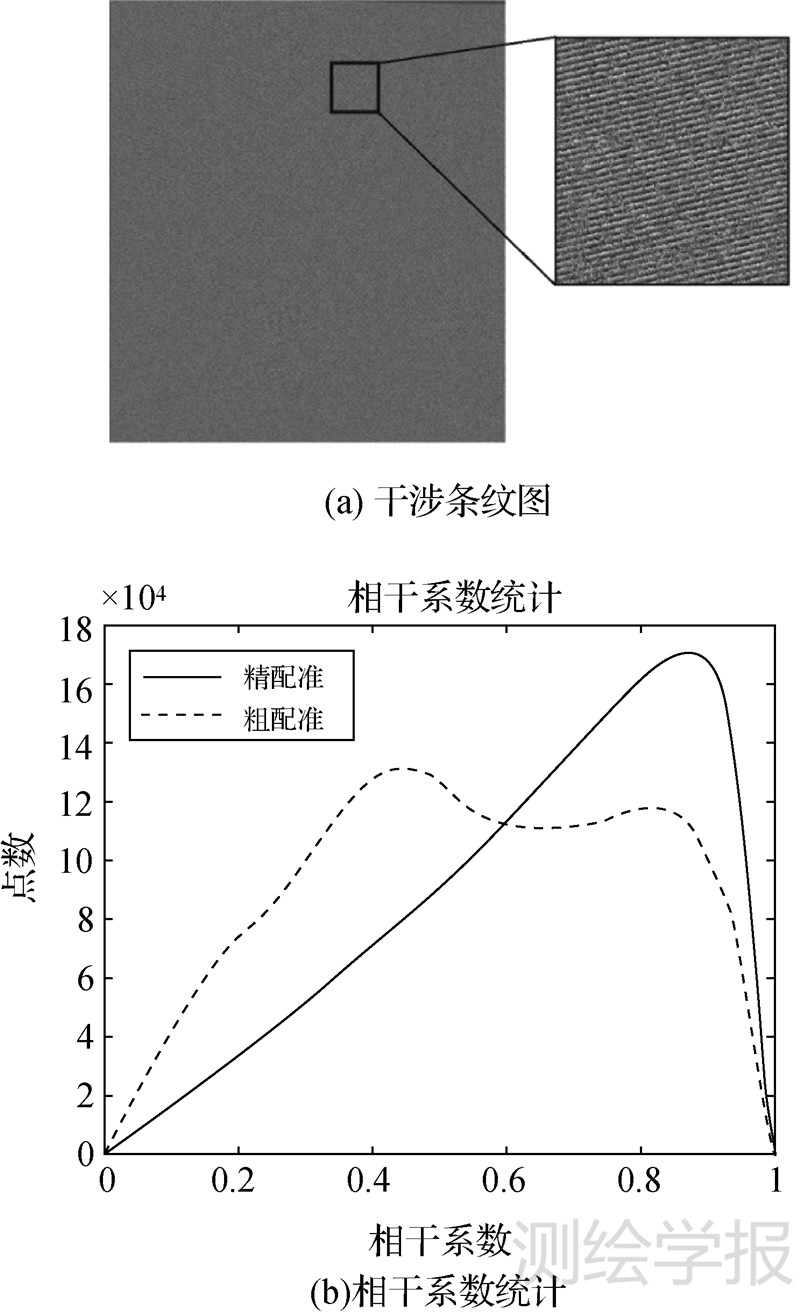
|
| 图 5 精配准后生成的干涉结果 Fig. 5 Interference results after the fine registration |
本文针对机载重复轨道干涉SAR数据相对变形较大,传统方法无法满足配准精度要求的问题,提出了一种基于改进的SIFT算法做粗配准、以解析搜索的方法为精配准的配准方法,提高了配准精度,解决了机载重轨干涉的配准问题。造成SIFT算法误匹配的一个重要原因是SIFT算法提取的特征向量并不完全适用于描述SAR影像的关键点,因此需要对SAR影像作进一步研究,改进SIFT算法对关键点的描述,使其能够更多地反映SAR影像的特性。由于试验区地形比较平坦,因此配准过程没有引入DEM,当遇到地形变化较大时可按照文献[15]的方法引入DEM辅助配准。
| [1] | LI F K, GOLDSTEIN R M. Studies of Multibaseline Space-borne Interferometric Synthetic Aperture Radars [J]. IEEE Transactions on Geoscience and Remote Sensing, 1990, 28(1): 88-97. |
| [2] | GABRIEL A K, GOLDSTEIN R M. Crossed Orbit Interferometry:Theory and Experiment Results from SIRB [J]. Remote Sensing, 1988, 9(5): 857-872. |
| [3] | LIN Q, VESECKY J F. New Approaches in Interferometric SAR Data Processing [J]. IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(3): 560-567. |
| [4] | ZHAO Zhiwei, YANG Ruliang, QI Haiming. An Improved Maximum Spectrum Peak Co-registration Algorithm for Space-borne InSAR Complex Data[J]. Acta Geodaetica et Cartographica Sinica, 2008,37(1):64-69.(赵志伟,杨汝良,祁海明. 一种改进的星载干涉SAR复图像最大频谱配准算法[J]. 测绘学报, 2008,37(1):64-69.) |
| [5] | TAO Qiuxiang, LIU Guolin. A New Method for Fine Registration of SAR Images in PS InSAR[J] . Acta Geodaetica et Cartographica Sinica, 2012,41(1):69-73.(陶秋香,刘国林. 永久散射体差分干涉测量技术中SAR影像精配准的一种新方法[J]. 测绘学报, 2012,41(1):69-73.) |
| [6] | WANG Qingsong, QU Jishuang, HUANG Haifeng, et al. A Method Based on Integrating Real and Complex Correlation Function for InSAR Image Coregistration[J]. Acta Geodaetica et Cartographica Sinica, 2012,41(4):563-569.(王青松,瞿继双,黄海风,等. 联合实、复相关函数的干涉SAR图像配准方法[J]. 测绘学报, 2012,41(4):563-569.) |
| [7] | ZHOU Zhiwei. High Resolution Space-borne Interferometric SAR Coregistration Methods Research[D]. Wuhan: Wuhan University, 2009.(周志伟. 高分辨率星载干涉SAR配准方法研究[D]. 武汉: 武汉大学, 2009.) |
| [8] | LOWE D G. Object Recognition from Local Scale-invariant Features [C]//Proceedings of International Conference on Computer Vision. Corfu: [s.n.], 1999:1150-1157. |
| [9] | LOWE D G. Local Feature View Clustering for 3D Object Recognition [C]//Proceedings of International Conference on Computer Vision and Pattern Recognition. Hawaii: [s.n.], 2001:682-688. |
| [10] | LOWE D G. Distinctive Image Features from Scale-invariant Keypoints [J]. International Journal of Computer Vision, 2004, 60(2):91-110. |
| [11] | WANG Daoyin. Research for Image Registration Based on Scale Invariant Feature Transform [D]. Hefei: University of Science and Technology of China, 2011. (汪道寅. 基于SIFT图像配准算法的研究[D]. 合肥: 中国科学技术大学, 2011.) |
| [12] | FENG Weiping. A Study on the Techniques of the Multifrequency and Multipolarization SAR Image Registration[D]. Hangzhou: Hangzhou Dianzi University, 2009. (冯卫平. 多波段多极化SAR图像配准技术研究[D]. 杭州:杭州电子科技大学, 2009.) |
| [13] | YUE Chunyu, JIANG Wanshou. An Automatic Registration Algorithm for SAR and Optical Images Based on Geometry Constraint and Improved SIFT[J]. Acta Geodaetica et Cartographica Sinica, 2012,41(4):570-576.(岳春宇,江万寿. 几何约束和改进SIFT的SAR影像和光学影像自动配准方法[J]. 测绘学报, 2012,41(4):570-576.) |
| [14] | CHUREESAMPANT K, SUSAKI J. Automatic Co-registration Performance of Fully Polarimetric SAR Images with Texture Relationship [C]//Proceedings of Geoscience and Remote Sensing Symposium. Vancouver: [s.n.], 2011:969-972. |
| [15] | NITTI D O, HANSSEN R F, REFICE A, et al. Impact of DEM-assisted Coregistration on High-resolution SAR Interferometry [J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(3):1127-1143. |
| [16] | LIU Baoquan, FENG Dazheng, WU Nan. Analytic Search Registration Approach for InSAR Image [J]. Journal of Data Acquisition & Processing, 2008, 23(6):646-651. (刘宝泉,冯大政,武楠. 干涉合成孔径雷达复图像配准解析搜索方法[J]. 数据采集与处理 2008, 23(6): 646-651.) |
| [17] | LIU Baoquan. Study on Key Techniques for Interferometric Synthetic Aperture Radar Measurement [D]. Xian: Xidian University, 2008. (刘宝泉. 干涉合成孔径雷达测量关键技术研究[D]. 西安: 西安电子科技大学, 2008.) |
| [18] | NATSUAKI R, HIROSE A. SPEC Method: A Fine Coregistration Method for SAR Interferometry [J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(1):28-37. |
| [19] | NATSUAKI R, HIROSE A. InSAR Local Co-registration Method Assisted by Shape-from-shading [J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013, 6(2):953-959. |
| [20] | DANUDIRDJO D, HIROSE A. Local Subpixel Coregistration of Interferometric Synthetic Aperture Radar Images Based on Fractal Models [J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(7):4292-4301. |
| [21] | LINDEBERG T. Scale-space Theory: A Basic Tool for Analysing Structures at Different Scales [J]. Journal of Applied Statistics, 1994, 21(2): 224-270. |
| [22] | SUN Jiachang. Spline Function and Computational Geometry [M]. Beijing: Science Press, 1982: 153-154. (孙家昶. 样条函数与计算几何[M]. 北京: 科学出版社, 1982: 153-154.) |
| [23] | FAN Shengjin. A New Extracting Formula and a New Distinguishing Means on the One Variable Cubic Equation [J]. Natural Science Journal of Hainan Teacheres College, 1989, 2(2): 91-98. (范盛金. 一元三次方程的新求根公式与新判别法[J]. 海南师范学院学报:自然科学版,1989, 2(2):91-98.) |