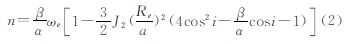2. 武汉大学 卫星导航定位技术研究中心,湖北 武汉 430079;
3. 武汉大学 测绘学院,湖北 武汉 430079
2. GNSS Research Center,Wuhan University,Wuhan 430079,China;
3. School of Geodesy and Geomatics,Wuhan University,Wuhan 430079,China
1 引 言
于2002年成功发射的GRACE卫星,在其运行的9年中,所提供的各种测量数据对于研究静态重力场和时变重力场影响重大,尤其是其提供的时变重力场模型,对于研究地球系统质量变化发挥了极大作用。但GRACE任务在取得巨大成功的同时,其中也包含很多不足之处,如数据本身的误差、时空混频误差等,都对重力场解算造成了极大的影响。经过数十年的研究,对于GRACE数据本身的误差已经考虑的越来越精细[1, 2, 3, 4, 5];混频误差也日益为人们所重视,目前已开展许多相关研究,并取得一系列有意义的成果[6, 7, 8, 9, 10]。
除了上述各种影响,由于轨道的衰减而导致星下点轨迹的变化也极大地影响了GRACE重力场反演的精度。在整个任务期内,由于推进器燃料的限制等,GRACE卫星并不能保持在同样的轨道高度不变。一致的星下点轨迹能够为重力场反演提供最好的条件,轨道的衰减使得卫星星下点轨迹时刻产生变化,并可能在某些轨道高度上出现星下点轨迹采样特别稀疏,密度变小的情况。这种变化对于长时间尺度的重力场解算来说影响并不大,如确定静态地球重力场,所使用的是连续数个月或数年的数据,一段时间内的稀疏数据并不会对解算精度产生较大影响,但是对于GRACE时变重力场的解算来说,这种影响不可忽略。因为这时所采用的是一个月或者更短时间间隔内的数据,不充足的数据采样会极大的影响重力场的解算精度[11 ,12]。文献[13]计算了CHAMP月重力场模型,结果表明误差过大以至于不能反映时变信号,而CHAMP卫星的短重复轨道周期是造成这种结果的一个重要原因。
在此背景下,笔者针对低轨道卫星的星下点轨迹特性进行了详细的分析研究,计算了各轨道参数对卫星重复周期的影响,并比较了不同轨道高度下由于重复周期不同所导致卫星月重力场解算结果的差异,提出长重复周期的卫星轨道特性能够为重力场解算提供较好的条件,在今后的重力卫星任务中,可以根据任务目标,设计较长重复周期的重复轨道,以提高重力场尤其是时变重力场解算的精度。
2 重复轨道及其计算方法 2.1 轨道重复周期对于互质的两个整数α和β,当卫星绕地球旋转β圈时,卫星的升交点绕地轴旋转α圈并且正好重复通过地球固定的同一个子午面,称卫星完成一个重复周期运动[14]。卫星轨道的重复周期与轨道高度关系密切,因为大气阻力等因素的影响其轨道高度会不断变化,如果没有推进器的作用,卫星不可能保持同一个重复轨道周期不变。并且根据Colombo-Nyquist规则,当卫星的重复轨道为β/α时,其能恢复重力场的最高阶为L=β/2,因此重复周期的大小对于重力场反演能力也有较大影响。要得到统一阶次的长时间尺度时变重力场模型,要么牺牲解算精度提供较高阶次的模型,要么牺牲完整的观测信息提供较低阶次的模型[15]。为我们所熟知的GOCE任务,就在其任务期内使卫星始终保持在重复轨道周期较长的轨道高度上,在很大程度上也是为了得到高精度的高阶静态重力场模型,尽量避免产生低密度和不规则的星下点轨迹,影响重力场解算精度[16, 17]。
因此在设计一个低轨卫星轨道时,必须使卫星的星下点轨迹尽量密集并且均匀分布,可以通过适当的轨道调整策略或者通过长的轨道重复周期设计以提高重力场解算的精度。
2.2 计算方法轨道重复周期与各轨道参数(轨道高度、轨道倾角和偏心率)相关。当卫星高度一定时,卫星的轨道周期(即卫星环绕地球一圈所需时间T)是确定的。本文只考虑J2项对卫星轨道的影响,并且J2=-C20(这里C20是正则化的),其所引起的轨道根数长期项变化仅在升交点赤经Ω、近地点角距ω和平近点角Μ项[18]。
共振角φβ/α[19]与恒星角S(相对一个固定的春分或者秋分点)的关系为
φβ/α=α(ω+M)+β(Ω-S)
令
M=nt+σ
则
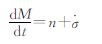
对上式求导可得
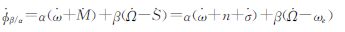
式中,n为轨道平均进动(轨道平均角速度),n= ;ωe为地球平均角速度。
;ωe为地球平均角速度。
当共振角 φβ/α为最小值,即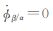 时,精确的轨道共振才发生。这时
时,精确的轨道共振才发生。这时
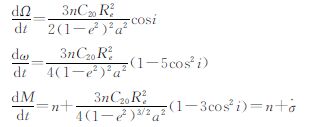
代入式(1),其中a=h+Re,h为卫星高度;i为卫星倾角;Re为地球半径。忽略e2项,可得
由于偏心率的存在,卫星轨道不可能保持精确的重复[20],但在本文的讨论中,考虑到小偏心率的情况(e=0.001),在上式中忽略e2项,得到重复轨道的近似计算公式。由式(2)可知,卫星高度h和卫星倾角i这两个参数,共同影响卫星重复周期β/α,改变其中任意一个参数,都可能引起卫星重复周期的巨大变化,尤其对于一个“自由下落”的卫星(如GRACE)来说,其轨道高度时刻在发生变化,理论上会遇到无限个数目的共振轨道,其星下点轨迹密度也在时刻发生变化,对于重力场反演,尤其是时变重力场的解算会有很大影响。
3 数值仿真目前在轨运行已近10年的GRACE卫星的轨道倾角为89°,这种倾角的卫星轨道能够更多地覆盖地球表面,得到全球分布的数据,适用于地球重力场的反演。本文针对类似GRACE卫星的倾角89°进行了数值仿真试验和分析,利用式(2)计算了在轨道倾角为89°时,轨道高度由250 km变化到500 km时卫星的重复轨道周期,结果如图 1所示,图中横坐标表示α,纵坐标为卫星高度h,红点上的数值表示β。

|
| 图 1 i=89°时卫星重复周期随高度变化图 Fig. 1 Variable repeat orbit when i=89° |
可以看出,当卫星倾角确定时,随着卫星高度的降低,轨道重复周期并不是线性变化的,在某些高度,会发生重复周期突然变短或者变长的现象。本文选取了其中几种轨道高度时,卫星重复周期的情况,具体参数见表 1。由表 1也可以看出,卫星的重复周期并不是与轨道高度的变化成一定的线性关系,而是没有固定的规律可循,并且重复周期越短的卫星任务,其星下点轨迹在赤道处的最大间隔也越大,会导致其星下点轨迹稀疏,空间分辨率降低。
| 轨道倾 角/(°) | 轨道高 度/km | α /d | β /圈 | 赤道上 间隔/(°) | 赤道上 间隔/km |
| 89 | 290 | 23 | 365 | 0.99 | 109.79 |
| 320 | 17 | 268 | 1.34 | 149.53 | |
| 350 | 44 | 689 | 0.52 | 58.16 | |
| 400 | 37 | 573 | 0.63 | 69.94 | |
| 407 | 2 | 31 | 11.61 | 1 292.74 | |
| 417 | 7 | 108 | 3.33 | 371.06 |
为了进一步研究重复周期对最终重力场解算的影响,基于上述各轨道高度,利用轨道积分仿真了星间距离为100 km的GRACE类型的一个月的卫星观测数据,包括轨道数据和星间距离变率数据,并利用这些数据基于动力学方法反演了月重力场。在计算中,轨道误差均给定为3 cm,星间距离变率误差给定为10-7 m/s,没有考虑非保守力的影响。轨道积分时真实重力场选为EIGEN-05C模型,反演时参考场选为EGM96模型,模型阶次均截断至60阶,整个计算过程除了轨道高度不同,其他各参数均选为相同。仿真结果如图 2和图 3所示。
|
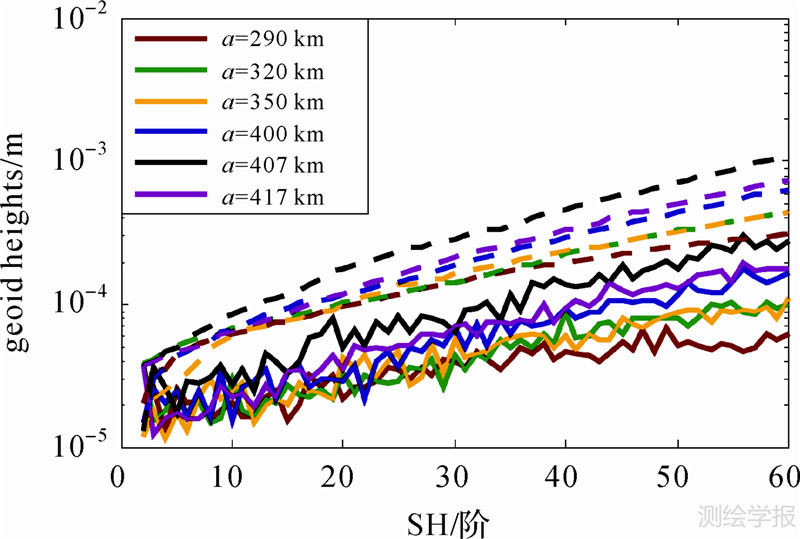
| 图 2 不同轨高时大地水准面的阶方差变化(实线为每阶的结果,虚线为累积结果) Fig. 2 Gravity field solutions for difference orbit altitude(solid lines represent difference degree variances of geoid heights between EIGEN-05C and the gravity solution and dashed ones represent the cumulative geoid errors) |
|
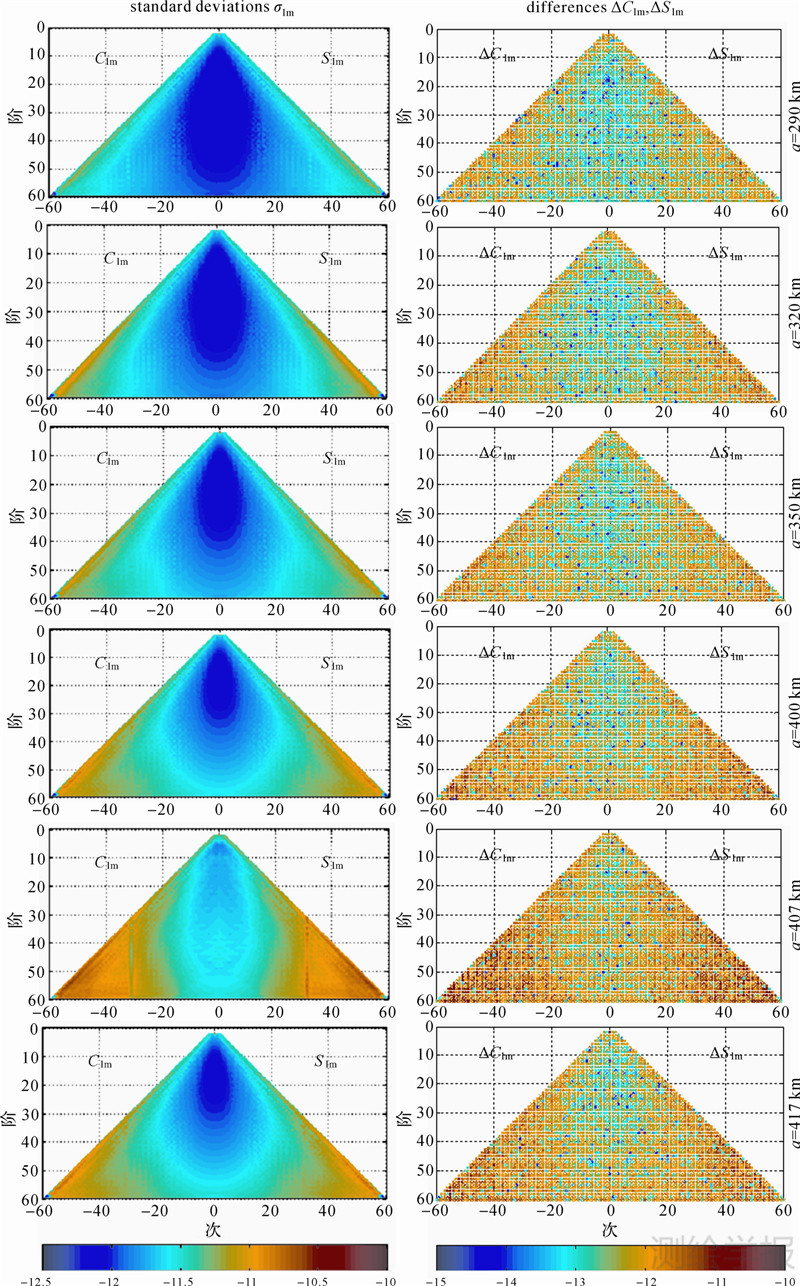
| 图 3 重力场球谐系数的误差图(左列:系数的方差分布;右列:与真实重力场系数差异的分布) Fig. 3 Spherical harmonic error spectra(left column: formal standard deviations; right column:actual EIGEN-05C and the gravity solution coefficient differences) |
本文的各个仿真试验仅在轨道高度不同的情况下做出,不同轨高的反向衰减因子(r/Re)2l+1作为球谐阶数l的函数,反映了由轨道高度变化导致的重力场误差的变化。由上式可知,轨道高度越高(即r越大),反演的重力场的精度越低,对于反演高分辨率的重力场来说,较低的卫星轨道高度比相对较高的轨道高度要好。从图 2也可以看出仿真结果基本满足这一规律,随着轨道高度的降低,大地水准面的阶方差呈减小的趋势,重力场反演精度在升高。但同时发现,当轨高为407 km时,重力场精度较417 km轨道高度的情况还要低,虽然轨高为417 km时卫星的轨道重复周期也不长,会对其重力场解算造成影响,但从图中明显看出,其在各阶的精度基本都高于轨高为407 km时的情况。本文的仿真过程已经排除了有其他误差的影响因素,因此这一结果用轨道的短重复周期来解释最为合适,轨高为407 km时,卫星的重复周期只有2天,星下点轨迹在赤道处的间隔宽达1 292.74 km,空间分辨率极小,极大地影响了重力场解算的精度。同时也可以注意到,轨道高度为320 km和350 km的重力场精度在同一量级上,图中可以看出,其累积的大地水准面阶方差曲线极为相近,尤其是40~60阶上几乎重合。这是由于轨高为320 km时的重力场高阶部分精度应比轨高为350 km时的高,但同时,350 km时轨道的重复周期长,星下点轨迹密集,使重力场解算的精度得到提高,因此,这2个轨道高度最终重力场解算精度趋于一致。图 3给出了不同轨道高度时解算的重力场系数的误差分布,从图中也可以看出,当a=407 km时,所得重力场系数的方差精度最低,而a=320 km和a=350 km时的误差谱图几乎一致。
4 结 论目前由于短重复轨道周期所导致的月重力场精度降低的问题,国际上有不同的观点。一种观点认为,需要使用轨道调整策略使得卫星轨道跳过这样一个低次共振的阶段并远离它;另一种观点则认为这种低次共振轨道相对于卫星任务的寿命来说只是一个相对较短的现象,不需要特别调整,可以让轨道以一种“自然下落”的状态发展[8]。
从本文的仿真结果来看,短重复周期的轨道对于重力场的解算精度,尤其是短时间的时变重力场会造成较大影响,因此应该尽量避免卫星运行在这种轨道上。并且,在地球观测任务中,重复星下点轨迹结构尤其有用,它使得卫星在一段时间间隔后重复飞过地球表面的同一区域,周期性的星下点轨迹能够校准和复查在特殊观测区域的观测量,比如气候的变化和地质现象。基于以上原因,在将来的重力卫星任务中,应该考虑将卫星设计为重复周期轨道,通过推动器等装置使卫星一直保持在一个给定高度上,保持一个较长周期的重复轨道。另一种考虑是,可以使用卫星编队的方式来避免短重复周期。这样的卫星参数该如何选择,还需要在将来的工作中作进一步深入的研究讨论。
| [1] | WAHR J, SWENSON S, VELICOGNA I, et al. Accuracy of GRACE Mass Estimates[J]. Geophysical Research Letters, 2006, 33( L06401): 1-5. |
| [2] | FROMMKNECHT B. Integrated Sensor Analysis of the GRACE Mission[M]. München:Sudwestdeutscher Verlag fur Hochschulschriften, 2009. |
| [3] | FLURY J, BETTADPUR S, TAPLEY B, et al. Precise Accelerometry Onboard the GRACE Gravity Field Satellite Mission[J]. Advances in Space Research, 2008, 42(8): 1414-1423. |
| [4] | HORWATH M, LEMOINE J M, BIANCALE R, et al. Improved GRACE Science Results after Adjustment of Geometrix Biases in the Level-1B K-band Ranging Data[J]. Journal of Geodesy, 2011, 85(1): 23-38. |
| [5] | ZHAN Jingang, WANG Yong, HAO Xiaoguang. Improved Method for Removal of Correlated Errors in GRACE Data[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 442-446. (詹金刚,王勇,郝晓光. GRACE时变重力场位系数误差的改进去相关算法[J]. 测绘学报, 2011, 40(4): 442-446.) |
| [6] | RAY R D, LUTHCKE S B. Tide Model Errors and GRACE Gravimetry: Towards a More Realistic Assessment[J]. Geophysical Journal International, 2006,167(3): 1055-1059. |
| [7] | SEO K W, WILSON C R, HAN S C, et al. Gravity Recovery and Climate Experiment(GRACE) Alias Error from Ocean Tides[J]. Journal of Geophysical Research, 2008,113(B12): 3405-3414. |
| [8] | SEO K W, WILSON C R, CHEN J, et al. GRACE’s Spatial Aliasing Error[J]. Geophysical Journal International, 2008, 172(1): 41-48. |
| [9] | HAN S C, JEKELI C, SHUM C K. Time-variable Aliasing Effects of Ocean Tides, Atmosphere, and Continental Water Mass on Monthly Mean GRACE Gravity Field[J]. Journal of Geophysical Research, 2004, 109(B4): 4403-4412. |
| [10] | ZHAO Qian, JIANG Weiping, XU Xinyu, et al. Influence Analysis of Aliasing Effects on GRACE Gravity Solution[J]. Journal of Geodesy and Geodynamics, 2011, 31(4): 123-126. (赵倩,姜卫平,徐新禹,等. GRACE卫星重力场解算中混频误差影响的探讨[J]. 大地测量与地球动力学, 2011, 31(4): 123-126.) |
| [11] | KLOKOCNIK J, KOSTELECKY J, GOODING R H. On Fine Orbit Selection for Particular Geodetic and Oceanographic Missions Involving Passage through Resonances[J]. Journal of Geodesy, 2003, 77(1/2): 30-40. |
| [12] | YAMAMOTO K, OTSUBO T, KUBOOKA T, et al. A Simulation Study of Effects of GRACE Orbit Decay on the Gravity Field Recovery[J]. Earth Planets Space, 2005, 57: 291-295. |
| [13] | SNEEUW N, GERLACH C, FOLDVARY L, et al. One Year of Time-variable CHAMP-only Gravity Field Models Using Kinematic Orbits[C]//A Window on the Future of Geodesy: 128[M]. Berlin: Springer, 2005: 288-293. |
| [14] | GOODING R H, WAGNER C A, KLOKOCˇNIK J, et al. CHAMP and GRACE Resonances and the Gravity Field of the Earth[J]. Advances in Space Research. 2007, 39(10): 1604-1611. |
| [15] | WAGNER C, MCADOO D, KLOKOCˇNK J, et al. Degradation of Geopotential Recovery from Short Repeat-cycle Orbits: Application to GRACE Monthly Fields[J]. Journal of Geodesy, 2006, 80(2): 94-103. |
| [16] | BEZDEK A, KLOKOCNIK J, KOSTELECKY J, et al. Simulation of Free Fall and Resonances in the Forthcoming GOCE Mission[C]//Proceedings of EGU General Assembly 2009. Vienna: EGU, 2009: 2980-2986. |
| [17] | KLOKOCNIK J, WAGNER C A, KOSTELECKY J, et al. Variations in the Accuracy of Gravity Recovery due to Ground Track Variability: GRACE, CHAMP, and GOCE[J]. Journal of Geodesy, 82(12): 917-927. |
| [18] | KAULA W M. Theory of Satellite Geodesy[M]. Mineola: Dover Publications Inc, 1996. |
| [19] | GOODING R H, KING-HELE D G. Explicit forms of Some Functions Arising in the Analysis of Resonant Satellite Orbits[J]. Proceedings of the Royal Society of London: Mathematical and Physical Sciences, 422(1863): 241-259. |
| [20] | COLOMBO O L. Altimetry, Orbits and Tides[R]. Washington D C: National Aeronautics and Space Administration, 1985. |