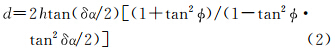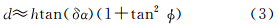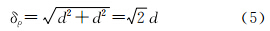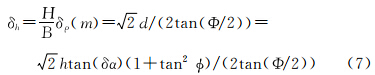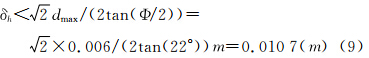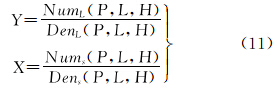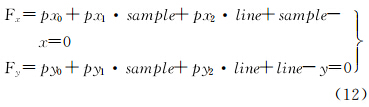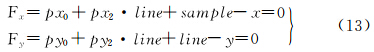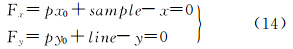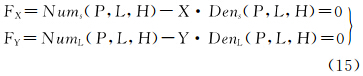2. 武汉大学 测绘遥感信息工程国家重点实验室,湖北 武汉 430079
2. State Key Laboratory of Information Engineering in Surveying, mapping and Remote Sensing, Wuhan University, Wuhan 430079,China
1 引 言
资源三号测绘卫星是中国首颗民用高分辨率光学传输型立体测图卫星,主要搭载有一台地面分辨率2.1m的高分辨率正视全色延时积分成像(TDI CCD)相机、两台地面分辨率优于3.6m的前视、后视全色TDI CCD相机和一台地面分辨率优于6.0m的正视多光谱相机。资源三号测绘卫星集测绘和资源调查功能于一体,用于长期、连续、稳定、快速地获取覆盖全国的高分辨率立体影像和多光谱影像以及辅助数据,生产全国基础地理信息1∶5万测绘产品,开展1∶2.5万以及更大比例尺地图的修测和更新,开展国土资源调查和监测(参见http://www.sasmac.cn/portal_space)。因此与采用国外商业卫星遥感影像进行测图相比,建立中国自主的测绘卫星的成像几何模型,进而生产影像产品和测绘产品,是卫星测绘应用的核心技术问题。
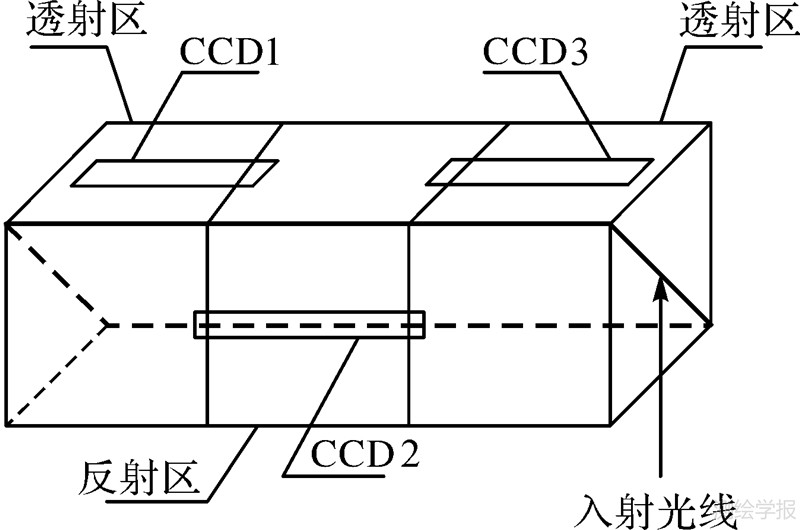
资源三号测绘卫星是线阵推扫式光学卫星,3台全色相机采用的透射式测绘相机,幅宽均大于50km。相机的CCD采用了线阵拼接的方案。其中,前后视相机是4片TDI CCD拼接,正视相机是3片TDI CCD拼接,如图 1所示。正视相机是将3片CCD在焦面上交错安装在透射区和反射区上,形成近似直线的一条连续CCD阵列。
|
| 图 1 资源三号测绘卫星正视相机CCD拼接示意图 Fig. 1 ZY-3 surveying satellite nadir camera’s CCD splicing |
由于多个CCD线阵的安装精度以及TDI CCD沿轨方向宽度等因素的限制,多CCD在焦平面不可能形成一条严格意义上的CCD线阵。在实际的摄影测量数据生产中,一般使用卫星影像供应商提供的按照成像几何特性和辐射特性拼接后的影像,如IKONOS[1]和WorldView-2[2, 3]等进行摄影测量处理。影像的拼接精度会直接影响后续摄影测量生产的精度,如在利用IKONOS-2立体像对匹配生产数字高程模型(DEM)时,拼接精度不高会导致DEM精度的损失[4]。因此利用拼接后的影像建立成像模型是实现卫星高精度立体测图的关键问题[5]。法国、美国等国家由于有各自本国的卫星,对这一问题研究较为深入,如何对中国自主的首颗测绘卫星进行拼接,进而构建中国民用测绘卫星的成像几何模型是实现国产民用测图卫星高精度测图的关键。
针对上述问题,本文利用基于虚拟CCD 线阵成像技术的视场拼接方案,在焦平面上构造出无畸变的CCD阵列,对原始多个CCD的影像按照理想的线中心投影成像方式进行重新排列,实现了多个CCD影像的几何和辐射无缝拼接。在此基础上,建立拼接后影像的严密成像几何模型和有理函数模型(RFM),利用资源三号测绘卫星传感器校正产品进行不同控制点情况下的区域网平差试验,生产DSM和DOM,验证了资源三号测绘卫星传感器校正产品的几何精度。
2 资源三号测绘卫星三线阵成像几何模型的构建 2.1 基于虚拟CCD阵列的传感器校正产品要求为满足国产民用卫星立体测图的需求,需要对卫星的原始数据进行辐射和几何处理,形成不同级别的影像产品。资源三号测绘卫星的传感器校正产品是对0级产品经辐射校正和传感器校正处理后形成的影像产品,产品带有严密成像几何模型和RFM模型,但未作系统几何纠正,是进行实际测图的标准影像(该产品和Worldview-2的basic产品[3]以及Pleiades 的level1类似[5])。
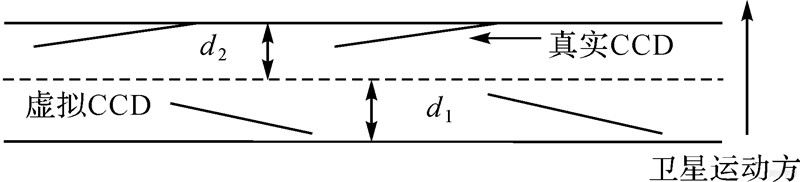
资源三号测绘卫星相机采用多片CCD拼接而成,为了形成“整景”和“整条带”的影像,采用虚拟CCD的方法,即以多个CCD沿轨道方向安装的位置为基准,将虚拟CCD“安装”在多个CCD沿轨道方向的中心线上。如图 2所示,其中实线表示实际的多个CCD线阵,虚线表示虚拟的CCD,d1、d2分别表示虚拟CCD与真实CCD沿着轨道方向的最大距离。
|
| 图 2 虚拟CCD和实际CCD在焦面位置相对关系示意图 Fig. 2 Relative position for virtual CCD and practical CCD in the focal plane |
虚拟CCD影像需达到如下要求: ① 垂直轨道方向的影像为理想的无畸变的线中心投影;② 沿轨道方向的虚拟线阵的积分时间一致,无积分时间跳变。
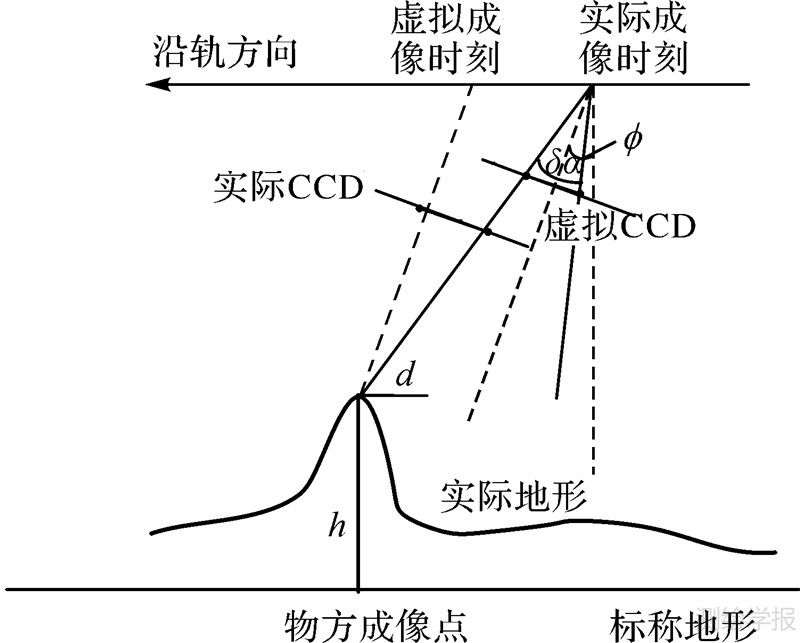
2.2 虚拟CCD和实际CCD沿轨方向像差分析虚拟CCD的“安装”位置和真实CCD的安装位置在沿轨方向上存在偏差,该偏差将导致同轨立体或二/三线阵同轨立体成像处理高程精度的损失。图 3为推扫式成像过程中垂直于CCD线阵的截面图。图中虚拟CCD、实际CCD与截面的交点(图中黑点所示)成像光线指向存在δα的角度差,φ为δα的角平分线与垂线的交角。
|
| 图 3 CCD影像拼接误差影响因素图 Fig. 3 Factors for the CCD image splicing error |
当虚拟CCD探元光线的物方投影点的高程(图中为标称地形高程)与该点真实高程的差值为h时(如图 3所示),该地形起伏产生的像差d(为物方距离)为
根据三角函数性质,将公式(1)展开得到公式(2)
由于虚拟CCD和实际CCD安装相对于投影中心的角度δα≈0,因此tan(δα/2)≈tan(δα)/2。在实际形成同轨立体中,φ<45°(资源三号测绘卫星为22°),因此tanδα≈0,tanφ<1,则有1-tan2φ·tan2δα/2≈1。公式(2)可以近似为
在摄影测量中,有
式中,H为航高;B为基线;δρ为视差的标准差;δh为高程误差。根据误差传播定律,视差的标准差δρ可以表示为
在航天摄影测量中,高基比H/B可以由立体像对的交会角求得
式中,Φ为立体像对的交会角,在资源三号测绘卫星前、后视形成的立体像对中,根据卫星的设计参数可知,交会角为22°+ 22°(前视、后视的测摆角度相加)。
将式(5)、(6)代入式(4)中有
由式(3)可知,虚拟成像过程中,当δα趋近0时,即虚拟CCD安装位置与真实CCD位置偏差很小时,因采用平均高程面引起的像差D也趋近为0,由此引起的高程误差δh可以忽略。在该情况下,可采用该成像区域平均高程,而不需要精确的DEM。
当δα取值不能被忽略,即虚拟CCD安装位置与真实CCD安装位置偏差较大时,需要根据δα和对高程精度δh的要求,来选取合适精度的DEM用于拼接;此时,h便体现为DEM的精度,根据式(3),当DEM精度足够高时,h足够小,d的取值也趋近为0。以资源三号测绘卫星前视相机为研究对象,分析重成像过程引起的像差,进而分析该像差对高程精度的影响。根据实验室的前视相机的多片CCD沿着轨道向的安装范围测量值,虚拟CCD与原始各CCD沿轨道向的指向角δα<0.00075°,前视φ=±22°。根据式(3),对于本文试验区——大连地区,地形起伏所引起的像差为
根据公式(7),把像差换算为高程精度,则对于大连地区有
考虑到摄影测量过程中的选点误差,该高程精度损失相对较小。因此,在实际算法应用中使用平均高程带来的高程精度损失可以忽略不计。
2.3 基于虚拟CCD重成像算法各片CCD中的每个CCD探元在相机坐标系下的指向角为(ψX,ψY),表示每个探元摄影光束在相机坐标系下的几何关系[5, 6]。同样,根据虚拟CCD的“安装”位置,按照理想线中心投影成像原理,计算虚拟CCD每个探元在相机坐标系的指向角。在此基础上,按照如下步骤进行基于虚拟CCD的影像拼接:
(1) 将虚拟CCD影像上任意一个像点,利用像点所对应探元的指向角、实际轨道参数和姿态参数,建立虚拟CCD影像严密成像几何模型[7] ,利用该模型将像点投影到SRTM-DEM或该成像区域平均高程面上,得到该点对应的大地坐标;
(2) 根据实际CCD影像的严密成像几何模型,将第1步中求得的大地坐标投影到实际CCD影像上;
(3) 对实际CCD成像影像灰度进行重采样,赋予虚拟探元重成像对应的像素;
(4) 重复以上步骤获取整个成像范围的重成像影像。
2.4 传感器校正产品的成像几何模型传感器校正产品的几何模型指的是地物点的影像坐标(x,y)和地面坐标(X,Y,Z)之间的数学关系[7, 8],包含2类,第1类是严密成像几何模型,第2类是通用成像几何模型。
基于线阵CCD成像瞬间各CCD探元扫描地面的视线方向矢量构建资源三号测绘卫星传感器校正产品的严密成像几何模型,通过解求成像瞬间各CCD探元的视线方向与地球椭球模型的交点,建立像点与地面点之间一一对应的关系[6, 7, 8]。
针对资源三号测绘卫星下传数据,GPS测定的是GPS相位中心的位置,姿态敏感器测定的是星敏到J2000坐标系下的指向。为了得到相机主光轴的位置和姿态,需要将GPS和星敏测定的数据转为相机的位置和指向。因此需通过地面测定GPS相位中心在卫星本体坐标系中3个偏[Dx Dy Dz]T以及星敏感器本体系和卫星本体系之间的坐标旋转关系Rstarbody、相机在卫星平台上安装矩阵Rcamerabody和[dx dy dz]T以及虚拟CCD线阵上每个像素在相机坐标系的指向角(ψX,ψY)等。据此在不考虑大气折射影响的条件下,构建资源三号测绘卫星传感器校正产品的严密成像几何模型,即
式中,[X Y Z]WGS-84T表示地面一点P在WGS-84下的三维笛卡儿坐标;m为比例系数;f为相机主距。
为了方便资源三号测绘卫星的数据处理,本文在构建传感器校正产品严密几何模型的基础上,同样构建资源三号测绘卫星的RFM模型。
RFM模型将地面点大地坐标与其对应的像点坐标用比值多项式关联起来。为了增强参数求解的稳定性,将地面坐标和影像坐标正则化到-1和1之间。对于一个影像,定义如下比值多项式[7, 9]
根据文献[7,9—10],求解RFM模型参数:根据影像覆盖范围,利用美国地质调查局提供的全球1 km分辨率DEM,根据公式(11)计算该传感器校正产品覆盖区域的最大最小椭球高。然后,在高程上以一定间隔分层,在平面上,以一定的格网大小建立地面规则格网,生成控制点地面坐标,最后利用传感器校正产品的严密几何模型的反变换模型(公式(12)),计算控制点的影像坐标。通过加密控制格网和层,建立独立检查点。利用控制点坐标用计算传感器校正产品坐标和地面坐标的归一化参数,将控制点和检查点坐标归一化。采用最小二乘平差原理解求RFM模型参数[7],从而获得资源三号测绘卫星卫传感器校正产品的RFM模型参数,并用检查点进行精度检查。
3 资源三号测绘卫星摄影测量处理 3.1 资源三号测绘卫星传感器校正产品区域网平差模型资源三号测绘卫星影像的RFM模型采用与地面无关的模式,采用传感器校正产品的严密几何成像模型,存在一定的系统性误差[7, 10]。因此可以通过影像自身之间的约束关系和一定数量的控制点补偿有理函数模型的系统误差来提高定位精度,这就是基于有理函数模型的区域网平差。
分析卫星系统参数对影像几何精度的影响,需要改正两类误差,一类参数纠正行方向的误差,一类参数纠正列方向的误差。其中行参数吸收轨道、姿态在行方向上的影响,列参数吸收轨道、姿态在列方向上的影响[11, 12, 13, 14, 15],因此可以采用定义在影像面的仿射变换、平移变换、比例变换等来校正此类误差。可以在影像上定义变换
式中,(x,y)是控制点在传感器校正产品影像上的量测坐标;(sample,line)为地面控制点利用RFM模型参数投影到影像面的投影值,该变换参数和RFM模型参数一起等同传感器校正产品的严密几何模型的卫星系统参数,本文采用直接列改化法方程的策略,消除一类连接点地面坐标未知数,仅仅保留像面的变换系数,然后采用和经典光束法平差一样的模式进行平差[7]。
3.2 资源三号测绘卫星传感器校正产品立体定向模型本文通过基于RFM模型的空间前方交会进行立体定向。根据RFM模型公式(11)进行公式变形可得
分别对经纬度以及高程求导线性化,所得误差方程为
式中, ;x=[lat lon hei]T;W为权矩阵。
;x=[lat lon hei]T;W为权矩阵。
由于公式(16)是公式(15)线性化得近似公式,所以在求解的过程中需要初值进行迭代计算。经纬度的初值可由平均高程和像点坐标利用RFM模型正算获得[7]。
4 试验验证和分析 4.1 试验数据本文试验数据采用2012年1月11日获取的大连地区的资源三号测绘卫星三线阵影像,影像大小为50km×50km,为平原和丘陵地形,为了验证资源三号测绘卫星的几何精度,利用CORS,在地面量测了18个GPS点,其中2个点位附近为双点,精度优于0.1m,像点量测精度为0.5像素。
4.2 RFM模型传感器校正产品精度利用2.4节的处理技术,对大连地区资源三号测绘卫星的三线阵数据进行RFM模型替代严密几何模型的精度试验,采用400像素×400像素的像面格网,采用高程分层为15,求解分母不相等的三阶RFM模型参数[7],精度如表 1所示。资源三号测绘卫星正视的RFM模型替代严密几何模型的精度0.04%像素,前视和后视均为0.1%像素,因此资源三号测绘卫星前正后视传感器校正产品的RFM模型替代严密几何模型的精度均优于5%像素,满足摄影测量生产的需求[7]。
| 像素 | |||||||
| X | Y | 平面 | |||||
| 最大 | 中误差 | 最大 | 中误差 | 最大 | 中误差 | ||
| 正视 | 检查点 | 1.50E-03 | 3.47E-04 | -1.26E-03 | 3.19E-04 | 1.72E-03 | 4.72E-04 |
| 控制点 | -1.52E-03 | 3.46E-04 | -8.01E-04 | 2.86E-04 | 1.59E-03 | 4.48E-04 | |
| 前视 | 检查点 | -4.14E-03 | 1.16E-03 | -2.83E-03 | 6.33E-04 | 4.90E-03 | 1.32E-03 |
| 控制点 | -4.20E-03 | 1.16E-03 | -1.84E-03 | 5.46E-04 | 4.25E-03 | 1.28E-03 | |
| 后视 | 检查点 | 3.21E-03 | 1.04E-03 | -2.54E-03 | 6.51E-04 | 3.77E-03 | 1.23E-03 |
| 控制点 | -4.22E-03 | 1.08E-03 | -1.63E-03 | 5.78E-04 | 4.32E-03 | 1.23E-03 | |
为了验证哪种RFM参数精化模型适合于资源三号测绘卫星的传感器校正产品,特进行分组试验,具体试验方案见表 2,并进行了前正后三视和前后两视试验,验证正视影像加入平差,对提高平面精度或者高程的作用。表 3为三视影像平差结果,表 4为两视影像平差结果。对比表 3和表 4,三视和两视影像的平差结果,高程精度基本一致,平面精度略有提升,符合资源三号测绘卫星设计思路,高程精度决定于前后视的交会角,增加一个正视的影像,增加了观测值,提高了平面定位精度。
| 类别序号 | 描述 |
| 1 | 所有点利用RFM模型参数进行直接空间前方交会 |
| 2 | 1个控制点采用公式(14)作为RFM模型参数精化模型进行区域网平差,其余点当做检查点 |
| 3 | 2个控制点采用公式(13)作为RFM模型参数精化模型进行区域网平差,其余点当做检查点 |
| 4 | 3个控制点采用公式(12)作为RFM模型参数精化模型进行区域网平差,其余点当做检查点 |
| 5 | 4个控制点采用公式(12)作为RFM模型参数精化模型进行区域网平差,其余点当做检查点 |
| 6 | 所有的点控制点采用公式(12)作为RFM模型参数精化模型进行区域网平差,无检查点 |
| m | ||||||||
| 控制点 | 检查点 | |||||||
| X | Y | 平面 | 高程 | X | Y | 平面 | 高程 | |
| 1 | 4.292 | 6.119 | 7.475 | 36.580 | ||||
| 2 | 0.000 | 0.000 | 0.000 | 0.001 | 4.008 | 5.549 | 6.845 | 37.443 |
| 3 | 0.000 | 0.000 | 0.000 | 0.000 | 2.260 | 3.484 | 4.153 | 16.031 |
| 4 | 0.000 | 0.000 | 0.000 | 0.000 | 2.341 | 2.154 | 3.181 | 1.768 |
| 5 | 2.151 | 1.113 | 2.422 | 0.570 | 2.037 | 2.169 | 2.975 | 1.787 |
| 6 | 2.011 | 1.944 | 2.797 | 1.299 | ||||
| m | ||||||||
| 控制点(RMS) | 检查点(RMS) | |||||||
| X | Y | 平面 | 高程 | X | Y | 平面 | 高程 | |
| 1 | 4.188 | 9.676 | 10.543 | 37.000 | ||||
| 2 | 0.000 | 0.000 | 0.000 | 0.000 | 4.183 | 8.920 | 9.852 | 38.185 |
| 3 | 0.000 | 0.000 | 0.000 | 0.000 | 3.470 | 6.229 | 7.130 | 16.394 |
| 4 | 0.000 | 0.000 | 0.000 | 0.000 | 2.412 | 2.203 | 3.266 | 1.801 |
| 5 | 1.893 | 1.379 | 2.342 | 0.570 | 2.193 | 2.185 | 3.095 | 1.816 |
| 6 | 1.920 | 1.926 | 2.720 | 1.303 | ||||
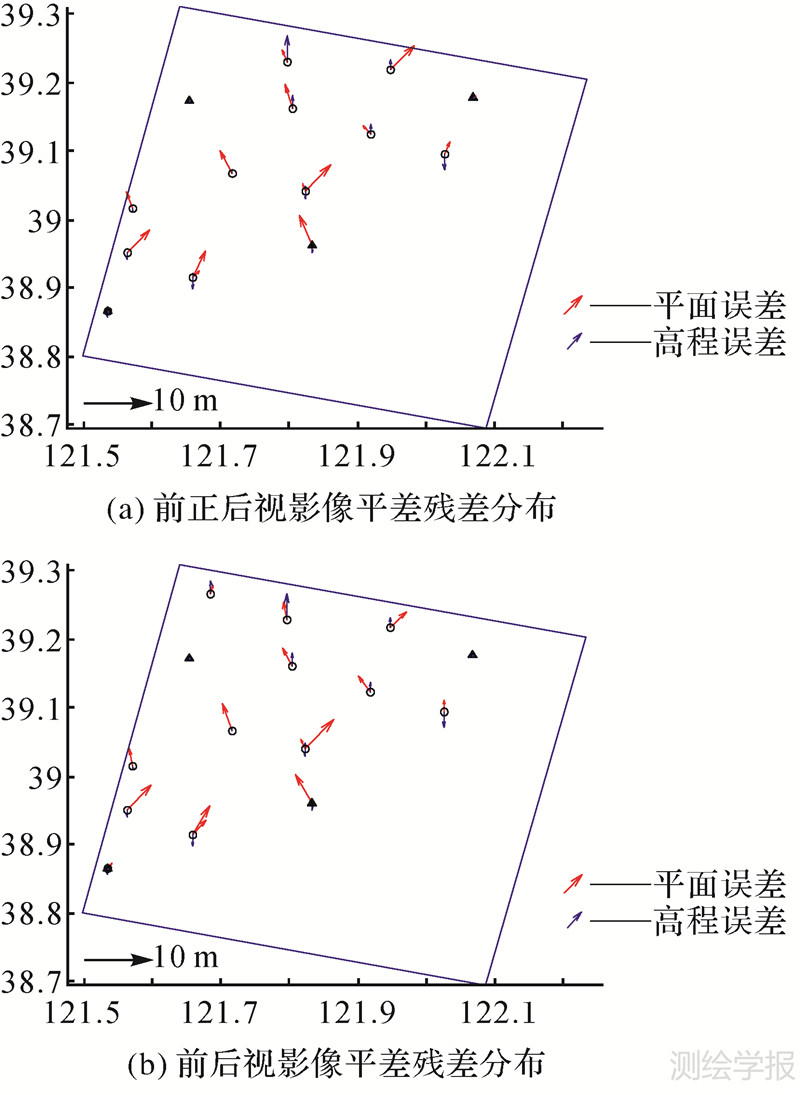
根据文献[16],在采用仿射变换的RFM模型参数精化模型时,四角布控方案可以获得最高的平差精度,三视和两视情况的区域网平差中的平面和高程残差如图 4(a)和(b)所示,无论哪种情况基本符合控制点控制区域重心位置的高程残差小,越靠近边缘,高程的残差大的规律,因此控制点布设应尽可能靠近立体重叠影像边缘,充分控制感兴趣区域。
|
| 图 4 四角点布设控制点位残差分布图 Fig. 4 Ground control points residual plots in four corners |
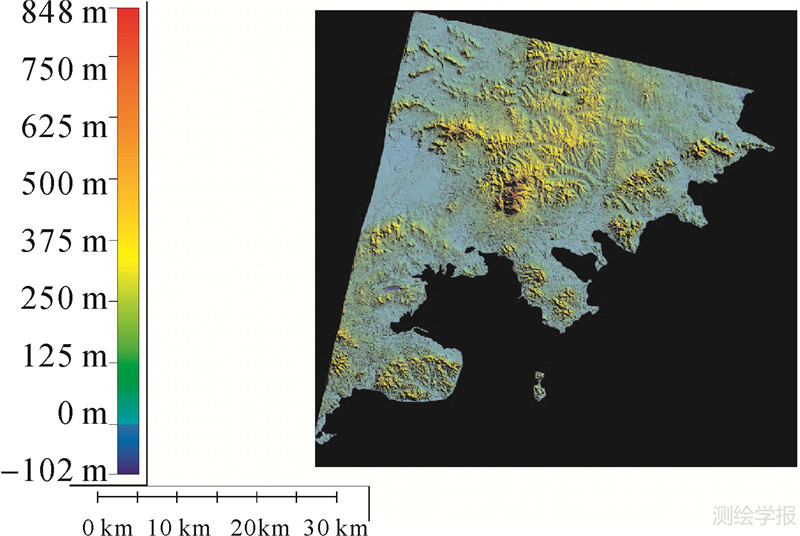
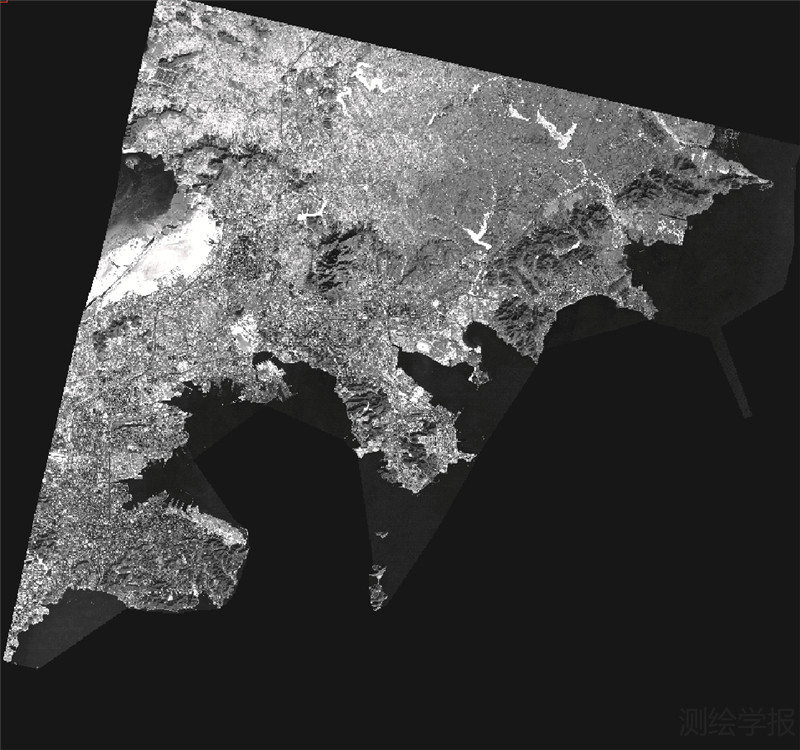
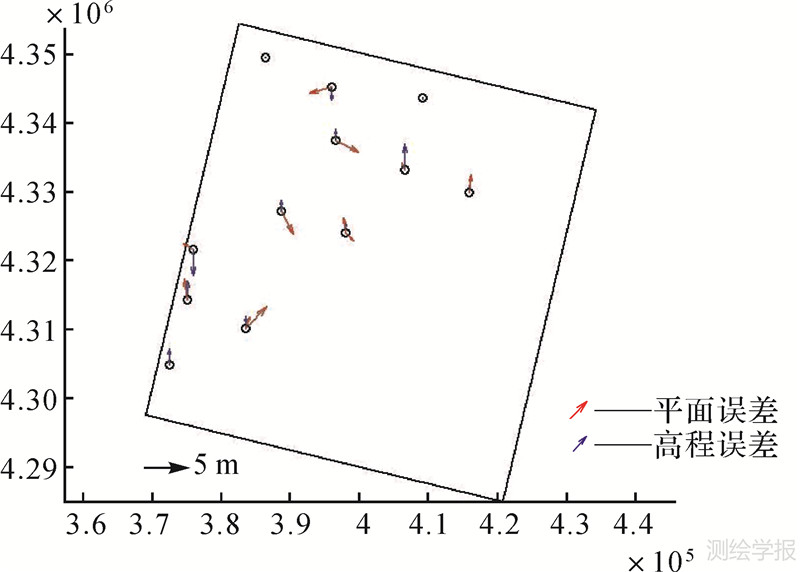
将前正后视影像利用4个控制点平差后,采用密集匹配技术[17, 18, 19]生产该区域的DSM(如图 5所示),在此基础上生产正射影像[7](如图 6所示),利用其余14个GPS点作检查点,检查结果如图 7所示,其中DSM的高程中误差为2.07m,最大误差为3.767m,正射影像的平面中误差为2.93m,最大误差为4.38m。
|
| 图 5 前后视影像自动匹配生成的DSM示意图 Fig. 5 DSM generated from forward and backward image matching |
|
| 图 6 利用正视影像和自动匹配生成的DSM生产的DOM示意图 Fig. 6 DOM generated from forward and backward image matching’s DSM |
|
| 图 7 DSM和DOM独立检查点残差图 Fig. 7 DSM and DOM check points residual plots |
试验结果分析如下:
从表 2~4可以看出,资源三号测绘卫星三线阵传感器校正产品RFM模型替代严密几何模型的精度均优于0.1%,满足摄影测量对几何模型的要求。
从表 6、7可以看出,无控制点条件下的直接空间前方交会获得的地面点坐标的精度比较差,前正后三线阵影像平面中误差为7.475m,高程中误差为36.580m,前后视两线阵影像平面中误差为10.543m,高程中误差为37.000m;四角点布设控制点条件下的前方交会获得的地面点坐标的精度大幅度提高,前正后三线阵影像平面中误差为2.975m,高程中误差为1.787m,前后视两线阵影像平面中误差为2.266m,高程中误差为1.816m;在有少量控制点后平面高程精度大幅度提高说明三线阵影像有明显的系统偏差。
从表 6、7第5组、第6组试验可以看出,采用4个点和所有点都当做控制点时高程精度没有很明显的提高,说明4个控制点建立的像面仿射变换精化RFM模型参数能完全消除资源三号测绘卫星的误差。
5 结论及建议根据资源三号测绘卫星第一景影像的处理结果,虚拟CCD拼接重成像引起的高程损失为0.0107m,相对于资源三号测绘卫星前后视沿着轨道方向的分辨率3.6m而言,损失为0.003像素,基本无损。该方法可以用于资源三号测绘卫星应用系统建设。RFM模型替代前正后视影像的严密几何模型的及高度均优于0.1%像素,也可用于资源三号测绘卫星严密几何模型的替代,精度无损。
本文采用的像面仿射变换模型加RFM模型在四角点布控方案可以获得较高的平差精度,平面为3.2m,高程为1.8m;在此基础上进行DSM产生和DOM生产,DSM精度为2.07m,DOM精度为2.92m,可以满足1∶5万地形测图规范要求可为后续资源三号测绘卫星的4D产品生产提供指导作用。
本文主要针对第一颗民用测绘卫星的第一轨影像进行快速处理得到的初步成果。由于卫星的轨道还没有完全稳定,相机还要进行一系列调整,姿态数据还没有全部下传,因此后续还需要进行大量的轨道、姿态后处理、几何检校、以及开展不同地形、不同轨道等区域的大量在轨测试工作。
资源三号测绘卫星三线阵影像从平差结果和生产的DSM/DOM检查精度来看,已经达到了国外成熟商业卫星同等分辨率情况下的平面高程几何精度,标志着中国几何高精度卫星载荷平台研制水平和地面处理水平达到了国际先进水平。资源三号测绘卫星是国产卫星有过去几何定性到高精度定量的里程碑,有着广阔的应用前景。
致 谢:感谢黑龙江省测绘地理信息局测量了大连区域的GPS点;感谢北京吉威数源信息技术有限公司、中国测绘科学技术研究院和航天五院503所在软件方面的支持。
| [1] | DIAL G F,BOWEN H,GERLACH B,et al.IKONOS Satellite,Sensor,Imagery,and Products[J].Remote Sensing of Environment,2004,88(1-2):23-36. |
| [2] | Digital Globe.DigitalGlobe Core Imagery Products Guide.[EB/OL].[2012-01-01].http://www.digitalglobe.com/digitalglobe2/file.php/811/DigitalGlobe_Core_Imagery_Products_Guide.pdf. |
| [3] | De VALENCIA K J,PAREDES Jr F,WALKER A S.Rigorous Sensor Modeling and Triangulation for Orbview-3[EB/OL].[2012-01-01].http://www.asprs.org/a/publications/proceedings/reno2006/0030.pdf. |
| [4] | ZHANG L,GRUEN A.Multi-image Matching for DSM Generation from IKONOS Imagery[J].ISPRS Journal of Photogrammetry and Remote Sensing,2006,60(3):195-211. |
| [5] | De LUSSY F,KUBIK P,GRESLOU D,et al.Pleiades-HR Image System Products and Quality Pleiades-HR Image System Products and Geometric Accuracy[EB/OL].[2012-01-01].http://cmsv021.rrzn.uni-hannover.de/fileadmin/institut/pdf/075-delussy.pdf. |
| [6] | GAEL Consultant.SPOT 123-4-5 Geometry Handbook[EB/OL].[2012-01-01].http://www-igm.univ-mlv.fr/-riazano/publications/GAEL-P135-DOC-001-01-04.pdf. |
| [7] | ZHANG Guo.Rectification for High Resolution Remote Sensing Image Under Lack of Ground Control Points[D].Wuhan:Wuhan University,2005.(张过.缺少控制点的高分辨率卫星遥感影像的几何纠正[D].武汉:武汉大学,2005.) |
| [8] | ZHU Xiaoyong,ZHANG Guo,TANG Xinming,et al.Research and Application of CBRS02B Image Geometric Exterior Calibration[J].Geography and Geo-information Science,2009,25(3):16-18.(祝小勇,张过,唐新明,等.资源一号02B卫星影像几何外检校研究及应用[J].地理与地理信息科学,2009,25(3):16-18.) |
| [9] | OGC (OpenGIS Consortium).The OpenGIS Abstract Specification,Topic 7:the Earth Imagery Case[EB/OL].[2012-01-01].http://www.opengis.org/public/abstract/99-107.pdf. |
| [10] | TAO V C,HU Yong.A Comprehensive Study of the Rational Function Model for Photogrammetric Processing[J].Photogrammetric Engineering and Remote Sensing,2001,67(12):1347-1357. |
| [11] | GRODECKI J,DIAL G.Block Adjustment of High-resolution Satellite Images Described by Rational Polynomials[J].Photogrammetric Engineering and Remote Sensing,2003,69:59-68. |
| [12] | DIAL G,BOWEN H,GERLACH F,et al.IKONOS Satellite,Imagery,and Products[J].Remote Sensing of Environment,2003,88(1-2):23-36. |
| [13] | FASER C S,HANLEY H B.Bias-compensated RPCs for Sensor Orientation of High-resolution Satellite Imagery[J].Photogrammetric Engineering and Remote Sensing,2005,71(8):909-915. |
| [14] | ZHANG Guo,LI Deren,YUAN Xiuxiao,et al.The Mapping Accuracy of Satellite Imagery Block Adjustment[J].Journal of Zhengzhou Institute of Surveying and Mapping,2006,23(4):239-241.(张过,李德仁,袁修孝,等.卫星遥感影像的区域网平差成图精度[J].测绘科学技术学报,2006,23(4):239-241.) |
| [15] | LI Deren,ZHANG Guo,JIANG Wanshou,et al.SPOT-5 HRS Satellite Imagery Block Adjustment without GCPS or with Single GCP[J].Geomatics and Information Science of Wuhan University,2006,31(5):377-381.(李德仁,张过,江万寿,等.缺少控制点的SPOT-5 HRS影像RPC模型区域网平差[J].武汉大学学报:信息科学版,2006,31(5):377-381.) |
| [16] | ZHANG Guo,LI Zhen,PAN Hongbo,et al.Orientation of Spaceborne SAR Stereo Pairs Employing the RPC Adjustment Model[J].IEEE Transactions on Geoscience and Remote Sensing,2011,49(7):2782-2792. |
| [17] | JIANG Wanshou.Multiple Aerial Image Matching and Automatic Building Detection[D].Wuhan:Wuhan University,2004.(江万寿.航空影像多视匹配与规则建筑物自动提取方法研究[D].武汉:武汉大学,2004.) |
| [18] | ZHANG Li,ZHANG Jixian.Multi-image Matching for DEM Generation from Satellite Imagery[J].Science of Surveying and Mapping,2008,(S2):35-39.(张力,张继贤.基于多基线影像匹配的高分辨率遥感影像DEM自动生成[J].测绘科学,2008,(S2):35-39.) |
| [19] | ZHANG Guo,CHEN Tan,PAN Hongbo,et al.Patch-based Least Squares Image Matching Based on Rational Polynomial Coefficients Model[J].Acta Geodaetica et Cartographica Sinica,2011,40(5):592-597.(张过,陈钽,潘红播,等.基于有理多项式系数模型的物方面元最小二乘匹配[J].测绘学报,2011,40(5):592-597.) |