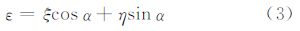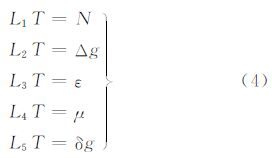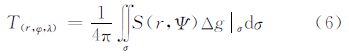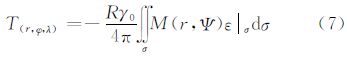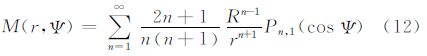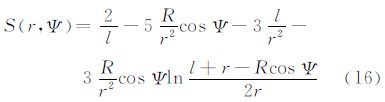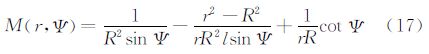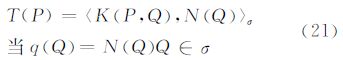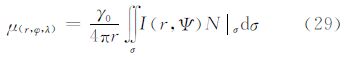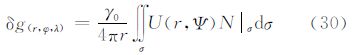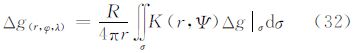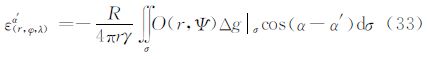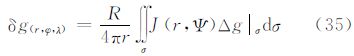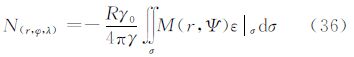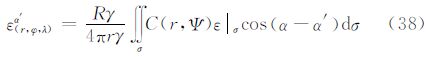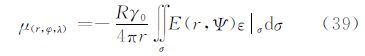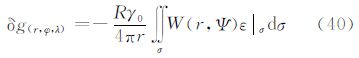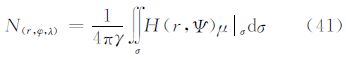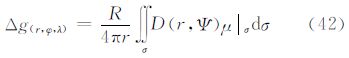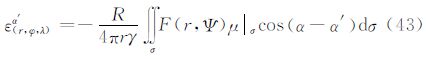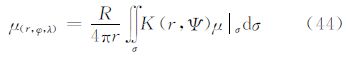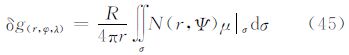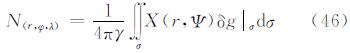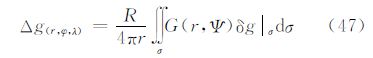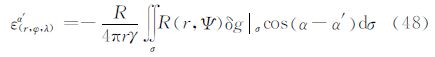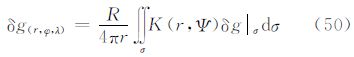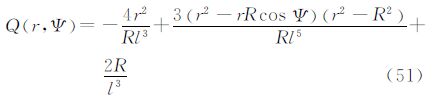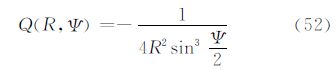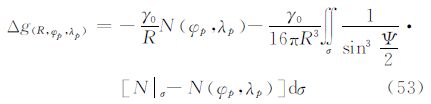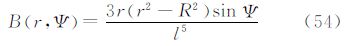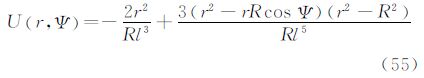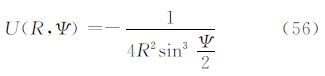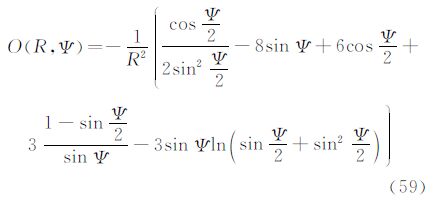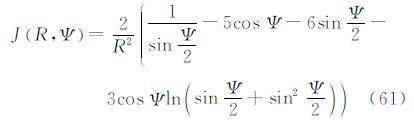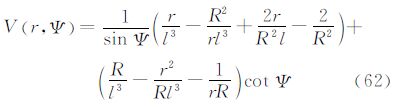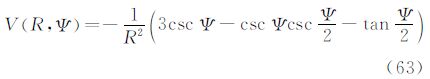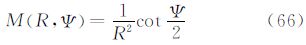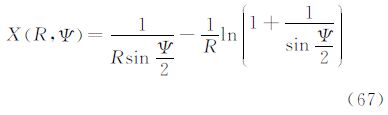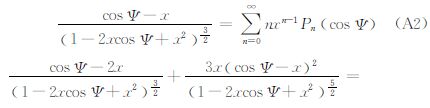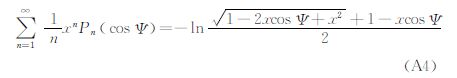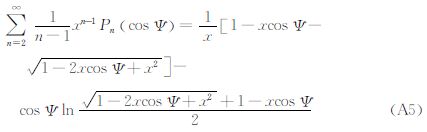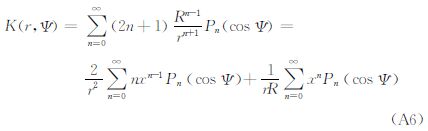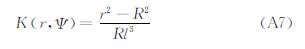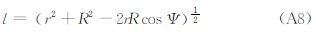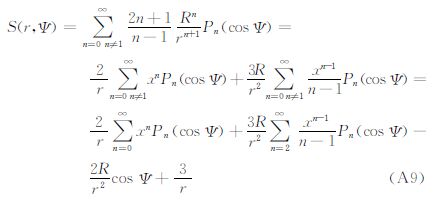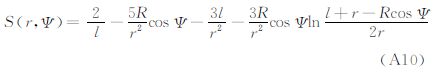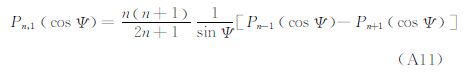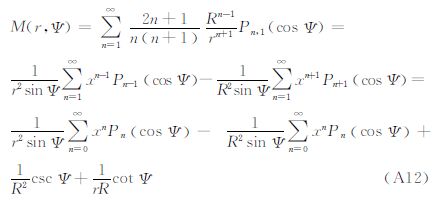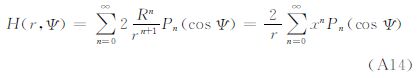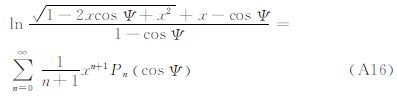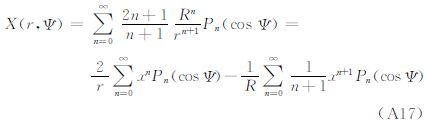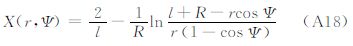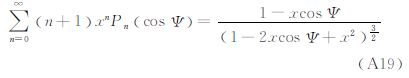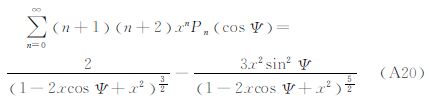1 引 言
地球形状与地球重力场是物理大地测量学的主要研究任务[1]。重力异常Δg、大地水准面高N、垂线偏差ε等扰动场元是地球内部物质分布与运动在地球表面或/和外部空间的物理表现。研究地球内部密度分布与结构的手段之一是利用地表上表征地球重力场特征的物理测量数据通过空域或频域的反演予以解释和描述[2]。
由大地水准面上的重力异常推求大地水准面在正常椭球面上的高的计算关系可由Stokes公式[3]表达;由大地水准面上的重力异常求解垂线偏差的子午分量和卯酉分量的计算关系可由Vening-Meinesz公式[4]表达;文献[5, 11]给出了由地表垂线偏差推求大地水准面高的计算方法;逆Vening-Meinesz公式[6, 11]给出了由地表垂线偏差推求重力异常的计算方法;逆Stokes公式[7, 8]给出了由大地水准面高推求重力异常的计算方法;根据球的第3外部边值问题,Bjerhammar公式[7]建立了由地球内部一个虚拟球面上的重力异常研究地球形状及外部重力场的关系;Hotine公式[9]导出了扰动重力与大地水准面高的基本关系式。文献[10]根据引力位的等值层原理建立了虚拟点质量模型。文献[12]给出了利用虚拟单层密度确定扰动重力的方法;文献[13, 14]在球近似条件下给出了重力异常、虚拟单层密度之间相互计算的公式,利用算子运算关系导出了广义逆Stokes公式、广义逆Vening-Meinesz公式和广义Molodensky公式。以上各种不同反演方法以及各自独特的推导过程从不同角度描述和剖析了物理大地测量学的研究内容以及相应理论。
本文根据核函数的一阶边界算子定义的方法,尝试在统一的核函数变换框架下,构造扰动场元间相互换算的关系,补充和完善上述相关公式。相对一阶边界算子定义而言,通过核函数变换可以扩展对经典公式的理解和认识,给出不仅局限于在大地水准面上应用的公式,而且可以获得计算地球外部任意点的扰动场元公式。基于二阶边界算子定义的重力梯度扰动场元随着GOCE卫星发射[15]也成为反演地球重力场的重要数据[16, 17, 18]。对于二阶边界算子定义的扰动场元变换理论在另外一文中给出详细过程。
2 物理大地测量边值问题及算子定义 2.1 边值问题描述扰动场元的计算实质上是寻求一种场转换器,其输入信号为地表重力场场元的观测值以及由卫星或卫星-地面联合得到的重力场有限阶谱等,输出信号为所需要的某一特定的扰动场元。通过某种线性化手段,寻求场转换器的问题归结为解物理大地测量边值问题[1]
式中,T为扰动位;∑为边值问题的边界面,称为正常地球表面,或似地球表面;Ω为以∑为边界面的外部空间开集;L为边界算子,是一种运算关系,把扰动场的基元T映射成边界函数q,其中的q可以是重力异常Δg,单层密度μ,大地水准面高N,垂线偏差ε,扰动重力δg等扰动场元。 2.2 算子定义在物理大地测量中,根据重力位W、正常重力位U和扰动位T之间的相互关系以及大地水准面高N、重力异常Δg、垂线偏差ε、单层密度μ、扰动重力δg的定义,在球面边界条件下,上述几个量之间的函数关系式为
式中,γ为正常重力;r为地心距;R为边界面球的半径;Ψ为球面上任意方向的球面角距。在式(2)中,第1项是著名的Bruns公式[19];第2项称为物理大地测量基本微分方程[20];第3项是根据垂线偏差的定义,在α方向上的垂线偏差表示,与垂线偏差在子午圈和卯酉圈方向的分量(ξ,η)的关系为 式中,α为由北子午线方向起算至Ψ方向的方位角;第4项的单层密度是重力异常Δg与大地水准面高N的组合;第5项是卫星重力测量技术中一个很重要的观测量。上述表达式给出了大地水准面高N、重力异常Δg、垂线偏差ε、单层密度μ、扰动重力δg与重力场扰动位T之间的关系,可表示为扰动位的泛函。在此,把式(2)表示为算子运算的形式 式中,L1、L2、L3、L4、L5定义为算子符号。 3 边值问题的延拓解当只研究地球外部空间扰动位时,根据球的外部边值问题的解[20],可以得到
式中,(r,φ,λ)为求值点;N|σ 、Δg|σ 、ε|σ 、μ|σ 、δg|σ 分别为边界面上的函数;γ0为边界面上的正常重力;K(r,Ψ)、S(r,Ψ)、M(r,Ψ)、H(r,Ψ)、X(r,Ψ)分别为式(2)边值条件下的扰动位的Laplace方程解的核函数。其相应的Legendre函数级数的表达式分别如下各Legendre函数级数的封闭表达式分别为
其中 式中,核函数K(r,Ψ)为Poisson核。式(5)的积分称为Poisson积分[1];式(6)是Stokes积分[3],S(r,Ψ)为相应的核函数;式(7)中的M(r,Ψ)是方向变化积分公式[13]中的核函数;式(8)中的H(r,Ψ)是Hotin公式[8]中的核函数;在文献[20]中给出了式(9)核函数X(r,Ψ)的详细推导过程。上述各公式可以用统一的形式表示为 4 核函数变换 4.1 K(r,Ψ)函数变换根据式(5)的外部边值问题的解,结合式(4)定义的算子运算,可以计算与之相对应的扰动场元。顾及球谐函数的正交性[1, 21],可以得到
式中,ε(r,φ,λ)α′为计算点(r,φ,λ)处沿方位角α′方向的垂线偏差,ε(r,φ,λ)α′=ξcos α′+ηsin α′。Q(r,Ψ)、B(r,Ψ)、I(r,Ψ)、U(r,Ψ)为相应积分核函数。 4.2 S(r,Ψ)函数变换同理,根据式(6)的外部边值问题的解,可以得到
式中,O(r,Ψ)、Z(r,Ψ)、J(r,Ψ)为相应积分核函数。 4.3 M(r,Ψ)函数变换同理,根据式(7)的外部边值问题的解,可以得到
式中,V(r,Ψ)、C(r,Ψ)、E(r,Ψ)、W(r,Ψ)为相应积分核函数。 4.4 H(r,Ψ)函数变换同理,根据式(8)的外部边值问题的解,可以得到
式中,D(r,Ψ)、F(r,Ψ)、N(r,Ψ)为相应积分核函数。 4.5 X(r,Ψ)函数变换同理,根据式(9)的外部边值问题的解,可以得到
式中,G(r,Ψ)、R(r,Ψ)、P(r,Ψ)为相应积分核函数。 5 几个重要的积分公式讨论相对经典物理大地测量公式应用的边界面条件,本文把含有因子r的对应扰动场元反演关系的公式称为广义积分公式。本节重点讨论其中一些广义积分公式,以及与相应经典公式之间的演化过程。
5.1 由大地水准面高计算重力异常广义公式由式(4)定义的算子L2可将扰动位映射为重力异常。通过式(5)得到式(27)。其中,核函数Q(r,Ψ)的封闭表达式为
利用式(27)及式(51)可以由边界面上的大地水准面高计算边界面外的重力异常。当边界面为大地水准面,且仅计算大地水准面上的重力异常时,即r=R时,由于核函数Q(r,Ψ)在Ψ=0处奇异,还需作简单的变换。将式(27)的积分分为两部分,一部分定义在Ψ=0处,即点(φp,λp)处,此处大地水准面高为N(φp,λp);另一部分定义在Ψ≠0区域。利用Q(R,Ψ)的无穷级数形式可以推导得到其封闭表达式为
并且在Ψ=0处利用Legendre函数的正交性,最后得到 式(53)为经典的逆Stokes公式[7, 8]。说明当r=R时,式(27)可退化为经典的逆Stokes公式。 5.2 由大地水准面高计算垂线偏差广义公式通过算子L3,可以将扰动位换算为垂线偏差ε。将算子L3应用于式(5)得到利用边界面上的大地水准面高N计算边界面外的垂线偏差ε的式(28)。其中,核函数B(r,Ψ)的封闭表达式为
利用式(28)及式(54)可以计算边界面外任意点的垂线偏差,它也是文献[5, 11]给出扰动场元关系的逆运算。
5.3 由大地水准面高计算扰动重力广义公式利用算子L5的定义,可以将任意一点的扰动位映射为扰动重力。通过式(5)可以得到利用边界面上的大地水准面高N计算边界面外的扰动重力δg的式(30)。其中,核函数U(r,Ψ)的封闭表达式为
利用式(30)及式(55)即可以计算边界面外的扰动重力δg,也可以计算边界面上扰动重力δg。对于边界面外的扰动重力δg计算,核函数U(r,Ψ)在任何点处都没有奇异性。当仅需要计算边界面上扰动重力δg时,即当r=R时,核函数U(R,Ψ)在Ψ=0处奇异。与5.1节处理过程一样,在Ψ=0处,应用核函数U(R,Ψ)的无穷级数表达式;在Ψ≠0区域,应用核函数U(R,Ψ)的封闭表达式
最后得到边界面上扰动重力δg的计算公式为
比较文献[9],式(30)是Hotine公式的逆运算。当精密定位技术广泛应用于地面重力测量、航空重力测量以及卫星重力测量业务中,利用大地水准面高确定/检核空间扰动重力或地表扰动重力将发挥重要作用。
5.4 由重力异常计算垂线偏差广义公式根据算子L3的定义,将L3作用于式(6)得到由重力异常Δg计算垂线偏差ε的公式(33)式。其中,核函数O(r,Ψ)的封闭表达式为
利用式(33)和式(58)可以由大地水准面上的重力异常Δg计算大地水准面外的垂线偏差ε。如果令式(58)中的r=R,得到
式(59)称为Vening-Meinesz函数。这时,式(33)退化为经典的Vening-Meinesz公式[4]。
5.5 由重力异常计算扰动重力广义公式利用算子L5,作用于式(6),可以得到式(35)。其中,核函数J(r,Ψ)的封闭表达式为
利用式(35)和式(60)可以由大地水准面上的重力异常计算外部的扰动重力。如前所述,当精密定位技术广泛应用于物理大地测量的实际观测中,获得扰动重力变得越来越可行。因此,建立两者之间的关系在今后的应用也越来越重要。当重力异常与扰动重力处于同一边界面时,核函数J(R,Ψ)为
5.6 由垂线偏差计算重力异常广义公式同样,由式(4)定义的算子运算,将算子L2作用于式(7)得到式(37)。其中,核函数V(r,Ψ)的封闭表达式为
当仅计算边界面上的重力异常,且边界面定义为大地水准面时,令式(37)中的r=R,核函数V(r,Ψ)的表达式简化为
与文献[6]给出的逆Vening-Meinesz公式比较,两者完全一致,说明广义公式在r=R时可演化为经典逆Vening-Meinesz公式。
5.7 由垂线偏差计算扰动重力广义公式根据算子L5的定义,并将算子L5应用于式(7),可以得到计算扰动重力的公式式(40)。其中,核函数W(r,Ψ)的封闭表达式为
利用式(40)以及式(64)的核函数形式就可以由边界面上的垂线偏差计算边界面外的扰动重力。同样,对于边界面上的扰动重力计算,仍是令式(40)中的r=R,此时核函数W(r,Ψ)的表达式为
在卫星测高技术中,利用测高卫星沿迹的海面高(SSH)观测值可以得到海面梯度(SSG)的信息,在扣除海面相对大地水准面的倾斜后(在几千平方公里范围内),可以得到该局部海域的垂线偏差观测值。因此,在确定海洋区域的地球重力场中,除了利用垂线偏差确定大地水准面高[5, 11]或重力异常[6]外,式(40)将扩展垂线偏差观测值的应用范围。
5.8 由垂线偏差计算大地水准面高广义公式将算子L1应用于式(7),可以得到大地水准面高N的计算公式式(36)。当边界面定义为大地水准面,且仅在边界面上计算时,令式(36)中的r=R,核函数M(R,Ψ)的表达式为
此时,式(36)演化为与文献[5]中完全一致的公式。但与文献[11]比较,式(66)的核函数M(R,Ψ)与该文献给出的核函数C(Ψ)略有差异,主要区别在于两者的核函数级数求和的起始项不同。
5.9 由扰动重力计算大地水准面高广义公式根据式(4)对算子L1规定的运算,通过式(9)得到式(46)。由式(14)或式(19)表达的核函数X(r,Ψ)通过式(46)的积分计算就可以得到大地水准面高。当扰动重力δg分布在大地水准面上时,此时的核函数
式(67)与经典的Hotine公式[9]中的核函数表达式不完全一致,主要区别仍然是无穷级数求和的起始项不同所造成的差异。根据正常椭球质量和真实地球总质量相同的假设以及对正常椭球定位的约束,扰动位不存在零阶项、一阶项,则扰动重力也不存在零阶项、一阶项。由于广义公式与经典公式中的核函数区别就在于两者相差了无穷级数求和的零阶项和一阶项,根据面球谐函数的正交性,利用式(46)及式(67)计算的大地水准面高与经典Hotine公式的计算结果没有区别,但经典的Hotine公式要求大地水准面高和扰动重力必须处于同一边界面。
6 核函数与外部扰动场元映射关系表重力异常Δg、单层密度μ、大地水准面高N、垂线偏差ε、扰动重力δg等均是扰动位T的泛函。通过扰动位T与其他扰动场元的泛函关系,可以得到扰动场元之间的相互换算公式。其核函数与外部扰动场元映射的关系如表 1所示。
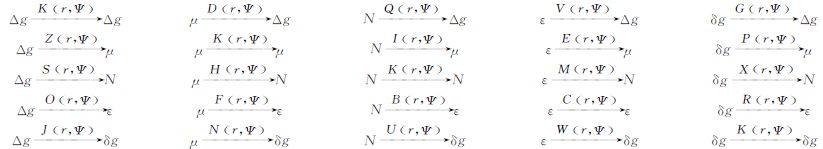 |
表 1给出了所列扰动场元之间的换算关系。除了上一节给出的9个广义积分公式外,表 1第一行第一列(以下用表(1,1)表示)公式,当地球内部重力异常定义为虚拟球面上的重力异常,则该公式表现为Bjerhammar公式形式;表(3,1)公式是Stokes公式形式;表(1,2)公式是虚拟点质量模型公式形式;表(2,2)公式是虚拟单层密度模型公式形式。表 1中有些关系式已有明确的应用背景,还有些关系式需要在实际物理大地测量中挖掘其应用价值,探索可能产生新的技术途径。
7 结 论(1) 在扰动场元之间的换算中,由于没有限定扰动场元在同一个参考面上,因此,本文给出的公式更具一般性。除了用垂线偏差计算其他扰动场元的公式之外,所涉及的核函数当r≠R时均不存在奇异性。但当相互换算的扰动场元定义在同一个参考面上时,有些核函数在Ψ=0时变为奇异。实际应用中,上述积分表达式计算均以离散化方式完成,而Ψ=0时的内环带影响的计算方法可参见文献[11]。
(2) 在表 1中共出现22个核函数。有些核函数的表达式与经典公式中的形式完全一致,表明了它们是经典公式的再现。有些核函数的形式需要投影到边界面上才与经典公式相一致,说明了广义公式与经典公式之间的内在联系。还有个别核函数由于级数求和形式下的起始项不同,导致核函数封闭表达式存在差异,但在实际计算过程中并不会产生影响。
(3) 本文推导的公式均包含了因子r,给出的公式不仅限于在大地水准面上应用,而且可以计算地球外部任意点的扰动场元。
附录:有关核函数封闭形式的推导根据Legendre多项式的母函数
当x<1时,式(A1)的级数绝对、一致地收敛。由式(A1)还可以得到另外,根据文献[22],有
在式(A1)、式(A2)、式(A3)、式(A4)、式(A5)中,令x= 。由于
。由于
将式(A1)、式(A2)代入式(A6),整理可得
式中另
将式(A1)、式(A5)代入式(A9),整理可得
再根据Legendre函数递推公式
则将式(A1)代入式(A12),整理可得
另
将式(A1)代入式(A14),整理可得
由式(A1)还可得
则将式(A1)、式(A16)代入式(A17),整理可得
由式(A1)还可得
由式(A19)可得
由式(A2)可得
按照如上的推导思路,其他核函数的封闭表达式可以分别获得,不再逐一列出。
| [1] | HEISKANEN W A, MORITZ H. Physical Geodesy[M]. San Francisco: Freeman W H and Company, 1967. |
| [2] | NEREM R S, JEKELI C, KAULA W M. Gravity Field Determination and Characteristics: Retrospective and Prospective[J]. Journal of Geophysical Research, 1995,100(B8): 15053-15074. |
| [3] | STOKES G G. On the Variation of Gravity on the Surface of the Earth[J]. Transactions of the Cambridge Philosophical Society, 1849, 8: 672-695. |
| [4] | VENING-MEINESZ F A. A Formula Expressing the Deflection of the Plumb-lines in the Gravity Anomalies and Some Formulae for the Gravity Field and the Gravity Potential Outside the Geoid[J]. Proceedings of the Koninklijke Nederlandse Academie van Wetenschappen, 1928,31(3):315-331. |
| [5] | MOLODENSKY M S, EREMEEV V F, YOURKINA M I. An Evaluation of Accuracy of Stokes’ Series and of Some Attempts to Improve His Theory[J]. Bulletin Géodésique, 1962, 63(1): 19-37. |
| [6] | MOLODENSKY M S, EREMEEV V F, YOURKINA M I. Methods for Study of the External Gravitational Field and Figure of the Earth Works of Central Research Institute of Geodesy Aerial Photography and Cartography[M]. Moscow: Geodetic Literature Press, 1960. |
| [7] | BJERHAMMAR A. A New Theory of Geodetic Gravity[M]. Stockholm: Tekniska hgskolan, 1964. |
| [8] | MORITZ H. Advanced Physical Geodesy[M]. England: Abacus Press, 1980. |
| [9] | HOTINE M. Mathematical Geodesy[M]. Washington DC: U S Environmental Science Services Administration, 1969. |
| [10] | PAUL E N. The Formation and Evaluation of Detailed Geopotential Models Based on Point Masses[R]. Columbus:Ohio State University, 1970. |
| [11] | HWANG C. Inverse Vening-Meinesz Formula and Deflection-geoid Formula: Application to the Predictions of Gravity and Geoid over the South China Sea[J]. Journal of Geodesy, 1998, 72(5): 304-312. |
| [12] | XU Houze,ZHU Zhuowen. The Expression of the Suppositional Single Layer Density of the Exterior Gravity Field[J]. Science in China: Series B,1984(6): 575-580. (许厚泽,朱灼文. 地球外部重力场的虚拟单层密度表示[J]. 中国科学: B辑,1984(6): 575-580.) |
| [13] | CHENG Luying, XU Houze. Disturbance Gravitational Computation Methods Comparison[J]. Journal of Institute of Surveying and Mapping, 2003, 20(3): 161-164. (程芦颖, 许厚泽. 外空扰动引力计算方法的内在联系[J]. 测绘学院学报, 2003, 20(3): 161-164.) |
| [14] | CHENG L Y. HSU H T. General Inverse of Stokes, Vening-Meinesz and Molodensky Formulae[J]. Science in China: Earth Sciences, 2006, 49(5): 499-504. |
| [15] | European Space Agency. ESA’s Gravity Mission GOCE[EB/OL].[2010-03-20]. http://www.esa.int/ living-planet /goce. |
| [16] | GRUBER T, RUMMEL R, KOOP R. How to Use GOCE Level 2 Products[C]// Proceedings of the 3rd International GOCE User Workshop. Frascati: ESA-ESRIN, 2007: 205-211. |
| [17] | ZHANG Chuanding, LU Zhonglian, WU Xiaoping. Generalized Spherical Harmonic Functions and Its Applications on the BVPs of Gravity Gradients[J]. Acta Geodaetica et Cartographica Sinica, 1998, 27(3): 252-258. (张传定,陆仲连,吴晓平. 广义球谐函数及其在重力梯度边值问题中的应用[J]. 测绘学报, 1998, 27(3): 252-258.) |
| [18] | WU Xing, ZHANG Chuanding, WANG Kai. Point-mass Harmonic Analysis of Satellite Gradiometry Boundary Value Problem[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 213-219. (吴星,张传定,王凯. 卫星重力梯度边值问题的点质量调和分析[J]. 测绘学报,2011, 40(2): 213-219.) |
| [19] | BRUNS H. Die Figur der Erde[M]. Berlin: Druck und Verlag von P. Stankiewicz′uch Druckerei, 1878. |
| [20] | LU Zhonglian. The Theory and Method of the Earth Gravity Field[M]. Beijing: Press of PLA, 1996. (陆仲连. 地球重力场理论与方法[M]. 北京: 解放军出版社, 1996.) |
| [21] | GUO Junyi. Foundation of Physical Geodesy[M]. Wuhan: Press of Wuhan Technical University of Surveying and Mapping, 1994. (郭俊义. 物理大地测量学基础[M]. 武汉:武汉测绘科技大学出版社,1994.) |
| [22] | GRADSHTEYN I S. RYZHIK I M. Table of Integrals, Series, and Products[M]. Boston: Academic Press, 1994. |