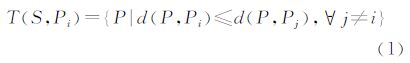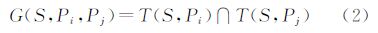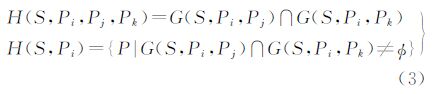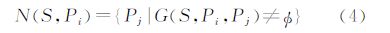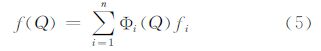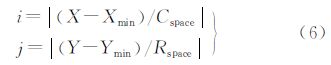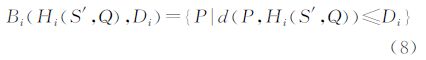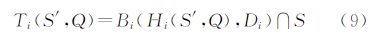2. 海军大连舰艇学院 海洋测绘工程军队重点实验室,辽宁 大连 116018
2. Key Laboratory of Hydrographic Surveying and Mapping of PLA, Dalian Naval Academy, Dalian 116018, China
1 引 言
格网数字水深模型(grid digital depth model,Grid-DDM)是区域海底表面的矩阵式数字化表达,是反映海洋水深变化的常用模型[1]。高质量的Grid-DDM构建,在舰船海上航行、海洋工程建设、海底勘探、军事活动等应用领域都具有重要意义[1]。相关研究[2, 3, 4]表明,为了满足高质量Grid-DDM构建要求,其数据源多采用具有较强局部相关性的高分辨率、海量多波束测深数据;而为了提高基于多波束测深数据的Grid-DDM建模效率,其插值方法普遍采用了局部插值的方法(local method)。所谓局部插值,是指某一点的插值应该主要取决于其附近区域的结点,而不是较远处甚至整个区域的结点[3, 4]。
Voronoi图是表示离散空间数据点空间相邻性的一种常用数学方法,在空间离散点插值方面有着广泛的应用[5]。基于Voronoi图的逐点内插算法称为自然邻点插值(natural neighbor interpolation,NNI)[6]。该算法以计算几何为理论基础,充分体现了Voronoi单胞和Delaunay三角形的几何特性,准确表达了离散数据间的局部相关性[7, 8]。其特点更适用于以多波束测深数据为数据源的包含复杂海底地形(如断崖、海底火山、礁岩、冲槽等)的Grid-DDM构建[6, 9]。但是,由于传统的NNI算法需要生成全局Voronoi图,从而造成算法的效率极其低下,严重影响了NNI算法的实际应用[10, 11]。为提高算法的效率,当前较为普遍的一种做法是通过生成局部动态Voronoi图近似代替全局Voronoi图来提高NNI算法效率[12, 13, 14],但这种简单的近似代替却造成了算法精度的丢失。
为克服传统NNI算法的不足,依据Voronoi单胞和Delaunay三角形的几何特性,提出一种基于局部动态最优Voronoi图的NNI算法,并在VC++环境下结合多波束测深数据对其在Grid-DDM中的应用进行了验证。试验结果表明该算法具有执行效率高、插值精度不丢失等优点。
2 传统NNI算法及其存在问题 2.1 Voronoi单胞和Delaunay三角形自提出NNI算法提出以来,以Voronoi图为几何基础的数值算法在国内外得到了极大关注。Voronoi图是一种常用的非结构化网格,它所剖分的每一个网格单元被称为Voronoi单胞。Voronoi单胞在任意n维度空间的数学描述为[2, 10, 15]:
设Ω是任意维度空间Rn上的凸空间,令S={P1,P2,…,PN}为Ω内分布的有限离散点集,且当i≠j时,Pi≠Pj。任取离散点Pi、Pj作其垂直平分线,将平面分成两个分别包含离散点Pi、Pj的半平面。包含离散点Pi所有半平面的交集组成一个封闭或无界的凸多边形,该凸多边形构成了离散点Pi的一个子空间T(S,Pi),且满足
式中,P表示子空间T(S,Pi)内任意一点,即P∈T(S,Pi);d(P,Pi)、d(P,Pj)分别表示点P至离散点Pi、Pj的距离;子空间T(S,Pi)即为离散点Pi的Voronoi单胞。显然Pi∈T(S,Pi),从而给定Ω中的有限离散点集S,即可唯一确定任意离散点Pi在Ω中的Voronoi单胞T(S,Pi)。在式(1)基础上,Voronoi边定义为任意两个Voronoi单胞的公共边界[12, 16],即
式中,G(S,Pi,Pj)表示S中离散点Pi所在的子空间(Voronoi单胞)T(S,Pi)与离散点Pj所在的子空间(Voronoi单胞)T(S,Pj)的交集。基于式(2),Voronoi顶点的数学定义如下
式中,H(S,Pi,Pj,Pk)表示S中离散点Pi的两条Voronoi单胞公共边界(Voronoi边)G(S,Pi,Pj)、G(S,Pi,Pk)的交集;H(S,Pi)表示S中离散点Pi的Voronoi顶点集。
如图 1所示,对于任意Voronoi顶点H(S,Pi,Pj,Pk)而言,其至Voronoi边G(S,Pi,Pj)、G(S,Pi,Pk)对应的离散点Pi、Pj、Pk的距离相等。顺次连接离散点Pi、Pj、Pk所得到的三角形,称为Delaunay三角形[17, 18, 19]。由Delaunay三角形的空外接圆特性可知,以Voronoi单胞T(S,Pi)上任意Voronoi顶点H(S,Pi,Pj,Pk)为圆心,以H(S,Pi,Pj,Pk)至离散点Pi的距离为半径的圆与有限离散点集S的交集为∅。

|
| 图 1 Voronoi单胞和Delaunay三角形 Fig. 1 Voronoi cells and Delaunay triangles |
NNI算法是以Voronoi图为几何基础的数值算法。该算法主要依据自然邻点(natural neighbors,NN)的概念构建,所谓自然邻点是指包含离散点的Voronoi单胞相邻的Voronoi单胞所包含的离散点[10, 21]。即
式中,N(S,Pi)表示有限离散点集S中离散点Pi的自然邻点集;离散点Pj表示离散点Pi的任意自然邻点;G(S,Pi,Pj)表示离散点Pi的任意Voronoi边。自然邻点的重要性在于其定义了几何特性上距离某离散点Pi的最近离散点集N(S,Pi),且N(S,Pi)的数目和位置唯一地取决于有限离散点集S在离散点Pi处的局部分布。对于有限离散点集S中任意离散点Pi而言,其Voronoi顶点集H(S,Pi)与其自然邻点集N(S,Pi)具有等价性[14, 22]。如图 1所示,自然邻点集N(S,Pi)中各自然邻点与离散点Pi同样满足Delaunay三角形的空外接圆特性。
传统NNI算法在不破坏有限离散点集S空间拓扑关系的前提下,依据式(4)通过生成全局Voronoi图获取待插点Q的自然邻点集N(S,Q),并根据N(S,Q)中各自然邻点对待插点Q的形函数值Φi(Q)的贡献率来计算待插点Q的插值结果,由此可构造插值函数
式中,f(Q)表示待插点Q的物理量值;n表示待插点Q的自然邻点数;fi表示第i个自然邻点的物理量值;Φi(Q)表示第i个自然邻点的插值形函数在待插点Q处的值,常用的Φi(Q)有Sibson插值和Laplace插值两种[12, 16]。
2.3 传统NNI存在的主要问题由2.2节中传统NNI算法构建原理可知,待插点Q的插值精度取决于自然邻点集N(S,Q)的正确生成。对于数据量较小的有限离散点集S,可依据式(4)通过生成全局Voronoi图直接获取待插点Q的自然邻点集N(S,Q)[6, 10]。然而对于数据量较大(海量)的有限离散点集S(如多波束测深数据),这种基于全局Voronoi图的自然邻点集N(S,Q)生成算法效率则严重降低,甚至无法执行[2, 20]。
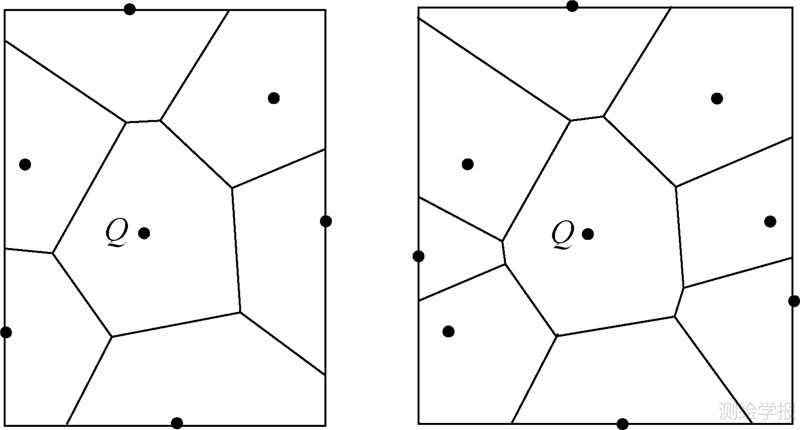
为提高算法的效率,文献[12, 14]提出了一种基于局部动态Voronoi图的自然邻点集的获取算法,该类算法依据距离待插点Q越远的离散点对于插值结果影响越小的原理(如以待插点Q为中心,给定缓冲距为半径)搜索满足一定数量特征的局部离散点集S′(S′⊆S),在此基础上以局部离散点集S′代替有限离散点集S,并依据式(4)通过生成局部Voronoi图获取待插点Q的自然邻点集N(S′,Q),但由于无法保证N(S′,Q)与N(S,Q)的等价性。这类算法尽管提高了算法的执行效率,却是以牺牲待插点的精度为代价的。如图 2所示,在局部离散点集S′不同的情况下,待插点Q的自然邻点集N(S′,Q)亦不同。
|
| 图 2 不同局部离散点集下待插点的自然邻点集 Fig. 2 Interpolated point’s natural neighbors based on different local discrete point set |
由2.3节中的分析可知,基于局部动态Voronoi图的NNI算法尽管提高了算法的执行效率,却造成了插值精度的丢失。造成上述插值精度丢失的原因则是由于基于局部离散点集S′生成的自然邻点集N(S′,Q),仅在局部离散点集S′中满足Delaunay三角形的空外接圆特性,而在有限离散点集S中的Delaunay三角形的空外接圆特性则未加以考虑,从而无法保证N(S′,Q)与N(S,Q)的等价性。基于上述分析,本文提出一种局部动态最优Voronoi图的构建算法。所谓局部动态最优Voronoi图是指满足待插点Q在局部离散点集S′中的自然邻点集N(S′,Q)与其在有限离散点集S中的自然邻点集N(S,Q)等价的局部Voronoi图。局部动态最优Voronoi图的构建步骤如下。
3.1 空间索引数据建模针对数据量较大(海量)的有限离散点集S(如多波束测深数据),可对有限离散点集S进行格网化组织,即在确定索引格网的行宽(Rspace)与列宽(Cspace)的前提下,对每一个离散点,按照其空间位置的分布,计算其空间索引坐标[14, 20]。对于任意离散点Pi(X,Y,Z)∈S而言,其空间索引坐标值的计算公式为
式中,i、j分别表示空间索引块的行列号;Xmin、Ymin分别表示有限离散点集S在水平和垂直方向上的最小值。基于式(6),有限离散点集S被划分为(Cols-1)×(Rows-1)个索引格网数据块,即
式中,Cols、Rows分别表示索引格网的列数和行数;Sij表示有限离散点集S的任意索引格网数据块。
3.2 局部离散点集初始化局部离散点集初始化是在确定局部离散点集S′中初始离散点数M(M≥3)的前提下,依据待插点Q(X,Y,Z)的空间坐标,在有限离散点集S中寻找一定数量的索引格网数据块。
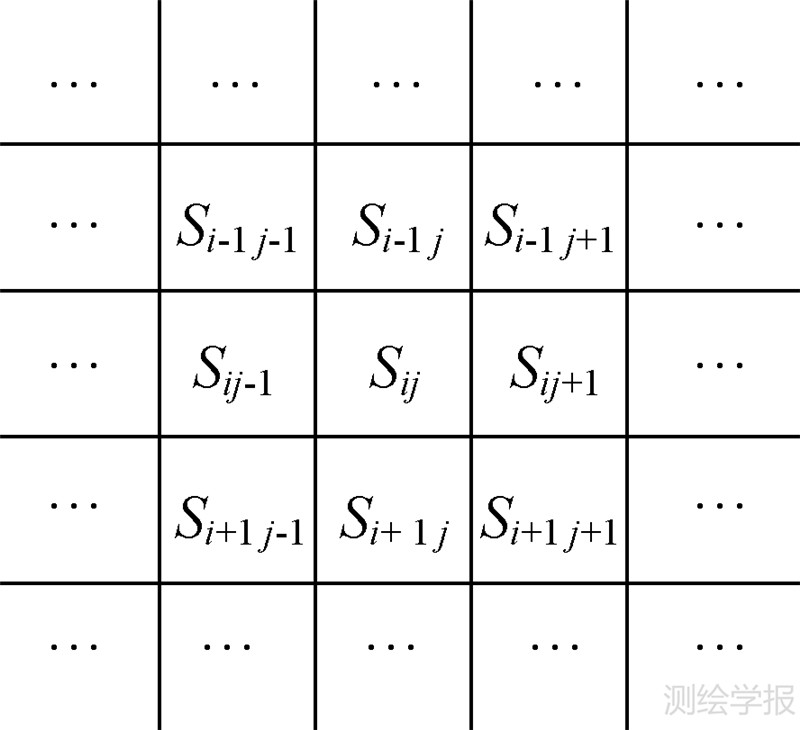
如图 3所示,依据式(6)计算待插点Q(X,Y,Z)所占的索引格网数据块Sij,并更新局部离散点集S′。若局部离散点集S′中离散点数目小于M,则对Sij进行八方向邻域搜索,即Si-1j-1、Si-1j、Si-1j+1、Sij-1、Sij+1、Si+1j-1、Si+1j、Si+1j+1,同时更新S′,直至S′中离散点数目大于等于M。
|
| 图 3 索引格网数据块示意图 Fig. 3 Sketch map of reference data block lattice |
依据2.1节中式(3)对于Voronoi顶点集的定义构建待插点Q在局部离散点集S′中的Voronoi顶点集H(S′,Q)。并以待插点Q的任意Voronoi顶点Hi(S′,Q)为圆心,Hi(S′,Q)至待插点Q的距离Di为半径作圆,形成圆形区域Bi(Hi(S′,Q),Di),即
基于式(8),对圆形区域Bi(Hi(S′,Q),Di)与有限离散点集S进行求交运算,形成临时点集Ti(S′,Q),即
在式(9)基础上,通过遍历待插点Q的Voronoi顶点集H(S′,Q),对所有临时点集Ti(S′,Q)进行求并运算,并最终形成点集T(S′,Q),即
式中,Num表示Voronoi顶点集H(S′,Q)的顶点数。
3.4 局部动态最优Voronoi图生成由2.2节中对于自然邻点的定义可知,待插点Q在局部离散点集S′中的Voronoi顶点集H(S′,Q)与其自然邻点集N(S′,Q)具有等价性,两者同时满足Delaunay三角形的空外接圆特性。据此可依据3.3节中Voronoi单胞最优化过程中生成的点集T(S′,Q)是否为∅来判断局部动态Voronoi图是否达到最优化(N(S′,Q)与N(S,Q)等价)的条件。
如图 4所示即为局部动态最优Voronoi图生成示意图,若点集T(S′,Q)=∅,则待插点Q在局部离散点集S′中的自然邻点集N(S′,Q)与其在有限离散点集S中的自然邻点集N(S,Q)等价;反之若点集T(S′,Q)≠∅,则更新局部离散点集S′=S′∪T(S′,Q),并重复步骤3.3,直至点集T(S′,Q)=∅。

|
| 图 4 局部动态最优Voronoi图生成示意图 Fig. 4 Sketch map of local dynamic optimal Voronoi diagram |
为验证算法的有效性,本文在VC++环境下实现了基于局部动态最优Voronoi图的NNI算法,并利用Surfer8.0软件对生成的试验结果进行了可视化显示与分析。试验采用的数据为我国东海某海区的多波束测深数据,共包含12 774个离散水深点,依据文献[14, 20]提供的经验参数,索引格网的行宽(Rspace)与列宽(Cspace)分别设置为1′,局部离散点集S′中初始离散点数M设置为25。Grid-DDM大小设置为100×87,插值形函数Φi(Q)选用Sibson插值。试验环境为Core(TM) i5处理器,主频为2.8 GHz,内存为2 GB。
试验共分3组,分别应用基于局部动态Voronoi图的NNI算法、基于全局Voronoi图的NNI算法以及本文提出的基于局部动态最优Voronoi图的NNI算法对试验数据进行了Grid-DDM的插值解算。图 5、图 6分别为基于上述不同NNI算法的等深线(等深距为5 m)及海底地形表面的对比图。从图中不难看出,基于局部动态Voronoi图的NNI算法所生成的Grid-DDM由于无法保证N(S′,Q)与N(S,Q)的等价性,从而造成了其在海底地形表达上的精度丢失。而本文提出的基于局部动态最优Voronoi图的NNI算法则从Voronoi单胞最优化构建的原理出发,保证了N(S′,Q)与N(S,Q)的等价性,从而其等深线图及海底地形表面图均与基于全局Voronoi图的NNI算法保持一致。

|
| 图 5 基于不同NNI算法的等深线对比图 Fig. 5 Comparison chart of bathymetric contour based on different NNI algorithm |

|
| 图 6 基于不同NNI算法的海底地形表面对比图 Fig. 6 Comparison Chart of marine topography surface based on different NNI algorithm |
此外,为验证基于局部动态最优Voronoi图的NNI算法在精度保持上的优势,借助Surfer8.0软件的残差分析功能,对3组试验结果进行了量化分析,试验结果见表 1。
| Grid-DDM | 试验1 | 试验2 | 试验3 | |
| 残差统计 | 和 | 93.27 | 15.21 | 15.21 |
| 最小值 | -9.89 | -8.01 | -8.01 | |
| 最大值 | 6.48 | 5.89 | 5.89 | |
| 平均值 | 0.007 3 | 0.001 2 | 0.001 2 | |
| 标准方差 | 1.08 | 0.78 | 0.78 | |
| 运行时间/s | 2.13 | 19.45 | 6.72 | |
由表 1中的试验结果可以看出,试验1(基于局部动态Voronoi图的NNI算法)的算法执行效率较高,但算法的插值精度相对较低;试验2(基于全局Voronoi图的NNI算法)与试验1的结论相反,尽管算法的执行效率较低,但算法的插值精度则较高;试验3(基于局部动态最优Voronoi图的NNI算法)则综合了前两种算法的优点,在保证算法插值精度(与试验2的各残差统计项保持一致,均优于试验1)的同时,提高了算法的执行效率(相对于试验2)。
5 结束语本文从NNI算法的构建原理出发,从理论上分析了自然邻点集对NNI算法插值精度的影响。在此基础上,依据Voronoi单胞和Delaunay三角形的几何特性,提出了局部动态最优Voronoi图的概念,并将其应用于NNI中,较好地解决了传统NNI算法存在的插值效率低和精度不高的问题。但需要指出的是,由于在空间索引数据建模和局部离散点集初始化的过程中,所涉及的索引格网行宽、列宽及初始离散点数等参数均采用的是经验参数,理论性和通用性不强,需要进一步研究如何根据离散点集数据量的不同进行自适应估计的问题。另外,为了使得构建的局部动态最优Voronoi图能更好地反映复杂的海底地形,还必须研究离散点集与约束数据集(如与海底地形相关的岸线和等深线数据)的融合问题。
| [1] | SMITH S. The Navigation Surface: A Multipurpose Bathymetric Database[D]. Durham: University of New Hampshire, 2003. |
| [2] | HU Jinxing, MA Zhaoting, WU Huanping, et al. Massive Data Delaunay Triangulation Based on Grid Partition Method[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33 (2): 163-167. (胡金星, 马照亭, 吴焕萍, 等. 基于格网划分的海量数据Delaunay三角剖分[J]. 测绘学报, 2004, 33 (2): 163-167.) |
| [3] | BRAUN J, SAMBRIDGE M. A Numerical Method for Solving Partial Differential Equations on Highly Irregular Evolving Grids[J]. Nature, 1995, 376: 655-660. |
| [4] | LIU Xuejun, ZHANG Ping, ZHU Ying. Suitable Window Size of Terrain Parameters Derived from Grid-based DEM[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38 (3): 264-271. (刘学军, 张平, 朱莹. DEM坡度计算的适宜窗口分析[J]. 测绘学报, 2009, 38 (3): 264-271.) |
| [5] | SUKUMAR N, MORAN B, BELYTSCHKO T. The Natural Element Method in Solid Mechanics[J]. International Journal for Numerical Methods in Engineering, 1998, 43: 839-887. |
| [6] | GAO Yang, ZHANG Jian. Data Interpolation Research Based on the Natural Neighbor Method[J]. Journal of the Graduate School of the Chinese Academy of Sciences, 2005, 22 (3): 346-351. (高洋, 张健. 基于自然邻点插值的数据处理方法[J]. 中国科学院研究生院学报, 2005, 22(3): 346-351.) |
| [7] | CAI Yongchang, ZHU Hehua, WANG Jianhua. The Meshless Local Petrov-Galerkin Method Based on the Voronoi Cells[J]. Acta Mechanica Sinica, 2003, 35 (2): 187-193. (蔡永昌, 朱合华, 王建华. 基于Voronoi结构的无网格局部Petrov-Galekin方法[J]. 力学学报, 2003, 35 (2): 187-193.) |
| [8] | WU Xiaobo, WANG Shixin, XIAO Chunsheng. A New Study of Delaunay Triangulation Creation[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28 (1): 28-35. (武晓波, 王世新, 肖春生. Delaunay三角网的生成算法研究[J]. 测绘学报, 1999, 28 (1): 28-35.) |
| [9] | YU Tiantang REN Qingwen. Natural Neighbor Interpolation and Its Application in Formation of Seepage Field/Initial Stress Field[J]. Metal Mine, 2006, 359 (5): 49-52. (余天堂, 任青文. 自然邻点插值在渗流场/应力场构造中的应用[J]. 金属矿山, 2006, 359 (5): 49-52.) |
| [10] | HU Peng, YOU Lian, YANG Chuanyong, et al. Map Algebra[M]. Wuhan: Wuhan University Press, 2002. (胡鹏, 游连, 杨传勇, 等. 地图代数[M]. 武汉: 武汉大学出版社, 2002.) |
| [11] | CHEN Jun, ZHAO Renliang, QIAO Chaofei. Voronoi Diagram Based GIS Spatial Analysis[J]. Geomatics and Information Science of Wuhan University, 2003, 28 (5): 32-37. (陈军, 赵仁亮, 乔朝飞. 基于Voronoi图的GIS空间分析研究[J]. 武汉大学学报: 信息科学版, 2003, 28 (5): 32-37.) |
| [12] | ZHU Huaiqiu, WU Jianghang. A Vornori Cells Based C∞ Interpolation Basis Function and Its Application in CFD[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2001, 37 (5): 669-678. (朱怀球, 吴江航. 一种基于Voronoi Cells的C∞插值基函数及其在计算流体力学中的若干应用[J]. 北京大学学报: 自然科学版, 2001, 37(5): 669-678.) |
| [13] | TONG Xiaochong, BEN Jin, QIN Zhiyuan, et al. The Subdivision of Partial Grid Based on Discrete Global Grid Systems[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38 (6): 506-513.(童晓冲, 贲进, 秦志远, 等. 基于全球离散网格框架的局部网格划分[J]. 测绘学报, 2009, 38 (6): 506-513.) |
| [14] | TIAN Fengmin, XU Dingjie, ZHAO Yuxin. An Interpolation Method for Constructing Undersea Grid-DEM[J]. Navigation of China, 2009, 32 (3): 61-65.(田峰敏, 徐定杰, 赵玉新. 一种建立海底格网数字高程模型的插值方法[J]. 中国航海, 2009, 32 (3): 61-65.) |
| [15] | ZHU Weining, MA Jingsong, HUANG Xingyuan, et al. A Study of GIS Spatial Competition Analysis Model Based on Projective Weighted Voronoi Diagrams[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33 (2): 146-150. (朱渭宁, 马劲松, 黄杏元, 等. 基于投影加权Voronoi图的GIS空间竞争分析模型研究[J]. 测绘学报, 2004, 33 (2): 146-150.) |
| [16] | GUO Yanjun, PAN Mao, YAN Fei, et al. Application of Natural Neighbor Interpolation Method in Three-dimensional Geological Modeling[J]. Journal of PLA University of Science and Technology: Natural Science Edition, 2009, 10 (6): 650-655. (郭艳军, 潘懋, 燕飞, 等. 自然邻点插值方法在三维地质建模中的应用[J]. 解放军理工大学学报: 自然科学版, 2009, 10 (6): 650-655.) |
| [17] | LIU Jinyi, LIU Shuang. A Survey on Applications of Voronoi Diagrams[J]. Journal of Engineering Graphics, 2004, 22 (2): 125-132. (刘金义, 刘 爽. Voronoi图应用综述[J]. 工程图学学报, 2004, 22 (2): 125-132.) |
| [18] | XIE Shunping, FENG Xuezhi, LU Wei. Algorithm for Constructing Voronoi Area Diagram Based on Road Network Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39 (1): 88-94. (谢顺平, 冯学智, 鲁伟. 基于道路网络分析的Voronoi面域图构建算法[J]. 测绘学报, 2010, 39 (1): 88-94.) |
| [19] | RUI Yikang, WANG Jiechen. A New Study of Compound Algorithm Based on Sweepline and Divide-and-conquer Algorithms for Constructing Delaunay Triangulation[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36 (3): 358-362. (芮一康, 王结臣. Delaunay三角形构网的分治扫描线算法[J]. 测绘学报, 2007, 36 (3): 358-362.) |
| [20] | JIA Juntao, ZHAI Jingsheng, MENG Chanyuan, et al. Construction and Visualization of Submarine DEM Based on Large Number of Multibeam Data[J]. Journal of Geomatics Science and Technology, 2008, 25(4): 255-259. (贾俊涛, 翟京生, 孟婵媛, 等. 基于海量多波束数据的海底地形模型的构建与可视化[J]. 测绘科学技术学报, 2008, 25(4): 255-259. ) |
| [21] | CHEN Jun. Voronoi Dynamaic Spatial Data Model[M]. Beijing: Surveying and Mapping Press, 2002. (陈军. Voronoi动态空间数据模型[M]. 北京: 测绘出版社, 2002.) |
| [22] | ZHU Changqing, SHI Wenzhong. Spatial Analysis Modeling and Theory[M]. Beijing: Science Press, 2006. (朱长青, 史文中. 空间分析建模与原理[M]. 北京: 科学出版社, 2006.) |