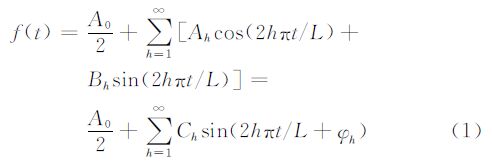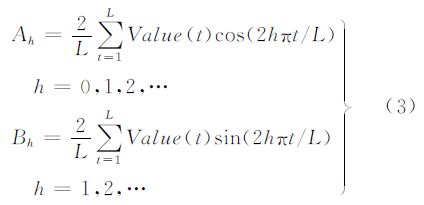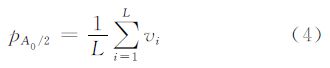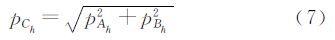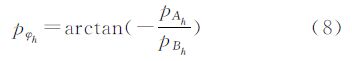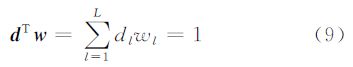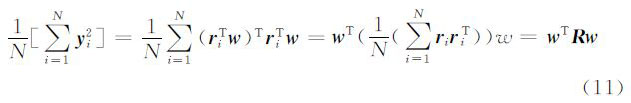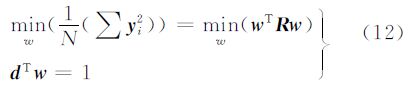2. 南京大学 地理信息科学系,江苏 南京 210093
2. Department of Geographical Information Sciences, Nanjing University, Nanjing 210093, China
高光谱遥感影像目标探测是高光谱遥感应用的重要研究内容之一,其应用领域包括环境监测、城市调查、矿物填图和军事侦察等方面。高光谱遥感的巨大内涵和独特之处在于它可以从数据的高维空间特性入手,基于地物本身的物理属性,进行更有效的目标探测和分类处理。基于此,近年来发展了很多目标探测算法。在目标和背景光谱已知的情况下,文献[1]提出了正交子空间投影(orthogonal subspace projection,OSP)算法,同时考虑了背景光谱和各种噪声下的最大化剩余信号。但很多时候背景光谱并不可知,针对这一情况,文献[1]还提出了一种约束能量最小化(constrained energy minimization,CEM)算法,该算法根据目标光谱,放大特定方向信号,缩小其他背景信号,从而实现目标探测,适用于小目标探测。但CEM探测器难以将目标端元信号与噪声信号分离[2],换言之,CEM假设背景信息中不包含目标,从而得到协方差矩阵Σ。为了解决这一问题,文献[3]提出了一种自适应匹配滤波算法(adaptive matched filter,AMF),该算法用多维正态分布模型模拟背景,但不能很好地表达背景的变化情况。文献[4]分析了椭圆轮廓分布模型探测器(elliptically contoured distributions,ECD),认为该模型能够敏感的预测信号随环境的变化,从而得到了更符合实际情况的背景描述。同时,CEM目标探测的结果往往易受光谱变化的影响。为了降低这种影响,文献[5]首先利用主成分分析(principal component analysis,PCA)技术扣除了图像背景信息,之后借助迭代误差分析(iterative error analysis,IEA)方法选取端元,以端元光谱作为已知光谱代入CEM,从而很好地提取小目标。为了扩展CEM在大目标探测方面的应用,文献[6]也通过设计加权自相关矩阵改进了原算子,提出了一种加权自相关矩阵的CEM算子(weighted correlation matrix CEM,WCM-CEM)。文献[7]研究了正交子空间和目标子空间投影的高光谱数据背景和噪声抑制方法,构造出具有恒虚警特性的检测算法,但是该算法时间复杂度较高,同时算法并不一定具有严格的恒虚警率。文献[8]借助于实码遗传优化投影寻踪方法,从分布异常的角度,提出了一种非监督特征投影方法提取小目标,但该算法因为依据分布异常理论发现小目标,因此具有一定的盲目性。前述OSP、CEM、AMF、ECD 、PCA-IEA-CEM以及WCM-CEM等算法均假定目标光谱已知,而在目标和背景光谱均未知的情况下,文献[9]发展了异常探测算子RXD,其算法依赖于异常目标往往游离于图像数据所构造的数据“云团”超平面之外这一假设,即当图像在异常像元与图像均值向量的连线方向上的投影有较大方差时,该算子失效[6]。为解决RXD探测失效的问题,文献[10, 11]设计了一种基于数据白化距离的异常探测(whited-distance abnormity anomaly detection,WAAD)算法,该算法对高光谱数据进行白化处理,使数据“云团”在特征空间中呈球状分布,而异常像元仍处于球状云团之外。文献[12]提出了基于前若干个最佳小波包基特征参量数组的目标识别方法,该方法可同时保留目标高低频信息,并可自动消除数据异常,从而降低了数据维数。然而,目前基于谐波分析(harmonic analysis,HA)的高光谱影像目标探测技术研究还甚少。本文将从高光谱维谐波分析的角度来探索性研究与试验高光谱影像的小目标探测与识别技术。所谓小目标,有学者认为[11, 13, 14]:在物性上它明显区别于影像中的背景地物,而且有着特殊的光谱特征,常表现为区域上的异常;在几何上它又往往分布在具有单形体结构的数据云团的顶点上;在信息量上,小目标通常只占几个至几十个像元,甚至是亚像元。这些也构成小目标探测的理论基础。
谐波分析技术广泛应用于电力污染检测和去除等,如文献[15]基于BP神经网络检测电力系统谐波,给出了3次谐波的训练和仿真,可用于电力系统的实时检测和谐波动态补偿。在遥感领域,目前谐波分析多用于分析时间序列数据,最初由文献[16, 17]提出,并利用谐波分析技术对26个阶段的年内AVHRR NDVI 时间序列进行分析,以描述自然和农业土地利用的季节性变化,同时也研究了谐波分析在农作物物种识别中的应用,并在堪萨斯州南部进行了试验;文献[18]针对MODIS时间序列数据,利用谐波分析手段探测作物物候现象;文献[19]基于谐波分析方法探索了一种曲线拟合技术,从带噪声的NDVI时间序列数据中提取出年内物候规律。针对高光谱影像目标探测问题,目前尚无文献可查。本文基于AVIRIS(机载可见光/近红外成像光谱仪)高光谱影像数据,结合白化处理(whitening processing,WP)和约束能量最小化(CEM)算法,提出一种基于谐波分析的小目标探测新模型(HA-WP-CEM)。该模型首先采用谐波分析提取高光谱遥感数据的谐波余项、谐波振幅、谐波相位等表征能量谱的特征成分,然后对获取的各能量谱特征成分进行白化处理,实现抑制背景信息和突出小目标信息,因此也可以有效去除数据噪声。最后利用CEM算子进行小目标探测。同时采用CEM、WP-CEM、结合PCA的CEM(PCA-CEM)与PCA-WP-CEM等方法进行影像目标探测,进而综合分析与评价HA-WP-CEM模型探测结果的可靠性及准确性。
2 理论与方法 2.1 高光谱遥感数据的谐波分析文献[20, 21]认为:以正(余)弦波(谐波)相叠加的形式来表示时间序列f(t)的方法称为谐波分析(HA)。它把时间序列数据从时域变换到频率域,并寻找变换参量,在频域空间中以多个频率不同的正(余)弦曲线叠加表示时域分量。
一般情况,任何周期波形都可以展开为式(1)所示的傅里叶级数形式[22],即
式中 式(1)、式(2)中,t表示时间;A0/2表示谐波余项;L表示周期;h表示谐波分析次数;C1sin(2π/L+φ1)表示基波分量;Chsin(2hπ/L+φh)表示第h次谐波分量;φh表示第h次谐波的初相位;Ch表示振幅;C2h表示功率谱。在应用于高光谱数据方面,传统的傅里叶分析是将每一个波段的影像从空间域变换到频率域,其所采用的是二维傅里叶变换,变换后的影像由所有波段的频率域图像组成,反映了每个波段影像上像元灰度值的变化剧烈程度。这种处理技术并没有真正利用数据的高光谱维进行分析,仅仅是对每一维的数据单独分析,没有提取分析不同维的数据关系或特征。鉴于此,本文将研究一种基于高光谱数据的HA技术,该技术从高光谱维入手,设计了适于高光谱数据的傅里叶变换新模型,如式(1)~(3)所示。通过分析提取不同光谱维之间的特征,在保持高光谱数据空间特性不变的情况下,从光谱维层面把高光谱数据变换成由谐波特征成分组成一组分量。具体到单个像元而言,在保持像元空间位置特性的基础上,它将每个像元光谱数据表达为一系列由振幅和相位确定的正(余)弦波加性项的和,这样单像元光谱便以一条复杂而平滑的曲线来表示。其变换的物理意义是:反映了像元在各个波段的能量均值、不同波段的能量变化以及能量出现幅值的波段位置。
对于离散高光谱像元矢量数据,记为Value(t),其谐波展开式同式(1),而对于Ah、Bh,可采用式(3)计算。
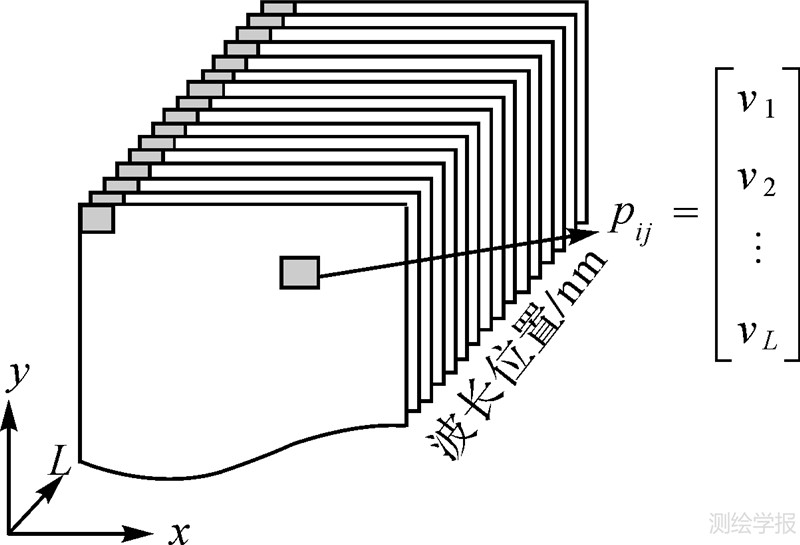
式中,t在此处表示波段号数;L表示波段总数,其他符号同式(1)。高光谱影像的谐波分析以离散像元为处理单元,下面以单个像元点的变换过程简述其原理。假设pij为高光谱影像上第i列第j行的某像元,其光谱矢量为[v1 v2 … vL]T,则其h次谐波变换的具体变换过程如下:
(1)计算p点谐波余项pA0/2
(2)计算p点pAh、pBh(3)计算p点谐波振幅pCh
(4)计算p点谐波初始相位pφh
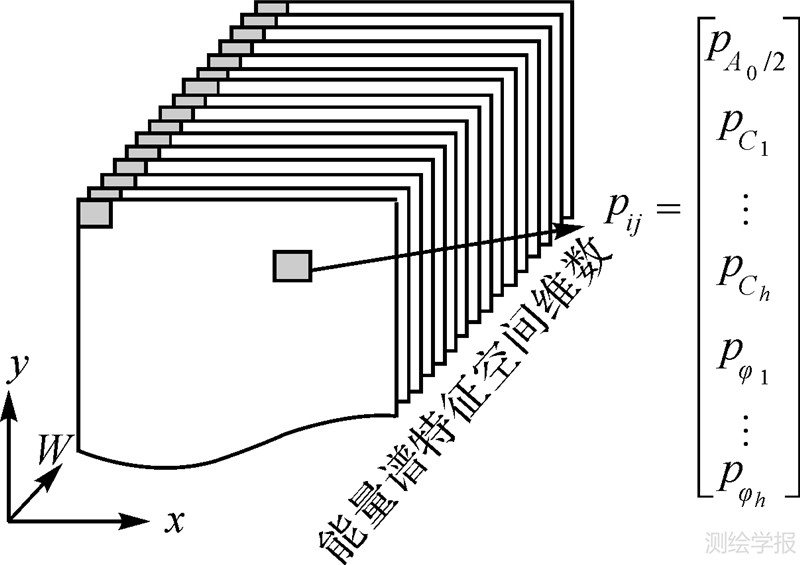
图 1和图 2分别显示了HA变换前后的光谱维空间。其中变换后的能量谱特征空间维数(W)为W=2h+1。
|
| 图 1 光谱维矢量空间 Fig. 1 Spectral dimentional vector space |
|
| 图 2 能量谱的特征成分空间 Fig. 2 Feature components space of the HA energy spectra |
2.2.1 CEM算法思想
约束能量最小化(CEM)算法是在参考光谱已知、背景光谱未知的条件下对小目标进行探测和提取的算法[6]。算法根据目标光谱,放大特定方向信号,衰减其他背景信号,从而实现目标提取。其具体思想如下:
记S={r1,r2,…,rN}为所有高光谱数据像元矢量集合,其中ri=[ri1 ri2 … riL]T为任意像元光谱矢量,i=1,2,…,N,N为像元数目,L为影像波段总数。假设d=[d1 d2 … dL]T为已知目标像元光谱矢量,CEM就是要设计这样一种线性滤波器w=[w1 w2 … wL]T,使之满足
当输入像元光谱矢量ri时,经过滤波器,其输出yi为
所有像元光谱输入滤波器后,平均输出能量为
式中,R=( ∑rirTi)/N是影像数据集S的自相关矩阵。滤波器w的设计就是求式(11)在约束条件式(9)下的最小值问题,即
2.2.2 CEM算子的求解采用拉格朗日乘数法对该约束条件最小值问题进行求解,求解步骤如下:
(1) 构造拉格朗日函数
(2) 求偏导
(3) 令偏导等于0,得
(4) 将w代入式(9),得
(5) 将λ代入步骤(3),得算子为
在影像上,小目标往往表现为低概率分布,与影像背景相比较,其信息量很微小,若要从这些大量信息中提取出所需要的微量信息,必须对图像背景作抑制处理。白化处理使影像数据各波段方差为1,波段间信息相关性为0,很好地缩减图像信息量大的方向,放大信息量较小的方向。这使得低概率目标(小目标)游离于图像背景的数据“云团”之外,从而使小目标探测变得相对容易。WP的具体算法如下[23]:
(1)计算S的均值向量μ

(2)计算S的协方差矩阵K
(3)求白化矩阵F,使
经计算,F=EΔ-1/2,E由K的特征向量组成,且ETKE =Δ。那么,将F作用于S,得白化数据S*为
试验数据为美国加州圣地亚哥北部岛屿某海军飞机场的AVIRIS高光谱影像数据,如图 3所示。该区域类似于一个小型城市,具有自己的安保、消防、公园、海滩、居民区和休憩场所等,还包括一个军用仓库。该数据光谱范围是0.4~1.8 μm,像元分辨率为3.5 m,共有137个波段,有效波段131个。试验区域中飞机为探测目标,其中极少量飞机可以目视探测,大部分飞机无法人工识别,如图 3中“large target”可从形状上识别为大型飞机。

|
| 图 3 AVIRIS高光谱影像 Fig. 3 AVIRIS hyperspectral imagery |
以试验区AVIRIS高光谱影像像元点为计算单元,取h=0,L=137,根据式(3)计算谐波余项A0/2;取h=1、2、3,L=137,根据式(2)、式(3)计算影像谐波分析的1~3次谐波振幅C1~C3和谐波相位φ1~φ3。相应的谐波余项A0/2、谐波振幅与谐波相位能量谱特征成分如图 4所示。通过多层次的谐波分析可以看出前3个谐波振幅(C1~C3)包含了波谱能量的主要成分(如图 4),而且消除了部分噪声,同时剔除了异常点。

|
| 图 4 谐波分析的各能量谱特征成分影像 Fig. 4 Energy spectral feature components of the harmonic analysis |
在进行CEM处理时,对各能量谱特征成分进行统一的坐标配准校正并编号,见表 1,地图投影采用UTM,椭球基准面选择North America 1927。重采样采用最近邻插值法,数据像元大小为1 m。特征成分HA_1、HA_2和HA_5的RGB合成图像如图 5所示。
| m | ||
| 特征成分号 | 谐波分析特征成分 | 像元大小 |
| HA_1 | A0/2 | 1 |
| HA_2 | C1 | 1 |
| HA_3 | C2 | 1 |
| HA_4 | C3 | 1 |
| HA_5 | φ1 | 1 |
| HA_6 | φ2 | 1 |
| HA_7 | φ3 | 1 |

|
| 图 5 谐波分析成分的假彩色合成影像 Fig. 5 A false color compositing image of the HA components |
对谐波分析特征成分白化处理后,HA_1、HA_2和HA_5的RGB合成图像如图 6所示,其计算得出的白化矩阵F如表 2所示。

|
| 图 6 白化处理成分的假彩色合成影像 Fig. 6 A false color compositing image of the WP components |
| 7×7 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 4.1E+01 | 4.2E-01 | -2.9E+00 | -1.9E+02 | 2.8E+01 | 5.4E+01 | -8.9E+01 |
| 2 | -3.5E+02 | 1.2E+02 | -1.2E+01 | -2.9E+01 | 2.1E+02 | -2.5E+02 | -1.5E+01 |
| 3 | 6.6E+01 | -3.3E+02 | 1.0E+01 | -1.7E+03 | -4.5E+02 | -8.0E+01 | -5.7E+00 |
| 4 | -3.3E+00 | 7.4E+01 | -6.6E+01 | 2.5E+03 | -3.0E+02 | -5.2E+01 | -1.1E+01 |
| 5 | -1.2E+04 | 2.6E+04 | 1.0E+05 | 7.7E-01 | -3.1E-01 | -2.2E-02 | -8.9E-03 |
| 6 | 1.6E+04 | 1.5E+05 | -1.8E+04 | -5.0E+00 | -9.4E-01 | 3.4E-02 | 6.8E-03 |
| 7 | 2.3E+05 | -8.7E+03 | 6.7E+03 | 8.8E-01 | 4.9E-01 | -3.7E-01 | -7.1E-03 |
根据图 3和白化处理数据S*,在图 6中提取大目标(飞机)像元的光谱矢量数据,共33个(图 3左上角3个大飞机的17个像元矢量,中间3个大飞机的16个像元矢量),计算其均值向量d均=[0.018 8,-1.241,-1.071,-1.524 5,0.516 3,0.113 1,-1.677 7]T,作为CEM探测算子的目标参考矢量。
3.6 基于HA-WP-CEM模型的小目标探测根据S*,计算其自相关矩阵R*,将R*和d均代入CEM算子w*,并将w*作用于S*,最终得到小目标探测结果,如图 7所示,其自相关矩阵R*如表 3所示。从图 7中可以看出,机场中所有大、小飞机均探测到。

|
| 图 7 小目标的探测结果 Fig. 7 The detection results of small targets |
| 7×7 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 2.744 | -1.594 | 0.945 | 1.260 | 1.681 | 0.043 | 2.872 |
| 2 | -1.594 | 2.457 | -0.863 | -1.151 | -1.536 | -0.039 | -2.625 |
| 3 | 0.945 | -0.863 | 1.512 | 0.682 | 0.910 | 0.023 | 1.556 |
| 4 | 1.260 | -1.151 | 0.682 | 1.910 | 1.214 | 0.031 | 2.075 |
| 5 | 1.681 | -1.536 | 0.910 | 1.214 | 2.620 | 0.041 | 2.768 |
| 6 | 0.043 | -0.039 | 0.023 | 0.031 | 0.041 | 1.001 | 0.070 |
| 7 | 2.872 | -2.625 | 1.556 | 2.075 | 2.768 | 0.070 | 5.731 |
为了检查基于HA-WP-CEM模型的小目标探测结果的可靠性,本文引用了该研究区域的高空间分辨率遥感影像(图 8)进行探测信息比对,验证发现探测效果较好,如图 9所示。

|
| 图 8 研究区域的高空间分辨遥感影像 Fig. 8 The high-spatial resolution image of the study area |

|
| 图 9 基于高空间分辨遥感影像的探测结果验证 Fig. 9 The verification of the results by a high-spatial resolution image |
为了说明HA-WP-CEM模型的探测优势与性能,对本方法与CEM、WP-CEM、PCA-CEM、PCA-WP-CEM 4种方法作了探测结果对比分析。该4种方法与本文HA-WP-CEM模型的探测结果如图 10所示。

|
| 图 10 不同方法的探测结果 Fig. 10 The target detection results of different methods |
从图 10中可以看出,由于没有进行背景抑制,对原始影像直接进行CEM的目标探测效果较差(如图 10(a));直接对原始影像进行白化处理,同时目标信息也受到抑制,之后用CEM探测效果很差(如图 10(b));PCA-CEM技术虽然先进行了数据主成分提取(此处选择了PCA变换后的前10个分量),但由于没有作背景抑制,探测效果稍差(如图 10(c));对原始数据提取主成分后,提取了主成分信息图像,消除了大部分噪声,之后进行白化处理,很好地抑制了背景,再进行CEM探测,整体效果虽然较好,但出现了信息丢失的现象,如左下角机场部分小飞机和中间机场的其中一架大飞机都没有探测到(如图 10(d));本文提出的HA-WP-CEM探测模型首先采用了反映数据能量谱信息的谐波分析特征成分来进行后续处理,一方面达到了数据变换的目的,同时使特征成分数据尽可能完整地反映数据信息(进行了3次谐波分析),其中谐波相位成分反映了数据最大能量的波段位置,最为敏感,之后利用白化处理抑制背景,再利用CEM探测目标后,机场中大、小目标飞机均被探测到,效果最佳(如图 10(e))。
4.2 定量评价将影像上存在的几个小型停机场分别命名为Airport-1(左上角)、Airport-2(中部)、Airport-3(左下部)。通过对比高分辨影像计算不同探测结果的信噪比(signal to noise ratio,SNR)、探测率(correct detection ratio,CDR)、漏检率(missed detection ratio,MDR)和虚警率(false alarm ratio,FAR),3个机场的定量评价结果如表 4~6所示,不同探测方法的综合定量评价结果如表 7所示。
| Airport1 | CEM | WP-CEM | PCA-CEM | PCA-WP-CEM | HA-WP-CEM |
 | |||||
| SNR | 10.99 | 9.36 | 13.91 | 18.27 | 31.85 |
| CDR/(100%) | 1 | 0 | 0 | 1 | 1 |
| MDR/(100%) | 0 | 1 | 1 | 0 | 0 |
| FAR/(100%) | 0 | 0 | 0 | 0.4 | 0 |
| Airport2 | CEM | WP-CEM | PCA-CEM | PCA-WP-CEM | HA-WP-CEM |
 | |||||
| SNR | 15.60 | 12.84 | 19.55 | 27.65 | 32.56 |
| CDR/(100%) | 0.67 | 0 | 0 | 1 | 1 |
| MDR/(100%) | 0.33 | 1 | 1 | 0 | 0 |
| FAR/(100%) | 0 | 0 | 0 | 0 | 0 |
| Airport3 | CEM | WP-CEM | PCA-CEM | PCA-WP-CEM | HA-WP-CEM |
 | |||||
| SNR | 4.57 | 5.19 | 11.01 | 8.45 | 33.70 |
| CDR/(100%) | 0 | 0 | 0 | 0.2 | 0.97 |
| MDR/(100%) | 1 | 1 | 1 | 0.8 | 0.03 |
| FAR/(100%) | 1 | 0 | 0 | 0 | 0.1 |
| Average | CEM | WP-CEM | PCA-CEM | PCA-WP-CEM | HA-WP-CEM |
| SNR | 10.39 | 9.13 | 14.82 | 18.12 | 32.70 |
| CDR/(100%) | 0.56 | 0 | 0 | 0.73 | 0.99 |
| MDR/(100%) | 0.44 | 1 | 1 | 0.27 | 0.01 |
| FAR/(100%) | 0.3 | 1 | 1 | 0.13 | 0.03 |
根据表 4~7可以看出: HA-WP-CEM信噪比最大,达到32.7,目标探测正确率达到99%,目标漏检率仅为1%,虚警率也仅为3%,其他4种方法均低于这一水平。但是,PCA-WP-CEM探测水平接近于HA-WP-CEM,其信噪比为18.12,目标探测正确率为73%,目标漏检率为27%,虚警率过高,达到了13%。
4.3 分析总结通过定性和定量分析对比5种探测技术可以发现,PCA-WP-CEM和HA-WP-CEM探测效果接近,但是后者的探测效果更为明显,目标基本游离于影像背景特征空间之外,而且被测目标基本无遗漏。剖析其原理:PCA是通过影像的自相关矩阵或协方差矩阵,构建正交线性变换矩阵,将影像变换到各主成份空间中,且最大特征值对应于影像的第一主成份。PCA仅仅考虑了波段之间的关系,并以这种关系构建变换参数。而本文提出的HA技术不仅考虑了波段之间的关系,而且着重从不同波段波形变换的角度提取信息,其提取出的振幅和相位信息对小目标等影像的异常信息非常敏感,故其探测效果非常好,在高光谱影像小目标探测领域有可借鉴之处。
5 结 论本文结合白化处理与CEM算子,提出了一种基于谐波分析的HA-WP-CEM高光谱遥感影像小目标探测模型。通过试验与对比分析,得出如下结论:
(1) 利用谐波分析手段,对原始高光谱数据进行频率域能量谱主信息分解,能达到数据变换的目的,也在一定程度上进行了数据降噪,而且在目标探测方面比常规的PCA变换技术更加有效,可以预见HA在高光谱数据变换、特征提取、分类预处理等方面的应用。
(2) 经白化处理后可以很好地抑制背景信息,再进行CEM的目标探测比直接进行目标探测效果好。
(3) 直接利用CEM时,影像自相关矩阵R易出现奇异的情况,很难精确地计算出R-1,导致探测结果不准确。
(4) 原始高光谱影像直接作白化处理时计算量异常大,如本研究采用的数据波段为137,则白化矩阵F大小为137×137,而矩阵S的大小为162 000×137,随之FTS的计算量会成倍增大,因此,该算法直接应用于原始影像,其整体计算量之大可见一斑。
综上所述,在高光谱遥感数据目标探测方面,本文提出的HA-WP-CEM模型与常规的CEM、WP-CEM、PCA-CEM、PCA-WP-CEM探测方法相比,在实现的简易性、可靠性、实用性和准确性方面表现出了明显的优势。
| [1] | HARSANYI J C. Detection and Classification of Sub-pixel Spectral Signatures in Hyperspectral Image Sequences[D]. Baltimore: University of Maryland, 1993. |
| [2] | DU bo. Sub-pixel Target Detection from Hyperspectral Remote Sensing Imagery[D]. Wuhan: Wuhan University, 2010: 1-152. (杜博. 高光谱遥感影像亚像元小目标探测研究[D]. 武汉: 武汉大学, 2010: 1-152.) |
| [3] | ROBEY F C, FUHRMANM D R, KELLY E J, et al. A CFAR Adaptive Matched Filter Detector[J]. IEEE Transactions on Aerospace and Electronic Systems, 1992, 28(1): 208-216. |
| [4] | LIU Xiang. Target Detection on Hyperspectral Imagery Based on Transformation of Spectral Dimensions[D]. Beijing: Institute of Remote Sensing Applications of CAS, 2008: 1-182. (刘翔. 基于光谱维变换的高光谱图像目标探测研究[D]. 北京: 中国科学院遥感应用研究所, 2008: 1-182.) |
| [5] | XUN Lina, FANG Yonghua, LI Xin. Target Detection Algorithm in Hperspectral Image Based on CEM[J]. Opto-Electronic Engineering, 2007, 34(7): 18-21. (寻丽娜, 方勇华, 李新. 基于CEM的高光谱图像小目标检测算法[J]. 光电工程, 2007, 34(7): 18-21.) |
| [6] | ZHANG Bing, GAO Lianru. Hyperspectral Image Classification and Target Detection[M]. Beijing: Science Press, 2011: 223-226. (张兵, 高连如. 高光谱图像分类与目标探测[M]. 北京: 科学出版社, 2011: 223-226.) |
| [7] | HE Lin, PAN Quan, ZHAO Yongqiang, et al. CFAR Target Detection in Unknown Background Based on Subspace Projection in Aerial Hyperspectral Imagery[J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(4): 657-662. (贺霖, 潘泉, 赵永强, 等. 基于空间子投影的未知背景航拍高光谱图像恒虚警目标检测[J]. 航空学报, 2006, 27(4): 657-662.) |
| [8] | LU Wei, YU Xuchu, LIU Juan, et al. A Small Targets Detection Approach Based on Anomaly Distributing in Hyperspectral Imegery[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(1): 40-45. (路威, 余旭初, 刘娟, 等. 基于分布异常的高光谱遥感影像小目标检测算法[J]. 测绘学报, 2006, 35(1): 40-45.) |
| [9] | REED I S, YU X. Adaptive Multiple-band CFAR Detection of an Optical Pattern with Unknown Spectral Distribution[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1990, 38(10): 1760-1770. |
| [10] | GENG Xiurui. Target Detection and Classification for Hyperspectral Imagery[D]. Beijing: Institute of Remote Sensing Applications of CAS, 2005: 1-104. (耿修瑞. 高光谱遥感图像目标探测与分类技术研究[D]. 北京: 中国科学院遥感应用研究所, 2005: 1-104.) |
| [11] | GENG Xiurui, ZHAO Yongchao. Basic Theory of Small Target Detecting of Hyperspectral Remote Sensing Imagery[J]. Science in China: Series D, Earth Science, 2007, 37(8): 1081-1087. (耿修瑞, 赵永超. 高光谱遥感图像小目标探测的基本原理[J]. 中国科学: D辑, 地球科学, 2007, 37(8): 1081-1087.) |
| [12] | YANG Keming, LI Hui, GUO Dazhi. Feature Mapping of Hyperspectral Images Based on Best Basis of Wavelet Packet Decomposition[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1): 54-58. (杨可明, 李慧, 郭达志. 基于最佳小波包基的高光谱影像特征制图[J]. 测绘学报, 2008, 37(1): 54-58.) |
| [13] | LI Qingbo, LI Xiang, ZHANG Guangjun. A Hyperspectral Small Target Detection Method Based on Outlier Detection[J]. Spectroscopy and Spectral Analysis, 2008, 28(8): 1832-1836. (李庆波, 李响, 张广军. 一种基于光谱奇异值检测的高光谱遥感小目标探测方法[J]. 光谱学与光谱分析, 2008, 28(8): 1832-1836.) |
| [14] | CHANG C I, CHIANG S S. Anomaly Detection and Classification for Hyperspectral Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(6): 1314-1325. |
| [15] | TANG Shengqing, CHENG Xiaohua. A Harmonic Measuring Approach Based on Multilayered Feed Forward Neural Network[J]. Proceedings of the CSEE, 2006, 26(18): 90-94. (汤胜清, 程小华. 一种基于多层前向神经网络的谐波检测方法[J].中国电机工程学报, 2006, 26(18): 90-94.) |
| [16] | JAKUBAUSKAS M E, LEGATES D R, KASTENS J H. Harmonic Analysis of Time-series AVHRR NDVI Data[J]. Photogrammetric Engineering & Remote Sensing, 2001, 67(4): 461-470. |
| [17] | JAKUBAUSKAS M E, LEGATES D R, KASTENS J H. Crop Identification Using Harmonic Analysis of Time-series AVHRR NDVI Data[J]. Computers and Electronics in Agriculture, 2002, 37(1-3): 127-139. |
| [18] | TOSHIHIRO S, MASAYUKI Y, HITOSHI T, et al. A Crop Phenology Detection Method Using Time-series MODIS Data[J]. Remote Sensing of Environment, 2005, 96(3/4): 366-374. |
| [19] | BETHANY A B, ROBERT W J, JOHN F H, et al. A Curve Fitting Procedure to Derive Inter-annual Phenologies from Time Series of Noisy Satellite NDVI Data[J]. Remote Sensing of Environment, 2007, 106(2): 137-145. |
| [20] | RAYNER J N. An Introduction to Spectral Analysis[M]. London: Pion Ltd, 1971. |
| [21] | DAVIS J C. Statistics and Data Analysis in Geology[M]. 2nd ed. New York: John Wiley & Sons, 1986. |
| [22] | WAKILEH G J. Power Systems Hanrmonics: Fundamentals, Analysis and Filter Design[M]. New York: Springer, 2001. |
| [23] | TONG Qingxi, ZHANG Bing, ZHENG Fenlan. Hyperspectral Remote Sensing: Principles, Technology and Applications[M]. Beijing: Higher Education Press, 2006: 218-238.(童庆禧, 张兵, 郑芬兰. 高光谱遥感:原理、技术与应用[M]. 北京: 高等教育出版社, 2006: 218-238.) |